Simplified Blind Algorithms based on Cross-Information Potential
Copyright ⓒ 2024 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract
The learning algorithm for blind signal processing developed from the performance criterion of cross-information potential (CIP) has superior compensation performance for intersymbol interference induced by channel distortion, even under impulsive noise. One of the drawbacks of the CIP algorithm is a heavy computational complexity caused by considering all the interactions between N (sample size) output samples and the symbol points where a large sample size is preferable to guarantee a desired level of accuracy in distribution estimation. In this paper, the idea of taking only the current output sample into their interactions instead of all output samples is proposed under the assumption that the information the current sample has is the most useful of all other samples; this leads to the computational complexity of the proposed algorithm not being related to the sample size. The simulation results show that the proposed algorithm significantly reduces the computational complexity by approximately 21 times for N=20 without noticeable loss of learning performance, which indicates that the proposed criterion and algorithm are more suitable for practical implementations than the conventional CIP algorithm.
초록
CIP(Cross-Information Potential) 성능 기준을 바탕으로 개발된 블라인드 신호 처리 학습 알고리즘은 충격성 잡음 환경에서도 채널 왜곡으로 인한 심볼 간 간섭에 대한 보상 성능이 뛰어나다. CIP 알고리즘의 단점 중 하나는, 원하는 수준의 확률분포 정확도를 보장하기 위해 N(샘플 사이즈)개의 출력 샘플과 심볼점 간의 모든 상호 작용을 고려하므로 큰 샘플 사이즈가 선호되어 계산 복잡성이 크다는 점이다. 본 논문에서는 다른 모든 샘플보다 현재 샘플이 갖고 있는 정보가 가장 유용하다는 가정하에 모든 출력 샘플 대신 현재 출력 샘플만 상호 작용에 사용하기를 제안하며 이로 인해 제안된 알고리즘의 계산 복잡도가 샘플 크기와 관련이 없게 된다. 시뮬레이션 결과에서 제안한 알고리즘은 N=20에 대해 학습 성능의 큰 손실 없이 계산 복잡도를 약 21배 정도 감소시켰으며, 이는 제안한 성능 기준 및 알고리즘이 기존 CIP 알고리즘보다 실제 구현에 더 적합할 수 있음을 나타낸다.
Keywords:
Cross-Information Potential, Computational Burden, Blind Signal Processing, Simplification, Impulsive Noise키워드:
상호-정보 포텐셜, 계산 복잡성, 블라인드 신호 처리, 단순화, 충격성 잡음Ⅰ. Introduction
Blind algorithms for signal processing or communication systems are being effectively utilized in overcoming signal distortion or inter-symbol interference induced by storage media or communication channels. Blind algorithms do not need a training sequence to recover the distorted signal or to restart after a communications breakdown[1],[2]. This advantage has been increasingly utilized in computer communication networks and broadcasting systems[3].
The training of blind adaptive systems has usually been accomplished by using the constant modulus error (CME) and the mean squared error (MSE) criterion[4],[5]. Unlike the MSE criterion that utilizes CME energy, ITL methods introduced by Princepe uses a nonparametric probability density function (PDF) estimation and information potential (IP) which measures interactions among pairs of data samples[6],[7]. It contains higher order moments of the PDF and is much simpler to estimate directly from samples than conventional moments expansions.
The MSE based learning algorithms are known not to yield sufficient performance in non-Gaussian noise, such as impulsive noise environments[6],[8]. On the other hand, learning algorithms developed from the ITL methods can break through these obstacles partly due to the kernel-based PDF estimation and information potential[6]. The minimum error entropy (MEE) criterion as one of ITL criteria is a powerful approach for non-Gaussian signal processing as well as for robust machine learning[9],[10]. One of its drawbacks is that it has been designed only for supervised learning. Another problem is its computational complexity including double summation operations. Recently a simplified version of MEE has been introduced by utilizing only two error samples that contribute mostly to performance enhancement[11].
Besides the concept of IP, through the extension of the definition of correlation function for random processes, the generalized correlation function called correntropy has become another performance criterion of ITL and developed to be applied to blind signal processing[12]. The correntropy is related to the probability of how similar two random variables are in the neighborhood of the joint space[13].
In this paper, in order to develop efficient and unsupervised learning algorithms which are robust in impulsive noise environment, we briefly explain blind algorithms based on correntropy and IP, and then propose a simplified IP criterion and its related algorithms for computational complexity reduction without noticeable loss of performance.
Ⅱ. Blind Performance Criteria based on Gaussian Kernel
With a kernel size σ, the Gaussian kernel is defined as
| (1) |
Given N(sample size) data samples {xi}, the correntropy function VX [n] with sample distance or time distance n is described as follows[12],[13].
| (2) |
When it comes to dissimilarity measure as a kind of error concept, the squared difference CSY between the transmitter correntropy VS[n] and that of the receiver VY[n] can become a cost function or a performance criterion as proposed in[12]. We refer to this CSY as MSCD (mean squared correntropy distance) in this paper for convenience’s sake.
| (3) |
On the other hand, the information potential (IP) can be a kind of performance criterion. The concept of information potential may be summarized as follows.
When we see the value of a given data sample xi as the location of the data axis x, the kernel function Gσ√2(xj - xi) for two data samples xi and xj on the axis produces exponential decaying outcomes regarding the distance between xi and xj. This can be interpreted as the Gaussian kernel Gσ√2(xj - xi) plays a role as a potential field that induces the interactions between the two particle-like data samples xi and xj. The perspective regarding a data sample as a particle with information in an information potential field becomes the basis of the concept of information theoretic learning (ITL)[6],[7].
Then is corresponding to the summed interactions towards to xi and becomes the averaged total interaction among all data samples on the x axis. This function of total interactions is called information potential[6]. That is, the information potential IPXX for a given set of samples can be written as
| (4) |
We may notice in (4) that when the samples are placed close to each other the potential energy becomes high and vice versa.
The information potential can be expressed with a probability density function fX(x) based on kernel density estimation method[14].
| (5) |
Then, becomes
| (6) |
Therefore,
| (7) |
For the two different densities fS(s) and fY(y), the cross information potential (CIP) called information potential CIPSY is defined in[7] as
| (8) |
We can notice that when the samples si and yi are placed close together the information potential CIPSY becomes high and vice versa.
For application to blind equalization in communication with M-ary modulation schemes, technology, the density fS(s) can be constructed from the transmitter symbol set and density fY(y) is from the receiver output samples . When the transmitted symbol at time k is assumed to be randomly chosen with equal probability, fS(s) and fY(y) can be obtained
| (9) |
where δ(s) is the Dirac-delta function on the s axis.
And through the kernel density estimation method with the sample size N as in (5) fY(y) becomes
| (10) |
Then the equation (8) using (9) and (10) can be rewritten as
| (11) |
The two ITL-type criteria, CSY of MSCD, and CIPSY of CIP can be summarized as in (3) and (11), respectively.
For comparison’s sake, the common blind criterion PCMA for the constant modulus algorithm (CMA) can be rewritten as
| (12) |
- where
Minimizing this criterion leads to force equalizer output powers to have the same value, R2. In M-ary modulation schemes, the power of each desired signal has different values. The force induced from minimizing PCMA will lose its target direction because the cost function forces the equalizer outputs to obtain the same output power R2 in spite of each symbol’s desired power being different from each other. This may lead the CMA cost function R2 to ill-convergence more severely in impulsive noise situations.
Ⅲ. Proposed CIP Criterion
The fact that the information potential IPXX in (2) is the interaction energy among all data samples on the x axis leads us to view the CIP in (11) as the interactions between the M symbol points and N output samples .
Instead of considering all the interactions of N output samples towards to the symbol points, we may consider only that of yk under the assumption that the information the current sample yk has is the most useful of all other samples. This assumption will be verified through experiment in Section V.
So, we intend to consider only the interactions between yk and all symbol points {A1,A2,...,AM}. Then the simplified CIP becomes
| (13) |
This proposed (13) will be referred to as SCIP (simplified CIP) in this paper. It may be needed to observe performance difference between CIPSY and its simplified version SCIPSY through the experiment in Section V.
Ⅳ. Blind Learning Algorithms
For the input vector and weight at time k, the linear combiner produces the output . The MSCD algorithm for weight update is obtained by minimizing CSY in (3) with a step size μMSCD.
| (14) |
The CIP algorithm is obtained by maximizing CIPSY in (11) as
| (15) |
Likewise, maximizing SCIPSY leads to SCIP algorithm with a step size μSCIP as
| (16) |
For comparison, the CMA algorithm (CMA) obtained from minimizing PCMA with respect to system weights can be written as
| (17) |
It may be worthwhile to observe different performance among CMA in (12), MSCD in (3), CIP in (11) and its simplified version SCIP in (13) through the experiment in Section V.
Ⅴ. Simulation Results and Discussion
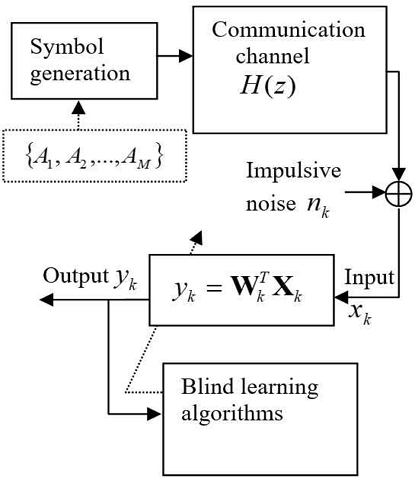
In this Section, the learning performance of the MSCD algorithm and its simplified version SCIP is analyzed in the experiment of a base-band communication system as shown in Fig. 1.
For the data generation of 4 symbols (M = 4), one of is randomly chosen (equiprobable) and sent at time k. The transmitted symbol is through the communication channel H(z) where the symbol is distorted by intersymbol interference and then corrupted by impulsive noise. The receiver is equipped with a linear combiner with L = 11. The transfer function H(z) is in (18) as in[8].
| (18) |
The impulse response of (18) corresponds to
| (19) |
where T is the symbol period.
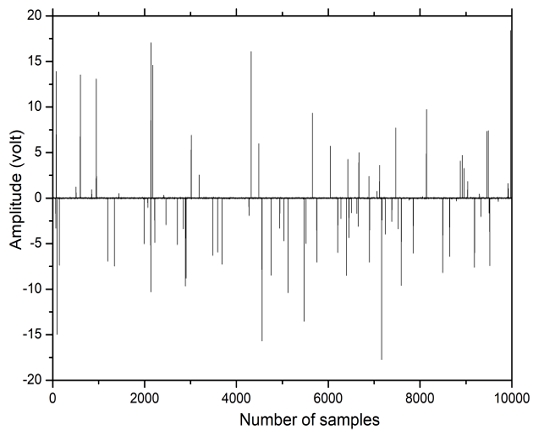
The impulsive noise comprises impulses and white Gaussian noise. The impulses are generated as in[12],[13] by Poisson process with variance 50 and occurrence rate 0.03. The variance of the Gaussian noise is set 0.001. A sample of the impulsive noise is shown in Fig. 2.
The system weights of the CIP and SCIP are updated with the common step size μCIP=μSCIP = 0.005 and the kernel size σ = 0.6. The step sizes for CMA and MSCD, μCMA and μMSCD are set 0.01 and 0.00001, respectively. The kernel size for MSCD is 2.8 and the sample size N = 20.
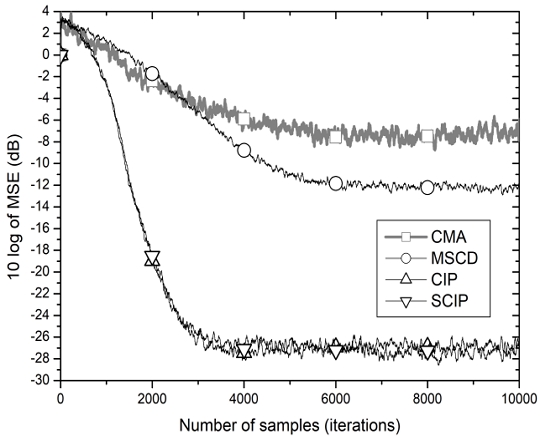
In Fig. 3 showing the MSE learning curves we may observe that the learning curve of CMA in (3) does not converge below -7 dB which indicates that CMA is inappropriate. But the CIP or SCIP algorithms show fast and stable convergence to around –27 dB. The MSE learning curves of the proposed SCIP and the conventional CIP result in similar performance with only slightly different steady state MSE of -2.7 dB and -2.75 dB, respectively. That difference can be viewed as negligible in most communication systems which usually demand performance difference of above 3 dB in order for a new system to be judged as better or superior.
We may see that this property of performance equality that the SCIP has reveals that the interactions between yk and symbol points {A1,A2,...,AM} are enough for the weight update to count in rather than considering all the interactions of {yk,yk-1,⋯,yk-N+1} and the symbol points {A1,A2,...,AM}.
Besides this property, the proposed SCIP algorithm has a figure of merit that its computational complexity in multiplication is remarkably reduced. For the sake of convenience of comparison, 2/σ2 and the Gaussian kernel Gσ(Am - yi) which commonly exist in both methods, CIP in (10) and SCIP in (11), are treated as constants.
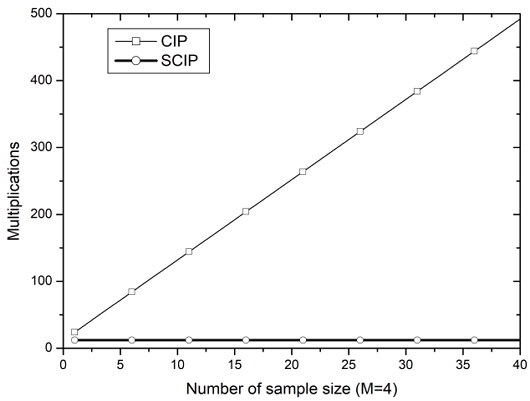
The block-processing method (10) demands 3MN multiplications at each iteration time while the proposed method (11) requires 3M multiplications. It is important that the computational complexity of the proposed one is not related with the sample size since a large sample size is preferable in order to guarantee a desired level of accuracy[15].
Fig. 4 shows the number of multiplications with respect to sample size and it is apparent that the proposed SCIP algorithm is more appropriate to practical implementations.
On the other hand, the assumption that the current output yk has more useful information than all other samples {yk-1,⋯,yk-N+1} can be verified through the performance comparison of the system error distribution which depicted in Fig. 5. In Fig. 5, the error distribution of case A which considers only the interactions between the current output yk and the symbol points {A1,A2,...,AM} has a bell shape distribution narrow enough to gather most error samples near zero. The contribution to error performance enhancement by adding the interactions between the past output yk-1 and the symbol points is insignificant as we can see in the case B. We can also observe the similar results in case C where the interactions between yk-1, yk-2 and the symbol points are added. This indicates that the information the current output sample yk has is the most useful of all other outputs.
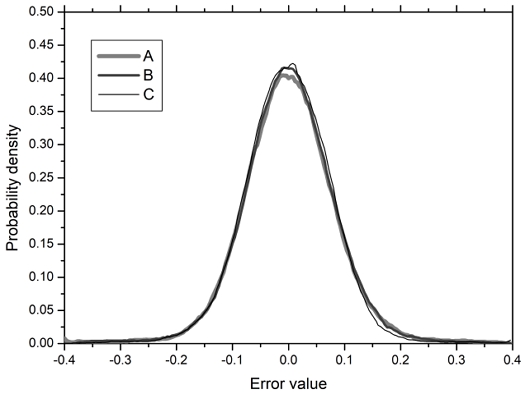
System error distribution for several interactions (A: between yk and the symbol points, B: between yk, yk-1 and the symbol points, C: between yk, yk-1, yk-2 and the symbol points)
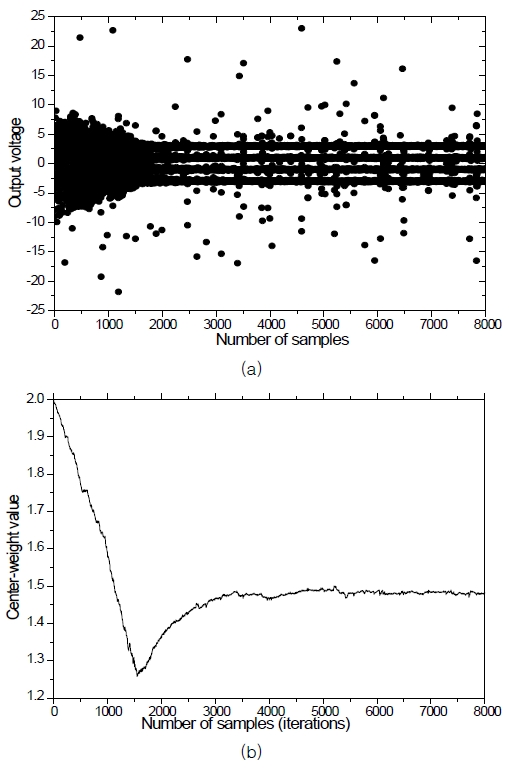
It is noticeable how the impulsive noise is processed in the learning algorithm SCIP. The resulting output signal in Fig. 6(a) shows that the output samples gather on their corresponding target symbol points after convergence though the impulses are not removed. The weight trace (the center weight is chosen for convenience’s sake) in (b) verifies the robustness of SCIP by showing that it converges its steady state value without any disturbance or fluctuations even under the strong impulsive noise.
Ⅵ. Conclusion
For overcoming the multipath channel distortions and non-Gaussian noise effects, many performance criteria and related blind algorithms have been developed based on the information potential concept which was built onprobability estimation. Despite its superior performance in non-Gaussian impulsive noise, the algorithms require heavy computational burden due to a large sample size for guaranteeing a desired level of accuracy of probability estimation. The proposed performance criterion and weight update algorithm significantly reduces the computational complexity without noticeable loss of performance in unsupervised learning and impulsive noise situations. This indicates that the proposed algorithm can replace the supervised MEE algorithms for unsupervised learning not needing training data and the CIP algorithm for reduced complexity. We may conclude thatthe proposed SCIP algorithm can be more appropriate to practical implementations than the conventional CIP algorithm.
Acknowledgments
This research was supported by “Regional Innovation Strategy (RIS)” through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (2022RIS-005)
References
-
F. Mazzenga, “Channel Estimation and Equalization for M-Qam Transmission with a Hidden Pilot Sequence,” IEEE Transactions on Broadcasting, Vol. 46, No. 2, pp. 170-176, June 2000.
[https://doi.org/10.1109/11.868934]

-
L. M. Garth, “A Dynamic Convergence Analysis of Blind Equalization Algorithms,” IEEE Transactions on Communications, Vol. 49, No. 4, pp. 624-634, April 2001.
[https://doi.org/10.1109/26.917769]

-
W. M. Moh and Y. Chen, “Multicasting Flow Control for Hybrid Wired/Wireless ATM Networks,” Performance Evaluation, Vol. 40, No. 1-3, pp. 161-194, March 2000.
[https://doi.org/10.1016/S0166-5316(99)00074-7]

-
R. Johnson, P. Schniter, T. J. Endres, J. D. Behm, D. R. Brown, and R. A. Casas, “Blind Equalization Using the Constant Modulus Criterion: A Review,” Proceedings of the IEEE, Vol. 86, No. 10, pp. 1927-1950, October 1998.
[https://doi.org/10.1109/5.720246]

-
N. Kim, H.-G. Byun, Y.-H. You, and K. Kwon, “Blind Signal Processing for Impulsive Noise Channels,” Journal of Communications and Networks, Vol. 14, No. 1, pp. 27-33, February 2012.
[https://doi.org/10.1109/JCN.2012.6184548]

- J. Principe, D. Xu, and J. Fisher, Information Theoretic Learning, in Unsupervised Adaptive Filtering, New York, NY: Wiley, pp. 265-319, 2000.
-
N. Kim, “Step-Size Normalization of Information Theoretic Learning Methods Based on Random Symbols,” Journal of Internet Computing and Services, Vol. 21, No. 2, pp. 49-55, April 2020.
[https://doi.org/10.7472/jksii.2020.21.2.49]

- S. Haykin, Adaptive Filter Theory, 4th ed. Upper Saddle River, NJ: Prentice Hall, 2001.
-
D. Erdogmus and J. C. Principe, “An Error-Entropy Minimization algorithm for Supervised Training of Nonlinear Adaptive Systems,” IEEE Transactions on Signal Processing, Vol. 50, No. 7, pp. 1780-1786, July 2002.
[https://doi.org/10.1109/TSP.2002.1011217]

-
Y. Li, B. Chen, N. Yoshimura, and Y. Koike, “Restricted Minimum Error Entropy Criterion for Robust Classification,” IEEE Transactions on Neural Networks and Learning Systems, Vol. 33, No. 11, pp. 6599-6612, November 2022.
[https://doi.org/10.1109/TNNLS.2021.3082571]

-
N. Kim and K. Kwon, “A Simplified Minimum Error Entropy Criterion and Related Adaptive Equalizer Algorithms,” The Journal of Korean Institute of Communications and Information Sciences, Vol. 48, No. 3, pp. 312-318, March 2023.
[https://doi.org/10.7840/kics.2023.48.3.312]

-
I. Santamaria, P. P. Pokharel, and J. C. Principe, “Generalized Correlation Function: Definition, Properties, and Application to Blind Equalization,” IEEE Transactions on Signal Processing, Vol. 54, No. 6, pp. 2187-2197, June 2006.
[https://doi.org/10.1109/TSP.2006.872524]

-
N. Kim, “Kernel Size Adjustment Based on Error Variance for Correntropy Learning Algorithms,” The Journal of Korean Institute of Communications and Information Sciences, Vol. 46, No. 2, pp. 225-230, February 2021.
[https://doi.org/10.7840/kics.2021.46.2.225]

-
E. Parzen, “On Estimation of a Probability Density Function and Mode,” The Annals of Mathematical Statistics, Vol. 33, No. 3, pp. 1065-1076, September 1962.
[https://doi.org/10.1214/aoms/1177704472]

-
Y. Zheng, J. Jestes, J. M. Phillips, and F. Li, “Quality and Efficiency for Kernel Density Estimates in Large Data,” in Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data (SIGMOD ’13), New York: NY, pp. 433-444, June 2013.
[https://doi.org/10.1145/2463676.2465319]

저자소개

1986년:연세대학교 전자공학과(학사)
1988년:연세대학교 대학원 전자공학과 (석사)
1991년:연세대학교 대학원 전자공학과 (박사)
1992년~1998년: 카톨릭 관동대학교 부교수
1998년~현 재: 강원대학교 전자정보통신공학과 교수
※관심분야:통신 신호처리, 정보이론적 학습

1993년:강원대학교 컴퓨터과학과(학사)
1995년:강원대학교 대학원 컴퓨터과학과(석사)
2000년:강원대학교 대학원 컴퓨터과학과(박사)
1998년~2002년: 동원대학 인터넷정보과 교수
2002년~현 재: 강원대학교 전자정보통신공학과 교수
※관심분야:패턴 인식 (Pattern Recognition), 사물 인터넷 (IoT) 응용, 기계학습