비유클리드 공간 분할을 위한 구면좌표계 기반 Octree의 특징과 한계 분석
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
3차원 공간에서 기하 정보의 효율적인 저장과 탐색을 위해 주로 직교좌표계에서 octree 또는 kd-tree 등과 같은 공간 분할 방식이 사용된다. 이에 비해, 비유클리드 공간 분할 방식은 내재된 잠재력과 가능성에도 불구하고 상대적으로 연구가 활발하지 않다. 본 논문에서는 비유클리드 공간 분할 방식인 구면좌표계 기반 octree(S-Octree)의 특성과 적용 분야, 한계를 살펴봄으로써 비유클리드 공간 분할 방식의 가능성과 발전 방향을 모색하고자 한다. S-Octree의 한계로 먼저 특정 영역에서 발생하는 불연속 문제를 논의하고 그 다음 각도 기반 기하 정보 처리 방식에서 흔히 발생하는 수치 오류가 S-Octree에서는 어떠한 양상으로 발생하는지 실험을 통해 살펴본다. 이러한 수치 오류는 연산이 연속적으로 수행됨에 따라 누적되는데 누적된 오류가 상한으로 수렴하는 사례들을 제시한다. 또한 보다 나은 새로운 비유클리드 공간 분할 기법에서 요구되는 회전 비의존성을 논의한다.
Abstract
To efficiently retrieve and store geometry information in three dimensional space, those partitioning grids including the octree and kd-tree defined in the Cartesian coordinates are often used. Unlike this, partitioning grids defined in non-Euclidean space are relatively not fully studied. In this paper, I present and discuss the features, applications, and limitations of a non-Euclidean space partitioning method, S-Octree, which is defined in the spherical coordinates to gain some insights for better methods. First, I show discontinuity issues that happen at near certain points. Then, I present how those numerical errors typically occur with angle-based geometry information processing algorithms affect S-Octree by experiments. Those errors can be accumulated by repeated conversions but I represent some cases where the accumulated errors converge to upper bounds. Also, I discuss the rotational invariance for those features required in better new non-Euclidean space partitioning methods.
Keywords:
Non-Euclidean space partitioning, Spherical coordinates, Octree, S-Octree, Numerical errors in angle-based geometry processing키워드:
비유클리드 공간 분할, 구면좌표계, 옥트리, 각도 기반 기하 정보 수치 오류Ⅰ. 서 론
3차원 공간 상에서 신속한 정보 검색을 수행하기 위해 octree, kd-tree, BVH(Bounding Volume Hierarchy) 등 다양한 검색 계층 구조, 또는 공간 분할 구조를 사용한다. 이러한 구조는 보통 직교 좌표계에 기초해서 x, y, z 좌표축과 평행하거나 수직인 평면으로 둘러싸인 bounding box를 계산하고 이 bounding box의 계층 분할 구조를 형성함으로써 구성한다.
그러나 이러한 직교좌표에서는 3차원 공간 상에서 곡면이 마치 계단처럼 표시되는 앨리어싱(aliasing) 문제[1]가, 발생하고 사람의 머리, 과일, 공 등과 같이 구와 형태가 비슷한 3차원 물체의 기하 정보의 정보 엔트로피[2]가 최적화되지 않는 한계가 있다.
이 문제를 극복하기 위한 시도들 중 하나로 구면좌표계나 원통좌표계와 같은 비유클리드 공간에서 octree를 정의해서 3차원 mesh 압축[3], [4], 3차원 공간 검색[5], 음함수 표면의 폴리곤화[6]를 위한 용도로 연구가 진행되었다.
그러나 기존 연구들에서 논의되지 않은 구면좌표계 상에서의 octree (이하 S-Octree)에 대한 분명한 한계가 존재하며 이러한 한계로 인해 앞서 언급한 우수한 특성에도 불구하고 S-Octree의 적용 범위가 제한되어 왔다. 본 논문에서는 한동안 정체되어 왔던 직교좌표계를 넘어선 새로운 비유클리드 공간으로의 확장을 위한 연구의 기초가 될 수 있도록 그동안 논의되지 않았던 S-Octree의 문제점과 한계를 논의한다.
Ⅱ. 구면좌표계와 Octree
2-1 구면좌표계
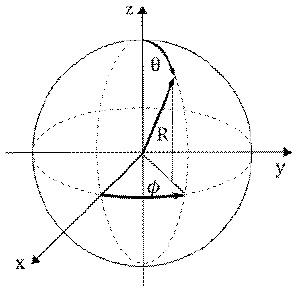
구면좌표계 (R, θ, ϕ)는 3차원 공간상에서 직교좌표계 (x,y,z)에 대해 다음 관계를 통해 정의된다.
| (1) |
| (2) |
구면좌표계는 점 전하로 인해 공간상에 형성되는 전기장의 크기 등 원점을 중심으로 방사상으로 대칭적인 물리량을 가지는 물리 방정식을 풀기 위한 용도로 흔히 사용된다. 또한 구면좌표계를 적용하면 반지름이 r인 구의 표면 위의 비유클리드 기하 정보들은 2차원 정보 (θ, ϕ)만으로 처리 가능하다. 이러한 구면좌표계의 특징은 곡면으로 표현되는 3차원 형상에서 측지선(geodesic) 등과 같이 비유클리드 기하 공간에서의 기하 정보 해석에 유리하다.
2-2 구면좌표계 기반 Octree
Octree는 기하 공간 검색, 충돌처리, 압축 등에 널리 사용되는 공간 분할 방식으로 대상 기하 정보를 감싸는 축정렬 방식 바운딩박스(Axis Aligned Bounding Box, AABB)를 구한 후 x, y, z 축에 대해 각 구간을 이진 분할함으로써 구할 수 있다. 따라서 octree는 1차원 구간에 적용하는 이진 분할의 3차원 확장 버전이라고도 할 수 있다.
따라서 각 축별로 기하정보가 존재하는 구간을 이진 분할하는 아이디어를 다른 좌표계에도 그대로 적용할 수 있다.
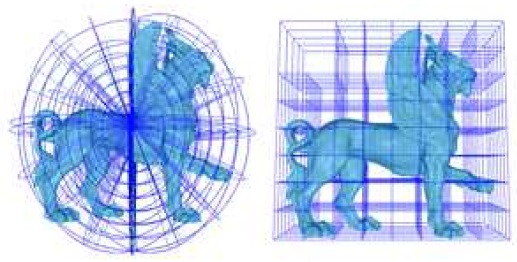
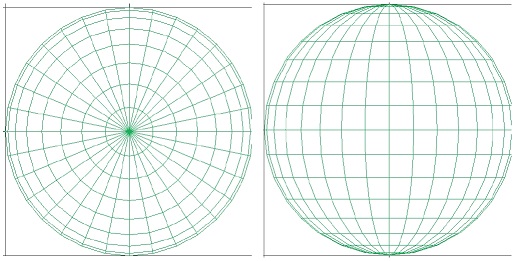
Octree defined in spherical coordinates (“S-Octree”, left) vs. that in the usual Cartesian coordinates (“C-Octree”, right).
S-Octree 역시 이러한 아이디어를 통해 정의된다. 임의의 3차원 mesh M을 구면좌표계에서 나타냈을 때 바운딩스피어(bounding sphere)의 범위가 (R, θ, ϕ)에 대해 각각 [0,Rmax], [θmin,θmax], [ϕmin,ϕmax]일 때 일반적인 직교좌표 기반 octree에서처럼 각 셀(cell)에 지정된 vertex의 개수에 도달할 때까지 분할한다.
2-3 응용 분야
일반적으로 3dsMAX, Blender와 같은 3차원 모델링 도구를 이용해서 캐릭터의 형상을 제작하는 경우 일반적으로 좌우측 중 한쪽 절반만 제작한 후 이후에 대칭(mirror) 복제를 통해 나머지 부분을 완성한다.
그림 3에서는 3dsMAX에서 동물 캐릭터 메시 모델을 제작하는 과정을 제시한다. 왼쪽 화면은 여러 모델링 도구를 이용해서 오른쪽 절반에 해당하는 모델을 제작한 모습이고 이 절반 메시 모델을 3dsMAX의 Symmetry modifier를 이용해서 yz 평면에 대칭 복제를 수행함으로써 왼쪽 절반 부분을 생성함으로써 전체 모델을 완성하는 과정을 볼 수 있다.

The process to complete a character model by applying the Symmetry modifier to a half mesh model in 3dsMAX
이러한 모델링 방식은 보편적인 방식이며 구체에 가까운 사람의 얼굴을 제작할 때에도 동일한 방식을 사용한다. 따라서 사람의 얼굴 메시를 압축하기 위해 기존의 직교 좌표 기반보다 구형에 가까운 물체의 정보를 보다 효율적으로 표현할 수 있는 구면 좌표계에서 절반에 해당하는 영역(일반적으로 0 ≤ ϕ ≤ π 영역)에 포함되는 메시의 꼭지점들과 연결 정보를 S-Octree로 재구성하고 압축함으로써 압축의 효율을 극대화하는 연구가 제안된 바 있다[3]. 특히 이 방식은 절반의 영역만 S-Octree로 구성함으로써 III장에서 살펴볼 S-Octree의 한계들 중에서 S-Octree에서 ϕ = -π에 해당하는 공간과 ϕ = π에 해당하는 공간 사이에 발생할 수도 있는 불연속 구간(그림 X)으로 인한 문제를 원천적으로 피할 수 있다는 장점도 제공한다. 또한 직교 좌표 기반 octree에 비해 S-Octree에서는 구면에 가까운 표면 상의 점들(vertices)이 R축에 대해서는 좁은 범위 내의 값을 가지게 되어 정보 엔트로피(information entropy)가 감소하여 상대적으로 높은 압축률을 실현할 수 있다.
Dual contouring 폴리곤화 기법[7]은 음함수 표면을 메시로 표현하기 위해 일반적으로 사용되는 marching cube 방식[8]에 비해 기하 정보뿐만 아니라 법선 벡터를 사용해서 메시를 구성함으로써 매끈한 표면을 좀 더 잘 표현할 수 있는 장점을 제공한다. 크기가 동일한 격자를 사용하는 marching cube 폴리곤화 방식에 비해 dual contouring은 octree를 사용하는데 곡면에 보다 적합한 구면 좌표계의 장점을 반영하기 위해 [6]에서는 dual contouring을 S-Octree 상에서 구현함으로써 이러한 장점을 극대화하고자 하였다. 이 적용에서도 그림 X에서 볼 수 있는 ϕ = -π와 ϕ = π 사이의 불연속 구간이 발생하는데 메시가 소실되는 이 부분을 ghost node라고 하는 개념을 적용함으로써 제거하였다.
Ⅲ. S-Octree의 한계
지금까지 논의한 것처럼 S-Octree는 구형에 가까운 3차원 도형을 효율적으로 나타낼 수 있으나 기존 연구에서는 논의되지 않은 한계로 인해서 적용이 제한적이었다. III장에서는 S-Octree의 적용을 제한해 온 구현과 관련된 한계점을 논의한다.
3-1 YZ 평면 주변의 정의되지 않는 영역
수식 (1)을 통해 직교 좌표 상의 한 점 (x,y,z)를 구면 좌표 상의 한 점 (R, θ, ϕ)으로 변환하기 위해서는 를 계산할 필요가 있다. 그러나 x=0인 yz 평면과 그 주변 공간에 포함된 점들을 변환하기 위해 수식 (1)을 그대로 적용할 수 없으며 실제로는 다음과 같은 연산이 적용된다.
| (3) |
일반적으로 널리 알려진 것처럼, 실제 구현에서는 IEEE 754 표준에 의한 32 비트 또는 64 비트 부동소숫점 실수의 표현 방식의 한계로 인해 정확하게 x=0.0으로 표현할 수 없고 매우 작은 실수 ε으로 0.0에 해당하는 범위를 표현하게 된다. 따라서 YZ 평면과 그 주변의 점들은 직교좌표에서 구면좌표로, 또는 구면좌표에서 직교좌표로 변환할 때 정보의 소실 또는 위치의 왜곡이 발생할 가능성이 있으며 수식 (2)에 의해 R이 클수록, 즉, 원점에서 먼 점일수록 이러한 오류가 증가할 가능성이 높아진다고 가정할 수 있다.
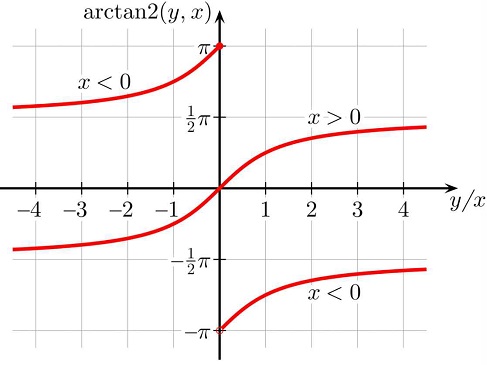
C/C++ 또는 Python 등과 같은 프로그래밍 언어로 직교좌표/구면좌표 사이의 변환을 구현할 때 식 (3)에서 등장하는 은 x=0일 때 값이 정의되지 않기 때문에 여러 프로그래밍 언어에서는 artan2(y, x) 또는 atan2(y, x) 함수를 제공한다. 이 함수는 x=0일 때에도 정확한 값을 제공할 수 있도록 구현되었다. 그림 4에는 arctan2(y,x)의 그래프를 제시한다.
이 그래프에서 볼 수 있는 것처럼 arctan2 함수는 x < 0일 때 y/x = 0에서 불연속이라는 사실에 주의해야 한다. 이러한 문제 때문에 S-Octree로 메시를 구성하면 ϕ = -π와 ϕ = π가 일치하는 방향(즉, x의 음의 방향)으로 이 불연속 지점이 발생할 수 있다(그림 5).
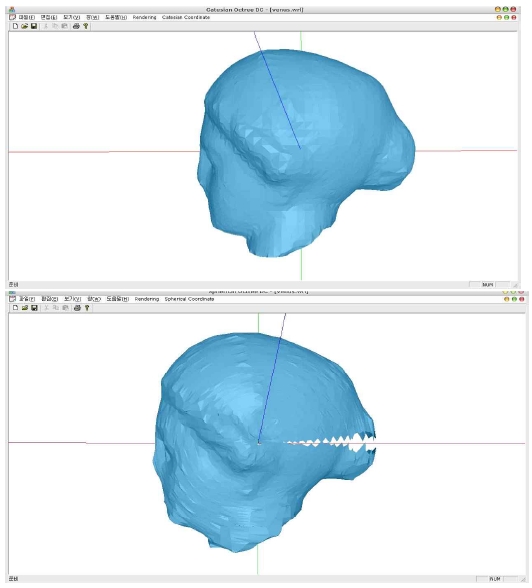
Polygon meshes constructed in the Cartesian coordinates (top) and in the spherical coordinates (bottom)
앞서 논의한 것처럼 [6]에서는 이렇게 메시가 소실되는 이 부분을 ghost node라고 하는 개념을 적용해서 인위적으로 불연속성을 연결함으로써 제거하였으나 구면 좌표를 기반으로 하는 비유클리드 기하 분석에서는 실제로 연속적인 공간이 변환을 통해 불연속적인 함수로 해석될 수도 있다는 점에 유의해야 한다.
3-2 삼각함수로 인한 수치 오류
일반적으로 3차원 공간에서 정의되는 3차원 형상 정보는 고차원 음함수로 표현 가능하지만 실제 응용에서 연산 효율성을 확보하기 위해 고차원 음함수의 1차 근사라고 할 수 있는 삼각형 메시(mesh)를 이용한다. 삼각형들은 기본적으로 1차식으로 표현되는 평면의 일부분이며 따라서 삼각형 메시는 1회 미분 가능한 C1 함수이다. 고급 기하 정보 처리 이론은 기하 정보의 미분 가능성에 의존하며 여러 미분 기하(differential geometry) 방정식들은 메시에서 1차 근사 또는 차분 기하(difference geometry) 방정식으로 변환해서 이산적으로 계산을 하는 방식이 일반적이다. 이러한 과정에서 메시를 구성하는 삼각형의 형태가 중요하며 둔각삼각형(obtuse triangle)이 포함될 경우 barycentric 좌표 계산 등에서 여러 문제가 발생하게 된다. 따라서 ‘고품질 메시’란, 둔각삼각형이 배제되고 대부분 예각삼각형 또는 정삼각형에 가까운 삼각형들로 구성되는 메시들을 의미한다.
Sharp와 동료 연구자들은 메시의 기하 정보를 ‘표지판 자료구조(signpost data structure)’[9]로 재구성함으로써 둔각 삼각형들로 구성된 저품질 메시에서도 둔각 삼각형으로 인한 오류를 최소화하는 방법을 제안하였다(그림 6).
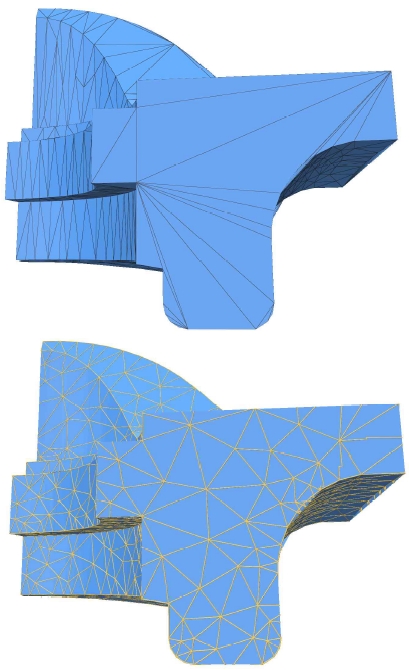
A low quality mesh with obtuse triangles (top) and a high quality mesh with acute triangles reconstructed using the ‘signpost data structure’ [9] (bottom)
표지판 자료구조의 핵심은 이상적인 예각 삼각형들로 구성되는 내재적인 삼각화(intrinsic triangulation)를 구성하기 위해 각 꼭지점(vertex)에서 주변 꼭지점들에 대한 1) 거리와 2) 방향을 저장한다. 이 때 방향은 결국 각도를 의미하며 주변 꼭지점들의 기하학적인 위치는 결국 직교좌표와 구면좌표 사이의 변환식에서처럼 삼각함수들을 이용해서 구하게 되며 각도 계산에서 수치 오류로 인한 기하 정보 오류가 누적되는 것이 일반적이다. 일반적으로 각도에 의한 기하 정보의 오류는 원 계산 지점에서 거리가 멀수록 더 증가한다.
S-Octree 역시 기본적으로 각도를 이용하는 기하 정보 처리 방식이며 기하 정보를 구면좌표로 표현하고 계산하더라도 최종적으로 직교좌표 기반인 컴퓨터 그래픽스 파이프라인을 통해서 화면에 결과물을 출력하기 위해서는 다시 직교좌표로 전환해야 한다. 이렇게 화면에 표시한 직교좌표는 사용자의 필요에 따라 인터랙티브한 방식으로 런타임 동안 다시 구면좌표로 변환된 후에 필요한 계산을 수행하고 다시 직교좌표로 변환되는 과정이 반복될 수 있다.
이러한 직교좌표와 구면좌표 사이의 전환 연산은 S-Octree의 실제 적용을 방해하는 한계로 작용하고 있으나 이 변환으로 인한 오류에 대해서는 거의 논의된 적이 없으며 본 논문에서는 1회 변환으로 인한 오류와 런타임 환경에서 여러 회 변환이 진행됨에 따라 누적되는 오류에 대해 실험을 통해 살펴본다.
좌표 변환으로 인해 발생하는 오류의 영향을 살펴 보기 위해 1회 변환(직교⟶구면⟶직교)으로 인한 오류와 런타임 환경에서 변환이 반복, 누적되어 발생되는 두 가지 경우로 나누어 실험을 수행하였다. 이 실험을 위한 코드는 libigl 라이브러리[10]를 이용해서 C++로 구현하였다.
a. 1회 변환 오류 테스트
표 1에서는 1회 변환으로 인한 L2-norm 오류(∥•∥2)를 계산하는 유사 코드를 제시한다. 이 코드에서 실수는 모두 32비트 부동소수점형식(float)을 사용했으며 오류를 계산하기 전 모든 메시는 mini ball 알고리즘[11]을 이용해서 모든 꼭지점들을 포함하는 최소 크기의 구와 그 반지름 r을 계산한 다음, 이 구의 중심이 메시의 중심점과 일치하도록 이동(translation) 변환을 수행하고 1/ r로 배율(scale) 변환을 수행함으로써 모든 꼭지점들이 반지름이 1인 단위 구(unit sphere)에 포함되도록 조정한다.
그림 7은 XY 평면(Z=0)에 위치한 직사각형 메시에 대해 표1의 알고리즘을 적용한 결과를 제시한다. 1회 변환한 L2 norm 오류는 최소의 경우 10-9 수준이고 최대의 경우 10-7으로 100 배 정도의 차이는 있으나 모두 32비트 실수 연산에서 대체로 0.0f로 인정하는 허용 가능한 범위 (적용 분야마다 차이가 있지만 수치 연산인 경우 일반적으로 10-6 이하 )임을 확인할 수 있다. 그러나 실제 응용에서는 다음 실험에서처럼 1회 변환으로 그치지 않고 여러 회 반복되어 이 오류가 누적될 수 있으며 이 실험은 모든 메시를 반지름 1인 단위 구 내로 배율을 조정했기 때문에 배율이 커지면 이 오류의 크기도 커진다는 점도 고려해야 한다.
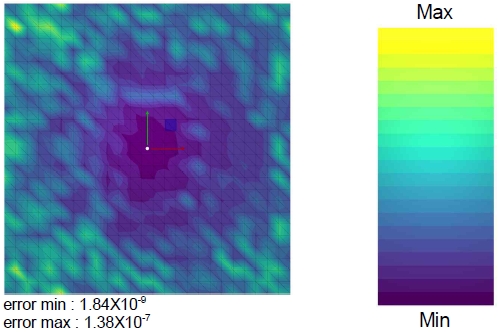
L2 errors (root mean squared errors) caused by a serial conversion operations between the Cartesian and spherical coordinates (Cartesian ⟶ spherical ⟶ Cartesian) measured on the vertices in a square plane mesh on the XY plane (Z=0). The red/green/blue arrows indicate the X/Y/Z axes respectively. Z axis is not indicated from this view.
이 실험에서 주목해야 할 점은 오차의 절대적인 크기보다도 최대 오차와 최소 오차가 100배 정도 차이가 나며 일관적으로 위치에 따라 변환 오류가 다르게 나타난다는 점이다. 그림 7을 보면 원점에 가까운 지점에서는 오차가 적지만(보라색 및 파란색) 방사상으로 원점으로부터의 거리가 증가함에 따라 변환 오차가 커지는 경향(녹색 및 노란색)을 관찰할 수 있다. 이러한 위치에 따른 오류의 경향성은 다른 일반적인 메시 모델에서도 그대로 관찰된다. 그림 8에서는 다양한 형태를 가진 메시에서의 결과를 제시한다. 대체로 메시의 중심(원점)에 가까울수록 오류가 적으며 멀어질수록 오차가 증가하는 것을 볼 수 있다. 특히 이러한 경향은 lucy와 buddha 모델처럼 한 방향으로 긴 메시에서 두드러지게 나타나고 bunny 모델의 귀 부분이나 nala의 목 부분, dragon 모델의 머리나 꼬리 부분처럼 돌출한 영역에서 오류가 증가함을 확인할 수 있다. 그림 8에서 cave 모델은 동굴 내부를 표현한 지형 모델인데 원점에서의 거리에 따른 오류의 경향성을 분명하게 볼 수 있다.
b. 오류 누적 테스트
1회 변환 오류 테스트를 통해서 (x, y, z)⟶(R, θ, ϕ)⟶(x', y', z')로 변환했을 때 특정한 영역에서는 (x, y, z) ≠ (x', y', z')라는 사실을 확인했다.
S-Octree를 구성해서 특정한 연산을 수행하더라도 그 결과는 직교좌표계로 변환해서 그래픽스 파이프라인을 통해 화면에 표현해야 하기 때문에 실시간 응용 분야에 따라서 이러한 변환이 연속적으로 적용(즉, (x, y, z)⟶(R, θ, ϕ)⟶(x', y', z')⟶(R', θ', ϕ')⟶(x″, y″, z″)⟶...)되는 상황도 발생할 수 있다.
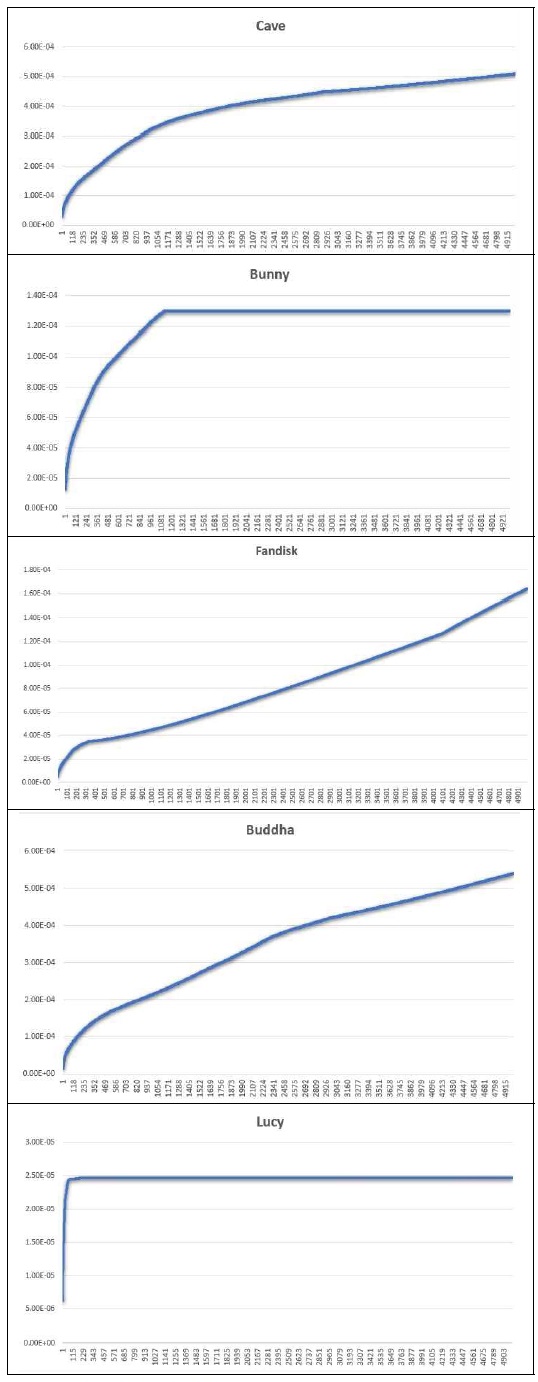
이렇게 변환이 연속적으로 수행되면 필연적으로 오류가 누적되어 원래 기하 정보와의 차이가 점점 더 커질 수도 있다. 이러한 효과를 확인하기 위해 표 2에서는 연속 좌표 변환으로 인해 누적되는 오류를 계산하기 위한 유사 코드를 제시한다. 유사 코드에서 ∥•∥F는 Frobenius norm을 의미한다. 그림 9는 표 2의 Algorithm 2에서 이 코드에서 반복 횟수를 결정하는 iter 변수를 5000으로 설정해서 5000번 직교⟶구면⟶직교 좌표 변환을 반복할 때 원본 메시와의 차이를 그래프로 표시한 것이다. 모델마다 누적되는 오류의 크기가 다르지만 대체로 10-4 수준까지 상승하는 것을 볼 수 있고 bunny와 lucy 모델의 경우 빠르게 증가한 후 일정한 오류가 지속적으로 유지는 현상을 볼 수 있다. 두 모델에서 보이는 누적 오류 수렴 현상은 32 비트 부동소수점 연산으로 인한 특성인 동시에 각 메시 모델의 기하학적인 특징에 따라 결정되는 것으로 판단되며 수렴 원리에 대한 분석 및 활용 가능성 등에 대한 추가적인 연구가 필요할 것으로 보인다.
3-3 방향/회전 의존 문제
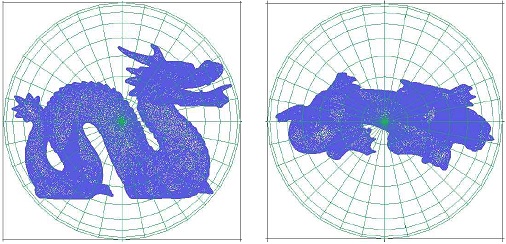
그림 10에서는 S-Octree로 구성한 격자를 볼 수 있다. S-Octree는 구면좌표계의 특성으로 인해 극(pole) 부분에는 격자 셀(cell)이 좁게 삼각 기둥 형태로 구성되며 적도 방향으로 이동하면서 부피가 증가하고 형태도 사각 기둥 형태로 구성된다. 이러한 구조적인 특징으로 인해 모델의 방향에 따라 S-Octree의 특성이 달라진다(그림 11). 양쪽 극 (θ = 0, θ = π) 지점에서는 격자 셀의 부피가 작고 밀도가 높기 때문에 평균적으로 셀 당 포함되는 꼭지점의 개수가 적은 반면 적도 () 부근에서는 셀의 부피가 크고 밀도가 낮아서 반대 현상이 발생할 가능성이 높다. 따라서 S-Octree는 모델의 방향 또는 회전에 영향을 받는 특성(rotational variance)을 가지며 향후 비유클리드 공간 확장을 위해 S-Octree와 유사한 공간 분할 격자를 설계하기 위해서는 회전 의존성 문제를 반드시 해결할 필요가 있다.
Regular grids constructed by S-Octree. The pole area viewed from the XY plane (left) and the equator area from the ZX plane (right)
Ⅴ. 결 론
비유클리드 공간 분할을 수행하는 S-Octree는 구면에 가까운 모델, 대부분 곡면으로 구성된 모델의 효율적인 저장과 검색을 실현할 수 있는 가능성을 가지고 있으나 보다 폭넓은 응용을 위해서 해결해야 하는 문제들이 있다. 본 논문에서는 S-Octree의 적용 분야를 조망해 보고 보다 폭넓은 적용을 막고 있는 주요 문제들을 살펴 본다.
먼저 ϕ = -π와 ϕ = π가 일치하는 방향(즉, x의 음의 방향)으로 이 불연속 지점이 발생하는 문제를 논의하고 기존에 제안되었던 해결 방법을 살펴 보았다.
그리고 기하 정보의 활용을 위해 각도를 기반으로 특정한 처리를 수행하는 응용에서는 흔히 수치 오류가 발생하고 연속적인 변환에서 이러한 오류가 누적된다. 본 논문에서는 직교좌표와 구면좌표 변환 과정에서 발생하는 오류가 주로 원점에서 먼 곳에서 크게 발생되며 일련의 변환이 수행될 때 오류가 누적되어 증가하지만 몇몇 모델에서는 특정한 상한값으로 수렴함을 실험적으로 제시하였다. 수렴되는 상한값은 모델의 기하학적인 특성에 따라 결정되는 것으로 보이며 향후 추가 연구를 통해 수렴되는 오류 상한값과 기하학적인 특성의 상관관계를 검토해 볼 필요가 있고, 동시에 오류 최소화를 위한 직교좌표계에서의 이산화 방법 등에 대한 새로운 연구로 이어질 수 있을 것으로 기대한다.
마지막으로 S-Octree의 가장 큰 단점 중 하나인 회전 의존성을 살펴보고 그 원인에 대해서 논의하였다. 이러한 회전 의존성을 해결하기 위해서는 같은 레벨에서는 각도 좌표에 상관없이 크기와 모양이 일정한 새로운 비유클리드 공간 분할 격자 방식이 설계되어야 할 것이다.
Acknowledgments
본 연구는 덕성여자대학교 2020년도 교내연구비 지원에 의해 수행되었음.
References
-
F. C. Crow, “The aliasing problem in computer-generated shaded images,” Communications of the ACM, Vol. 20, No. 11, pp. 799–805. Nov. 1977.
[https://doi.org/10.1145/359863.359869]

-
C. E. Shannon,. "A Mathematical Theory of Communication," Bell System Technical Journal. Vol. 27, No. 3, pp. 379–423, July 1948.
[https://doi.org/10.1002/j.1538-7305.1948.tb01338.x]

-
T. Park, S.-J. Kang, and C.-H. KIM, “Face Mesh Compression Based on Half-Spherical Coordinates for Home Entertainment Systems,” in IEEE International Conference on Consumer Electronics (ICCE), pp. 701-702, Jan. 2011.
[https://doi.org/10.1109/ICCE.2011.5722818]

- T. Park, S.-J. Kang, and C.-H. KIM, “Face Mesh Compression Based on S-Octree for Game Characters,” Journal of Korean Society for Computer Game, Vol. 25, No. 1, pp. 67-78, March, 2012.
- T. Park, S.-H. Lee, C.-H. Kim, “S-Octree: An Extension to Spherical Coordinates,” Journal of Korea Multimedia Society, Vol.13 No.12, pp. 1748-1759, Dec. 2010.
-
J.-H., Kim, T. Park, and C.-H. Kim, “Enhanced Dual Contouring method by using the Feature of Spherical Coordinate System,” Journal of the Korea Computer Graphics Society, Vol. 17, No. 2, pp. 27-36, June 2011.
[https://doi.org/10.15701/kcgs.2011.17.2.27]

-
T. Ju, F. Losasso, S. Schaefer, and J. Warren. "Dual contouring of hermite data," In Siggraph 2002, Computer Graphics Proceedings, pp. 339-346. July 2002.
[https://doi.org/10.1145/566654.566586]

-
W. E. Lorensen, "History of the Marching Cubes Algorithm," in IEEE Computer Graphics and Applications, Vol. 40, no. 2, pp. 8-15, March-April 2020.
[https://doi.org/10.1109/MCG.2020.2971284]

-
N. Sharp, Y. Soliman, and K. Crane, “Navigating intrinsic triangulations,” ACM Transactions on Graphics, Vol. 38, No. 4, pp. 1–16. August 2019.
[https://doi.org/10.1145/3306346.3322979]

-
A. Jacobson, Daniele Panozzo, and others, “libigl : A simple C++ geometry processing library”, https://libigl.github.io, , 2018.
[https://doi.org/10.1145/3134472.3134497]

-
B. Gärtner, “Fast and Robust Smallest Enclosing Balls,” In J. Nešetřil (Ed.), Algorithms—ESA’ 99, pp. 325–338, July 1999.
[https://doi.org/10.1007/3-540-48481-7_29]

저자소개

1997년 : 서울대 전기공학부 (공학사)
1999년 : 서울대 전기공학부 대학원 (공학 석사, 반도체 물리 전공)
2006년 : 서울대 전기컴퓨터공학부 대학원 (공학박사, 컴퓨터 그래픽스 전공)
2018년~현 재 : 덕성여자대학교 공과대학 사이버보안/IT미디어공학과 부교수
2013년~2017년 : 덕성여자대학교 정보미디어대학 디지털미디어학과 조교수
2006년~2013년 : 고려대학교 연구교수
※관심분야:컴퓨터그래픽스, 병렬처리, 인공지능, 수치해석, 3차원 모델링