정밀도 개선을 위한 순열 기반 추가 루프를 적용한 이동 정렬 기반 근사 k개 최근접 검색 알고리즘
Copyright ⓒ 2021 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
인공지능과 빅데이터의 적용 범위가 확대됨에 따라 다차원 벡터 공간 상에서 특정한 질의 지점을 나타내는 벡터로부터 가장 가까운 순서로 k개의 데이터 벡터를 찾는 알고리즘(kNN)이 다양한 분야에서 활용되고 있다. 특히 자율주행과 같은 실시간 애플리케이션, 실시간 온라인 문서 검색 등에 대한 수요가 증가하면서 kNN 알고리즘의 병렬화, 고속화가 진행되고 있다. 이러한 실시간 애플리케이션에 적용하기 위해 어느 정도의 정밀도를 희생하면서 빠른 시간 내에 검색을 수행하는 근사 k개 최근접 검색 알고리즘(kANN)도 널리 사용되고 있으며 shifted sorting 기반 kANN 알고리즘은 GPU 병렬처리에 적합한 구조를 가지고 있다. 그러나 shifted sorting 기반 kANN 알고리즘은 정밀도를 컨트롤 할 수 있는 방안이 연구되지 않았다는 한계가 있다. 본 논문에서는 기존 shifted sorting 기반 kANN 알고리즘의 원리를 살펴 봄으로써 정밀도를 개선할 수 있는 방안을 논의하고 구체적인 방식으로 각 축의 순서를 순열을 통해 재배치한 후 Morton 코드를 생성하고 기존 방법을 적용함으로써 약간의 시간을 희생하고 상대적으로 높은 정밀도를 달성하는 개선 방안을 제안한다.
Abstract
The k-nearest neighbor (kNN) search algorithm - which finds the k-nearest data vectors for query vectors - has been increasingly applied to various applications including artificial intelligence and big data analysis. Some realtime applications like autonomous driving and online document search require fast parallel kNN algorithms for fast response to environment or user interaction. For this purpose, the k-approximate nearest neighbor (kANN) searching algorithms reduce process time with sacrification of certain level of accuracy. Among various approaches, the shifted sort-based kANN method is well suited for GPU parallel implementation but there have been no ways to control accuracy of the results. In this paper, I examine and discuss the feature of shifted sort-based kANN method which affects accuracy and present a method to improve its accuracy. The suggested method adopts extra loops based on permutation of vector axes for better accuracy. The test results show that we can achieve improvement in accuracy at a slight cost of increased processing time.
Keywords:
k-Approximate Nearest Neighbor Searching Algorithm, kANN, CUDA, GPGPU, Clustering키워드:
근사 k개 최근접 검색 알고리즘, kANN, CUDA, GPU 병렬처리, 클러스터링Ⅰ. 서 론
2012년 발표된 이동 정렬 기반 근사 k개 최근접 검색(shifted sorting-based k-approximate nearest neighbor searching) 알고리즘[1]은 병렬처리 프로그래밍이 가능한 그래픽 프로세서(GPU)에서 병렬 방식으로 n차원 벡터 공간에서 p개의 데이터 벡터와 q개의 질의 벡터가 있을 때 일정한 오차를 허용(approximate)하면서 모든 q개의 질의 벡터 각각에 대해 가장 가까운 데이터 벡터부터 k번째로 가장 가까운 데이터 벡터를 찾는 기술이다. 이러한 근사 최근접 검색 방법은 실시간 애플리케이션 등에서 정밀도를 어느 정도 희생하면서 빠른 실행 시간을 실현하기 위해 설계된 방법으로 정밀도를 어느 정도 희생하기는 하지만 각 질의 벡터에 대해 발견한 k개의 최근접 데이터 벡터와의 거리는 특정한 오차 범위 내로 유지되도록 보장한다. 다시 말해서 일반적으로 특정 질의 지점에서 최근접 검색으로 k개의 데이터 벡터들을 찾았을 때 발견한 이 벡터들보다 더 가까운 데이터 벡터가 몇 개 정도는 존재할 수도 있다는 것을 의미한다. 동시에, 실제로 가장 가까운 k개 데이터 벡터와 근사적으로 찾은 데이터 벡터 사이의 거리도 일정한 오차 범위 내에 유지된다.
이러한 k개 최근접 검색 알고리즘은 특정한 질의 벡터 각각에서 엄밀하게 가장 가까운 k개의 데이터 벡터를 찾을 필요가 없고 빠른 판단이 필요한 분야에 적합하다. 예를 들어 자율주행 시스템 등에서 빠른 시간 내에 1차적으로 3차원 공간 내에서 LADAR 등으로 스캔한 3차원 지점 정보(point cloud)를 이용해서 가까운 사물까지의 대략적인 거리나 가장 가까운 사물을 대략적으로 빠르게 파악해야 하는 경우, 또는 텍스트 빅데이터 분석 등에서 word vector [2] 등의 다차원 벡터 공간에서 특정한 내용을 가지는 k건의 문서를 찾아내는 용도 등에서 적용 가능하다.
여러 근사 최근접 검색 기법들 중에서 기존의 이 shiftedsorting 기술은 동일한 목표를 달성하기 위해 사용하는 GPU 기반 kd-tree 또는 BVH 구조가 GPU 하드웨어 구조로 인해 성능 저하를 보이는 분기문(if문)에 크게 의존하는 것과는 달리 분기문에 대한 의존성을 감소시킴으로써 수행 시간 측면에서 탁월한 성능 향상을 보인다는 장점이 있다[3, 4].
그러나 근사 k 개 최근접 검색 알고리즘이 어느 정도의 오차를 허용하는 방법이긴 하지만 이 오차가 지나치게 크면 후속 작업을 통해 보정을 해야 할 필요가 발생하기 때문에 특정한 애플리케이션의 효율이 떨어지는 문제가 발생한다.
따라서 본 논문에서는 shifted sorting의 정밀도가 저하되는 근원적인 문제를 살펴 보고 약간의 시간 증가를 감수하면서도 전체적인 정밀도를 상대적으로 크게 향상시킬 수 있는 새로운 알고리즘 - permutated shifted sorting-based kANN searching - 을 제안하고 비교 결과를 제시한다.
Ⅱ. 본 론
2-1 기존 방식의 문제점 분석
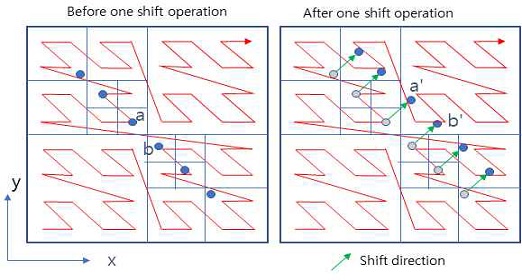
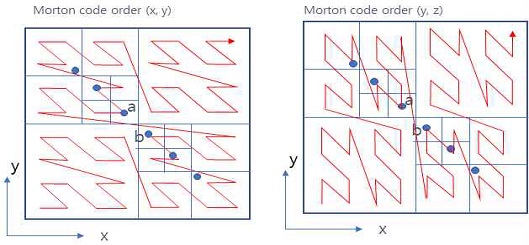
그림 1은 [1]에서 발췌한 그림으로 기존의 이동 정렬 기반 근사 k개 최근접 검색 알고리즘의 작동 방식을 제시하고 있다. n차원 벡터 공간에서 데이터 및 질의 벡터(파란색 점)가 1차원 Morton 코드 공간(분홍색 선)으로 투사된 후 이 1차원 공간에서의 근접 관계를 파악할 때의 문제(왼쪽)를 설명하고 이 문제를 해결하기 위해서 전체 벡터를 (2차원의 경우) [1,1] 벡터 방향으로 정해진 거리와 횟수(Chan의 lemma 3.3, [5]의 3.1절)만큼 이동시켜서 계산([1]의 Algorithm 1 참고)한다. 그러나 기존 shifted sorting 기술은 빠른 실행 속도가 가능하다는 장점에도 불구하고 특정 방향으로만 이동(shifted) 연산을 수행하여 정확도가 지나치게 떨어진다는 문제가 있다. 다시 말해 기존 기술이 근사 최근접 이웃 검색(kANN) 방식이라는 전제가 있기는 하지만 기존 기술이 원점에서 출발하여 벡터 공간에서 원점에서 멀어져 가는 방향으로만 정해진 정수 횟수만큼 이동한 후 질의 벡터와 데이터 벡터 모두를 Morton 코드로 투사하여 1차원 공간 상에서 정렬 후 탐색을 수행하기 때문에 실제 벡터 공간 상에서는 가깝더라도 Morton 코드 상의 1차원 공간에서는 거리가 먼 것으로 판단되어 큰 오류가 발생한다. 물론, 이러한 오류는 Chan의 lemma 3.3에 의해 허용 가능한 오차 한계 이내로 한정된다는 사실이 증명되었음에도 불구하고 기존 shifted sorting 기술은 한 마디로 다차원 데이터를 1차원 공간으로 투사하고 특정한 방향으로만 이동(shift)하면서 새롭게 발견된 가장 가까운 데이터 벡터들을 찾아서 지금까지 알고 있는 가장 가까운 데이터들을 갱신하는 과정을 거치기 때문에 오류가 발생한다고 결론을 내릴 수 있다.
2-2 정확도 개선 방안
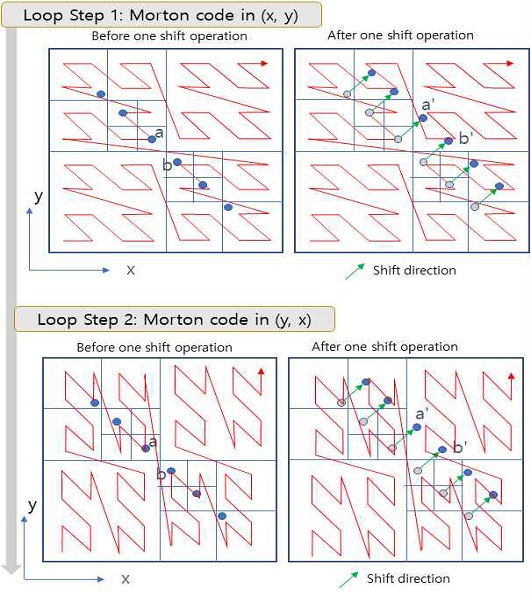
전술한 기존 shifted sorting kANN 방식은 Morton 코드를 비트 단위로 변환해서 좌표축에 대한 한 가지 순서 (x, y, z) 로만 구성한다. 이러한 구성은 합당한 이유가 있는 것은 아니고 자의적인 순서이며 기존 octree의 구현에서 child tree node 배치 구성에서의 순서의 영향을 받은 것으로 보인다. 그림 5에서 볼 수 있듯이 공간 상에서 Morton 코드를 1비트 씩 증가시키면서 진행하면 Morton 코드가 3차원인 경우 octree, 2차원인 경우 quadtree가 탐색하는 공간과 동일한 공간을 순서대로 탐색하는데 그림 3 내 왼쪽 그림에서는 (x, y) 순서대로 생성한 Morton 코드의 탐색 방향을 볼 수 있고 오른쪽 그림에서는 (y, x) 순서대로 생성한 Morton 코드의 탐색 방향을 볼 수 있다. Morton 코드의 생성 방식과 기하학적인 의미, 비트 단위의 배치의 의미에 대한 세부적인 사항은 [6]을 참고한다.
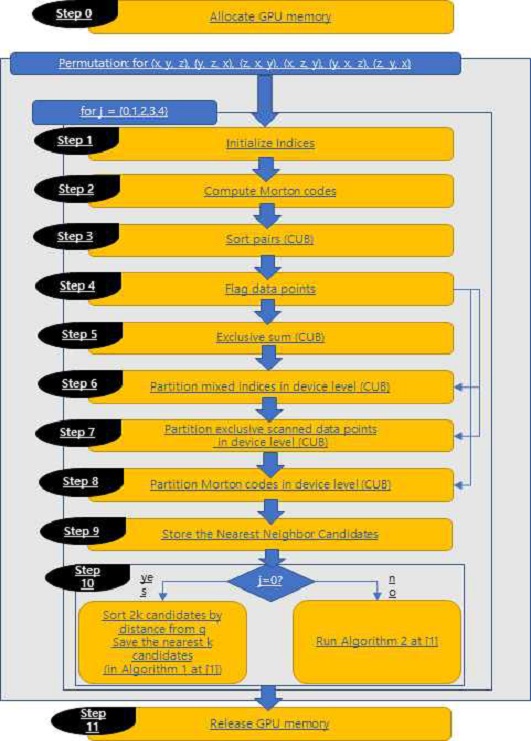
논의한 한계를 보완하기 위해 본 논문에서는 Morton 코드 상의 1차원 공간에서 실제 벡터 공간 상의 공간적 배치를 보다 정확하게 반영할 수 있도록 하여 정확도를 개선하는 새로운 알고리즘 – 순열 적용 이동 정렬 기반 근사 k개 최근접 검색(permutated shifted sorting-based kANN searching) 알고리즘을 제안한다. 제안하는 새로운 알고리즘에서는 벡터의 각 원소의 순서를 순열로 변환한 후 기존 shifted sorting kANN 연산을 반복 수행한다(그림 5). 예를 들어 3차원 벡터의 경우 3! = 6개의 순열 조합 (x, y, z), (y, z, x), (z, x, y), (x,z,y), (y,x,z), (z,y,x)에 대해 각각 기존 shifted sorting의 연산을 수행하게 되는데 이러한 6개의 순열에 대해 각각 3차원 기하 정보를 1차원 기하 정보인 Morton 코드로 변환하여 1차원 Morton 코드 상에서 각 질의 지점을 기준으로 가장 가까운 k개의 데이터 지점 업데이트를 수행한다.
예를 들어 2차원 예제의 경우 기존 방법은 그림 4에서 2차원 공간 상에서 질의 점 및 데이터 점(파란색 점)의 유클리드 거리 기준 최근접점을 근사적으로 찾기 위해 연산을 줄일 수 있는 1차원 공간인 Morton 코드(빨간색 선) 상에서의 순서(빨간색 선 상의 화살표로 표시)를 기준으로 데이터를 정렬한 후 이 1차원 공간 상에서 서로의 거리를 측정한다.
(x, y) 순서로만 Morton 코드를 생성한 후 이동시키는 기존 방법(그림 1)에서 볼 수 있듯이 Shift 연산 전에는 2차원 공간 상에서 가까운 점 a와 b가 실제로 가깝지만 1차원 공간인 Morton 코드 상에서는 아주 먼 거리로 파악한다.
따라서 기존 방법에서는 일정한 거리를 shift시킨 후 1차원 Morton 코드 상에서 각 점과 가장 가까운 점을 계속 기억하면서 새로운 가까운 점이 나타나면 가장 가까운 점들의 정보를 갱신한다. 그러나 xy 순서로만 1차원 Morton 공간을 생성해서 탐색하는 기존 방식은 2차원 공간에서 실제로 가까움에도 불구하고 1차원 Morton 공간에서 먼 것으로 파악하는 문제가 여전히 발생하는데 또한 이 문제는 데이터/질의 지점의 차원이 증가하더라도 1차원 Morton 코드에서만 최근접점들을 찾는데 차원이 증가하면 실제로 가까움에도 불구하고 1차원 Morton 공간에서 먼 것으로 파악하는 문제의 발생 빈도가 더 증가한다.
이 논문에서 제안하는 방법에서는 이러한 누락되는 정보가 발생하는 빈도를 줄이기 위해 Morton 코드를 구성할 때 순열을 적용하고 기존 shifted sort 정렬 방식을 반복함으로써 Morton 코드가 보다 정확하게 가까운 최근접점들을 찾을 수 있도록 한다. 따라서 그림 4에서 제시하듯이 제안하는 방식에서는 오른쪽에서 2차원 사례에 대해 (x, y)뿐만 아니라 (y, x)를 기준으로도 Morton 코드를 구성하고 검색을 실행한다. 이 과정은 제안하는 알고리즘을 정리한 그림 5에서 step 1부터 반복 수행되는 외부 루프로 적용된다.
이렇게 다차원 벡터에서 모든 순열을 조합하여 Morton 코드를 구성하고 각 Morton 코드에서 최근접점을 찾음으로써 알고리즘의 정밀도를 향상시킬 수 있다. 또한 3차원 벡터뿐만 아니라 보다 일반적인 n차원 벡터로의 확장도 가능하며 n차원 벡터의 경우 n!개의 순열 조합을 적용한다.
2-3 기존 방식과의 성능 비교
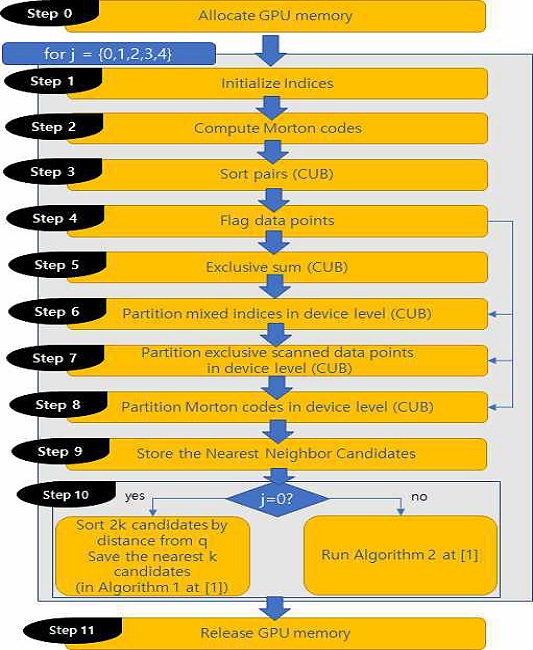
이 절에서는 제안하는 솔루션을 평가하기 위한 테스트 방식과 결과를 논의한다. 테스트 환경으로 Intel Xeon CPU 2.20 GHz, RAM 125GB 하드웨어 환경에서 구동되는 Ubuntu 18.04 LTS OS에서 CUDA 10.2 버전으로 작동하는 NVIDIA 2080Ti GPU 1개를 사용하여 테스트를 수행하였다. 테스트 결과, 제안하는 솔루션의 경우 n차원 벡터에 대해 n! 회만큼 반복 연산이 추가되기 때문에 전체적인 시간은 n!에 선형적으로 비례해서 증가할 것으로 예상되었으나 표 1에서 제시한 것처럼 추가된 루프로 인한 시간 증가는 선형적으로 증가하지 않고 선형적인 시간 증가보다 약간 감소하는 경향을 보였다. 이러한 특징은 GPU 처리를 위한 CUDA 아키텍처가 컴파일러 차원에서 컴파일 전 루프의 반복 횟수(여기에서는 3!=6회)가 알려진 경우 최적화(loop unrolling)[7]를 수행하고, 동시에 병렬 방식으로 처리할 데이터의 양이 많아지면 GPU 내 warp 스케줄러의 성능이 최적화[8]되어 성능이 증가하기 때문으로 판단된다. 따라서 그림 2의 코드를 n! 회만큼 반복하는 새로운 방법(그림 5)은 n이 아주 크지 않은 범위 내에서는 전체 실행 시간이 다른 기술(예. CPU 기반 또는 GPU tree 기반 검색 알고리즘)보다 빨라진다. 이에 비해서 기존 방식과 비교했을 때 정밀도가 상대적으로 크게 향상되는 장점을 얻을 수 있었다.
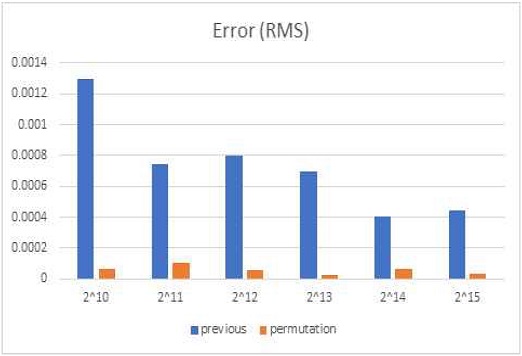
기존 방식과 제안하는 방식의 성능 비교를 위한 테스트 방식으로 3차원 공간 상에서 각각 데이터 벡터와 질의 벡터 개수를 210, 211, 212, 213, 214, 215으로 지정하고 무작위로 생성한 후 k=8에 대해 정확한 kNN (k-nearest neighbor)를 계산할 수 있는 kd-tree 검색 방식을 CPU에서 실행시킨 결과와 기존 방식(shifted-sorting 기반 kANN)과 제안하는 방식(permutation 적용 shifted-sorting 기반 kANN)을 실행한 후 실행 시간과 정확도를 계산하였다. 정확도를 확인하기 위해 kd-tree로 계산한 정확한 k개 최근접 이웃 데이터 벡터와의 Euclidean 거리와 기존 방식(shifted-sorting 기반 kANN) 및 제안하는 방식(permutation 적용 shifted-sorting 기반 kANN)으로 계산한 Euclidean 거리 사이의 평균 RMSE (Root Mean Square Error)으로 계산했다.
비교를 위하여 표 13에서 테스트 결과를 정리하였다.
표 1과 그림 6, 7, 8을 통해 제안하는 알고리즘의 특성을 확인할 수 있다. 먼저 제안하는 알고리즘은 허용 가능한 범위 내에서 계산 시간이 증가한다. 즉, 제안하는 방식은 3차원의 경우 3!=6배 많은 반복 루틴을 실행하나 대기 중의 작업 부하의 크기가 증가할수록 병렬 연산 효율이 증가하는 GPU의 하드웨어적인 측면 때문에 실행 시간은 정확하게 6배로 증가하지 않고 2.38배~4.2배 정도에 그치는 것을 볼 수 있다(표 1의 시간에 대한 Ⓑ/Ⓐ 비율 및 그림 6 참고). 제안하는 방식이 실행 시간이 최대 4배 정도 증가한다는 사실만 보면 실행 시간이 증가하더라도 데이터와 질의 개수가 각각 210개인 경우 0.55/0.0062 = 88.7배, 215개인 경우 23.73/0.045 = 527.3배로 연산 시간 측면에서 CPU 방식(kd-tree) 대비 상당히 빠른 속도라고 볼 수 있다(그림 7).
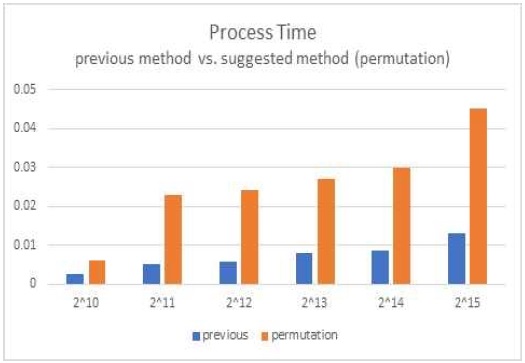
Process time comparison between the previous method and the suggest one (“permutation”) (unit: seconds)
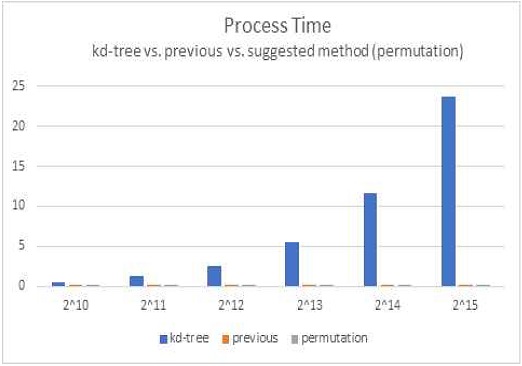
Process time comparison among CPU-based kd-tree, the previous method, and the suggest one (“permutation”) (unit: seconds)
앞서 논의한 대로 본 논문에서 다루는 근사 k개 최근접 검색(shifted sorting-based k-approximate nearest neighbor searching) 알고리즘은 각 질의 벡터에 대해 정확하게 가장 가까운 k개의 데이터 벡터를 찾는 것이 아니라 어느 정도의 오차를 허용하면서 근사적으로 가장 가까운 k개의 최근접 데이터 벡터를 찾는다. 다시 말해 본 논문에서 다루는 검색 알고리즘은 어느 정도의 정밀도를 희생하면서 속도 측면에서 상당한 장점을 얻기 위한 방법이다.
그림 6에서 제시한 것처럼 순열 순환을 적용하지 않은 기존 방법에 비해 제안하는 방법의 실행 시간은 최대 약 4배 정도 실행 시간의 증가가 있으나 그림 8에서 볼 수 있듯이 검색 오류(Root Mean Square Error, RMSE)가 크게 줄어드는 것을 볼 수 있다. 그림 8에서는 정확한 최근접 k개 점과 순열 순환을 적용하지 않은 기존 방법으로 찾은 방법 사이의 오류와 제안하는 방법의 오류를 비교한다. 그림 8에서 제시한 것처럼 간혹 예외가 있으나 제안하는 방법으로 찾은 근사 최근접점들의 대략적으로 약 10-2 정도의 order로 큰 폭으로 감소함을 볼 수 있다.
정리하면, 제안하는 방식은 어느 정도의 실행 시간 측면에서의 손해는 있으나 밀리세컨드 수준에서의 사소한 증가에 그치는 것에 비해서 근사 오차를 크게 감소시킨다고 결론 내릴 수 있다.
Ⅲ. 결 론
이동 정렬 기반 근사 k개 최근접 검색(shifted sorting-based k-approximate nearest neighbor searching) 알고리즘은 차원의 저주(the curse of dimensionality [9])로 인한 성능 저하를 극복하기 위해서 데이터와 질의가 포함된 다차원 벡터 공간을 Morton 코드로 변환하고 1차원으로 프로젝션함으로써 제한된 범위 내의 오차를 허용하면서 처리 속도 개선을 도모하는 방식이다.
본 논문에서는 어느 정도의 미미한 속도 저하를 희생하고 상대적으로 정밀도를 향상시킬 수 있는 방안을 제안한다. 논문에서 제시한 실험 결과에 따라 이러한 속도 저하는 정밀도의 향상에 비해 미미한 수준으로 볼 수 있다. 또한 본 논문에서 제안하는 순열을 선택적으로 적용한다면 애플리케이션에 따라 정밀도와 실행 시간의 트레이트오프(trade-off)를 제어할 수도 있다. 예를 들어 3차원 벡터 공간에 적용할 때 3!=6에 해당하는 모든 순열들을 적용하지 않고 일부(예를 들어 3개 조합만 선택)만 적용하면 6개를 적용해서 전체 루프를 적용하는 경우보다 RMS 오류는 증가하지만 실행 시간을 다소 줄일 수도 있다.
본 논문에서 제안하는 병렬 알고리즘은 고속 통계 분석, 기하 정보 처리, 기타 벡터 데이터의 클러스터링 처리 등 데이터 통계 처리 및 인공 지능 등의 기초를 이루는 루틴에 적용 가능한 기술로 활용성이 높다고 판단한다. 특히 4차산업혁명의 핵심적 요소라고 할 수 있는 CPS(Cyber-Physical System)의 운영을 위해 시뮬레이션 기반의 사이버 시스템이 효용성을 가지기 위해서는 이 사이버 시스템을 구성하는 소프트웨어 모듈의 고속 또는 실시간 처리가 필수적이며 이러한 여러 시뮬레이션에서 필수적인 연산으로 활용되는 클러스터링(clustering), 주변부 정보 검색에서 활용 가능한 원천 기술로 활용할 수 있는 기초적인 알고리즘으로 활용할 수 있으리라 생각한다.
Acknowledgments
본 연구는 덕성여자대학교 2019년도 교내연구비 지원에 의해 수행되었음.
References
- S. Li, L. Simons, J. B. Pakaravoor, F. Abbasinejad, J. D. Owens, and N. Amenta, “kANN on the GPU with shifted sorting,” In Proceedings of the Fourth ACM SIGGRAPH / Eurographics conference on High-Performance Graphics (EGGH-HPG'12), Switzerland, pp. 39-47, 2012.
- T. Mikolov, I. Sutskever, K. Chen, G. Corrado, and J. Dean, “Distributed representations of words and phrases and their compositionality,” In Proceedings of the 26th International Conference on Neural Information Processing Systems - Vol 2 (NIPS'13). Curran Associates Inc., Red Hook, NY, USA, pp. 3111–3119, 2013.
- T. Park, “Optimization of Warp-wide CUDA Implementation for Parallel Shifted Sort Algorithm,” Journal of Digital Contents Society, Vol. 18, No. 4, pp. 739-745, July 2017.
- H. Kim and T. Park, “Analysis of GPU-based Parallel Shifted Sort Algorithm by comparing with General GPU-based Tree Traversal,” Journal of Digital Contents Societ, Vol. 18, No. 6, pp. 1151-1156, October 2017.
-
T. M. Chan, “Approximate nearest neighbor queries revisited,” In Proceedings of the Thirteenth Annual Symposium on Computational Geometry (SCG ’97), New York, pp. 352–358, 1997.
[https://doi.org/10.1145/262839.263001]

-
T. Park, “Analysis of Morton Code Conversion for 32 Bit IEEE 754 Floating Point Variables,” The Journal of Digital Contents Society, Vol. 17, No. 3, pp. 165-172, June 2016.
[https://doi.org/10.9728/dcs.2016.17.3.165]

- J. Cheng, M. Grossman, and T. McKercher, “Unrolling Loops” in Chapter 3 CUDA Execution Model, Professional CUDA C Programming, 1st ed. Wrox, pp. 114-120, 2014.
- J. Cheng, M. Grossman, and T. McKercher, Chapter 3 CUDA Execution Model, Professional CUDA C Programming, 1st ed. Wrox, pp. 90-99, 2014.
- R. E. Bellman, Dynamic programming. Princeton University Press, 1957.
저자소개

1997년 : 서울대 전기공학부 (공학사)
1999년 : 서울대 전기공학부 대학원 (공학 석사, 반도체 물리 전공)
2006년 : 서울대 전기컴퓨터공학부 대학원 (공학박사, 컴퓨터 그래픽스 전공)
2018년~현재 : 덕성여자대학교 공과대학 사이버보안/IT미디어공학과 부교수
2013년~2017년 : 덕성여자대학교 정보미디어대학 디지털미디어학과 조교수
2006년~2013년 : 고려대학교 연구교수
※관심분야: 컴퓨터그래픽스, 병렬처리, 인공지능, 수치해석, 3차원 모델링