Optimal Shuffle을 적용한 HIGHT의 연관키 렉탱글 공격에 대한 안전성 분석

Ⅰ. 서 론

사물인터넷 (Internet of Things) 기술의 발달로 모바일, 센서 네트워크, RFID 등 다양한 분야가 함께 부상하고 있으며, 이를 위한 소형 컴퓨팅 장치가 보편화되고 있다. 해당 분야들은 사용자들에게 편리성과 유용성을 제공하기 위해 사용자들의 민감정보뿐 아니라 각종 생활 정보에 대한 빅데이터를 이용하므로 다양한 형태의 해킹 및 크래킹에 노출될 수 있다. 하지만 대부분의 소형화된 기기는 내부 자원이 제한적이므로 AES[1]와 같은 기존 블록 암호 알고리즘을 사용하기는 어려움이 있다. 따라서 이런 경량 환경에서 보안요소와 성능을 충족시키기 위한 다양한 경량 블록 암호 알고리즘이 제안되고 있다.

HIGHT (HIGh security and light weigHT)는 이러한 저전력, 경량화가 필요한 컴퓨팅 환경에서 기밀성을 제공하기 위해 국내에서 개발한 64-비트 블록 암호이며[2], 2006년 정보통신단체(TTA)의 표준으로 제정되었고[3], 2010년에 국제표준화기구(ISO/IEC) 18033-3의 표준으로 제정되었다[4]. HIGHT는 Generalized Feistel Network (GFN) 구조로 이루어져 있고, ARX (Addition-Rotation-XOR) 기반 8-비트 단위 연산을 진행한다.

현재까지 알려진 HIGHT에 대한 공격으로는 포화 공격, 불능 차분 공격, 연관키 불능 차분 공격, 바이클릭 공격(Biclique Attack), 연관키 렉탱글 공격이 있다. 구체적으로는 포화 공격을 이용한 22-라운드 공격[5], 불능 차분 공격을 이용한 26-라운드 공격[6], 연관키 불능 차분 공격을 이용한 31-라운드 공격[6], 바이클릭 공격을 이용한 전체 32-라운드 공격[7], 연관키 렉탱글 공격을 이용한 전체 32-라운드 공격이 제안되었다[8]. 바이클릭, 연관키 렉탱글 공격만이 HIGHT에 대한 전체 32-라운드 공격에 성공했고, 본 논문에서는 연관키 렉탱글 공격을 다룬다.

HIGHT에 대한 연관키 렉탱글 공격에서는 키 스케줄이 갖는 선형적 성질을 이용해 local collision을 발생시켜 distinguisher를 구성한다. 블록 암호에서 local collision은 어떤 서브키 차분에 의해 생긴 차분이 몇 라운드 후, 다른 서브키 차분에 의해 일정 확률로 상쇄되는 현상을 일컫는다. 연관키 차분을 이용하여 차분 경로를 구성하면 차분을 상쇄할 수 있으며, local collision 기법을 사용했을 때 이를 극대화할 수 있으므로 높은 확률의 긴 차분 경로를 효율적으로 구성할 수 있다.

본 논문의 구성은 다음과 같다. 2장에서는 기 제안된 HIGHT에 대한 전체 32-라운드 연관키 렉탱글 공격을 살펴본다. 3장에서는 HIGHT에 적용된 GFN 구조를 설명하고 8-branch GFN 구조가 가질 수 있는 최적 shuffle을 소개한다. 4장에서는 최적 shuffle을 적용한 HIGHT-variant에 대해서는 local collision 기법을 이용한 연관키 렉탱글 공격이 효과적이지 않음을 보인다. 마지막으로 5장에서는 본 논문에 대한 결론을 맺는다.

Ⅱ. 기 제안된 HIGHT에 대한 전체 라운드 연관키 렉탱글 공격

2004년 연관키 공격과 렉탱글 공격을 결합한 연관키 렉탱글 공격이 소개됐다[9]. 연관키 렉탱글 공격에서는 하나의 낮은 확률을 갖는 긴 연관키 차분 경로 대신 두 개의 높은 확률을 갖는 짧은 연관키 차분 경로를 이용한다. {0,1}ⁿ을 평문 또는 암호문 공간, {0,1}^k를 키 공간이라 할 때, 블록 암호 E : {0,1}ⁿ × {0,1}^k → {0,1}ⁿ를 두 sub-cipher E₀과 E₁의 연결이라 하자(E = E₁ ∘ E₀). 여기서 K는 임의의 키, ΔK₀와 ΔK₁는 연관키 차분, E_0,K(X)는 X를 키 K를 통해 E₀로 암호화하는 것을 의미한다. 이때, E₀, E₁의 연관키 차분 경로의 확률을 다음과 같이 정의한다.

연관키 렉탱글 공격은 두 sub-cipher의 연관키 차분 경로를 연결하여 distinguisher를 구성하며, 이 distinguisher를 만족하는 올바른 quartet의 기댓값을 고려한다. N개의 quartet이 생성됐을 경우, 올바른 quartet의 기댓값은 $$ N\cdot 2^{-n}\cdot {\widehat{p}}^2\cdot {\widehat{q}}^2$$이다. 반면, random cipher의 경우 올바른 quartet의 기댓값은 N ⋅2^-2n이 된다. 따라서 $$ \widehat{p}\cdot \widehat{q}>2^{-n/2}$$일 때 연관키 렉탱글 공격을 적용할 수 있다.

본 논문에서 사용하는 E₀, E₁의 연관키 차분 경로의 확률 $$ \widehat{p}$$, $$ \widehat{q}$$는 기존의 연관키 렉탱글 공격의 확률과 다소 다르다. 기존 연관키 렉탱글 공격에서는 $$ \widehat{q}$$의 확률 값으로 E₁에 대한 차분 특성과 연관키 차분 특성을 모두 고려했다. 하지만 [8]에서 제안한 공격에서는 연관키 차분이 있는 경우로 한정했으므로 본 논문에서도 해당 경우만 고려한다. 또한 기존의 확률에서는 평문, 암호문, 연관키에 대해 모두 XOR-차분인 경우를 고려하지만, 본 논문에서는 연관키에 대해서 법 2⁸에 대한 덧셈-차분을 고려한다. 따라서 ΔK₀, ΔK₁ 대신 Δ⁺K₀, Δ⁺K₁을 사용하며, E₀, E₁의 연관키 차분 경로 확률 $$ \widehat{p}$$, $$ \widehat{q}$$는 다음과 같이 변경된다.

본 장에서는 HIGHT 알고리즘과 키 스케줄에서 발견되는 선형적 성질을 설명한다. 그리고 ICISC 2010에서 Koo 등에 의해 제안된 HIGHT에 대한 24-라운드 연관키 렉탱글 distinguisher를 설명한다[8].

2-1 HIGHT Specification

HIGHT[2]는 64-비트 평문, 128-비트 키로부터 64-비트 암호문을 출력한다. 본 논문에서는 다음과 같은 표기법을 사용한다.

○ ⊕ : 배타적 논리합(XOR)
○ ⊞ : 법 2⁸ 덧셈(Addition modulo 2⁸)
○ ∥ : 연접
○ P, C : 64-비트 평문, 암호문
○ X_i : i 라운드 64-비트 중간값(0 ≤ i ≤32)
○ K : 128-비트 키
○ Δ : XOR-차분
○ Δ⁺ : 법 2⁸에 대한 덧셈-차분
○ WK[i] : 8-비트 화이트닝키(0 ≤ i ≤7)
○ SK[i] : 8-비트 서브키(0 ≤ i ≤127)
○ A^≪s : A의 s-비트 좌측 순환 이동

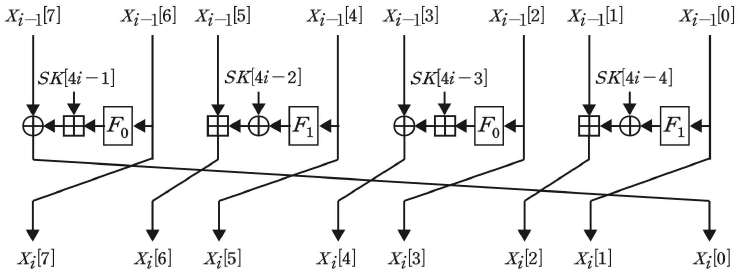
평문 P, 암호문 C, 중간값 X_i, 키 K는 다음과 같이 구성된다. 연접되는 각 요소는 모두 1-바이트이다.

$\[ \begin{array}{c}P=P\left[7\right]‖P\left[6\right]‖\cdots ‖P\left[0\right],\hfill \\ C=C\left[7\right]‖C\left[6\right]‖\cdots ‖C\left[0\right],\hfill \\ X_i=X_i\left[7\right]‖X_i\left[6\right]‖\cdots ‖X_i\left[0\right],\hfill \\ K=K\left[15\right]‖K\left[14\right]‖\cdots ‖K\left[0\right].\hfill \end{array} \]$

(3)

1) 키 스케줄

HIGHT의 키 스케줄은 먼저 128-비트 키로부터 초기 변환과 최종 변환에 쓰이는 8개의 8-비트 화이트닝키를 생성한다.

$\[ \begin{array}{c}WK\left[i\right]\leftarrow K\left[i+12\right] \left(0\le i\le 3\right)\hfill \\ WK\left[i\right]\leftarrow K\left[i-4\right] \left(4\le i\le 7\right).\hfill \end{array} \]$

(4)

그 후, 키로부터 각 라운드에서 사용하는 128개의 8-비트 서브키를 생성한다.

$\[ \begin{array}{c}for i=0 to 7\hfill \\ for j=0 to 7\hfill \\ SK\left[16i+j\right]\leftarrow K\left[j-i \text{mod} 8\right]⊞\delta \left[16i+j\right]\hfill \\ \hfill \\ \begin{array}{c} for j=0 to 7\hfill \\ SK\left[16i+j+8\right]\leftarrow K\left[\left(j-i \text{mod} 8\right)+8\right]⊞\delta \left[16i+j+8\right]\hfill \end{array}\hfill \end{array} \]$

(5)

여기서 δ[i](0 ≤ i ≤127)는 LFSR(Linear Feedback Shift Register)을 이용하여 생성하는 8-비트 상수이다.

2) 암호화 과정

HIGHT의 암호화 과정은 다음과 같은 초기 변환 과정으로부터 시작된다.

$\[ \begin{array}{c}{X}_0\left[0\right]\leftarrow P\left[0\right]⊞WK\left[0\right];X_0\left[2\right]\leftarrow P\left[2\right]\oplus WK\left[1\right];\hfill \\ X_0\left[4\right]\leftarrow P\left[4\right]⊞WK\left[2\right];X_0\left[6\right]\leftarrow P\left[6\right]\oplus WK\left[3\right];\hfill \\ X_0\left[1\right]\leftarrow P\left[1\right];X_0\left[3\right]\leftarrow P\left[3\right];\hfill \\ X_0\left[5\right]\leftarrow P\left[5\right];X_0\left[7\right]\leftarrow P\left[7\right].\hfill \end{array} \]$

(6)

HIGHT의 라운드 함수는 아래의 식과 같으며, i = 1, ⋯, 32에 대하여 동작한다.(그림 1)

Fig. 1.

Round functions of HIGHT(Type-Ⅱ)

$\[ \begin{array}{c}{X}_i\left[0\right]\leftarrow X_{i-1}\left[7\right]⨁\left(F_0\left(X_{i-1}\left[6\right]\right)⊞SK\left[4i-1\right]\right);\hfill \\ X_i\left[2\right]\leftarrow X_{i-1}\left[1\right]⊞\left(F_1\left(X_{i-1}\left[0\right]\right)⨁SK\left[4i-2\right]\right);\hfill \\ X_i\left[4\right]\leftarrow X_{i-1}\left[3\right]⨁\left(F_0\left(X_{i-1}\left[2\right]\right)⊞SK\left[4i-3\right]\right);\hfill \\ X_i\left[6\right]\leftarrow X_{i-1}\left[5\right]⊞\left(F_1\left(X_{i-1}\left[4\right]\right)⨁SK\left[4i-4\right]\right);\hfill \\ X_i\left[1\right]\leftarrow X_{i-1}\left[0\right];X_i\left[3\right]\leftarrow X_{i-1}\left[2\right];\hfill \\ X_i\left[5\right]\leftarrow X_{i-1}\left[4\right];X_i\left[7\right]\leftarrow X_{i-1}\left[6\right].\hfill \end{array} \]$

(7)

여기서 F₀과 F₁은 좌측 순환 이동과 XOR을 사용한 함수이다.

$\[ \left\{\begin{array}{c}{F}_0\left(0\right)=x^{\ll 1}⨁x^{\ll 2}⨁x^{\ll 7}\hfill \\ F_1\left(0\right)=x^{\ll 3}⨁x^{\ll 4}⨁x^{\ll 6}.\hfill \end{array}\right. \]$

(8)

HIGHT 암호화 과정의 마지막인 최종 변환 과정은 다음과 같다.

$\[ \begin{array}{c}C\left[0\right]\leftarrow X_{32}\left[1\right]⊞WK\left[4\right];C\left[2\right]\leftarrow X_{32}\left[3\right]\oplus WK\left[5\right];\hfill \\ C\left[4\right]\leftarrow X_{32}\left[5\right]⊞WK\left[6\right];C\left[6\right]\leftarrow X_{32}\left[7\right]\oplus WK\left[7\right];\hfill \\ C\left[1\right]\leftarrow X_{32}\left[2\right];C\left[3\right]\leftarrow X_{32}\left[4\right];\hfill \\ C\left[5\right]\leftarrow X_{32}\left[6\right];C\left[7\right]\leftarrow X_{32}\left[0\right].\hfill \end{array} \]$

(9)

2-3 HIGHT의 24-라운드 연관키 렉탱글 distinguisher

[8]에서는 확률 2^-117.68을 갖는 24-라운드 연관키 렉탱글 distinguisher를 구성하고 이를 통해 전체 32-라운드 HIGHT에 대한 공격을 제안한다. distinguisher는 E₀의 8.5-라운드 연관키 부정 차분 경로와 E₁의 15.5-라운드 연관키 부정 차분 경로로 구성되며, 두 경로의 연결 부분에는 ladder switch 기법[10]이 적용되었다.

E₀의 8.5-라운드 연관키 차분 경로는 [11][12]에서 제시한 경로에 기반을 두고 있으며, 확률은 2^-12.017보다 크다. E₀의 연관키 차분 경로는 (11)과 같다

$\[ \begin{array}{c}\left(0x\mathrm{00,0}x00,A,0x\mathrm{80,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x00\right)\hfill \\ \to \left(0x\mathrm{00,0}x\mathrm{00,0}x00,B,0x\mathrm{80,0}x\mathrm{00,0}x\mathrm{00,0}x00\right)\end{array} \]$

(11)

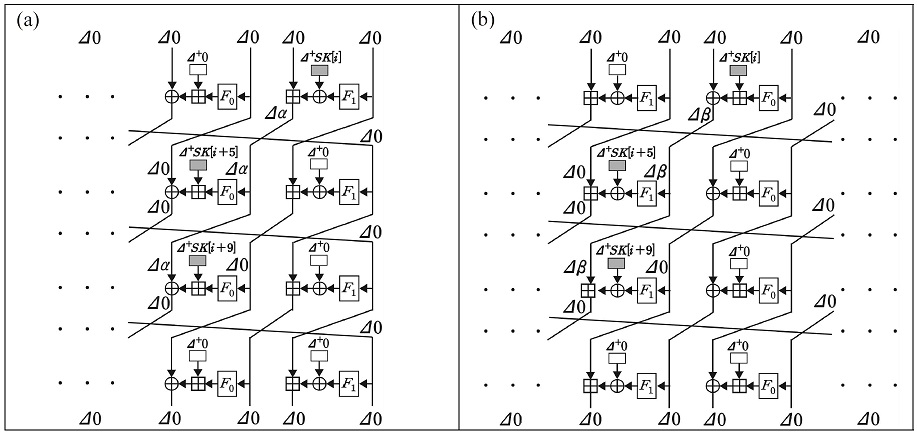
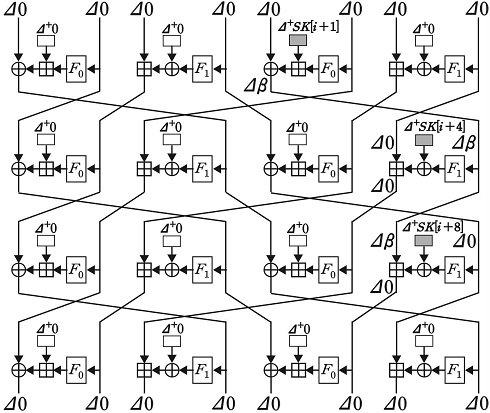
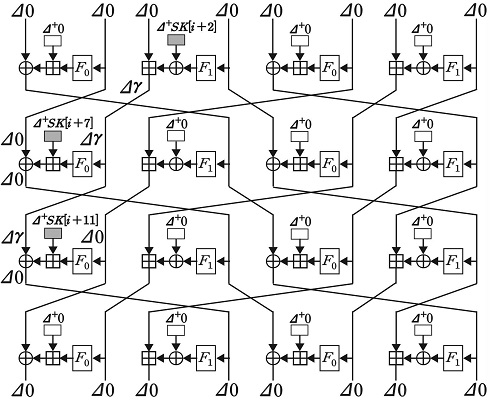
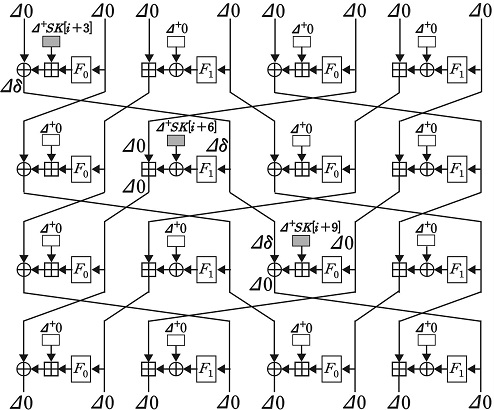
E₁의 15.5-라운드 연관키 차분 경로는 Type A, Type B 두 가지 4-라운드 local collision을 반복 적용하여 구성한다(그림 2). Type A는 XOR, 법 2⁸에 대한 덧셈 순서로 연산하는 branch, Type B는 법 2⁸에 대한 덧셈, XOR 순서로 연산하는 branch에 Δ⁺SK[i]을 준다. 따라서 Δ⁺SK[i+5], Δ⁺SK[i+9]도 Type에 따라 다른 연산 순서를 갖는 branch에 주게 된다. [8]에서는 K[1], K[5], K[9]에 각각 0x10, 0x68, 0x10의 덧셈 차분을 주고 두 local collision의 lower bound를 구한다. 이때 Type A local collision은 Δα의 값이 0x10 또는 0x30일 때만 발생하며, Type B local collision은 Δβ의 값이 0x70이고 Sk[82] = 0b ???1 1???일 때만 발생한다(?는 0 또는 1). 연관키 차분 관계는 식 (12)와 같다.

Fig. 2.

Local collisions in HIGHT. (a) Type A local collision (b) Type B local collision

$\[ \begin{array}{c}{\Delta }^{+}K\left[1\right]={\Delta }^{+}SK\left[69\right]={\Delta }^{+}SK\left[86\right]={\Delta }^{+}SK\left[103\right]\hfill \\ {\Delta }^{+}K\left[5\right]={\Delta }^{+}SK\left[65\right]={\Delta }^{+}SK\left[82\right]={\Delta }^{+}SK\left[99\right]\hfill \\ {\Delta }^{+}K\left[9\right]={\Delta }^{+}SK\left[60\right]={\Delta }^{+}SK\left[77\right]={\Delta }^{+}SK\left[94\right]\hfill \end{array} \]$

(12)

16~19-라운드에 Type A, 20~23-라운드에 Type B, 24~27-라운드에 Type A local collision을 적용했다. E₁의 연관키 차분 경로는 (13)과 같다.

$\[ \begin{array}{c}\left(0x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x00,C\right)\hfill \\ \to \left(0x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x\mathrm{00,0}x00\right)\end{array} \]$

(13)

C 부분에는 총 4개의 값을 고려할 수 있으며, 경로의 확률은 2^-41.661보다 크다.

Ⅲ. GFN 구조

본 장에서는 HIGHT 알고리즘에 쓰인 GFN 구조에 대해 설명한다. 또한 8-branch GFN Type-Ⅱ 구조에 대한 최적의 shuffle을 제시한다.

3-2 8-branch에 대한 최적의 shuffle

[15]에서는 전수조사를 통해 8-branch GFN 구조에서 가장 안전성이 높은 No.1 shuffle과 De Bruijn graph를 이용해 찾은 또 다른 No.2 shuffle을 제시한다(표 1).

Table 1.

Optimum Block Shuffles(8-branch)

표 1에서 D는 최소 확산 라운드, IDC는 불능 차분 경로의 최대 라운드, SC는 포화 공격의 최대 라운드, AS_D는 20-라운드 차분 공격(DC)에 대한 최소 active S-box의 개수, AS_L는 20-라운드 선형 공격(LC)에 대한 최소 active S-box의 개수를 의미한다.

D가 작을수록 더 빠르고 효율적인 차분의 확산이 일어나며, IDC와 SC가 작을수록 구성할 수 있는 distinguisher가 짧아지므로 전체 cipher에 대한 공격이 어려워진다. AS_D, AS_L가 커지면 고려해야 하는 확률의 개수가 많아져 DC distinguisher와 LC distinguisher가 짧아지므로 공격이 어려워진다.

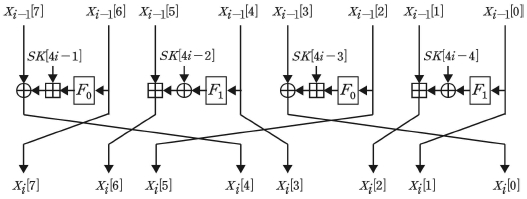
Nyberg의 shuffle은 기존의 Type-Ⅱ shuffle보다 IDC, SC 관점에서는 향상됐지만, DC, LC 관점에서는 더 취약해졌다. No.1, No.2 shuffle은 Nyberg의 shuffle보다 여러 측면에서 향상됐다. De Bruijn graph를 통해 제시한 No.2 shuffle은 No.1 shuffle보다 IDC 관점에서는 안전하지만, DC, LC 관점에서는 더 취약하다. 따라서 본 논문에서는 No.1 shuffle을 HIGHT의 최적 shuffle로 정의하며, 최적 shuffle을 적용한 HIGHT의 라운드 함수는 그림 3과 같다.

Fig. 3.

Round functions of HIGHT-variant(No.1)

Ⅳ. 최적 shuffle이 적용된 HIGHT-variant에 대한 기존 연관키 렉탱글 공격의 적용 가능성

본 장에서는 HIGHT의 기존 shuffle을 최적 shuffle로 바꾼 HIGHT-variant를 고려한다. 또한 HIGHT-variant에서 관찰할 수 있는 local collision들을 제시하고, 2.3절과 같은 방식으로 local collision의 반복 교차 적용을 통해 연관키 차분 경로를 구성할 수 있는지 분석한다. 마지막으로 구체적인 distinguisher를 제시하여 HIGHT-variant에서는 연관키 렉탱글 공격을 통한 전체 32-라운드 공격을 방지할 수 있음을 밝힌다.

4-1 HIGHT-variant에서 관찰할 수 있는 4-라운드 local collisions

HIGHT의 shuffle은 규칙적인 단순 회전 시프트이므로 각 라운드 함수의 XOR과 법 2⁸에 대한 덧셈 순서만 고려하면 다른 local collision을 구성할 수 있었다. 하지만 HIGHT-variant의 shuffle은 주목할만한 규칙성이 없으므로 한 라운드 함수에 연관키 차분을 줬을 때 기존보다 다양한 양상으로 차분이 퍼지게 된다. 따라서 HIGHT-variant에서는 어떤 branch에 연관키 차분을 주는지에 따라 4가지의 local collision을 관찰할 수 있다.

1) Type A

X_i[0]과 X_i[1]이 연산 되는 라운드 함수에 연관키 차분을 주는 경우 그림 4와 같은 Type A local collision을 관찰할 수 있다.

Fig. 4.

Type A local collision in HIGHT-variant

2) Type B

X_i[2]와 X_i[3]가 연산 되는 라운드 함수에 연관키 차분을 주는 경우 그림 5와 같은 Type B local collision을 관찰할 수 있다.

Fig. 5.

Type B local collision in HIGHT-variant

3) Type C

X_i[4]와 X_i[5]가 연산 되는 라운드 함수에 연관키 차분을 주는 경우 그림 6과 같은 Type C local collision을 관찰할 수 있다.

Fig. 6.

Type C local collision in HIGHT-variant

4) Type D

X_i[6]와 X_i[7]가 연산 되는 라운드 함수에 연관키 차분을 주는 경우 그림 7과 같은 Type D local collision을 관찰할 수 있다.

Fig. 7.

Type D local collision in HIGHT-variant

4-2 4-라운드 local collision의 반복 적용을 통한 E₁의 연관키 차분 경로의 구성 가능성

본 절에서는 HIGHT-variant에 대해 2.3절과 같이 local collision을 반복 적용하여 E₁의 연관키 차분 경로를 구성할 수 있는지 분석한다. 특히 반복 적용이 가능한 연관키 차분을 생성하더라도 유의미한 횟수만큼 반복하기 위해서는 그 경로의 차분 확률이 충분히 높아야 한다. 따라서 Type A, B, C, D와 같이 차분이 시작되는 라운드의 연관키 차분이 한 바이트에만 주어지는 반복 차분 경로만을 고려한다.

첫 local collision을 Type A로 선택하고 뒤에 또 다른 local collision을 적용하여 distinguisher를 구성하는 과정을 생각해보자. 이때, 연관키 차분은 첫 local collision 경로를 따라 주어져야 한다. 따라서 식 (14)와 같은 연관키 차분을 생각할 수 있다.

$\[ \begin{array}{c}{\Delta }^{+}K\left[j_1\right]={\Delta }^{+}SK\left[i\right]={\Delta }^{+}SK\left[i+17\right]\hfill \\ ={\Delta }^{+}SK\left[i+34\right]\hfill \\ \begin{array}{c}{\Delta }^{+}K\left[j_2\right]={\Delta }^{+}SK\left[i+5\right]={\Delta }^{+}SK\left[i+22\right]\hfill \\ ={\Delta }^{+}SK\left[i+39\right]\hfill \end{array}\hfill \\ \begin{array}{c}{\Delta }^{+}K\left[j_3\right]={\Delta }^{+}SK\left[i+10\right]={\Delta }^{+}SK\left[i+27\right]\hfill \end{array}\hfill \end{array} \]$

(14)

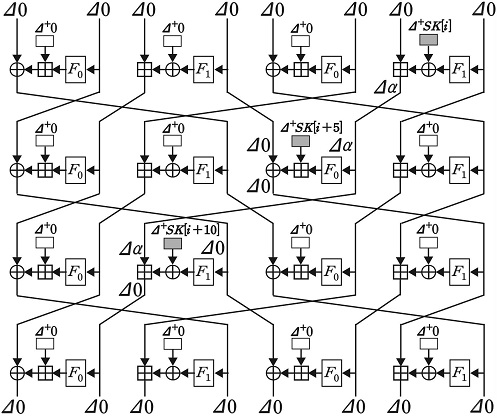
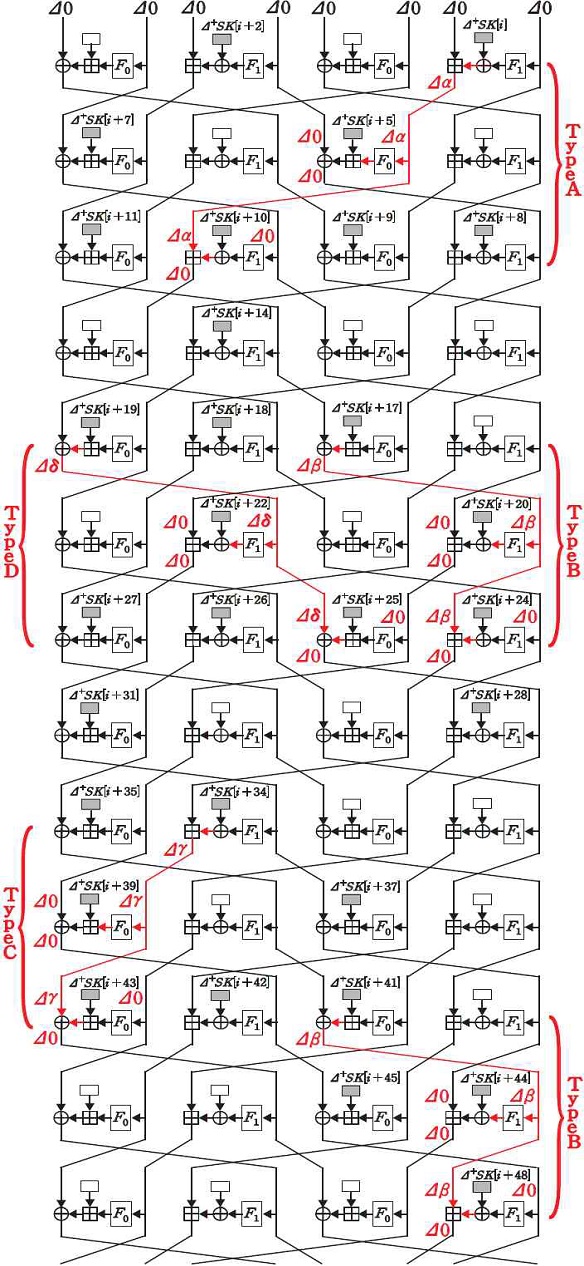
같은 Type의 local collision을 두 번 연속적으로 적용할 수 있는지 확인하기 위해 위 수식과 같이 처음 경로에 Type A local collision이 발생했다고 가정하자. 두 번째 local collision에도 Type A local collision을 발생시키기 위해서는 해당 local collision의 경로가 Δ⁺SK[i+17], Δ⁺SK[i+22], Δ⁺SK[i+27] 연관키 차분이 발생하는 경로와 일치해야 한다. 그러나 바뀐 shuffle을 고려했을 때 해당 상황은 불가능하다. 따라서 HIGHT-variant에서는 Type A local collision를 연속적으로 적용하여 8-라운드 distinguisher를 구성할 수 없다(그림 8).

Fig. 8.

Infeasibility of local collisions in 13-round HIGHT-variant

다른 Type의 local collision을 두 번 연속적으로 적용할 수 있는지 확인하기 위해 이전 방법과 같이 첫 번째 local collision은 Type A, 두 번째는 Type B를 적용한다고 하자. 이때 Type B와 같은 local collision이 발생하기 위해서는 SK[i+20], SK[i+24]에 연관키 차분이 추가적으로 주어져야 한다. 이것은 키 스케줄의 의해 Δ⁺SK[i+7], Δ⁺SK[i+11], Δ⁺SK[i+37], Δ⁺SK[i+41] 연관키 차분도 주어진다는 것을 의미한다. 유사한 방식으로 연관키 차분을 반복 적용하기 위해서 총 10-바이트의 연관키 차분이 추가로 주어진다. 이때 13-라운드를 기준으로 최소 Type A가 1번, Type B가 2번, Type C가 1번. Type D가 1번 발생하게 되며, 그 외 상쇄되지 않는 연관키 차분도 존재하게 된다(그림 8).

구체적으로 다른 Type의 local collision이 두 번 연속적으로 적용되는 경우에 대해 E₁의 13-라운드 연관키 차분 경로가 가지는 확률 upper bound를 구해보자. 관련 컴퓨터 계산을 통해 HIGHT-variant에서 관찰할 수 있는 Type A, Type B, Type C, Type D의 확률 upper bound를 계산했으며, 내용은 표 2와 같다.

Table 2.

Upper bounds of probability of 4-round local collisions in HIGHT-variant

local collision만을 고려한 E₁의 두 연관키 차분 경로의 확률 $$ {\widehat{q}}^2$$는 다음과 같이 계산된다.

(15)

HIGHT-variant의 shuffle을 고려하여 변경된 E₀의 8.5-라운드 연관키 차분 경로와 그림 8과 같은 E₁의 연관키 차분 경로를 고려하자. ladder switch 기법을 고려하면 두 경로를 통해 23-라운드 연관키 렉탱글 distinguisher를 구성할 수 있다. E₀의 두 연관키 차분 경로의 확률 $$ {\widehat{p}}^2$$는 를 만족하고, E₁의 두 연관키 차분 경로의 확률 $$ {\widehat{q}}^2$$의 upper bound를 알고 있으므로 23-라운드 연관키 렉탱글 distinguisher의 확률은 가 성립함을 알 수 있다. E₁의 연관키 차분 경로의 첫 local collision이 다른 Type인 경우에 대한 $$ {\widehat{p}}^2\cdot {\widehat{q}}^2$$의 upper bound는 표 3와 같다. 따라서 기존의 4-라운드 local collision을 반복 적용하는 방식으로는 E₁의 효과적인 연관키 차분 경로를 구성할 수 없다는 것을 알 수 있다.

Table 3.

Upper bounds of probability of 23-round related-key distinguisher

4-3 HIGHT-variant의 연관키 렉탱글 공격 distinguisher

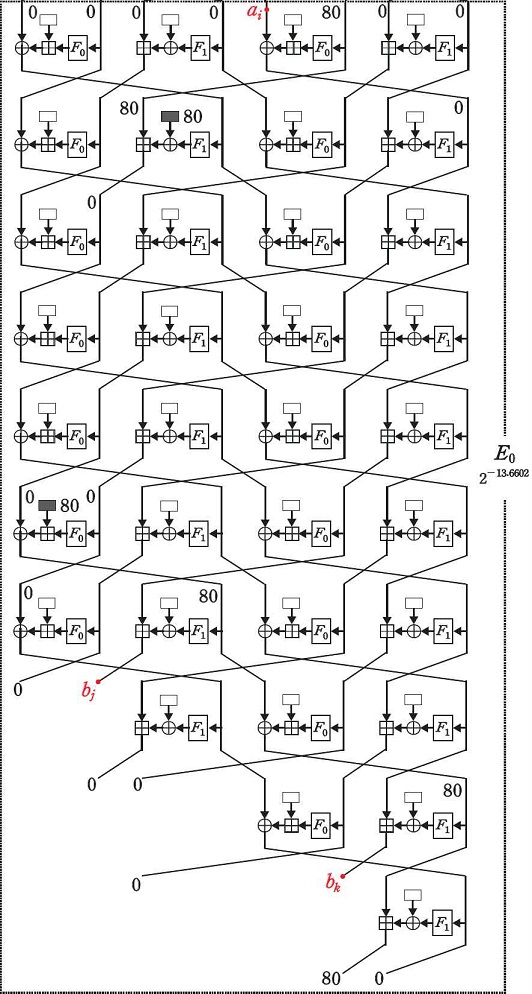
그림 9과 그림 10은 HIGHT-variant에 대해 본 논문에서 제시하는 E₀, E₁의 연관키 차분 경로이며, 이를 통해 15-라운드 연관키 렉탱글 distinguisher를 구성할 수 있다. E₀의 연관키 차분 경로는 [8][11][12]에서 사용한 경로 구성을 본 셔플에 적합하게 응용하여 기존과 동일한 라운드 수를 가지며, 키 복구 공격을 고려하여 4라운드에서 시작한다. 또한 높은 확률의 긴 차분 경로를 구성하기 위해 부정 차분과 ladder switch 기법을 적용했다.

Fig. 9.

8.5-round Related-key differential trail for E0 in HIGHT-variant

Fig. 10.

6.5-round Related-key differential trail for E1 in HIGHT-variant

E₁의 높은 확률을 갖는 긴 연관키 차분 경로를 찾기 위해 SAT Solver¹⁾를 사용했으며, Espresso 알고리즘 사용해서 HIGHT의 법 2⁸ 덧셈 제약식을 56개로 축소하여 조사의 효율성을 높였다[17]. 만약 local collision이 4번 이상 발생하고 E₁ 경로의 입력, 출력 바이트에 연관키에 따른 부정 차분을 고려해야 한다면 표 2의 확률을 고려할 때 연관키 렉탱글 공격을 위한 확률 수치를 만족할 수 없다. 따라서 최대 3번의 local collision을 가지면서 local collision 이외의 연관키 차분은 존재하지 않고 최대 라운드를 갖는 경로를 조사했다. 결과적으로 7라운드 이상 길이를 갖는 E₁의 연관키 차분 경로는 구성할 수 없음을 알 수 있었다. 따라서 본 절에서 제시하는 distinguisher와 같이, HIGHT-variant에 대해 기대할 수 있는 local collision을 이용한 연관키 렉탱글 공격 최대 라운드 수는 15라운드이다.

E₀, E₁의 연관키 차분 경로에 대한 입력, 출력 바이트와 해당 차분 값은 표 4와 같으며 차분 집합 ΔA, ΔB, ΔC은 다음과 같이 16진수 값의 집합 표현으로 정의한다.

Table 4.

Byte positions and differences both inputs and outputs for distinguishers of E0 and E1

$\[ \begin{array}{c}\Delta \text{A}=\left\{\mathrm{41,43},c1,c3\right\},\hfill \\ \Delta \text{B}=\left\{\mathrm{14,1}c,\mathrm{24,2}c,\mathrm{34,3}c,\mathrm{54,5}c,\mathrm{64,6}c,\mathrm{74,7}c,d4,dc,e4,ec,f4,fc\right\},\hfill \\ \Delta \text{C}=\left\{\mathrm{68,87,98},a8,b8,e8,f8\right\}.\hfill \end{array} \]$

(16)

1) E₀의 연관키 차분 경로의 확률

E₀의 두 연관키 차분 경로의 확률을 구하기 위해서는 ΔX₄[0], ΔX₁₀[6], ΔX₁₂[2]의 값을 분석할 필요가 있다. 따라서 모든 a_i∈ΔA(0 ≤ i ≤ 3), b_j, b_k∈ΔB(0 ≤ j,k ≤ 17)에 대하여 확률 u_i, v_j, v_k를 다음과 같이 정의한다.

$\[ \begin{array}{c}{u}_i≔\text{P}\left[\Delta X_4\left[0\right]=0\left|\Delta X_3\left[3\right]=a_i\right.\right]\times \text{P}\left[\Delta X_3\left[3\right]=a_i\right]\hfill \\ v_j≔\text{P}\left[\Delta X_{10}\left[6\right]=b_j\right]\hfill \\ v_k≔\text{P}\left[\Delta X_{12}\left[2\right]=b_k\right]\hfill \end{array} \]$

(17)

이때 E₀의 두 연관키 차분 경로의 확률 $$ {\widehat{p}}^2$$는 다음과 같이 계산된다.

$\[ \begin{array}{c}{\widehat{p}}^2={\left(\sum _{i=0}^3{u}_i\right)}^2\cdot \sum _{j=0}^{17}{v}_j^2\cdot \sum _{k=0}^{17}{v}_k^2\hfill \\ \ge 2^{-6}\times 2^{-3.83007}\times 2^{-3.83007}\hfill \\ >2^{-13.6602}\hfill \end{array} \]$

(18)

2) E₁의 연관키 차분 경로의 확률

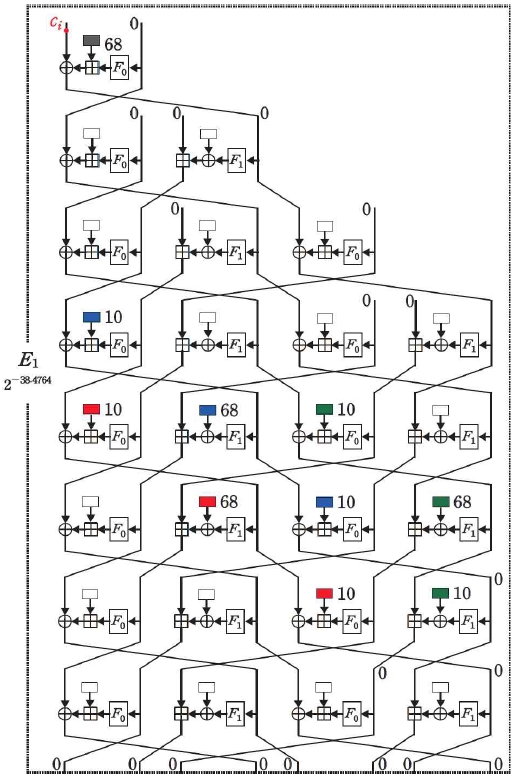
E₁의 두 연관키 차분 경로의 확률을 구하기 위해서는 ΔX₁₁[4] 부분과 local collision 발생 시 고려해야 하는 확률을 종합적으로 분석해야 한다. 본 경로에서는 14~16, 15~17라운드에서 Type D, 15~17라운드에서 Type B local collision을 발생시킨다. 모든 c_i∈ΔC (0 ≤ i ≤ 6)에 대하여 확률 w_i, q_l를 다음과 같이 정의한다.

$\[ \begin{array}{c}{w}_i≔\text{P}\left[\Delta X_{11}\left[4\right]=0\left|\Delta X_{10}\left[7\right]=c_i\right.\right]\hfill \\ q_l≔\text{local collision에 의한 14~17라운드 연관키 차분 경로}\hfill \end{array} \]$

(19)

이때 E₁의 두 연관키 차분 경로의 확률 $$ {\widehat{q}}^2$$는 다음과 같이 계산된다.

$\[ \begin{array}{c}{\widehat{q}}^2=\sum _{i=0}^6{w}_i^2\cdot q_l^2\hfill \\ \ge 2^{-2.47643}\times 2^{-36}\hfill \\ >2^{-38.4764}\hfill \end{array} \]$

(20)

3) 전체 distinguisher의 확률

E₀의 8.5-라운드 연관키 차분 경로와 E₁의 6.5-라운드 연관키 차분 경로를 통해 15-라운드 연관키 렉탱글 공격 distinguisher를 구성할 수 있으며 해당 distinguisher의 확률 lower bound는 다음과 같이 계산된다.

$\[ \begin{array}{c}{\widehat{p}}^2\cdot 2^{-64}\cdot {\widehat{q}}^2>2^{-13.6602-64-38.4764}\\ =2^{-116.1366}\\ >2^{-116.136}\end{array} \]$

(21)

따라서 2^118.136개의 quartet을 생성하면 키 복구 공격이 가능하다. 하지만 HIGHT의 전체 라운드 수는 32라운드이므로, 위의 15라운드 distinguisher를 이용한 전체 라운드 키 복구 공격으로의 확장은 불가능하다.

Ⅴ. 결 론

본 논문에서는 HIGHT의 GFN 구조에 최적 shuffle을 적용한 HIGHT-variant를 제안했다. HIGHT-variant에서는 4-라운드 local collision을 반복 적용하는 방식으로 효과적인 연관키 차분 경로를 구성할 수 없었다(표 5).

Table 5.

Total summary

또한 2^-116.136의 확률을 갖는 15-라운드 연관키 렉탱글 공격 distinguisher를 구성했다. 하지만 전체 라운드 공격을 위해서는 부족함을 알 수 있었는데, 이는 최적 shuffle로 인하여 반복적인 local collision 경로를 구성하기 어려운 점에 기인한다. 따라서 HIGHT에 최적 shuffle을 적용했을 때 local collision 기법을 이용한 전체 라운드 연관키 렉탱글 공격을 방지할 수 있어, 안전성이 향상될 수 있음을 알 수 있었다.

GFN 구조는 확산이 느리다는 단점이 있으나 이를 향상시키기 위한 연구는 지속해서 진행되고 있으며, 최신 관련 연구에서 branch 수에 따른 최적 shuffle을 제시하고 있다[18]. 본 논문에서 제시한 바와 같이 최적 shuffle을 암호 알고리즘에 적용했을 때 기존보다 향상된 안전성을 기대할 수 있고, 암호 설계자의 입장에서는 더 적은 라운드 수를 사용하여 암호의 성능을 향상시킬 수 있다. 따라서 GFN 구조를 갖는 기존 암호 알고리즘들에 대해 최적 shuffle을 적용한 후 차분, 선형 공격 등 여러 공격에 대한 안전성 연구를 수행할 필요가 있다.

Acknowledgments

본 연구는 고려대 암호기술 특화연구센터(UD170109ED)를 통한 방위사업청과 국방과학연구소의 연구비 지원으로 수행되었습니다.

참고문헌

• NIST, “Advanced Encryption Standard,” FIPS-197, Nov. 2001. [https://doi.org/10.1016/S1353-4858(01)01018-2]
• Deukjo Hong, Jaechul Sung, Seokhie Hong, Jongin Lim, Sangjin Lee, Bon-Seok Koo, Changhoon Lee, Donghoon Chang, Jesang Lee, Kitae Jeong, Hyun Kim, Jongsung Kim and Seongtaek Chee, “HIGHT: A New Block Cipher Suitable for Low-Resource Device,” CHES’06, LNCS 4249, pp. 46-59, Oct. 2006. [https://doi.org/10.1007/11894063_4]
• Telecommunications Technology Association, “TTAK.KO-12.0040/R1(revised),” TTAS, 2008.
• International Organization for Standadization, “ISO/IEC 18033-3:2010,” ISO/IEC 18033-3, 2010.
• Peng Zhang, Bing sun and Chao Li, “Saturation Attack on the Block Cipher HIGHT,” CANS’09, LNCS 5888, pp. 76-86, Dec. 2009. [https://doi.org/10.1007/978-3-642-10433-6_6]
• Onur Özen, Kerem Varıcı, Cihangir Tezcan and Çelebi Kocair, “Lightweight Block Ciphers Revisited: Cryptanalysis of Reduced Round PRESENT and HIGHT,” ACISP’09, LNCS 5594, pp. 90-107, Jul. 2009. [https://doi.org/10.1007/978-3-642-02620-1_7]
• Deukjo Hong, Bonwook Koo, Daesun kwon, “Biclique Attack on the Full HIGHT,” ICISC’11, pp. 365-374, Nov. 2011. [https://doi.org/10.1007/978-3-642-31912-9_24]
• Bonwook Koo, Deukjo Hong and Daesung Kwon, “Related-Key Attack on the Full HIGHT,” ICISC’10, pp. 49-67, Dec. 2010.
• Jongsung Kim, Guil Kim, Seokhie Hong, Sangjin Lee and Dowon Hong, “The Related-Key Rectangle Attack – Application to SHACAL-1,” ACISP’04, LNCS 3108, pp. 123-136, Jul. 2004. [https://doi.org/10.1007/978-3-540-27800-9_11]
• Alex Biryukov and Dmitry Khovratovich, “Related-key Cryptanalysis of the Full AES-192 and AES-256,” ASIACRYPT’09, LNCS 5912, pp. 1-18, 2009. [https://doi.org/10.1007/978-3-642-10366-7_1]
• Jiqiang Lu, “Cryptanalysis of reduced versions of the HIGHT block cipher from CHES 2006,” ICISC’07, pp. 11-26, 2007.
• Jiqiang Lu, “Cryptanalysis of Block Ciphers,” Ph.D. Thesis, Royal Holloway, University of London, Jul. 2008.
• Yuliang Zheng, Tsutomu Matsumoto and Hideki Imai, “On the Construction of Block Ciphers Provably Secure and Not Relying on Any Unproved Hypotheses,” CRYPTO’89, LNCS 435, pp. 461-480, 1989. [https://doi.org/10.1007/0-387-34805-0_42]
• Kaisa Nyberg, “Generalized Feistel Networks,” ASIACRYPT’96, LNCS 1163, pp. 91-104, 1996. [https://doi.org/10.1007/BFb0034838]
• Tomoyasu Suzaki and Kazuhiko Minematsu, “Improving the Generalized Feistel,” FSE’10, LNCS 6147, pp. 19-39, 2010. [https://doi.org/10.1007/978-3-642-13858-4_2]
• Mate Soos, Karsten Nohl and Claude Castelluccia, “Extending SAT Solvers to Cryptographic Problems,” SAT’09, LNCS 5584, pp. 244-257, 2009. [https://doi.org/10.1007/978-3-642-02777-2_24]
• Robert K. Brayton, Gary D. Hachtel, Curtis T. Mcmullen and Alberto L. Sangiovanni-vincentelli, “Logic Minimization Algorithms for VLSI Synthesis,” Springer Science & Business Media, Vol. 2. 1984. [https://doi.org/10.1007/978-1-4613-2821-6]
• Patrick Derbez, Pierre-Alain Fouque, Baptiste Lambin and Victor Mollimard, “Efficient Search for Optimal Diffusion Layers of Generalized Feistel Networks,” IACR Transactions on Symmetric Cryptology, pp. 218-240, 2019.