Probabilistic Bloom Filter for Online Learning in Personalized Recommender Systems

Ⅰ. Introduction

In machine learning domain, the importance of online learning is growing. Although cloud environment to deal with big data is rising, there is a limit to data digestion capacity and it is still painful to use large batch data for training at once. Online learning can reduce the pain by using a handful of data each time. While online learning has the property to make big data manageable, it is also important to quickly reflect the concept drift.

The importance of embedding is also growing. In domains with a large users and items, how to reduce dimensions is an important issue in modeling. Bloom filters are emerging as storage saving[1] and embeddings in machine learning domain, especially in recommender systems[2][3][4].

In online learning environment, since new data keeps coming in, there is a need to reset the existing cells of a bloom filter in order to prevent bloom filters becoming full, and there are some algorithms related to it. However, there is no comparison as to what characteristics each algorithm shows in the online learning environment.

In this paper, we propose a new decay bloom filter which has a different characteristic and compare algorithms in online learning situation of a recommender system.

Ⅱ. Related Work

Stable bloom filter[5] sets cell values as a predefined max cell value when inserting an item. When decaying, it decreases 1 on randomly selected cells. It provides an algorithm to decide the number of cells to be randomly chosen where a target false positive rate, a dimension of bloom filter, and a max cell value are given. This makes it easier to apply stable bloom filter in practice. In addition, unlike double buffering bloom filter which uses two filters, a warm-up filter and an active filter, stable bloom Filter uses a single filter, so it costs a half amount of storage compared to double buffering bloom filter.

Temporal counting bloom filter[6] is similar to stable bloom filter. It sets cells as 'initial counter value' which is the same as max cell value of stable bloom filter. The difference is that temporal counting bloom filter decreases a cell value as much as 'decay factor', which is calculated by a provided algorithm, rather than constant 1. Temporal counting bloom filter also uses the same amount as stable bloom filter.

Double buffering bloom filter[7] uses two filters, a warm-up filter and an active filter. When inserting an item, if the item is in the active filter, it checks if it also exists in the warm-up filter, then set corresponding cells of warm-up filter only when the active filter is filled more than half of its capacity. If the item is not in the active filter, it inserts the item into the active filter, then also insert it to the warm-up filter only when the active filter is filled more than half. Decaying of the bloom filter, 'renewing' can be more appropriate in this case, is performed by exchanging the warm-up filters and the active filters when the active filters are full.

There are works in which bloom filters are used as embeddings which represent items or users of recommender systems[2][3][4]. Usually, the dimension of user or item vectors are enormous, dimensionality reduction is inevitable, and bloom filters can be a way of reducing dimensions. For example, a user embedding can be made by setting cells of a bloom filter of which indexes are generated by applying hashing with the value of an item. An item embedding can be generated in the same way.

Ⅲ. Probabilistic Bloom Filter

We suggest probabilistic bloom filter which resets a cell in proportion to the inverse of the count of the cell, which results in longer existence of important cells. We regard a cell as being 'important' when its count is high because it is used to check existence of many items.

Inserting is performed by adding 1 to all corresponding cells, and it updates the total sum of each count of cells and the number of non-zero cells of the filter. To make the filter decay, it first calculates the number of cells to reset to zero by subtracting a predefined configured number of non-zero cells from the current number of non-zero cells. Then it chooses non-zero cells to reset with probabilities in proportion to the inverse of the count of the cells. Inserting and decaying procedures are shown in Figure1 and Figure 2, respectively.

Fig 1.

Algorithm for inserting an item into the bloom filter

Fig 2.

Algorithm for Decaying of the bloom filter

Since it always maintains a specific number of zero cells, it never becomes full and users don't have to worry about how to find out the correct parameter for decay. This problem about deciding parameters related to decay is not trivial in online learning. For stable bloom filter and temporal counting bloom filter, algorithms are provided to decide the number of cells to decay or the decay factor, but the resulting values are not usually integers. So users can't help using rounded values which can result in not guaranteeing properties like false positive rate when they are used over a long period in online learning situations.

Ⅳ. Comparison between decay bloom filters

We wanted to see how each bloom filter performs as an embedding in a context of online learning of a recommender system. So we made a bloom filter represent a user by inserting items which the user interacted with into the bloom filter. As a result, bloom filters were created as many as the number of users.

Movielens[8] dataset was used for the experiment because it has been used many times as a benchmark dataset for online learning[9][10][11] and personalized recommendation[12]. u1.test ~ u4.test of ml-100k dataset were used to calculate 4-fold cross validation results on various parameters. Only 4 and 5 ratings were treated as positive feedbacks and corresponding items were inserted into a user's bloom filter. Records of the dataset were sorted by their timestamps and the insertions were made by time since we meant to simulate an online learning situation.

Evaluation as to how well a bloom filter performs as an embedding was done in two aspects. The first is about precision of a bloom filter. It describes how accurately a filter judge if an item is stored in the filter. We measured the mean of precision of users' bloom filters by checking if all items appeared in users' records. The second is about the degree of preservation of similarity between embeddings. Good user embeddings should preserve close users closely after the dimensionality reduction is done. We measured the degree of preservation of cosine similarity using rank correlation(Kendall's tau) between two similarity rank sets - one was generated by bloom filter embeddings and the other was generated by user vectors without dimensionality reduction of which dimension is the number of items. Cosine similarity ranks were generated between a user and all the other users, and this procedure was repeated on all users.

The experimental parameters for each bloom filter are shown in Table 1. The dimension of filters and the number of hashing are commonly applied to all bloom filters. For stable bloom filter, the number of cells to decay is decided by other parameters like cell max and false positive rate using the provided algorithm[5]. Likewise, the decay factor of temporal counting bloom filter is calculated with other parameters by the algorithm[6]. As to double buffering bloom filter, various thresholds are examined for double buffering bloom filter rather than only 'half' for inserting an item into a warm-up filter and 'full' for exchanging a warm-up filter and an active filter because a full bloom filter is not so much useful as an embedding and there is a possibility that other thresholds for inserting are better than the threshold of 'half' when domain differs. Probabilistic bloom filter has the smallest number of parameters among all, and actually non-zero cell ratio, which means how much the filter can be filled maximally (0.2 means that more than 20% cells cannot be set), is the only one needed.

Table 1.

Parameters of Bloom Filters in Experiments

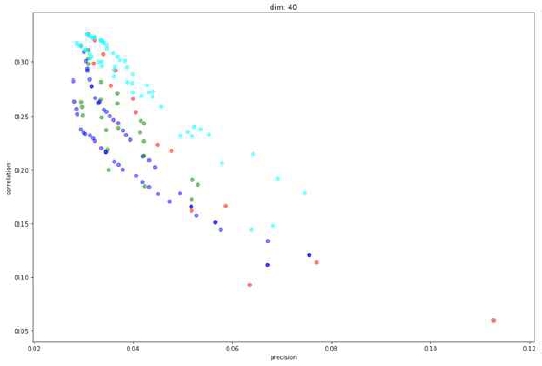
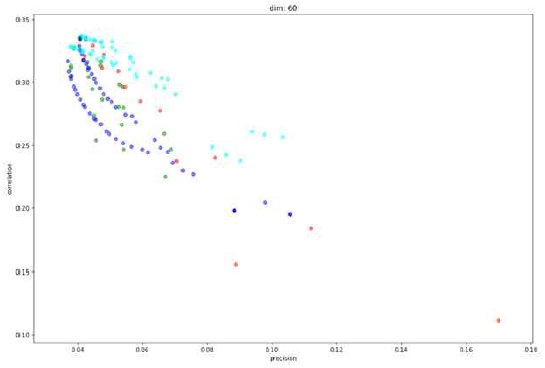
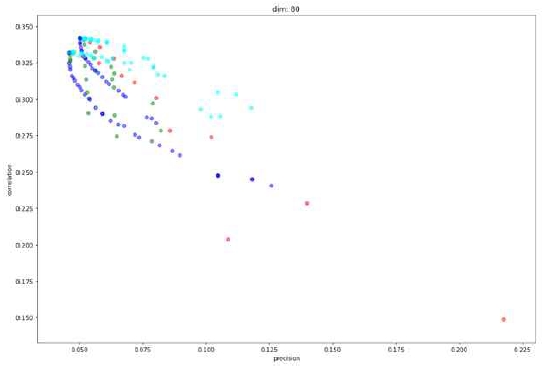
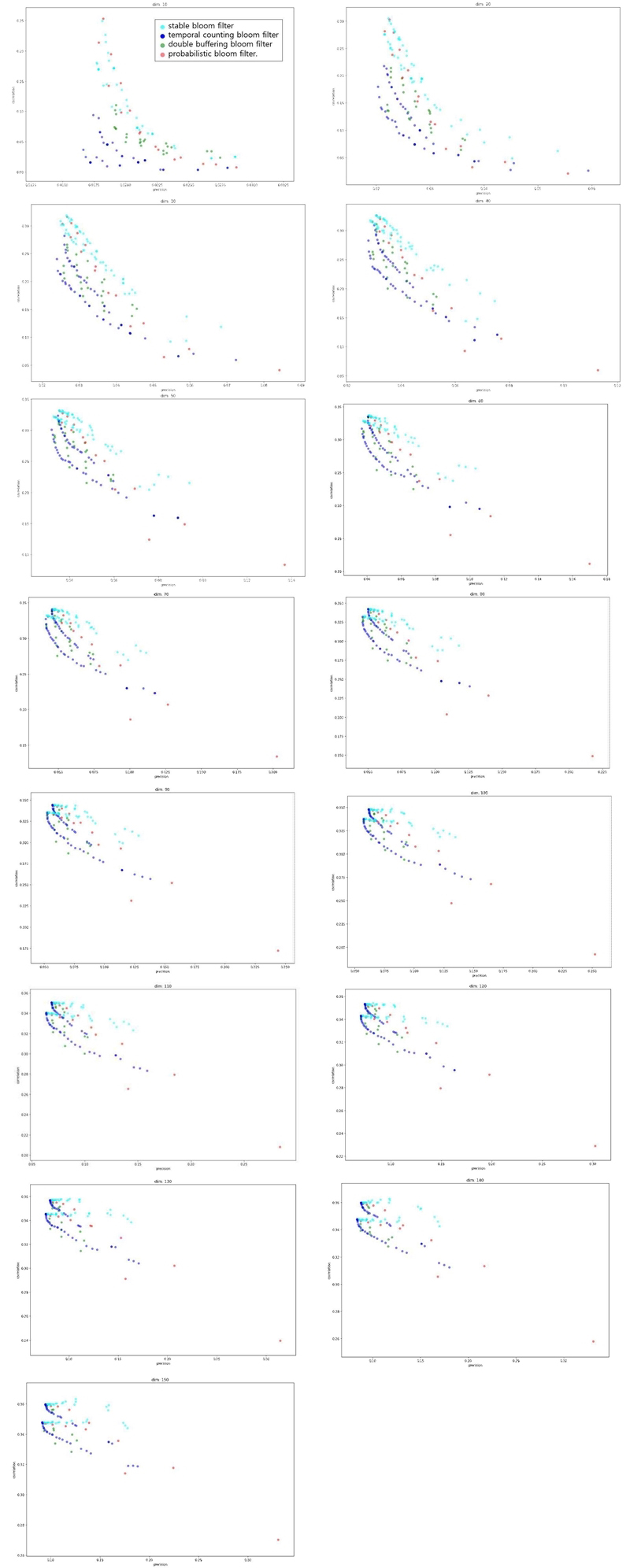
Some experimental results are shown in Figure 3~6. Cyan is stable bloom filter, blue is temporal counting bloom filter, green is double buffering bloom filter, and red is probabilistic bloom filter. Results of every dimension can be found in Appendix. Since there is a tradeoff between precision and rank correlation, there are no such 'best' parameters per bloom filters. So the results need to be interpreted by judging how far each graph of bloom filters appears from its origin as a whole. When the dimension of bloom filters was 20, stable bloom filter showed the best results, followed by probabilistic bloom filter and double buffering bloom filter, and temporal counting bloom filter came at last. When the dimension was increased to 40, 60, and 80, stable bloom filter was the best and the second was the probability bloom filter. Beside the results of overall performance, a unique trait of probabilistic bloom filter was found by this experiment. It shows far better precision than other filters when the dimension increases. For example, in Figure 5, the best precision achieved by probabilistic bloom filter is about 0.17 and no other filters reach near the value. This can be a useful property when precision is especially more important than rank correlation. We suppose that this result is due to the trait of probabilistic bloom filter that rarely resets important cells which are set by many items.

Fig 3.

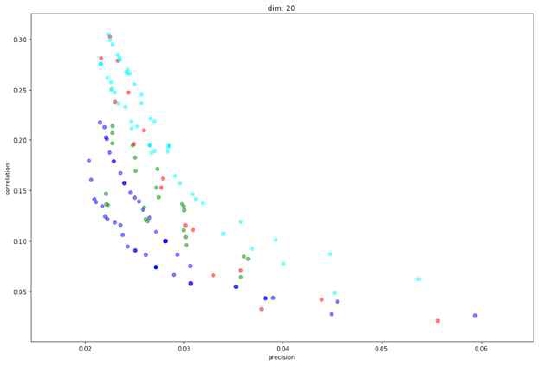
Comparison of correlation and precision with dimension of bloom filters = 20(Cyan- stable bloom filter, Blue- temporal counting bloom filter, Green- double buffering bloom filter, Red- probabilistic bloom filter)

Fig 4.

Comparison of correlation and precision with dimension of bloom filters = 40

Fig 5.

Comparison of correlation and precision with dimension of bloom filters = 60

Fig 6.

Comparison of correlation and precision with dimension of bloom filters = 80

Ⅴ. Conclusion

We compared various bloom filters which can decay as embeddings in online learning context of recommender systems. Besides existing bloom filters, we suggested 'probabilistic bloom filter' which can remember important cells longer. It never makes bloom filters full or emptier than necessary in an online learning situation while other bloom filters can suffer such problems because the calculated number of cells to decay or a decay factor must be rounded to become an integer. The overall performance over precision - rank correlation tradeoff was measured using Movielens dataset. Stable bloom filter showed the best results overall in this setting and probabilistic bloom filter was the second. When it comes to precision, probabilistic bloom filter showed that it can achieve higher precision than all the other bloom filters at the expense of rank correlation, so we expect it to be used in an online learning situation where precision is more important than rank correlation.

Acknowledgments

This research was supported by Korea National Open University Research Fund in 2017.

References

• McMahan, H. Brendan, Gary Holt, David Sculley, Michael Young, Dietmar Ebner, Julian Grady, Lan Nie, et al., "Ad click prediction: a view from the trenches", in Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, Chicago, USA, p1222-1230, Aug.), (2013.
• Pagare, Reena, and Anita Shinde, "Recommendation system using bloom filter in mapreduce", International Journal of Data Mining & Knowledge Management Process, 3(6), p127-134, Nov.), (2013. [https://doi.org/10.5121/ijdkp.2013.3608]
• Pozo, Manuel, Raja Chiky, Farid Meziane, and Elisabeth Métais, "An item/user representation for Recommender systems based on Bloom filters", in IEEE Tenth International Conference on Research Challenges in Information Science (RCIS 2016), Grenoble, France, p1-12, June), (2016. [https://doi.org/10.1109/rcis.2016.7549311]
• Serrà, Joan, and Alexandros Karatzoglou, "Getting deep recommenders fit: Bloom embeddings for sparse binary input/output networks", in Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, p279-287, Aug.), (2017.
• Deng, Fan, and Davood Rafiei, "Approximately detecting duplicates for streaming data using stable bloom filters", in Proceedings of the 2006 ACM SIGMOD international conference on Management of data, Chicago, USA, p25-36, June), (2006. [https://doi.org/10.1145/1142473.1142477]
• Zhao, Yaxiong, and Jie Wu, "The design and evaluation of an information sharing system for human networks", IEEE Transactions on Parallel and Distributed Systems, 25(3), p796-805, Mar.), (2014.
• Chang, Francis, Wu-chang Feng, and Kang Li, "Approximate caches for packet classification", in IEEE INFOCOM (Vol. 4), HongKong, China, p2196-2207, Mar.), (2004. [https://doi.org/10.1109/infcom.2004.1354643]
• GroupLens at the Univ. of Minnesota, MovieLens 100K Dataset, [Internet] Available: https://grouplens.org/datasets/movielens/100k/ (Accessed 03 June 2019).
• Blondel, Mathieu, Akinori Fujino, and Naonori Ueda, "Convex factorization machines", in Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Porto, Portugal, p19-35, Sep.), (2015. [https://doi.org/10.1007/978-3-319-23525-7_2]
• Yamada, Makoto, Wenzhao Lian, Amit Goyal, Jianhui Chen, Kishan Wimalawarne, Suleiman A. Khan, Samuel Kaski, Hiroshi Mamitsuka, and Yi Chang, "Convex factorization machine for toxicogenomics prediction", in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, Canada, p1215-1224, Aug.), (2017. [https://doi.org/10.1145/3097983.3098103]
• Lin, Xiao, Wenpeng Zhang, Min Zhang, Wenwu Zhu, Jian Pei, Peilin Zhao, and Junzhou Huang, "Online Compact Convexified Factorization Machine", in Proceedings of the 2018 World Wide Web Conference, Lyon, France, p1633-1642, Apr.), (2018. [https://doi.org/10.1145/3178876.3186075]
• Wang, Jun, Lantao Yu, Weinan Zhang, Yu Gong, Yinghui Xu, Benyou Wang, Peng Zhang, and Dell Zhang, "Irgan: A minimax game for unifying generative and discriminative information retrieval models", in Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval, Shinjuku, Japan, p515-524, Aug.), (2017.