Causal Relations and Temporal Interval Relations from Multiple Streams with Multiple Events

Ⅰ. Introduction

Data mining is a technology used to analyze a large amount of accumulated data and to extract valuable knowledge from the data for decision-making. It can be widely used in areas such as market analysis, decision support, fraud detection, customer classification, medical care, and so on [1], [2], [3], [4], [25]. Recently, many works have focused on the temporal data mining for discovering temporal knowledge from a temporal data set. The knowledge consists of sequential patterns [5], periodic patterns [6], frequent episodes [3], frequent temporal interval relations [7], similarity [8], and causality of events [9], [10], [11], [12], [13], [14], [15].

Temporal data sets can be classified into either a time point-based data set or an interval-based data set. When a time-point-based event data from stream data sources is gathered, its interval or duration to represent its continuity is generally not known. Thus, an interval-based data set is typically obtained from a time-point-based data set. An interval-based event holds summarized information of time-point-based events. From the temporal relations of interval-based events, called “temporal interval relations”, more important knowledge can be discovered such as the causality of events.

Also, a temporal data set can be classified into four categories according to the number of streams and the number of concurrent events as follows:

• 1. Single Stream and Single Event (SSSM) [3]; SSSM is a set of events from single stream, where one time slot contains only one event.
• 2. Single Stream and Multiple Events (SSME) [4], [6], [8]; SSME is a set of events from a single stream, where one time slot contains multiple events.
• 3. Multiple Streams and Single Events (MSSE); MSSE is a set of events from multiple streams, where one time slot contains only one event.
• 4. Multiple Streams and Multiple Events (MSME) [7], [9], [16]; MSME is a set of events from multiple streams, where one time slot contains multiple events.

The sequential pattern mining problem was introduced by Agrawal and Srikant [17]. Sequential pattern mining is used to find all frequent subsequences from a set of sequences. From frequent patterns, we can find the order of events. This order can be used in a business strategy. Examples of interval-based event data include library lending, stock fluctuation, patient diseases, meteorology data, etc. Wu and Chen [7] defined a new type of non-ambiguous temporal pattern for interval-based event data. They found that patterns discovered by the Allen-based approach have ambiguity problems. To solve the ambiguity problems, he proposed the TPrefixSpan algorithm.

In this paper, we propose a new temporal data mining method that discovers temporal interval relations between interval-based events which are computed from a time-point-based data set. Also, we will discuss the casual relations among interval-based events. The objective of our research is to develop an algorithm to process big-data from a selected hospital. Each department in the hospital treats many patients and produces medical records for the patients. Each medical record has several events (symptoms or the result of check-ups). Each patient is a stream source and one medical record contains many events. Therefore, we selected the MSME data set.

The basic concept of our method is summarized as follows, in which temporal interval relations and causal relations are discovered from a MSME data set:

• 1. Compute frequent event types from MSME data set
• 2. For each stream and each frequent event type, compute continuous event sequences from MSME data set
• 3. Summarize each continuous event sequence into one interval-based event
• 4. Discover temporal interval relations from interval-based events
• 5. Discover causal relations from temporal interval relations
• 6. Discover frequent causal relations from a set of causal relations
• 7. Compute the net effect of events on other events from component graphs for frequent causal relations.

Generally, patient medical records are stored in a hospital database in the timestamp order. From the hospital database, we aim to discover rules (or knowledge) to properly treat patients. Our method can be easily applied to the medical field for discovering useful and effective knowledge (frequent causal relations).

The remainder of the paper is organized as follows. In Chapter Ⅱ, we discuss the related works. In Chapter Ⅲ, the terminologies and definitions related to temporal relations and causal relations are described. In Chapter Ⅳ, our algorithm for mining temporal interval relations among interval-based events and their causal relations is described. In Chapter Ⅴ, the proposed method is analyzed through the experiments. In Chapter Ⅵ, the conclusion and future works are discussed.

Ⅱ. Related Works

Temporal data mining discovers useful knowledge from a temporal data set. Temporal data mining methods and their mining results can contain frequent event sequences [4], [16], frequent episodes [3], periodic patterns [6], frequent temporal interval relations [7], causality of events [9], [10], [11], [12], [13], [14], [15], or similarity [8]. Several variations of the Apriori algorithm have been proposed to improve basic sequential pattern mining algorithms such as GSP [17] and SPIRIT [18]. GSP is a technique used to discover generalized sequential patterns that incorporate user-specified time constraints. SPIRIT is a technique used for discovering all frequent sequences that satisfy a user-defined regular expression constraint. An episode has a collection of events with a partial order. Mannila, et al. [19] introduced the framework of frequent episodes discovery in event sequences. Laxman et al. [3] introduced generalized episodes. A generalized episode incorporates event duration information explicitly with the episode structure. Each event in the episode has a duration which is previously determined by the domain specialists. Frequent generalized episodes assist the diagnosis of root causes of persistent fault situations. Periodic patterns are recurring patterns that have temporal regularities in a time-series data set. Huang et al. [6] proposed a more general model of asynchronous periodic patterns from a sequence of event sets where a time slot can contain multiple events.

More recently, studies on mining useful patterns from temporal interval data have been initiated [20], [21], [22]. However, since the temporal relation rule discovery from interval data is very complicated, no noticeable progress has been made thus far. Also, summarizing a sequence of events into one interval-based event is unreasonable because some events in the sequence cannot be continuous or persistent. The sequence of events needs to be split into continuous subsequences and each subsequence needs to be summarized into one interval-based event. Periodic patterns exist in many types of data. For example, tides, planet trajectories, daily traffic patterns, and power consumptions present certain periodic patterns. Many emerging applications have been made, including stock market price movement, earthquake prediction, telecommunication network fault analysis, repeat detection in DNA sequences, and occurrence of recurrent illnesses. In [9], [14], [15], a method was proposed to detect adverse drug reactions. This is a domain-driven data mining method.

In [22], a method for finding the temporal interval relation rules from a temporal data set was proposed. The method can extract temporal interval relation rules from a temporal interval data set by using Allen's theory. However, the method does not measure the extent to which one event affects another event. If we can determine the degree of influence of each event, we can find a major source event for a specific event. If we have knowledge of the time-gap between interval-based events, we can also find very useful knowledge that can predict the occurrence time of future events. In [23], a method of mining positive and negative association rules was proposed. Positive association rules have a positive effect and negative association rules have a negative effect on association rules. However, there is a limit to analyzing the causality among events since the method computes an influence using association rules based only on the support of events and the confidence of association rules. Thus, it is necessary to develop a new measurement to represent the causality among events. Terminologies and definitions related to temporal interval relations and causal relations will be given in this section. Also, the way in which causal relations are discovered from temporal interval relations will be discussed.

Ⅲ. Temporal Interval Relation and Causal Relations

Terminologies and definitions related to temporal interval relations and causal relations will be given in this section. Also, the way in which causal relations are discovered from temporal interval relations will be discussed.

Ⅳ. Algorithm for Mining Temporal Interval Relations

In this section, we introduce an algorithm for mining temporal interval relations among interval-based events and their causal relations. It consists of the summarization of event sequences into interval-based events, as well as the discovery of temporal interval relations among interval-based events, and their causal relations. From causal relations, the degree of the cause-and-effect between interval-based events will be computed.

4-1 Algorithm

DB is a database of transactions. Each transaction consists of a customer Cid, a transaction-time t, and a set of events. A customer can issue one transaction at one time-point. That is, all of the timestamps of transactions issued from a customer differ. All events in a transaction have the same timestamp. Our algorithm can be summarized as shown in Table 1. In Step 3, a sequence of time-point-based events was split into subsequences if the sequence is not continuous. If a discontinuous sequence of the same type of events is summarized into one interval event, the interval event might not reasonably represent the actual interaction of events, as in Example 1. In Step 5, τ_interval-gap is needed to remove meaningless temporal interval relations. τ_interval-gap is greater than τ_gap.

Table 1.

Algorithm (DFCR-CRc) to discover frequent causal relations from causal relations

Example 1. Suppose that event sequences occur such as ES(Cid, A) =< (Cid, A, 1)(Cid, A, 3)(Cid, A, 4) (Cid, A, 10)(Cid, A, 12) >, ES(Cid, B) =< (Cid, B, 3)(Cid, B, 6) >, and ES(Cid, C) =< (Cid, C, 7)(Cid, C, 9) >.

Case 1: Tgap is not considered.

Three interval events <Cid, A, [1,12]>, <Cid, B, [3,6]>, and <Cid, C, [7,9]> are discovered. From these three interval events, the causal relations, A→B and A→C, are discovered.

Case 2: Tgap is considered and τ_gap is 3.

<Cid, A, [1,12]> is split into two interval relations, <Cid, A, [1,4]> and <Cid, A, [10,12]>. In this case, causal relations, A→B and C→A, are discovered.

Case 2 is more reasonable than Case 1 because an event A does not persist in an interval [5,9] (Tgap> τ_gap). Case 1 and Case 2 have different meanings because their causal relations differ.

All causal relations among events can be expressed by a directed graph, called CR-Graph. CR-Graph is defined in Definition 5. In CR-Graph, a node represents an interval-based event and an edge denotes a causal relation. Also, each edge x→y has a label Cust(x→y), which is a set of customers who support the causal relation.

Definition 5. (Causal Relation Graph: CR-Graph) CR-Graph is a directed graph. Each node represents an interval-based event. Each edge represents the causal relation between two interval-based events. The label on an edge denotes a set of customers who support the causal relation.

We can find frequent component graphs for causal relations from CR-Graph by examining the labels on the edges of CR-Graph. Assume that a component graph (A→C←B) in CR-Graph is frequent and its support count is 50. If Cust(A→C) and Cust(B→C) have 100 customers and 50 customers, respectively, and the support counts of interval-based events A and B are 200 and 50, respectively, we can infer that event B is the essential cause of C rather than event A because C always occurs when B occurs.

Discovering the cause-and-effect among events from causal relations considering only their supports has some shortcomings. Assume that the support of causal relation A→B and the support of event A are 0.3 and 0.3, respectively. If the confidence is used as the measure of causality, we can only infer that event A has an absolute effect on event B since the confidence of causal relation A→B is 1. If the support of B is 0.7, B can be due to other causes. Thus, we need a new evaluation measurement to show the rate of the effect of A on B. Let A→B be a causal relation in CR-Graph. We will define a new measurement NetEff(A→B) which computes the rate of the net effect of A on B. The measurement NetEff(A→B) is defined in Definition 6.

Definition 6. Net effect of X on B, NetEff(X→B), is defined as follows.

$\[ \begin{array}{c}NetEff\left(X\to B\right)=\frac{1}{2}\left(\frac{\text{sup}\left(X\to B\right)}{\text{sup}\left(X\right)}+\frac{\text{sup}\left(X\to B\right)}{\text{sup}\left(B\right)}\right)-max\left\{\frac{1}{2}\left(\frac{\text{sup}\left(Y\to B\right)}{\text{sup}\left(Y\right)}+\frac{\text{sup}\left(Y\to B\right)}{\text{sup}\left(B\right)}\right)\left|Y\to B\in FCR\wedge X\ne Y\right.\right.\hfill \\ \left.wher FCR is a set of frequent causal relation.\right\}\hfill \\ \begin{array}{c}Expression 1:Eff\left(X\to B\right)=\frac{1}{2}\left(\frac{sup\left(X\to B\right)}{sup\left(X\right)}+\frac{sup\left(X\to B\right)}{sup\left(B\right)}\right)\hfill \\ Expression 2:=max\left\{\frac{1}{2}\left(\frac{sup\left(Y\to B\right)}{sup\left(Y\right)}+\frac{sup\left(Y\to B\right)}{sup\left(B\right)}\right)\left|Y\to B\in FCR\wedge X\ne Y\right.\right\}\hfill \end{array}\hfill \end{array} \]$

Part $$ \frac{\text{sup}\left(X\to B\right)}{\text{sup}\left(X\right)}$$of Expression 1 denotes the rate that an event B can occur when an event X occurs. Part $$ {\frac{\text{sup}\left(X\to B\right)}{\text{sup}\left(X\right)}}^{.}$$ of Expression 1 denotes the portion of B affected by X. Eff(X→B) is represented by an average of two parts. Expression 2 is the maximum effect of other events on B. The net effect of X on B is represented by Eff(X→B) - max{Eff(Y→B)| Y→B∈FCR∧X≠Y}. By using NetEff, we can order the net effects of interval-based events in a component graph of CR-Graph. The ordered NetEffs of causal relations in a component graph can be used to discover the major source events for a target event.

Our algorithm (see Table 1) discovers a set of frequent causal relations from a set of temporal interval relations. We call our algorithm DFCR-CRc (Discovering Frequent Causal Relations from Causal Relations which can be from infrequent temporal interval relations). We can consider another algorithm to discover causal relations from only frequent temporal relations, called DFCR-FIRc (Discovering Causal Relations from Frequent Temporal Interval Relations). DFCR-CRc discovers more frequent causal relations than DFCR-FIRc because different temporal interval relations (which can be infrequent) can be transformed into the same causal relation.

Ⅴ. Experimental Results

From Experiments were carried out while varying time-constraint parameters such as τ_gap, τ_before, τ_overlap, τ_during, and MinSupport. The number of interval events, temporal interval relations, and causal relations will be computed by varying the parameters. The experiments are performed mainly for analyzing: (1) the DFCR-FIR method, for discovering frequent causal relations from frequent interval relations which have been computed without time-constraint (τ_gap)between the adjacent same type events, (2) the DFCR-FIRc method, for discovering frequent causal relations from frequent interval relations which have been computed with the time-constraint between the adjacent same type of events, and (3) the DFCR-CRc method, for discovering frequent causal relations from causal relations which have been computed from interval relations with the time-constraints between the adjacent same type of events.

The description of data set is shown as in Table 2. The data set has been artificially generated. Each transaction in the data set consists of three fields: transaction ID, transaction time, and a set of events.

Table 2.

Description of the Data Set

From the experiments, we analyze the change of the followings.

• (1) Number of interval events for customers (#IE)
• (2) Number of interval relations for customers (#IR)
• (3) Number of causal relations for customers (#CR)

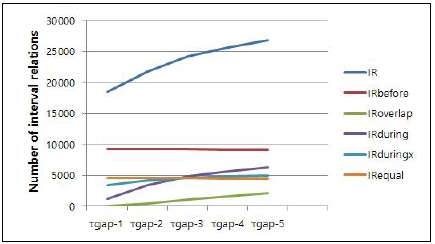
Also, through the experiments, we will show the changes of the number of interval relations for each interval relation (IR) type. Five types of interval relations exist (IR_before, IR_overlap, IR_during, IR_duringx, and IR_equal). To find causal relations, only three IR types (IR_before, IR_overlap, IR_during) will be considered. IR_duringx is a during(X,Y) where X.vs=Y.vs. Therefore, we cannot discern X and Y as a cause event. Also, from equal(X,Y), we cannot discern X and Y as a cause event.

Table 3.

Descriptions for some abbreviations

To discover frequent causal relations, we can choose one of three methods (DFCR-FIR, DFCR-FIRc or DFCR-CRc) as follows. The notation “→” denotes computation flows.

Method DFCR-FIR: IE →IR → FIR → FCR
Method DFCR-FIRc: IEc →IRc → FIRc → FCR-FIRc
Method DFCR-CRc: IEc → IRc → CRc → FCR-CRc

Constraint_Tgap (Tgap<τ_gap) must be satisfied to split a sequence of the same type of events into subsequences. If τ_gap is infinite, the sequence of events is transformed into one interval event. This might not be reasonable because an event might intermittently (rather than continuously) occur. The values of parameters such as τ_before,τ_overlap, and τ_during are needed to discover a reasonable causal relation between two temporal interval events. Their values are generally determined by domain specialists.

While varying τ_gap, we analyze the number of causal relations for two methods (DFCR-FIRc and DFCR-CRc). The DFCR-FIR method is the special case of DFCR-FIRc (the case τ_gap is infinite).

We show that the number of frequent causal relations discovered by DFCR-CRc is more than that by DFCR-FIR or DFCR-FIRc. In other words, the knowledge discovered by DFCR-CRc is much richer than that discovered by DFCR-FIR or DFCR-FIRc.

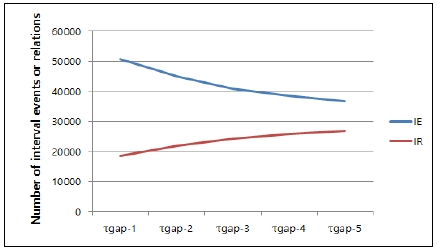
In Fig. 1, we can see that the number of interval events is decreased when τgap is increased. However, we found that the number of temporal interval relations is increased while τgap increases. As the length of the τgap increases, the duration of the interval events also increases. We found that there can be more temporal interval relations between long interval events and short interval events than those between only short interval events. If long interval events do not clearly represent the persistency of events, their temporal interval relations are also not reasonable.

Fig. 1.

Number of interval events or interval relations

As shown in Fig. 2, when τ_gap is increased, three types of interval relations, including IR_overlap, IR_during, and IR_duringx have an effect on the increase of the number of temporal interval relations. For example, long duration interval events can be more closely related to short duration events by “during”, “duringx”, or “overlap”. From Fig.1, we can see that the size of IR is larger than that of IRc, because IR is computed when τ_gap is infinite.

Fig. 2.

Number of interval relations for IR types

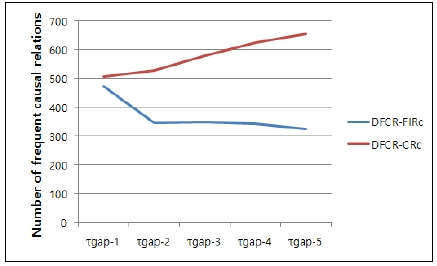
Fig. 3 shows that for all values of τ_gap, FCR-CRc contains significantly more information than FCR-FIR and FCR-FIRc. FCR is a set of causal relations when τ_gap is infinite (∞). As a result, DFCR-CRc discovers much more information from the time-point data set.

Fig. 3.

Number of causal relations for varying τgap

To determine the interval relation types that have an effect on the frequent causal relations, we inspect the change of the number of frequent causal relations while varying the time-constraints of τ_before, τ_overlap, and τ_during. Only these three constraints have an effect on causal relations.

Also, we compare only two methods, DFCR-CRc and DFCR-FIRc, because DFCR-FIR is a special case of DFCR-FIRc when τ_gap is infinite. In Fig. 4, for the given parameter values of τ_gap(=3), τ_during (=1), τ_overlap (=1), and MinSupport(=0.1), we find the degree to which a parameter τ_before has an effect on the number of causal relations. In Fig. 5, for given parameter values of τ_gap(=3), τ_during (=1), τ_before (=1), and MinSupport(=0.1), we find the degree to which a parameter τ_overlap has an effect on the number of causal relations. In Fig. 6, for given parameter values of τ_gap (=3), τ_overlap (=1), τ_before (=1), and MinSupport(=0.1), we find how a parameter τ_during has an effect on the quality of causal relations. As shown in Fig. 4, Fig. 5, and Fig. 6, for all parameter values, DFCR-CRc discovers considerably more causal relations than DFCR-FIRc. This is because different infrequent interval relations can be transformed into the same causal relation. For example, overlap(A,B) and before(A,B) produce the same causal relation of A→B. Let #rel(X,Y) be the number of a relations rel(X,B). Even though both temporal interval relations are infrequent, if (#overlap(A,B) + #before(A,B) ) > MinSupportCount, the causal relation A→B is frequent.

Fig. 4.

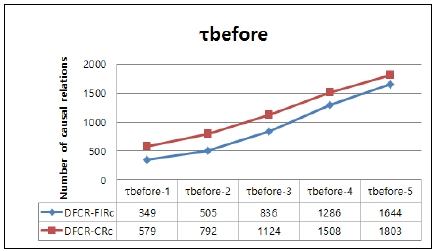
Number of causal relations discovered while varying a parameter τbefore (for the following fixed parameters of τgap=3, τinterval-gap=3, τduring=1, τoverlap=1, MinSupport=0.1)

Fig. 5.

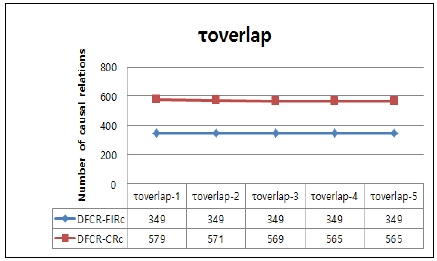
Number of causal relations found while varying a parameter τoverlap (for the following fixed parameters such as τgap=3, τinterval-gap=3, τduring=1,τbefore=1, MinSupport=0.1)

Fig. 6.

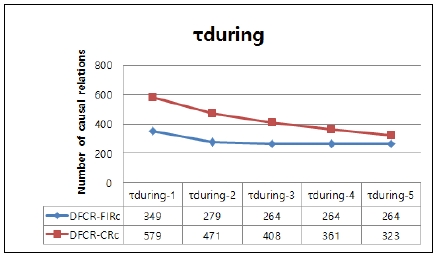
Number of causal relations discovered while varying a parameter τduring (for the following fixed parameters such as τgap=3, τinterval-gap=3, τduring=1,τbefore=1, MinSupport=0.1)

As shown in Fig. 4, when τ_before increases, the number of causal relations increases in DFCR-CRc and DFCR-FIRc because Constraint_before becomes stronger when the value of τ_before decreases. For example, for two interval-based events, (A,[8,10]) and (B,[12,14]), if τ_before =1, there is no temporal interval relation, but if τ_before=2, there is a temporal interval relation before(A,B) and a causal relation A→B. As shown in Fig. 5, for τ_overlap, when its value is increasing, the number of causal relations is almost the same, but the number of causal relations for a high value is always less than that of its low value. This is because Constraint_overlap becomes stronger when the value of τoverlap increases. For example, for two interval-based events (A, [10,14]) and (B, [12,15]), if τ_overlap=1 or τ_overlap=2, there is a temporal interval relation overlap(A, B) and a causal relation A→B, but if τoverlap=3, there is no temporal interval relation because the condition of (startTime(B) - startTime(A))> 2 must be satisfied. Fig. 6 shows that for τ_during, when its value increases, the number of causal relations decreases. This is also because Constraint_during becomes stronger when the value of τduring becomes larger. For example, for two interval-based events (A, [10,16]), and (B, [12,15]), if τ_during=1 or τ_during=2, a temporal interval relation during(B, A) and a causal relation A→B occur, but if τ_during=3, no temporal interval relation exists because the condition of (startTime(B) - startTime(A))> 2 is not satisfied.

From the result of experiments (see Fig. 4, 5, and 6), we can find that the DFCR-CRc method discovers much more causal relations than DFCR-FIRc. This is because of the two following facts.

Fact 1: The number of different causal relations is less than or equal to the number of different interval relations.

Fact 2: The number of frequent causal relations discovered by DFCR-CRc is greater than or equal to the number of causal relations discovered by DFCR-FIRc.

Assume that #P denotes the number of relations P. For example, #before(A, B) denotes the number of temporal interval relations before(A, B). Fact 1 exists because several different temporal interval relations can be mapped into one causal relation. For example, two temporal interval relations before(A, B) and overlap(A, B) are both represented by one causal relation A→B. In DFIR-CRc, even though before(A, B) and overlap(A, B) are both infrequent interval relations, #(A→B) can be frequent because (#(A→B)_before + #(A→B)_overlap) can be greater than or equal to the given MinSupportCount. Therefore, Fact 2 is always true.

It is better to discover frequent causal relations from temporal interval relations that could be infrequent than to discover frequent causal relations from frequent temporal interval relations. That is, DFCR-CRc can find frequent causal relations from temporal interval relations which might be infrequent. Therefore, the frequent causal relations discovered by DFIR-CRc can represent more important knowledge than those discovered by DFIR-FIRc. Parameters τ_before,τ_overlap, andτ_during are properly adjusted by domain experts. For example, a patient can have symptom B after symptom A disappears, and another patient might have symptom B during the lifetime of symptom A. In this case, it is reasonable to infer that A is a cause symptom for B. Our proposed DFCR-CRc method discovers more valuable knowledge than DFCR-FIR or DFCR-FIRc.

Ⅵ. Conclusion and Future Works

We proposed a method that discovers temporal interval relations and causal relations from time-point-based events. To discover qualitative information from the event set, we found that a sequence of persistent events of the same type needs to be summarized into one interval event. It may be difficult to discover the temporal relations directly from the time-point-based events. Thus, we summarized the sequences of time-point-based events of the same type into interval-based events. From the interval-based events, temporal interval relations and causal relations were discovered. From the temporal interval relations, we can find effective causal relations if some parameters such as τ_before,τ_overlap,τ_during and MinSupport are properly selected by domain experts. We showed three methods (DFCR-FIR, DFCR-FIRc, and DFCR-CRc) used for discovering causal relations from temporal interval relations. Through the experiments, we found that the DFCR-CRc method discovers more effective and qualitative information than DFCR-FIRc and DFCR-FIR. We also proposed a new evaluation measurement that can be used for ordering the major causes of an event.

In future work, based on the history data of patients, we intend to develop a method to predict time-points or time intervals at which an event is likely to occur. It is also important to discover temporal and causal relations among events (symptoms).

References

• S. Laxman, P.S. Sastry, and K.P. Unnikrishnan, “Discovering frequent episodes and learning hidden markov models: A formal connection” IEEE Trans, Knowledge and Data Engineering, 17(11), p1505-1517, (2005).
• S. Laxman, and P.S. Sastry, “A survey of temporal data mining”, Sadhana, 31(2), p173-198, (2006). [https://doi.org/10.1007/bf02719780]
• S. Laxman, P.S. Sastry, and K.P. Unnikrishnan, “Discovering frequent generalized episodes when events persist for different durations” IEEE Trans, Knowledge and Data Engineering, 19(9), p1188-1201, (2007).
• H.Y. Yun, D.S. Ha, B.H. Hwang, and K.H. Ryu, “Mining association rules on significant rare data using relative support”, Journal of Systems and Software, 67(3), p181-191, (2003). [https://doi.org/10.1016/s0164-1212(02)00128-0]
• C.H. Lee, M.S. Chen, and C.R. Lin, “Progressive partition miner: an efficient algorithm for mining general temporal association rules” IEEE Trans, Knowledge and Data Engineering, 15(4), p1004-1017, (2003).
• K.Y. Huang, and C.H. Chang, “SMCA: a general model for mining asynchronous periodic patterns in temporal databases”, IEEE Trans, Knowledge and Data Engineering, 17(6), p774-785, (2005).
• S.Y. Wu, and Y.L. Chen, “Mining nonambiguous temporal patterns for interval-based events” IEEE Trans, Knowledge and Data Engineering, 19(6), p742-758, (2007).
• J.S. Yoo, and S. Shekhar, “Similarity-profiled temporal association mining” IEEE Trans, Knowledge and Data Engineering, 21(8), p1147-1161, (2009).
• H. Jin, J. Chen, H. He, C. Kelman, D. McAullay, and C.M. O'Keefe, “Signaling potential adverse drug reactions from administrative health databases” IEEE Trans, Knowledge and Data Engineering, 22(6), p839-853, (2010).
• Y. Mohammad, and T. Nishida, “Mining causal relationships in multidimensional time series” Smart information and knowledge management, Springer, Berlin Heidelberg, p309-338, (2010).
• J. Li, T.D. Le, L. Liu, J. Liu, Z. Jin, and B. Sun, B, “Mining causal association rules”, Proc. 2013 IEEE 13th International Conf. Data Mining Workshops (ICDMW), p114-123, Dec.), (2013. [https://doi.org/10.1109/icdmw.2013.88]
• S. Bleisch, M. Duckham, A. Galton, P. Laube, and J. Lyon, J, “Mining candidate causal relationships in movement patterns”, International Journal of Geographical Information Science, 28(2), p363-382, (2014). [https://doi.org/10.1080/13658816.2013.841167]
• H.D. Kim, M. Castellanos, M. Hsu, C. Zhai, T. Rietz, and D. Diermeier, “Mining causal topics in text data: iterative topic modeling with time series feedback”, Proc. 22nd ACM international conf. information & knowledge management, p885-890, Oct.), (2013.
• Y. Ji, H. Ying, J. Tran, P. Dews, A. Mansour, and R.M. Massanari, “A method for mining infrequent causal associations and its application in finding adverse drug reaction signal pairs” IEEE Trans, Knowledge and Data Engineering, 25(4), p721-733, (2013).
• I. Gurumurthy, and R. Jayamma, “A Technique for Mining Uncommon Causal Relations and Its Submission in Finding Adverse Drug Reaction Indication Pairs”, International Journal of Computer Science and Mobile Applications, 2(11), p55-61, (2014).
• J. Pei, J. Han, B. Mortazavi-Asl, J. Wang, H. Pinto, Q. Chen, U. Dayal, and M.C. Hsu, “Mining sequential patterns by pattern-growth: The prefixspan approach” IEEE Trans, Knowledge and Data Engineering, 16(11), p1424-1440, (2004).
• R. Srikant, and R. Agrawal, Mining sequential patterns: Generalizations and performance improvements, Springer, Berlin Heidelberg, p1-17, (1996). [https://doi.org/10.1007/bfb0014140]
• M.N. Garofalakis, R. Rastogi, and K. Shim, “SPIRIT: Sequential pattern mining with regular expression constraints”, Proc. VLDB, 99, p7-10, Sep.), (1999.
• H. Mannila, H. Toivonen, and A.I. Verkamo, “Discovery of frequent episodes in event sequences”, Data Mining and Knowledge Discovery, 1(3), p259-289, (1997).
• Y.L. Chen, and S.Y. Wu, “Mining temporal patterns from sequence database of interval-based events” Fuzzy Systems and Knowledge Discovery, Springer, Berlin Heidelberg, p586-595, (2006).
• Y.P. Huang, L.J. Kao, and F.E. Sandnes, “A prefix tree-based model for mining association rules from quantitative temporal data” Proc. 2005 IEEE International Conf. on Systems, Man and Cybernetics, 1, p158-163, Oct.), (2005.
• Y.J. Lee, J.W. Lee, D.J. Chai, B.H. Hwang, and K.H. Ryu, “Mining temporal interval relational rules from temporal data”, Journal of Systems and Software, 82(1), p155-167, (2009). [https://doi.org/10.1016/j.jss.2008.07.037]
• X. Wu, C. Zhang, and S. Zhang, “Efficient mining of both positive and negative association rules” ACM Trans, Information Systems, 22(3), p381-405, (2004).
• J.F. Allen, Maintaining knowledge about temporal intervals, Communications of the ACM, 26(11), p832-843, (1983). [https://doi.org/10.1145/182.358434]
• Giang-Truong Nguyen, Van-Quyet Nguyen, Sinh-Ngoc Nguyen, Kyungback Kim, Efficient Association Rule Mining based SON Algorithm for a Bigdata Platform, Journal of Digital Contents Society, 18(8), p1593-1601, Dec.), (2017.