사물 인터넷 환경에서 무선 센서 기기의 전력 효율적 데이터 전송주기 결정을 위한 최적화 모형

Ⅰ. 서론

무선 센서 네트워크는 환경 및 기후 데이터와 같은 광범위 지역의 대용량 데이터 수집 등 다양한 응용분야에 사용되고 있으며, 최근에 들어서는 사물인터넷(Internet of Things) 환경에 적용되면서 개인 심박 측정 센서 등과 같은 웨어러블 분야까지 확대되어 우리 생활과 더욱 밀접해지고 있다[1]. Fig.1은 사물인터넷 환경에서 웨어러블 센서 네트워크의 개략도를 보여준다[2]. 무선 센서 네트워크는 일반적으로 무선 센서 기기에서 특정 데이터를 수집하여 무선 인터넷 또는 무선 전용망을 통해 서버로 데이터를 주기적으로 전송하도록 작동한다. 이렇게 전송된 데이터들은 서버에서 축적된 후 딥러닝이나 빅데이터 분석 기법 등을 통하여 다양한 용도로 활용 가능하다.

Fig. 1.

Wearable Wireless Sensor Networks on Internet of Things[2]

그러나 무선 센서들은 전력자원의 한계를 가지므로, 무선 통신과 같은 전력소모가 큰 작업들을 원만히 수행하기 위해서는 운영에 있어 에너지 효율적 접근방식이 필요하다. 이를 위해 다양한 기법들이 제안되고 있는데, 특히 무선 센서에서 데이터를 수집하자마자 바로 무선 통신을 통해서 센서 서버나 센서 싱크(sink)로 보내는 것은 에너지 비효율적이므로, 수집된 센서 데이터를 모아서 보내는 방식(aggregation)이 일반적이다[3].

데이터 전송주기란 센서 데이터를 모아서 서버 또는 센서 싱크로 보낼 때 aggregate된 센서 데이터를 서버로 전송하는 주기를 뜻하는데, 전력 소비를 최소화하는 최적 데이터 전송주기를 구하는 것은 센서 기기의 효율적 운용을 위해 필수적이다. 왜냐하면 너무 짧은 센서 데이터 전송주기는 기기의 잦은 무선통신으로 인해 추가적인 전력소비를 초래할 수 있고, 반면 너무 긴 데이터 전송주기는 중간에 결함(오작동이나 고장)이 발생하는 경우 미전송된 센서 데이터의 유실량을 더욱 크게 만들 수 있기 때문이다.

그동안 효율적인 데이터 전송주기에 대한 연구들이 많이 이루어져왔으나 대부분은 수집 데이터의 aggregation 기법에 대한 실험적 접근방식(empirical approach)이 주를 이룬다[3],[4]. 따라서 본 연구에서는 기존 연구들의 접근방식과 다르게 확률 모형 기반의 에너지 소비 모델을 개발하고, 개발된 모델을 기반으로 전력소비를 최소화 하는 센서 데이터 전송주기를 구한다. 구체적으로 본 연구에서는 확률과정(stochastic process) 중 하나인 마코프체인(Markov chain)과 재생 보상 이론(renewal reward theory)을 사용 한다[5]. 또한, 실제 무선통신 장치의 파라미터들을 활용하여 제안한 모델과 최적 전송주기의 성능을 수치예제로 보였다. 본 연구의 결과는 실제 센서 네트워크 시스템의 개발, 적용에 정량적인 예측을 통한 가이드라인을 제공할 수 있을 것이다.

본 논문의 구성은 다음과 같다. 2장에서는 본 논문에서 사용하는 시스템 모델을 설명한다. 3장에서는 본 논문에서 제안하는 전력 효율적 데이터 전송주기 결정을 위한 최적화 모형과 그 해를 제시하고 4장에서는 수치 예제를 통해 본 논문에서 제안한 시스템 모델의 성능척도들을 살펴본다. 마지막으로 5장에서는 본 연구의 결론을 맺는다.

Ⅱ. 시스템 모델

본 논문은 기존 연구[6],[7]에서 정의한 시스템 모델들을 참고하여 적용하였으며, 시스템 모델에서 가정한 내용은 다음과 같다.

• 본 논문에서 가정하는 시스템은 무선 센서 기기와 하나의 센서 서버로 구성되어 있다.
• 센서 기기는 배터리로 운영되며, 무선 통신을 통해 서버와 연결된다.
• 센서 기기는 지속적으로 데이터를 수집하며, 수집한 데이터는 주기적으로 서버로 전송한다. 전송주기는 I로 나타내었다.
• 수집(aggregate)된 데이터를 서버로 전송할 때에는 무선 통신이 사용되며, 데이터 전송을 완료하는데 필요한 시간을 U로 표현한다.
• 센서 기기의 결함은 즉시 복구가 가능한 일시적 결함 (transient fault)으로 가정한다.
• 결함이 발생했을 때, 복구는 재부팅(reboot) 또는 수리(repair)로 이루어지며, 복구에 필요한 시간은 R로 표현한다.
• 센서 기기는 휘발성 메모리만 장착하였고 stable 저장장치를 장착하지 않았으므로, 결함 발생 시 이전까지 수집(aggregate)된 센서 데이터들은 유실된다.

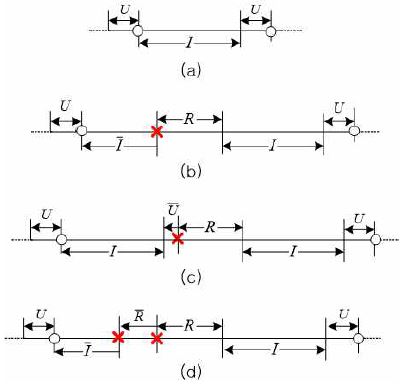
Fig.2는 앞에서 설명한 시스템 모델의 작동 예를 나타낸다.

Fig. 2.

Operation of the System Model

x 표시는 결함의 발생을, ○ 표시는 센서 기기의 데이터 전송이 성공적으로 완료된 시점을 나타내며, 윗줄 표시는 결함 발생으로 인하여 해당 작업이 완료되지 않았음을 의미한다. Fig. 2에 대한 자세한 설명은 3장에서 수식증명과 함께 다룬다.

본 연구는 센서 기기의 성공적인 데이터 전송완료 시점 간의 전력소모를 최소로 만드는 센서 서버로의 데이터 전송주기 I의 길이를 결정하는 것이다.

Ⅲ. 전력 효율적 데이터 전송주기 결정을 위한 최적화 모형

본 장에서는 센서 기기의 작동과 전력 소비에 대한 수리적 모형(mathematical model)을 구축하고, 이를 통해 최적의 데이터 전송주기 I^*를 구한다. 서론에서 언급하였듯이, 데이터 전송주기의 길이와 전력 소비 사이에는 상충관계(trade-off)가 존재하는데 본 장에서는 이러한 문제를 해결하기 위하여 확률과정(stochastic process) 중 하나인 마코프체인(Markov chain)을 사용하여 시스템을 전반적으로 분석한 후, 재생 보상 이론(renewal reward theory)을 사용하여 최적화 모형을 만들고 수치 해를 구한다. 마코프체인과 재생 보상 이론에 관한 보다 자세한 내용은 [5],[8]에서 찾아 볼 수 있다.

3-1 시스템 분석

센서의 데이터 전송완료시점들은 재생과정을 이루고, 센서 기기에 발생하는 결함은 파라미터 λ의 포아송과정(Poisson process)을 따른다고 가정하였으므로 n번째 결함발생시점 X_n들로 이루어진 확률과정 {X_n, n=0,1,2, …}은 이산시간 마코프체인(DTMC, discrete-time Markov chain)으로 모델링이 가능하다.

Fig. 3.

State Transition Diagram of the Discrete-time Markov Chain

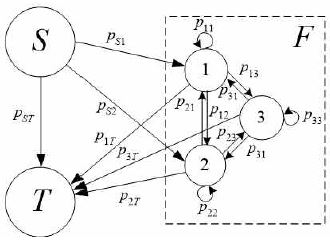
Fig. 3은 본 연구에서 다루는 마코프체인의 전이 다이어그램이다. 상태 ‘S’와 ‘T’는 임의의 사이클의 시작(start)과 종료(termination)를 나타내며, 여기서 사이클(cycle)이란 데이터 전송이 성공적으로 완료된 시점(Fig. 2의 ○ 참조)으로부터 다음 데이터 전송이 완료되는 시점 동안의 길이로 정의한다.

임의의 한 사이클 동안 발생한 센서 결함(failure)은 ‘F’영역과 같이 크게 3가지 상태로 구분된다. 상태 1은 센서 결함이 데이터 수집(aggregation) 중에 발생한 것을 나타내며, 상태 2는 데이터 전송(서버로의 upload) 중에 발생한 센서 결함을, 상태 3은 결함이 발생하여 복구(reboot 또는 repair)하는 중에 다시 센서 결함이 발생한 것을 나타낸다.

직전 상태가 i라는 가정 하에 다음 상태가 j일 조건부 확률을 P_ij (i,j∈{S,T,1,2,3})라고 정의하자. 이 조건부확률들로 이루어진 1-단계 전이확률행렬(transition probability matrix) P는 다음과 같다.

$\[ P=\left(\begin{array}{ccccc}0& p_{S1}& p_{S2}& 0& p_{\mathit{ST}}\\ 0& p_{11}& p_{12}& p_{13}& p_{1T}\\ 0& p_{21}& p_{22}& p_{23}& p_{2T}\\ 0& p_{31}& p_{32}& p_{33}& p_{3T}\\ 0& 0& 0& 0& 1\end{array}\right) \]$

(1)

여기서,

$$ p_{S1}=1-e^{-\lambda I},p_{S2}=e^{-\lambda I}-e^{-\lambda (I+U)},p_{\mathit{ST}}=e^{-\lambda (I+U)},$$

$$ p_{i1}=e^{-\lambda R}-e^{-\lambda (R+I)},$$

$$ p_{i2}=e^{-\lambda (R+I)}-e^{-\lambda (R+I+U)}$$,

$$ p_{i3}=1-e^{-\lambda R}$$,

$$ p_{\mathit{iT}}=e^{-\lambda (R+I+U)},(i=1,2,3)$$.

식 (1)의 각 원소에 해당하는 확률들은 다음과 같이 구할 수 있다. 상태 S에서 상태 1로의 전이확률 p_S1은 Fig. 2의 (b)에 해당하는 경우로서 데이터 전송이 성공적으로 끝난 후 임의의 사이클을 시작하여 데이터 수집 중에 센서 결함이 발생할 확률을 뜻한다. 이는 도착률 λ의 지수분포(exponential distribution)를 따르는 확률변수 X가 전송주기 I보다 작을 확률과 같으며 식 (2)와 같다.

$\[ p_{S1}=\text{Pr}(X\le I)={\int }_0^I\lambda e^{-\lambda x}\mathit{dx}=1-e^{-\lambda I} \]$

(2)

상태 S에서 상태 2로의 전이확률 p_S2는 Fig. 2의 (c)에 해당하는 경우로 센서 결함이 전송주기 I 동안에는 발생하지 않았다가 데이터 전송 중에 발생할 확률로서 이는 식 (3)과 같다.

$\[ p_{S2}=\text{Pr}(X\le I+U)-\text{Pr}(X\le I)=e^{-\lambda I}-e^{-\lambda (I+U)} \]$

(3)

상태 S에서 상태 T로의 전이확률 p_ST는 Fig. 2의 (a)에 해당하는 경우로서 전송주기와 데이터 전송 동안 어떠한 결함도 발생하지 않을 확률이므로 식 (4)와 같다.

$\[ p_{\mathit{ST}}=\text{Pr}(X\ge I+U)=e^{-\lambda (I+U)} \]$

(4)

상태 i(i=1,2,3)에서 상태 1로의 전이확률 p_i1은 이미 결함이 발생하여 기존의 데이터들이 손실되고, 복구 후에 전송주기 I가 진행되는 동안 결함이 발생할 확률로 식 (5)와 같이 구한다.

$\[ p_{i1}=\text{Pr}(X\le R+I)-\text{Pr}(X\le R)=e^{-\lambda R}-e^{-\lambda (R+I)} \]$

(5)

상태 i(i=1,2,3)에서 상태 2로의 전이확률 p_i2는 결함 발생으로 센서 기기가 복구된 후에 I 동안에는 결함이 발생하지 않았으나 데이터 전송(U) 중에 결함이 발생할 확률로 식 (6)과 같다.

$\[ p_{i2}=\text{Pr}(X\le R+I+U)-\text{Pr}(X\le R+I)=e^{-\lambda (R+I)}-e^{-\lambda (R+I+U)} \]$

(6)

상태 i(i=1,2,3)에서 상태 3으로의 전이확률 p_i3은 결함 발생으로 센서 기기가 복구되는 동안에 또 다시 결함이 발생할 확률로서 Fig. 2의 (d)에 해당한다.

$\[ p_{i3}=\text{Pr}(X\le R)=1-e^{-\lambda R} \]$

(7)

마지막으로, 상태 i(i=1,2,3)에서 상태 T로의 전이확률 p_iT는 결함이 발생하여 센서 기기가 복구된 후 전송주기, 데이터 전송이 연달아 진행되는 동안 결함이 발생하지 않을 확률로서 식 (8)과 같다.

$\[ p_{\mathit{iT}}=\text{Pr}(X\ge R+I+U)=e^{-\lambda (R+I+U)} \]$

(8)

이산시간 마코프체인의 전이확률행렬에서 행의 총합은 1이며, 앞에서 유도한 확률들은 이 조건을 만족함을 확인할 수 있다.

본 연구의 주목적은 전력소비를 최소화하는 데이터 전송주기를 구하는 것이므로 마코프체인의 상태전이확률뿐만 아니라 각각의 전이에 소비되는 에너지의 양들을 따로 계산해야 한다.

마코프체인이 상태 i에서 상태 j로 전이할 때 소비되는 조건부 에너지의 기댓값(expectation)을 E_i,j라고 정의하자. 센서가 어떤 확률변수의 길이 L 동안 사용하는 단위시간당 에너지 소비량을 γ_L이라고 하면 E_i,j는 다음과 같이 유도할 수 있다. 상태 S에서 상태 1로의 전이에 사용되는 에너지 소비량은 다음과 같다.

$\[ E_{S1}={\gamma }_I{\int }_0^I(x\cdot \frac{\lambda e^{-\lambda x}}{p_{S1}})\mathit{dx}={\gamma }_I(\frac{1}{\lambda }-\frac{I{e}^{-\lambda I}}{1-e^{-\lambda I}}) \]$

(9)

식 (9)에서 적분 값은 임의의 사이클이 시작된 후 결함이 발생할 때까지의 시간이 I보다 작은 경우의 조건부평균을 의미한다. 상태 S에서 상태 2로의 전이에 사용되는 에너지 소비량은 식 (10)과 같이 구한다.

$\[ E_{S2}={\int }_I^{I+U}(({\gamma }_{I}I+{\gamma }_U(x-I))\cdot \frac{\lambda e^{-\lambda x}}{p_{S2}})\mathit{dx}={\gamma }_{I}I+{\gamma }_U(\frac{1}{\lambda }-\frac{U{e}^{-\lambda U}}{1-e^{-\lambda U}}) \]$

(10)

상태 S에서 상태 T로의 전이에 사용되는 에너지 소비량은 식 (11)과 같이 간단히 구할 수 있다. Fig. 2의 (a)를 살펴보면 이는 자명하다.

$\[ E_{\mathit{ST}}={\gamma }_{I}I+{\gamma }_{U}U \]$

(11)

같은 논리로 상태 i(i=1,2,3)에서 상태 T로의 전이에 사용되는 에너지 소비량을 구하면 식 (12)와 같다.

$\[ E_{\mathit{iT}}={\gamma }_{R}R+{\gamma }_{I}I+{\gamma }_{U}U \]$

(12)

또한, 상태 i(i=1,2,3)에서 상태 1,2,3으로의 전이에 사용되는 각각의 에너지 소비량을 구하면 식 (13)-(15)를 얻는다.

$\[ E_{i1}={\int }_R^{R+I}(({\gamma }_{R}R+{\gamma }_U(x-R))\cdot \frac{\lambda e^{-\lambda x}}{p_{i1}})\mathit{dx}={\gamma }_{R}R+{\gamma }_I(\frac{1}{\lambda }-\frac{I{e}^{-\lambda I}}{1-e^{-\lambda I}}) \]$

(13)

$\[ E_{i2}={\int }_{R+I}^{R+I+U}(({\gamma }_{R}R+{\gamma }_{I}I+{\gamma }_U(x-R-I))\cdot \frac{\lambda e^{-\lambda x}}{p_{i2}})\mathit{dx}={\gamma }_{R}R+{\gamma }_{I}I+{\gamma }_U(\frac{1}{\lambda }-\frac{U{e}^{-\lambda U}}{1-e^{-\lambda U}}) \]$

(14)

$\[ E_{i3}={\int }_0^R({\gamma }_{R}x\cdot \frac{\lambda e^{-\lambda x}}{p_{i3}})\mathit{dx}={\gamma }_R(\frac{1}{\lambda }-\frac{R{e}^{-\lambda R}}{1-e^{-\lambda R}}) \]$

(15)

이제 Γ_iT를 상태 i에서 상태 T에 흡수될 때까지 평균 에너지 소비량이라 정의하면, 임의의 사이클 동안에 소비되는 평균에너지는 상태 S에서 시작하여 흡수상태 T에 들어가기까지 소비되는 평균 에너지 Γ_ST로 다음과 같이 표현이 가능하다.

$\[ {\Gamma }_{\mathit{ST}}=p_{\mathit{ST}}\cdot E_{\mathit{ST}}+p_{S1}(E_{S1}+{\Gamma }_{1T})+p_{S2}(E_{S2}+{\Gamma }_{2T}) \]$

(16)

식 (16)은 총합평균(total expectation)의 개념을 사용한 것으로서 재귀적으로 구할 수 있는데, 이와 같은 논리로 Γ_1T와 Γ_2T, Γ_3T를 구하여 정리하면 각각 식 (17)-(19)와 같다. 식 (16)에는 Γ_3T가 없지만 Γ_1T와 Γ_2T를 완벽하게 구하기 위해서는 식 (19)가 반드시 필요하다.

$\[ {\Gamma }_{1T}=\frac{p_{1T}{E}_{1T}+p_{11}{E}_{11}+p_{12}{E}_{12}+p_{13}{E}_{13}+p_{12}{\Gamma }_{2T}+p_{13}{\Gamma }_{3T}}{1-p_{11}} \]$

(17)

$\[ {\Gamma }_{2T}=\frac{p_{2T}{E}_{2T}+p_{21}{E}_{21}+p_{22}{E}_{22}+p_{23}{E}_{23}+p_{21}{\Gamma }_{1T}+p_{23}{\Gamma }_{3T}}{1-p_{22}} \]$

(18)

$\[ {\Gamma }_{3T}=\frac{p_{3T}{E}_{3T}+p_{31}{E}_{31}+p_{32}{E}_{32}+p_{33}{E}_{33}+p_{31}{\Gamma }_{1T}+p_{32}{\Gamma }_{2T}}{1-p_{33}} \]$

(19)

이제 앞에서 구한 식 (2)-(15)의 결과들과 식 (17)-(19)를 바탕으로 하여 최종적으로 식 (16)을 정리하면 다음과 같다.

$\[ {\Gamma }_{\mathit{ST}}=\frac{1}{\lambda }[({\gamma }_R-{\gamma }_U)+e^{\lambda U}({\gamma }_U-{\gamma }_I)-e^{\lambda R}{\gamma }_R+e^{\lambda I}\{e^{\lambda U}({\gamma }_I-{\gamma }_R+e^{\lambda R}{\gamma }_R)\}] \]$

(20)

Ⅳ. 수치 예제

본 장에서는 3장에서의 분석결과를 활용하여 다양한 파라미터들로 이루어진 환경 하에서 최적의 센서 데이터 전송주기 I는 어떠한 경향을 보이는지 살펴본다. 실측 데이터를 기반으로 하기 위하여 상용 무선 통신 모듈 [9]과 모바일 DRAM [10]의 전력 값을 파라미터로 활용하여 γ_I=0.02 와트(watt) , γ_U=0.4 와트(watt)로 설정하였다.

Fig. 4.

Energy overhead ratio f for varying I with respect to λ

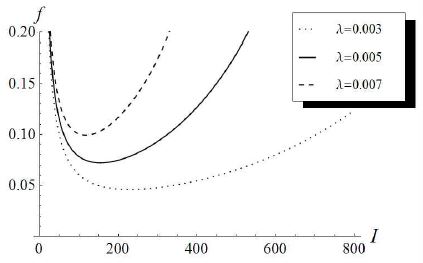
Fig. 4는 결함 발생률 λ와 데이터 전송주기 I에 따른 f의 변화를 나타낸다(식 (21) 참조). 또한, Table 1에서는 Fig. 4와 동일한 환경 하에서 식 (22)를 사용하여 구한 최적 데이터 전송주기 I^*를 λ에 따라 정리하였다. Fig. 4를 보면 Table 1에서 제시된 최적 전송주기 값에서 f가 최소가 되는 것을 확인할 수 있다.

Table 1.

Power-Optimal Data Transmission Interval Values for Various Fault Rates

Fig. 5.

Energy overhead ratio f for varying I with respect to k (γU=kγI)

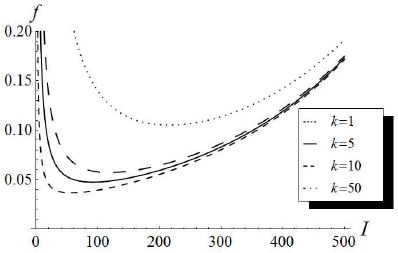
Fig. 5는 센서 데이터를 전송하는 동안 사용하는 에너지 소비량 γ_U와 데이터를 수집하는 동안 사용하는 에너지 소비량 γ_I와의 비율 k에 따른 f의 변화를 나타낸다. 무선인터페이스마다 서로 다른 k값을 가지므로 이 비율을 고려하는 것은 다양한 환경을 반영하는 데 큰 의미가 있다. Table 2에서는 Fig. 5와 동일한 환경 하에서 최적 데이터 전송주기를 k에 따라 정리하였다. Fig. 5를 보면 Table 2에서 제시된 최적 전송주기 값에서 f가 최소가 되는 것을 확인할 수 있다.

Table 2.

Power-Optimal Data Transmission Interval Values for the ratio of γI to γU

Fig. 6.

Energy overhead ratio f for varying I with respect to n (γR = nγI)

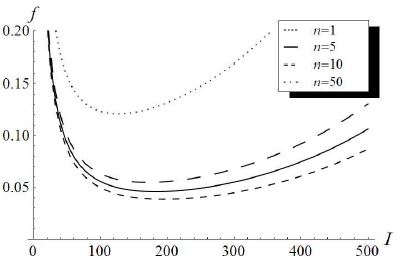
Fig. 6은 f의 변화를 나타낸다. Table 3은 Fig. 5에 주어진 환경 하에서 구한 최적 데이터 전송주기의 값을 n에 따라 계산하여 정리한 것이다. Table 2와 Table 3으로부터 γ_U와 γ_I의 비율 k의 값이 커질수록, γ_R과 γ_I의 비율 n이 작아질수록 더 긴 최적 데이터 전송주기를 가진다는 것을 알 수 있다.

Table 3.

Power-Optimal Data Transmission Interval Values for the ratio of γI to γR

본 장에서는 시스템의 중요한 성능척도라 할 수 있는 센서 결함의 발생률과 다양한 센서 기기들의 사양에 맞추어 분석이 가능하도록 γ_I와 γ_U, γ_R의 비율을 고려하여 수치예제를 보였다.

Ⅴ. 결론 및 추후연구과제

본 연구에서는 무선 센서 기기에서 데이터를 일정 기간 수집(aggregate)한 후 센서 서버로 보내는 환경에서, 확률과정 중 하나인 마코프 체인과 재생 보상 이론을 사용하여 에너지 소비 모델을 개발하였다. 그리고 개발된 모델을 기반으로 전력소비를 최소화하는 센서 데이터 전송주기의 최적해를 구하였다. 또한, 실제 무선통신 장치의 파라미터들을 활용하여 제안한 모델과 최적 전송주기의 성능을 수치예제로 보였다. 본 연구의 결과는 실제 센서 네트워크 시스템의 개발과 적용에 정량적인 예측을 통한 가이드라인을 제공할 수 있다는 데 그 의의가 있다.

본 연구에서는 여러 센서들로 이루어진 네트워크에서 하나의 센서 단말과 센서 서버와의 통신만을 고려하였다. 이를 확장하여 네트워크 전반의 에너지 최적화 문제를 푸는 것도 향후 의미가 있을 것이다. 또한 다양한 환경 파라미터들을 적용하고, 시뮬레이션을 병행하여 실제 시스템을 반영하는 연구를 계획 중이다.

References

• H. Alemdar, and C. Ersoy, “Wireless Sensor Networks for Healthcare: A Survey”, Computer Networks, 54, p2688-2710, (2010). [https://doi.org/10.1016/j.comnet.2010.05.003]
• Amadeus Traveler Tribes 2030 - Building a More Rewarding Journey, Available: http://www.amadeus.com/
• T. Rault, A. Bouabdallah, and Y. Challal, “Energy Efficiency in Wireless Sensor Networks: A Top-down Survey”, Computer Networks, 67, p104-122, (2014). [https://doi.org/10.1016/j.comnet.2014.03.027]
• S. Sasirekha, and S. Swamynathan, “A Comparative Study and Analysis of Data Aggregation Techniques in WSN”, Indian Journal of Science and Technology, 8(26), p1-10, Oct), (2015. [https://doi.org/10.17485/ijst/2015/v8i26/81713]
• H.W. Lee, Queueing Theory, 3rd ed, Sigma Press, (2006), (In Korean).
• S.-H. Lim, S. W. Lee, B.-H. Lee, and S. Lee, “Power-Aware Optimal Checkpoint Intervals for Mobile Consumer Devices”, IEEE Transactions on Consumer Electronics, 57(4), p1637-1645, Nov), (2011. [https://doi.org/10.1109/tce.2011.6131136]
• S.-H. Lim, S. W. Lee, B.-H. Lee, S. Lee, H.W. Lee, “Stochastic method for Power-Aware Checkpoint Intervals in Wireless Environments: Theory and Application”, Journal of Industrial and Management Optimization, 8(4), p969-986, Nov), (2012. [https://doi.org/10.3934/jimo.2012.8.969]
• S.M. Ross, Stochastic Processes, 2nd ed, Wiley, (1996).
• “CW1200:802.11n dual-band WLAN system-on-chip,” Data Sheet, ST Ericsson.
• “Mobile DRAM Power-Saving Features and Power Calculations,”, Technical note, TN-46-12, Micron, May), (2009.
• Wolfram Official Web Site, Available: http://reference.wolfram.com/language/ref/ProductLog.html