High Utility Itemset Mining by Using Binary PSO Algorithm with Database Reduction and OR/NOR Tree construction
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract
High utility itemset mining (HUIM) is a sub-domain of data mining. This differs from frequent itemset mining (FIM), which evaluates both the amount and profit elements of the commodity to uncover profitable commodities rather than just the frequency of occurrences. Traditional HUIM algorithms must manage the exponential growth of the search space when the volume of data or the number of distinct items is large. Heuristic algorithms are an effective alternative to fixing this problem. The binary particle swarm optimization (BPSO) algorithm is a heuristic algorithm that has been used in many fields. This paper proposes a BPSO algorithm with database reduction and OR/NOR tree construction. The database reduction was used to eliminate combinations of low utility items, and the OR/NOR tree construction was used to eliminate inefficient combinations of high utility itemsets (HUIs). It is experimentally demonstrated that the proposed algorithm reduced the running time by 14% and mined more HUIs.
초록
높은 유틸리티 항목집합 마이닝(HUIM)은 데이터 마이닝의 중요한 분야이다. 이는 수익성이 높은 항목을 추출하기 위해 해당 항목의 발생 빈도와 가치를 함께 반영한다는 점에서 단순히 발생 빈도만을 고려하는 빈발 항목집합 마이닝(FIM)과는 차이가 있다. 기존의 HUIM 알고리즘들은 데이터의 용량이 크거나 항목의 수가 많을 경우 기하급수적으로 늘어나는 탐색 공간을 다룰 수 있어야 한다. 휴리스틱 알고리즘들은 이 문제를 해결하는 효율적인 대안이다. Binary Particle Swarm Optimization(BPSO) 알고리즘은 다양한 분야에서 사용되는 휴리스틱 알고리즘이다. 본 논문에서는 데이터베이스 축소 및 OR/NOR 트리 구조를 함께 활용한 BPSO 알고리즘을 제안한다. 데이터베이스 축소는 낮은 유틸리티 점수를 가지는 항목들의 조합을 제거하는 데 활용되었으며, OR/NOR 트리 구조는 높은 유틸리티 항목집합의 비효율적인 조합을 제거하는 데 활용되었다. 본 논문에서 제안한 알고리즘은 수행 시간을 14% 단축시켰으며 더 많은 수의 높은 유틸리티 항목집합(HUI)을 추출함을 실험을 통해 입증하였다.
Keywords:
High utility itemsets, Particle swarm optimization, Database reduction, OR/NOR tree, Data mining키워드:
데이터베이스 축소, OR/NOR 트리, 데이터마이닝Ⅰ. Introduction
Frequent itemset mining (FIM) is a crucial technique in data mining. Frequent patterns refer to the itemset that appear frequently in a database. However, the same item can be purchased multiple times in a single transaction, and each item's profit differs. These factors are not taken into account by frequent itemset mining. To fix these flaws in the frequent itemset, high utility itemset mining (HUIM) is proposed.
HUIM mines the itemset that satisfies certain conditions by a certain strategy. The mining method is required to mine itemsets that are neglected in frequent itemset mining but have high utility values although they are less frequent. For instance, low sales of laptops but high profits, high sales of milk but low profits.
The process of finding all itemsets in the database that utility values no less than a threshold is called utility mining, and the found itemsets are considered HUIs. The utility of an itemset can be measured in practical application scenarios by a variety of factors such as weight, profit, or cost, which can be chosen by the users according to their actual needs. Therefore, in some practical application scenarios, utility mining can be more intuitive for decision assistance.
The search space for the traditional HUIM algorithm is large and takes a long time when the size of the mined database is large, or the number of items contained is very large. Meta-heuristic algorithms can be utilized to solve such problems.
Meta-heuristic algorithms are improvements of heuristic algorithms, which are the product of the combination of randomization algorithm and local search algorithm. Kannimuthu used a genetic algorithm with sorting mutations of minimum utility thresholds to develop the extraction of high utility patterns to mine HUIs [1]. During the planning process, this algorithm requires crossover and mutation to generate the next solution at random. But for this algorithm to find a satisfactory itemset requires a lot of computation in the initial stage, which takes a long time.
Particle swarm optimization (PSO) is another metaheuristic algorithm that is a population-based stochastic optimization algorithm [2]. It finds the optimal solution by adjusting the velocity and position of the particles, guided by individual and global solutions. PSO algorithms unlike genetic algorithms, do not require crossover and mutation operations and hence save time.
The original PSO algorithm was designed used to handle continuous space optimization problems, e.g., to find a function's optimal solution. However, for the case of mining HUIs, there are only two states for each item, i.e., with or without it. To overcome this problem, the binary PSO (BPSO) algorithm was created [3].
With proper changes, the discrete space in BPSO is mapped to the continuous particle motion space. To find the optimal solution, BPSO algorithm uses the standard PSO algorithm's velocity-position update strategy. The particle velocity update formula remains the same, but the individual position can only take one of two values: 0 or 1.
In BPSO algorithm, the transfer function calculates the probability of particle location change. Therefore, when choosing the transfer function, the absolute value of the particle velocity should be considered. The transfer function should provide a larger potential of position change for larger absolute values of velocity. Because a particle's velocity is related to its superiority or inferiority, a higher velocity implies that the particle is further from the optimal solution and vice versa [4].
The original BPSO algorithm used a sigmoid function, also known as an S-shaped function, as a transfer function. The transfer function of BPSO was divided into S-shaped and V-shaped functions by Mirjalili [5]. Experiments with the S-shaped transfer function show that the algorithm lacks local search ability in the later stages. Mirjalili compared the effectiveness of the V-shaped and S-shaped transfer functions on benchmark functions and proved the V-shaped transfer function's superior search abilities on numerous benchmark functions.
In addition, the change of acceleration coefficients of the particles during the particle search also affects the particle search results. There are two types of acceleration coefficients: linear and nonlinear. And Sun's experiments show that the nonlinear method is more precise and steadier when searching for the optimal solution [6].
In the existing studies, most of them are to apply the original PSO algorithm directly in HUIM and only use some approaches to enhance the efficiency of mining during data pre-processing or mining process. These approaches ignore the performance enhancement of PSO algorithm. Therefore, if the ability of the PSO algorithm on HUIM is to be further enhanced an improved PSO algorithm needs to be selected. Furthermore, both PSO algorithms with V-shaped transfer function and nonlinear acceleration strategy have been proven to have stronger search ability. Thus, we used both approaches in the PSO algorithm to enhance the mining ability and accuracy of the algorithm.
However, using these two approaches increases the running time of the algorithm. Therefore, we proposed the BPSO algorithm with database reduction and OR/NOR tree construction to reduce running time while ensuring accuracy.
Traditional utility mining models do not have the downward closure property, so all combinations have to be computed if all HUIs are to be mined. Liu et al. proposed a transaction-weighted downward closure property to reduce the combinations while mining HUIs and reduce the computational effort of the program [7]. Then, based on this property, Lin et al. first find high-transaction-weighted utilization 1-itemsets (1-HTWUIs) in the data. And based on the 1-HTWUIs construction the high-utility-pattern (HUP)-tree to mine the HUIs [8].
Since the heuristic algorithm continuously generates random solutions during the iterative process. Lin et al. proposed the OR/NOR tree, which enables the algorithm to validate random solutions (whether they are combinations that exist in the database) [9]. As only valid random solutions are computed, it can reduce the number of database scans.
The contributions of this paper are that we use V-shaped transfer function and nonlinear acceleration strategy to enhance the search capability of PSO algorithm. And we integrate these two approaches with TWU model to reduce the data and find HUIs. In addition, we adopt OR/NOR tree construction to reduce the number of scans on the database, reduce the computation of invalid particles and shorten the running time.
Experiments demonstrate that database reduction and OR/NOR tree construction effectively improve the efficiency of mining and reduce the running time.
Ⅱ. Related Works
2-1 High Utility Itemset Mining
HUIM is considered an evolution of weighted FIM. In weighted FIM, only the number of occurrences of an item and its weight are counted, but the number of items in each transaction is not taken into account. However, the same commodity may be purchased multiple times in a transaction, and the total profit generated by the transaction cannot be calculated solely based on the profit of a single commodity. As a result, researchers proposed HUIM to maximize the benefits for merchants’ profit while avoiding ignoring those profitable but low support items. It considers the unit profit (the weight of the items) as well as the number of items in the transaction. This scenario does not lend itself well to traditional weighted frequent itemset mining.
Chan [10] was the first to propose the problem of mining HUIs. Subsequently, Yao found HUIs in terms of item amount as an internal utility and profit per unit as an external utility [11]. And he proposed the mining algorithm as a solution to solve this problem.
The core of HUIM is utility. It is decided by two factors, the profit of the item and the number of items in each transaction. And both factors are considered in the calculation of utility. If the utility of an itemset is not less than the minimum threshold set by the user, then the itemset is considered a high utility itemset (HUI).
2-2 Particle Swarm optimization
The particle swarm optimization algorithm was proposed by Kennedy and Eberhart in 1995, which simulates the behavior of a flock of birds searching for food randomly in an area. They want to find the location with the most food, but all the birds do not know the exact location. Each bird searches in the direction it judges, recording the location of the most food it found as it searched and sharing it with the other birds. In this way, the flock knows which location currently has the most food and adjusts its next search direction based on this information during the search.
The PSO algorithm is inspired by this biological population behavior, which is utilized to address the optimization problem. The above-mentioned bird individuals are modeled by particles, and each particle is considered a searching individual in an N-dimensional space. The current position of a particle is a candidate solution to the corresponding optimization problem, and the flight process of the particle is the search process of the individual. The particle's flight velocity can be dynamically adjusted based on the individual's historical optimal position and the population's historical optimal position [3].
The process of PSO can be illustrated as follows:
1. Initialization: Set the number of particles and the upper and lower velocity limits first, then the maximum number of iterations, the position information for the entire search space. Then, on the velocity interval and search space, randomly initialize the velocity and position of each particle.
2. Iteration: Define fitness function, the individual optimal solution (pbest) is the optimal solution found by each particle individually, i.e., the best outcome after calculation by the fitness function. And the global optimal solution (gbest) is the result with the best outcome among these individual optimal solutions. The largest pbest and gbest are then updated and retained, and the pbest and gbest are compared to previous values. Then the particle updated the position based on their own inertia, pbest and gbest.
3. Termination condition: The particle's global optimal solution, as well as its position and velocity, are updated constantly until the termination criterion is met.
The position and velocity of the particle are described as follows during the update of the PSO algorithm:
| (1) |
| (2) |
In Eps. (1) and (2), the number of iterations is denoted by t, and the inertia factor is denoted by w1. The velocity of the id-th particle is denoted by vid, the rand () represents a random number on the range [0,1], and the position of the id-th particle is denoted by xid. For each particle, c1 and c2 represent the individual and social learning elements. They are also known as cognitive acceleration and social acceleration. And individual learning and social learning, on the other hand, influence the local and global search ability of the particle, respectively. If the value of individual learning of the particle is bigger, the local search ability of the particle is stronger. Conversely, if the value of social learning of the particle is bigger, the global search ability of the particle is stronger.
According to Kennedy and Eberhart, the values of c1 and c2 should be set to 2 to balance the search ability of local and global search. However, Ratanweera proposed a linear acceleration strategy in which with the increasing number of iterations, c1 gradually becomes smaller and c2 gradually becomes bigger. It permits the flight velocity of the particle to refer more to its own information at the early stage of the algorithm and more to social information in the later stages. This results in the final result being closer to the optimal solution than the PSO algorithm that uses constant acceleration values [12].
Subsequently, Feng showed experimentally that better results are obtained when using an asymmetric range of variation (c1 decreases from 2.75 to 1.25, and c2 increases from 0.5 to 2.25) [13]. However, the drawback of this method is that it causes the particles always to converge to the local optimal solution in advance. Chen also suggested a nonlinear acceleration adjustment strategy constructed by using arccos function construction to address this issue. And experiments showed that the method improved the convergence for the multi-peaked function and enhanced the ability to search for the global optimal solution [14].
In addition, particle swarm algorithms are also used for data mining of other patterns. To generate association rules for the relationship between sentiment dimensions and design attributes, Jiang proposed a multi-objective particle swarm algorithm [15]. To mine association rules, Indira proposed an adaptive strategy for controlling inertia and learning factors in particle swarm algorithms [16]. Jitendra proposed a method for mining positive and negative association rules. They applied the coding step to positive and negative rules, respectively, in terms of statistical correlation between transaction databases [17].
However, in real-life scenarios, the variables of many problems do not in a continuous interval, but in a discrete variable space. Therefore, Kennedy and Eberhart designed a discrete binary PSO (BPSO) to address the limitations of continuous PSO [3].
The BPSO algorithm converts each particle into a set of binary variables and maps the discrete problem space to the continuous particle motion space. The key step in BPSO is the conversion of real values to binary values of 0 or 1 by means of a transfer function. And the possibility of altering the elements of the position vector from 0 to 1 is defined by transfer functions. Original transfer functions are used to perform probabilistic updates using sigmoid transition functions. The V-shaped transfer function has the advantage over the sigmoid transfer function in that it encourages particles to stay in their current position when the velocity value is low and switch to their complement when their velocity value is high. It makes enhanced local search ability of the algorithm possible, which improves the performance of the BPSO algorithm. Zhang mined the frequent itemsets by the BPSO algorithm with V-shaped transfer function [18].
Ⅲ. Problem Statement
HUIM is the process of finding the itemsets with utility values not less than the threshold value from transaction database. A series of formulas must be used to calculate the utility value. The next sections outline the problem description and related definitions for HUIM.
Let I= {i1, i2, ⋯, in} be a finite itemset, and the item ij (1 ≤ j ≤ n), in this set, each item has uniquely determined profit values p(ij). If the itemset contains k items, it is called a k-itemset. The transaction database includes a transaction table and a profit table. The transaction table includes multiple transactions T = {T1, T2, ⋯, Tm}, where each transaction Td (Td ⊆ T) has a unique identifier d, called TID, and each transaction includes items and their corresponding purchase quantities. Then, depending on the user's preferences, a minimal utility threshold is set as min_threshold according to the user’s preference. It will serve as the foundation for judging HUIs.
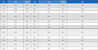
An example is given in Table 1 and Table 2 as a running demonstration for this paper. Table 1 shows the transaction data, with a total of 10 transactions and 6 different items, denoted by a to f, respectively. And Table 2 shows the profit table.
The following are seven definitions for HUI calculations.
Definition 1. The utility value of an item ij, in a transaction Td is denoted as u (ij, Td), which is equal to the quantity of ij in the transaction Td, denoted as q(ij, Td), multiplied by the corresponding profit p(ij) which is defined as
| (3) |
For example, T2 contains four items b, d, e, f, and calculate the utility of item b, u(b, T2)=q(b, T2)×p(b)=5×9=45.
Definition 2. The utility value of itemset X in a transaction Td is denoted as u(X, Td), which is defined as
| (4) |
For example, in transaction T2, the utility values of itemset (bd) is calculated as u(bd, T2)=u(b, T2)+u(c, T2)=45+60=105.
Definition 3. The utility value of an itemset X in a transaction database DB is denoted as u(X), which is defined as
| (5) |
For example, in the whole transaction database, the utility value of itemsets (bc) is calculated u(bc)=u(bc, T1)+u(bc, T6)=117+72+54+48=291.
Definition 4. The total utility value of a transaction Td is denoted as tu(Td) ), which defined as
| (6) |
For example, tu(T1)=u(b, T1)+u(c, T1)+u(d, T1)=117+72+120=309. By the same token, it follows that tu(T2)=250, tu(T3)=306, tu(T4)=196, tu(T5)=302, tu(T6)=102, tu(T7)=158, tu(T8)=198, tu(T9)=235 and tu(T10)=285.
Definition 5. The total utility value of transaction database DB is denoted as TU, which defined as
| (7) |
The total utility value of DB is calculated as TU =309+ 250+306+196+302+102+158+198+235+285= 2341.
Definition 6. HUI is an itemset whose utility is not less than threshold (TU × min_threshold).
Definition 7. In a transaction database DB, there are multiple transactions that contain an itemset, and the sum of the utility values of these transactions is called the transaction-weighted utility of an itemset, denoted as TWU(X).
| (8) |
HUIM is to find the itemsets whose utility values are not less than the threshold from the transaction database and the profit table, where the threshold is set by the user.
Ⅳ. Mining Methodology and Process
In this section, the mining process in conjunction with the PSO algorithm will be described in detail here.
4-1 Particle Encoding
The BPSO mining algorithm is the foundation of the proposed algorithm. The particles are the basic unit of the BPSO algorithm and each particle in the PSO algorithm corresponds to an itemset, i.e., a potential HUIs. The presence or absence of the corresponding item is represented by 1 or 0 in each position of the itemset. As shown in Fig. 1, only the corresponding positions of items (a) and (e) are 1, so the itemset corresponding to particle (10010) is (ae).
4-2 Particle Encoding
The particle evaluation in the BPSO algorithm is dependent on the fitness function results. The utility value of the itemset is represented by the fitness value. In the process of evolution, new particles (potential solutions) are continuously generated, and the utility value of the new particles is calculated by the fitness function, and the merit of the new particles is judged according to the result of the fitness function. The best position of an individual is denoted as pbest and the best position in the population is denoted as gbest. They provide the foundation for particle motion. The fitness function in this algorithm is defined as
| (9) |
Pi is the i-th particle generated. X is the itemset in pi that is set to 1. Then the fitness value of itemset X was calculated, i.e., the utility value. If the utility value is not less than the threshold, it is considered a HUI and added into the set of HUIs.
Take the utility value calculation of itemset (ae) as an example. Itemset (ae) is present in transactions T5, T8 and T10. So the utility value is calculated as u(ae)= u(ae, T5)+u(ae, T8)+u(ae, T10)=62+54+40=156.
4-3 Database Reduction
The length of HUI is determined by the number of high-transaction-weighted utilization 1-itemsets(1-HTWUIs) found during the preprocessing.
The 1-HTWUIs was proposed based on TWU model. 1-HTWUIs are a set of individual items, and the utility value of each item is not less than the threshold.
The proposed algorithm calculates the utility value of each item, then compares it with the threshold and finds the 1-HTWUIs. Then the items that are not 1-HTWUIs in each transaction. This process can reduce a massive set of invalid items. Since HUIM needs to constantly scan the database during the mining process, reducing the dimension of items can reduce the time spent on scanning the database.
Each particle has a fitness value determined by a fitness function. When initialized, every particle is given an initial velocity and position. The particles then change their positions according to the result of calculated fitness values.
Take the database in Table 1 as an example, the minimum utility threshold is set to 0.2 and the total utility of the database is 2341, so the threshold is calculated as follows (2341*0.2=468.2). Compared to the threshold, items with larger utility values are treated as 1-HTWUIs and smaller items are pruned. The discovered 1-HTWUIs are shown in Table 3. From Table 3, we can see that item c does not belong to the 1-HTWUIs, so the information related to item c should be pruned in the database and profit table.
Based on the obtained 1-HTWUIs, the reduced transaction database is shown in Table 4. And the item and the corresponding utility value (quantity multiplied by profit) of the new transaction database are converted into two matrices as shown in Table 5 and Table 6. Then the particle adaptation value is calculated by scanning these two matrices. The original PSO algorithm gives a random value for particle initialization, while this algorithm uses the converted binary matrix as the basis for particle initialization, which has the advantage that each item of the generated particles is from the 1-HTWUIs of the database, which reduces the interference of low utility item.
4-4 Constructing OR/NOR tree
The initialization of particles in the PSO algorithm affects the algorithm's results. The higher the quality of the initial particles, the better the fitness function's outputs, and hence the greater the chance of mining HUIs. Because the preceding generation has an effect on the particles formed during the iterative phase.
The BPSO algorithm, on the other hand, generates random particle combinations. As a result, it is critical to determine whether the combinations are redundant; if the combination does not exist in the database, it is redundant. The algorithm's running time can be reduced by not calculating the utility value of redundant combinations.
As a result, during initialization, it is necessary to build non-redundant combinations using an OR/NOR tree and then check whether the generated combinations exist in the database during iteration.
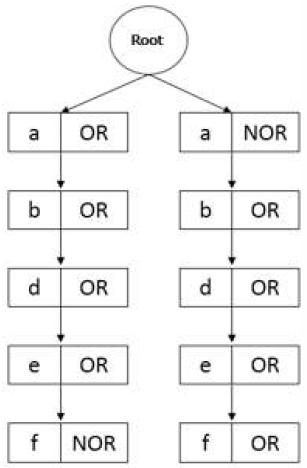
The OR/NOR tree is created by converting the set of maximal patterns into a tree. The maximal pattern is defined in Definition 8.
Definition 8. For a pattern (a), if there is no other pattern in the database that is a superset of (a), then (a) is termed the maximal pattern.
The way of identifying the maximal pattern in the proposed algorithm is to sort the reduced transaction database according to the length of the data. Then start from the longest data as the maximal pattern. Afterward, traverse the database, delete the data of all the subsets of that pattern in the database, and then continue to find the next maximal pattern. Continue to identify the largest pattern of length minus one until all of the data has been traversed. When a new maximal pattern is identified, it is added to the set of maximal patterns.
Then each maximal pattern is converted into a binary itemset in the order of particle encoding. One after the other, the converted binary itemsets are converted into the nodes of OR/NOR tree. The conversion is done by traversing each position of the itemset. It is converted to an "OR" node when the position is 1, and to a "NOR" node when the position is 0. Convert the next itemset after the previous one has been converted. When the position is 1, choose the "OR" node; otherwise, choose the "NOR" node. A new node is formed if a different value exists at a place; otherwise, continue along the node to compare the value at the next position.
Taking the reduced database in Table 4 as an example, the maximal patterns of this database are (abde) and (bdef). First convert (abde) to a binary itemset (11110), corresponding to the generated nodes: {(a,OR), (b,OR), (d,OR), (e,OR), (f,NOR)} Then convert (bdef), which corresponds to the set of binary itemset (01111), , and its converted nodes are {(a,NOR), (b,OR), (d,OR), (e,OR), (f,OR)}. The OR/NOR tree structure constructed through the reduced database in Table 4 is shown in Fig. 2.
During initialization and iteration, the OR/NOR tree generates or verifies particles. When particles are generated via an OR/NOR tree, the particles will choose an OR/NOR tree path at random. When a position is an "OR" node, it can randomly generate 0 or 1. When a position is marked as a "NOR" node, it can only generate 0.
After itemsest generation, the OR/NOR tree can also be used to determine whether the itemsets are redundant. If the current position is 1, the "OR" node must be chosen, and if it is 0, the "NOR" node must be chosen. For example, the OR/NOR tree in Fig. 5 can verify that the itemset (abf) is redundant. Because the itemset's encoded value is (11001), the initial position is 1, hence the (a,OR) node must be chosen. However, because the path's last node is "NOR," (abf) is a redundant combination.
In the iteration process, the OR/NOR tree structure can help prevent redundant combinations. It can check whether the combinations generated exist in the database [1]. When the particle updates its position, it can determine whether the particle is redundant or not based on whether the new particle conforms to the rules of the OR/NOR tree, i.e., whether the new particle is a subset of a certain maximal pattern, because the combinations are constructed based on the set of maximal patterns and the arrangement of the order of items.
When a new particle does not belong to a subset of a maximum pattern, it signifies the new particle does not belong to a subset of a certain transaction in the database. The itemset mined by HUIM must come from the database. If a particle does not follow the rules of the OR/NOR tree, it signifies that the particle's combination is redundant, and the utility value of the particle does not need to be calculated.
4-5 V-shaped Transfer Function
The update formula for the velocity of the BPSO algorithm is still the same as the original PSO algorithm, shown in Eps. (1). And the probability of particle position change is based on the transfer function. The transfer function should be the probability of changing each dimension of the position vector from 0 to 1 and vice versa.
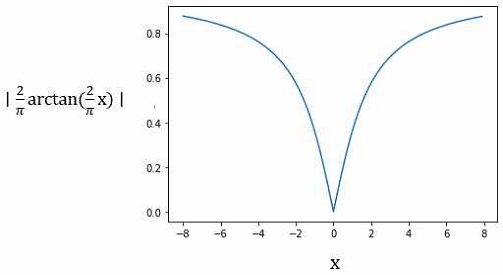
The original transfer function for BPSO position vector update is the sigmoid function. The sigmoid function is a monotonically increasing function, which does not conform to the rule that the probability of its position changing increases with the absolute value of the velocity. The V-shaped function does not force the particle to change its value from 0 to 1. Instead, it maintains the particle at its initial position when the velocity is extremely slow and updates the position to its complement when the particle is moving extremely fast. Because the velocity of the particle in the PSO algorithm represents the quality of the particle. The V-shaped transfer function is shown in Fig. 3, X is the velocity of the particle.
The velocity update formula shows that the velocity of particle would increase as it moves further from the optimal situation. Therefore, when a particle is moving faster, it should be more likely to change its position vector, i.e., updated to the complement of that position vector. So the V-shaped transfer function is chosen as the transfer function of the proposed algorithm.
The V-shaped function is shown in Eps. (10) and Eps. (11), where xid(t)-1 represents the complement of xid(t) and rand() is a random value between 0 and 1.
| (10) |
| (11) |
4-6 Nonlinear Acceleration Strategy
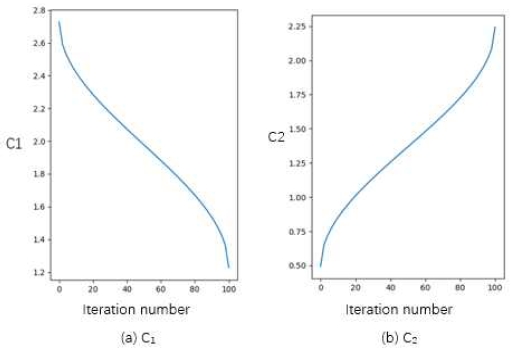
In PSO algorithm, c1 and c2 are the particle's acceleration in Eps. (1). Their values govern how the particle searches, the larger c1, the better the particle's local search ability, and the larger c2, the better the particle's global search ability. Therefore, taking advantage of these two acceleration variations can lead to better results.
For the process of mining HUIs, the ideal state should be to expand the search space of particles at the early stage of the search to obtain the diversity of particles. With more potential solutions at the early stage, it can give more references to particles in the search and enhance the ability to search for global optimal solutions and find more HUIs at the later stage.
To account for the influence of acceleration on the BPSO algorithm, Chen proposed a nonlinear acceleration adjustment strategy based on the arc cos function. [14], as shown in Eps (12) and (13). And the trends of c1 and c2 are shown in Fig. 4. CurrentIterances indicates the current iteration number, and MaxIterances indicates the maximum iteration number, which are parameters pre-set by the user before executing the algorithm. And c1min and c2min are the minimum values of c1 and c2 respectively, and c1max and c2max are the maximum values of c1 and c2 respectively. This strategy brings the particle's search state closer to the ideal state. Therefore, we apply the nonlinear acceleration strategy in the particle velocity update formula to enhance particle diversity and find more HUIs.
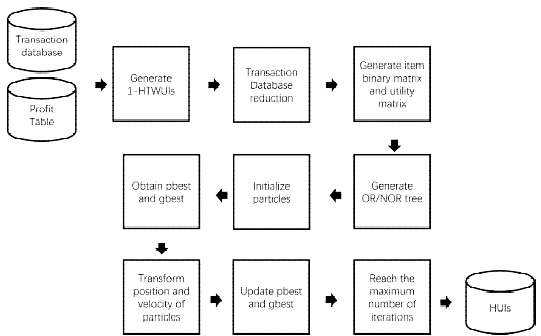
4-7 Mining Process
The proposed mining model of the binary particle swarm algorithm (BPSO) is broken down into four large phases, which contain nine stages. The nine stages of the whole mining process are shown in Fig. 5.
The first phase is data reduction. This phase is to find the 1-HTWUIs and remove the items from the data that are not 1-HTWUIs. The next phase is pre-processing. It entails creating an item binary matrix as well as a quantity matrix. The pre-processing step is concerned with supplying the required data and facilitating the mining process. So in this process, the database is converted into a binary matrix and a quantity matrix.
The third phase is to generate the OR/NOR tree. This phase is to find the maximum pattern of the reduced data and generate an OR/NOR tree based on it. And the last phase is the mining process based on the BPSO algorithm. In this process, the algorithm first gets the initialized particles by OR/NOR tree and assigns random initial velocities. Subsequently, the utility value of each particle is calculated to obtain the pbest and gbest of the particle swarm. Then, in the succeeding iterations, the velocity and pbest of each particle and the gbest of the particle swarm are updated by the V-shaped transfer function and the nonlinear acceleration coefficient strategy. And in the iterative process, the particles with utility values no less than the threshold are added to the set of HUIs. Then repeat the process till the number of iterations reaches the upper limit, and then return the found set of HUIs.
| (12) |
| (13) |
Ⅴ. Experiment and Discussion
This section compared four algorithms: VBPSO algorithm without data reduction and OR/NOR tree, VBPSO-DR algorithm with data reduction only, VBPSO-T with OR/NOR tree only, and VBPSO+ algorithm with data reduction and OR/NOR tree. All experiments are run on a Microsoft Windows 11 computer with an Intel Core i5 3.0GHz CPU and 16GB of RAM. Experiments were conducted on three databases normally used for HUIM: Chess dataset, Mushroom dataset, and Foodmart dataset.
The information of the three datasets is shown in Table 7. The parameters of the particle swarm algorithm were set as follows: the number of particles was set to 20, the velocity range of the particles was set between [-10, 10], and all algorithms were iterated 10,000 times.
5-1 Number of High Utility Itemsets
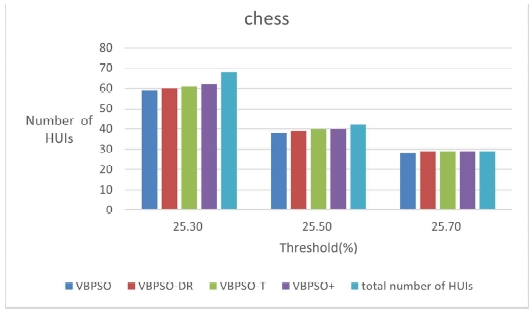
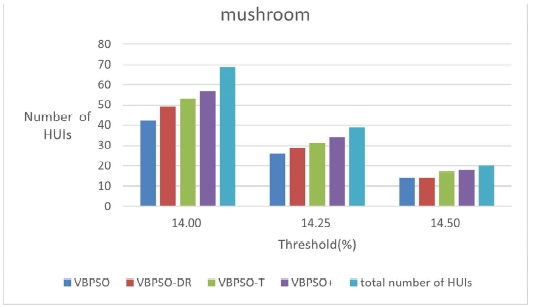
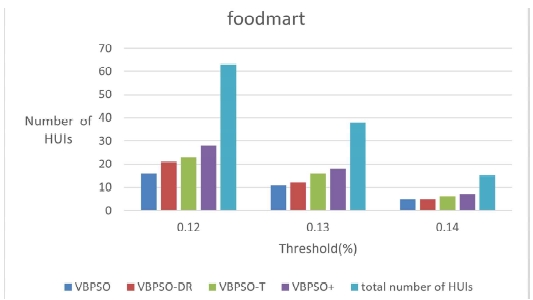
The percentages of HUIs found by the four algorithms are shown in Table 8. The number of HUIs mined by the four algorithms for each of the three datasets is shown Figs. 6 - 8.
From these figures, it is evident that the proposed VBPSO+ algorithm can mine more HUIs compared to other algorithms. It is also evident that as the number of items in the database grows, the percentage of HUI mined by the BPSO algorithm drops, which could indicate the restriction of the PSO algorithm.
5-2 Running Time
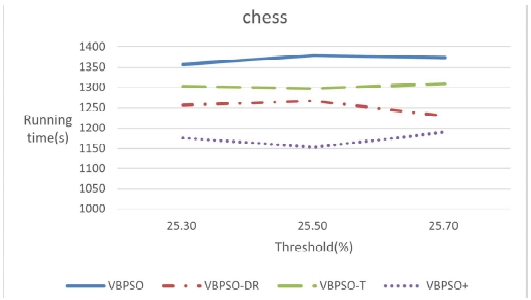
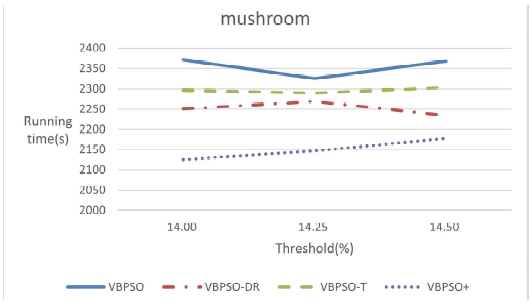
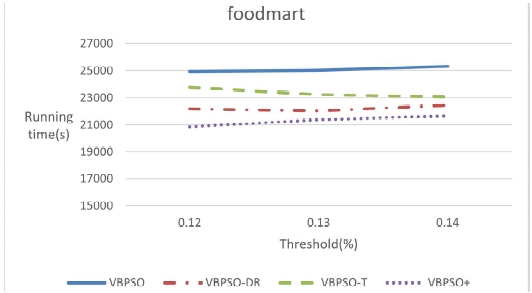
The running times of four algorithms are shown in Table 9. The running times of each algorithm are represented in figures and they are shown in Figs. 9 - 11. The threshold settings for the three datasets in the running time experiments were identical to those used in the mining HUIs experiments.
It is evident that both data reduction and OR/NOR tree reduce the mining time, while the VBPSO+ algorithm combining the two methods has the shortest running time. It confirms the effectiveness of data reduction and OR/NOR tree.
Ⅵ. Conclusion
High utility itemset mining is a critical issue in data mining that can be used to substitute frequent itemset mining in revealing high profit commodities. This paper proposed a new BPSO algorithm, VBPSO+, which is an extension of the original BPSO algorithm with database reduction and OR/NOR tree construction, to mine such itemsets. Several experiments showed that the proposed VBPSO+ can mine more high utility itemsets in less time compared to other algorithms. It reduces the mining time by about 14%.
Furthermore, database reduction is more effective at reducing running time than OR/NOR tree, while the latter is better at effectively mining HUIs. The two methods are combined, and the resulting algorithm VBPSO+ enhances the advantages of both, outperforming VBPSO in terms of mining efficiency and running time.
In recent years, besides the PSO algorithm, some other meta-heuristics algorithms have been proposed. Afterward, we will try to adopt these new meta-heuristics algorithms for HUIM to see if they can improve mining efficiency, e.g., by mining more HUIs or reducing running time.
References
-
Kannimuthu S, Premalatha K, “Discovery of high utility itemsets using genetic algorithm with ranked mutation,” Appl Artif Intell, vol. 28, no. 4, pp. 337–359, 2014.
[https://doi.org/10.1080/08839514.2014.891839]

-
Kennedy J, Eberhart R, “Particle swarm optimization,” IEEE Int Conf Neural Netw, vol. 4, pp.1942–1948, 1995.
[https://doi.org/10.1109/ICNN.1995.488968]

-
Kennedy J, Eberhart R, “A discrete binary version of particle swarm algorithm,” IEEE Int Conf Syst Man Cybern, vol. 5, pp. 4104–4108, 1997.
[https://doi.org/10.1109/ICSMC.1997.637339]

-
Rashedi E, Nezamabadi-Pour H, Saryazdi S, “BGSA: binary gravitational search algorithm,” Natural Computing, vol. 9, no. 3, pp. 727–745, 2010.
[https://doi.org/10.1007/s11047-009-9175-3]

-
Mirjalili S, Lewis A, “S-shaped versus V-shaped transfer functions for binary particle swarm optimization,” Swarm and Evolutionary Computation, vol. 9, pp. 1–14, 2013.
[https://doi.org/10.1016/j.swevo.2012.09.002]

- SUN Xiang, “The influence of dynamic nonlinear acceleration coefficients on PSO,” Computer Engineering & Science, vol. 3, no. 10, pp.131-134, 2011.
-
Liu, Ying, Wei-keng Liao, and Alok Choudhary. "A two-phase algorithm for fast discovery of high utility itemsets." Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, Berlin, Heidelberg, pp. 689-695, 2005.
[https://doi.org/10.1007/11430919_79]

-
Lin, Chun-Wei, Tzung-Pei Hong, and Wen-Hsiang Lu. "An effective tree structure for mining high utility itemsets." Expert Systems with Applications, vol. 38, no. 6, pp. 7419-7424, 2011.
[https://doi.org/10.1016/j.eswa.2010.12.082]

-
Jerry Chun-Wei Lin, Lu Yang. P. Fournier-Viger, T.-P. Hong, and M. V oznak, “A binary PSO approach to mine high-utility itemsets,” Soft Comput, vol. 21, no. 17, pp. 5103–5121, 2017.
[https://doi.org/10.1007/s00500-016-2106-1]

-
Chan R, Yang Q, Shen YD, “Mining high utility itemsets,” IEEE Int Conf Data Mining, pp. 19–26, 2003.
[https://doi.org/10.1109/ICDM.2003.1250893]

-
Yao H, Hamilton H J, Butz C J, “A Foundational Approach to Mining Itemset Utilities from Databases,” SDM, vol. 4, pp. 215-221, 2004.
[https://doi.org/10.1137/1.9781611972740.51]

-
Ratanweera A, Halgamuge S, Waston H, “Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients,” IEEE Transactions on evolutionary computation, vol. 3, no. 8, pp.240-255, 2004.
[https://doi.org/10.1109/TEVC.2004.826071]

- Feng Xiang, Chen Guo long, Guo Wen Zhong, “Setting and experimental analysis of acceleration factor in particle swarm optimization algorithm,” Journal of Jimei University (Natural Science), vol. 11, no. 2, pp.146-151, 2006.
- SL Chen,GR Cai,WZ Guo,GL Chen, “Study on the Nonlinear Strategy of Acceleration Coefficient in Particle Swarm Optimization (PSO) Algorithm,” Journal of Yangtze University (Natural Science Edition) Sci & Eng, vol.04,2007.
-
Huimin Jiang, C. K. Kwong, W. Y. Park & K. M. Yu, “A multi-objective PSO approach of mining association rules for affective design based on online customer reviews,” Journal of Engineering Design, vol. 29, no. 7, pp. 381-403, 2018.
[https://doi.org/10.1080/09544828.2018.1475629]

-
K. Indira, S. Kanmani, “Association rule mining through adaptive parameter control in particle swarm optimization,” Comput Stat.Springer-V erlag Berlin, vol. 30, no. 1, pp. 251-277, 2015.
[https://doi.org/10.1007/s00180-014-0533-y]

-
Jitendra Agrawal, Shikha Agrawal, Ankita Singhai,Sanjeev Sharma, “SET-PSO-based approach for mining positive and negative association rules,” Knowl Inf Syst, vol. 45, no.2, pp.453-471, 2015.
[https://doi.org/10.1007/s10115-014-0795-2]

-
Zhang Zhong-jie,Huang Jian,Wei Ying, “Frequent item sets mining from high-dimensional dataset based on a novel binary particle swarm optimization.” Cent. South Univ, vol. 23, no. 7, pp. 1700-1708, 2016.
[https://doi.org/10.1007/s11771-016-3224-8]

저자소개

2015년 : East China Jiaotong University, China (공학사)
2022년 : 한국해양대학교 대학원 (공학석사)
2022년~현 재 : 한국해양대학교 컴퓨터공학과 박사
※관심분야:데이터베이스, 데이터 마이닝

1985년 : 서울대학교 (공학사)
1987년 : 한국과학기술원 (공학석사)
1995년 : 한국과학기술원 (공학박사)
1997년~현 재 : 한국해양대학교 해사IT공학부 교수
※관심분야:데이터베이스, 데이터마이닝, 빅데이터, 선박 및 해양정보