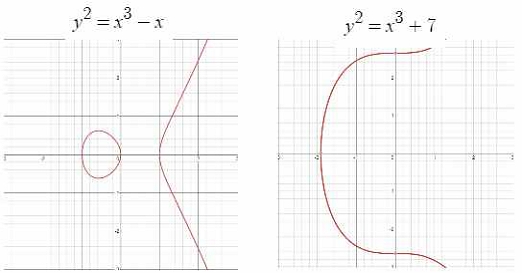블록체인에서 Schnorr 디지털서명의 사용 전망에 관한 연구
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
본 논문은 Schnorr 디지털서명이 기존에 사용되던 ECDSA의 새로운 미래 대안 디지털서명이 될 수 있는지 그 전망에 관한 연구이다. 우리는 현재 블록체인 디지털서명 기술 국내외 사용 현황을 파악하고 Schnorr 디지털서명 체계가 향후 ECDSA를 대체할 가능성이 높은지 그 가능성을 분석하였다. Schnorr 디지털서명의 사용 가능성에 대해 보안성, 효율성, 가단성, 선형성, 배치검증, 다중서명 관점에서 기존 블록체인 디지털서명인 ECDSA보다 좋은 효율을 가지고 있다고 분석하였다. 여전히 대부분 블록체인에서 디지털서명으로 ECDSA가 선호되고 있으며 Schnorr가 ECDSA를 완전히 대체할 거라는 전망은 하고 있지 않다. 하지만, 우리는 Schnorr 디지털서명의 우수성을 통해 블록체인에서 미래 디지털서명으로 ECDSA를 대체할 거라고 본다.
Abstract
This paper is a study on the prospect of whether the Schnorr digital signature can be a new future alternative digital signature of ECDSA that was previously used. We identified the current use of blockchain digital signature technology at home and abroad and analyzed the possibility of whether the Schnorr digital signature system is likely to replace ECDSA in the future. It was analyzed that the usability of Schnorr digital signatures has better efficiency than the existing blockchain digital signature ECDSA in terms of security, efficiency, malleability, linearity, batch verification, and multi-signature. ECDSA is still preferred as a digital signature in most blockchain, and it is not expected that Schnorr will completely replace ECDSA. However, we believe that the excellence of Schnorr digital signatures will replace ECDSA with future digital signatures in blockchain.
Keywords:
Blockchain, Digital Signature, ECDSA, Ethereum, Schnorr키워드:
블록체인, 디지털서명, 이더리움Ⅰ. 서 론
비트코인[1]은 영향력을 계속해서 확장해나가고 있으며 전통 금융권에서조차 가치 저장 수단으로 인정받고 있다. 이미 여러 나라에서 비트코인이 보여준 블록체인 기술의 가능성과 새로운 모습의 전자결제 시스템은 디지털 세상에 거대한 변화를 가져오고 있다. 특히, 세계적으로 비트코인에 관심이 급증하면서 블록체인 연구의 기회가 많아지며 발전에 속도가 붙었다. 블록체인은 2015년 비탈릭 부테린(Vitalik Buterin)이 개발한 이더리움(Ethereum)[2]이라 불리는 2세대 블록체인 플랫폼을 시작으로 다양한 기술을 접목하여 급속도로 발전하고 있으며 스마트컨트랙트(Smart Contract) 같은 블록체인에서 응용할 수 있는 기능들을 구현하기 위한 방향으로 연구되고 있다. 블록체인에서 디지털서명과 스마트컨트랙트는 밀접한 관계가 있다. 현재는 이더리움 클라이언트 소프트웨어에 디지털서명 기능이 내재되어 있지만, 초기 이더리움 개발 시에는 디지털서명 구현을 스마트컨트랙트로 만들었다. 스마트컨트랙트란 계약 당사자가 사전에 협의한 내용을 미리 프로그래밍하여 전자 계약서 문서 안에 넣고, 그 후 계약 조건이 충족되면 자동으로 계약 내용이 이행되도록 하는 시스템이다[3].
본 논문은 현재 블록체인 디지털서명을 분석하고 새로운 디지털서명 대안으로 Schnorr 디지털서명 방법을 제안한다. 현재 블록체인 디지털서명 시스템은 어떻게 구성되어 있으며 어떠한 암호학적 배경을 사용하여 구현되어있는지를 조사한다. 배경지식 및 관련 연구에서는 디지털서명, SHA-256 해시함수, 타원곡선암호, 이산로그문제, secp256k1 타원곡선, ECDSA(Elliptic Curve Digital Signature Algorithm)를 간략하게 설명한다. 블록체인 디지털서명에 필요한 기본 SHA-256 해시함수와 암호화 배경인 타원곡선암호의 핵심 요소인 이산로그문제를 설명하고 타원곡선과 디지털서명 알고리즘을 조사했다. 본론에서는 이러한 디지털서명들이 실제 블록체인 업계에서는 얼마나 사용되고 있는지를 파악한다. 즉, 블록체인 네트워크에 필요한 디지털서명을 어떤 것을 사용하고 있는지 그 동향을 파악했다. 대부분의 블록체인 업체는 디지털서명 체계로 이더리움에서 채택하여 사용하고 있는 ECDSA를 채택하고 있었다. 현황표는 현시점 시가총액 20위권 안에 들어가는 블록체인 암호화폐들의 디지털서명 사용 현황을 표로 정리했다. 현재는 Schnorr가 ECDSA를 완전히 대체할 수 있을 거라는 전망은 크지 않다. 여전히 ECDSA를 사용하고 있는 업체는 많으며 Schnorr의 장점에 대한 인식이 좋아지고는 있지만 ECDSA의 명성에 비하면 아직 한참 부족하다. 그러나 우리는 Schnorr 디지털 서명이 보안성, 효율성, 가단성, 선형성, 배치검증, 다중서명 거의 모든 면에서 ECDSA보다 강점을 갖고 있다는 걸 조사했다. 본 논문은 Schnorr 서명이 ECDSA를 대신하는 미래 디지털서명 대안으로 그 사용 가능성이 높다는 것을 연구했다[2, 3].
Ⅱ. 디지털서명 배경지식 및 관련연구
2-1 디지털서명
디지털서명[4]이란 첨단 기술로 보안이 강화된 전자서명의 한 종류로서, 개인키와 공개키를 이용한 전자서명이다. 블록체인에서 기록되는 데이터의 보안 및 무결성을 보장하는 중요한 요소 중 하나이다. 디지털서명을 제공하기 위하여 처음으로 출시된 소프트웨어는 1989년에 RSA 알고리즘을 사용하여 제작되었다. 참고로, 현재 흔히 사용하고 있는 디지털인증서는 신뢰할 수 있는 제3자의 의해 인증하는 방법으로 디지털서명과는 다른 개념이다. 현재는 처음 사용하였던 RSA 암호기법보다는 타원곡선암호기법이 효율성을 인정받아 사용이 더 많이 되는 추세이다. 디지털서명의 기능에는 중요한 특징이 있다. 첫 번째는 위조방지(무결성)로 제3자가 디지털서명을 위조할 수 없다. 두 번째는 부인방지로 송신자는 자신의 서명된 트랜잭션을 부인할 수 없다.
2-2 SHA-256 해시함수
SHA-256 해시함수[5]란 다양한 길이를 가진 데이터를 고정된 길이를 가지는 데이터로 매핑하는 함수이다. 블록체인에서 SHA(Secure Hash Algorithm) 해시함수는 암호화를 위한 핵심 기술이다. 특징으로는 무결성과 보안성을 가져 암호화된 해시값은 해커라 해도 쉽게 복호화가 불가능하다. SHA-256 해시함수는 2015년에 미국 국립 표준기술연구소(NIST: National Institute of Standards and Technology)가 승인하여 발표한 SHA-1, SHA-2 해시함수에 내재하는 보안 취약점을 개선하고 개발된 암호화 해시 알고리즘이다. 정확한 명칭은 SHA3-256이고 Keccak-256 해시함수라고도 불린다. 평균적으로 SHA-3가 SHA-2보다 4배 정도 빠르고 어떤 플랫폼에서도 좋은 효율성을 보인다.
2-3 타원곡선암호 (ECC: Elliptic Curve Cryptography)
블록체인 디지털서명의 암호학적 배경은 타원곡선암호이다. 타원곡선암호는 유한체 필드 위에서 타원곡선의 대수적 구조를 기반으로 한 이산로그문제에 착안해서 만들어졌다. 타원곡선의 방정식 형태는 수식 (1)로 표현하며 이러한 방정식의 표현을 바이어슈트라스 식(Weierstrass equation) 형태라고 부른다.
| (1) |
캐나다의 써티콤(Serticom)이 설립한 SEC(Standards for Efficient Cryptography)단체는 타원곡선암호가 널리 적용되도록 표준화 정보를 제공한다. 이러한 타원곡선은 매개변수가 필요한데 이 매개변수 선택은 신중하게 이루어져야 한다. 그 이유는 이 매개변수에 따라서 사용되는 타원곡선이 결정되기 때문이다. 타원곡선의 예시를 그림 1에서 확인할 수 있다. 이 매개변수 값을 선택하는 다양한 방법이 있는데, 예를 들면, 무작위로 생성되거나 혹은 생성되지 않을 수 있다. 검증 가능한 랜덤 매개변수를 선택할 때 랜덤 곡선이 아닌 곡선은 일반적으로 특정한 방식으로 만들어진다[6].
| (2) |
효율적인 연산을 보장하기 위해 이러한 특정한 방식을 포함하는 표준화된 타원곡선의 유형이 있다. 수식 (2)에서 볼 수 있는 T(Tuple)는 타원곡선에 필요한 6가지 매개변수를 식으로 표현한 튜플이며 그 매개변수를 하나씩 설명하겠다. p는 타원곡선의 유한체 필드의 경계를 의미한다. a, b는 수식 (1)에서 유한체 필드 타원곡선의 형태를 결정하는 계수이다. G는 타원곡선 위에 존재하는 생성자 점이다. n은 G의 subgroup을 순환해서 생성하는 값이다. h는 cofactor로써 서명에 필요한 매개변수이다[7].
2-4 이산로그문제 (DLP: Discrete Logarithm Problem)[8]
타원곡선암호는 이산로그문제 개념을 기반으로 사용한다. DLP는 xk = y 에서 k 정수를 결정하는 문제이다. 즉 k = logxy 값을 찾는 것이다. 일반적으로 DLP는 생성자 점 G에 의해 정의된다. 타원곡선암호를 기반으로 하는 보안암호 시스템은 타원곡선이산로그문제(ECDLP: Elliptic Curve Discrete Logarithm Problem)를 통해 정의된 DLP의 난이도에 따라 그 보안성이 결정된다. k 가 수백의 비트를 가지는 정수일 때 이것은 비현실적으로 어려워진다. ECDSA에서 주로 사용하는 secp256k1 타원곡선은 DLP를 해결하기 위한 시간복잡도가 O(2256) 로 매우 큰 숫자이다. 타원곡선암호의 주요 이점은 암호키 크기가 작다는 것이다. DLP 난이도는 어렵지만, 보안 수준은 동일하게 가져가며 저장 및 전송 요구사항은 줄일 수 있다. 타원곡선의 알고리즘 실행시간에서 타원곡선 스칼라 곱셈이 밀리초(milliseconds) 단위로 일정한 시간이 필요하다. 이것을 ECDLP로 대략 계산을 해보았을 경우 1028 년이라는 시간이 필요하다. 오늘날의 슈퍼컴퓨터로도 계산이 실현 불가능하다. 이러한 이유로 DLP는 오늘날 여러 공개키 암호 시스템들의 핵심이다.
2-5 secp256k1 타원곡선[6, 7]
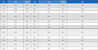
이더리움에서 디지털서명을 위해 사용하고 있는 타원곡선은 secp256k1이라는 이름을 가진 곡선이다. 그 정의를 설명하면 sec 는 Standards for Efficient Cryptography 단체를 나타낸다. p는 Parameters로 유한필드의 경계 크기를 나타낸다. p는 비트 단위로 길이를 나타내는 숫자 256bit 다음에 나온다. k는 Koblitz 타원곡선의 줄임말이며 검증 가능한 무작위 사용을 나타내는 r (random)과는 구별된다. 마지막으로 타원곡선의 분별을 위해 구분하는 시퀀스번호 1번이다. secp256k1 타원곡선은 효율성을 보장하기 위해 랜덤하지 않은 특별한 방법으로 구성되어있으며 y2 = x3 + 7 식을 가진다. secp256k1 타원곡선 구성을 위한 매개변수는 표 1과 같이 정의한다[8].
2-6 ECDSA (Elliptic Curve Digital Signature Algorithm)[2]
타원곡선 디지털서명 알고리즘(ECDSA)은 미국표준기술연구소(NIST)에서 발표한 전자서명 표준을 적합한 타원곡선과 키 쌍의 계산, 전자서명을 지명하고 있으며, 1998년 미국표준협회(ANSI: American National Standards Institute)에서 ECDSA를 표준화해 연방 정보처리표준(FIPS: Federal Information Processing Standards)에 의해 승인되었다. 대표적으로 비트코인과 이더리움에서 주로 사용되고 있고, 해시함수는 SHA-256 함수를 사용하며 타원곡선은 secp256k1을 사용한다. 현재는 수많은 블록체인 플랫폼에서 채택하고 사용 중에 있는 디지털서명 알고리즘이다.
Ⅲ. 블록체인 디지털서명 국내외 동향
현재 블록체인 업계에서는 디지털서명을 어떻게 무엇을 사용하고 있는지 그 현황을 표 2에 정리하였다. 표의 구성은 블록체인 암호화폐별로 출시일, 해시함수, 타원곡선, 디지털서명, 특징을 조사했다. 대부분의 블록체인 업체에서 타원곡선암호를 사용 중이었고 그중에서도 ECDSA 디지털서명 체계를 채택 중이다. 표는 현시점으로 시가총액이 7조원 이상이며 세계 20위권 안에 들어가는 암호화폐 중에서도 현재 활발히 거래되어 사용량이 많은 대표적인 업체들만 정리하였다.
비트코인은 사토시 나카모토(Satoshi Nakamoto)에 의해 2008년에 출시되었으며 처음으로 암호화폐 개념을 만든다. 이때 암호학적 배경을 ECDSA로 채택하고 해시함수는 SHA-256을 사용하며 타원곡선은 secp256k1을 처음 사용한다. 그 후 수많은 블록체인 플랫폼에서 비트코인 디지털서명을 기반으로 체계를 구축한다[1].
이더리움은 비탈릭 부테린(Vitalik Buterin)에 의해 2015년에 출시되었으며 해시함수는 SHA-256, 타원곡선은 secp256k1, 디지털서명체계는 ECDSA를 채택 중이다. 특징으로는 오늘날 블록체인을 대표하는 플랫폼 중 하나라는 것이고, 스마트컨트랙트, EVM 등 2세대 블록체인 플랫폼이 시작된 암호화폐이다[2].
카르다노(Cardano)는 찰스 호스킨슨(Charles Hoskinson)와 제러미 우드(Jeremy Wood)가 2017년에 출시했으며 ADA라는 암호화폐를 사용한다. 해시함수는 SHA-512, 타원곡선은 Curve25519, 디지털서명 체계는 Ed25519를 사용 중이다. 특징으로는 Edwards 타원곡선을 사용한다는 것이고 미래에는 BLISS-B 디지털서명을 통합하여 양자 컴퓨터에 저항 가능한 서명을 추가하는 계획을 갖고 있다[9, 10].
솔라나는 아나톨리 야코벤코(Anatoly Yakovenko)가 2020년인 최근에 출시했으며 디지털서명 체계는 이더리움 기반으로 ECDSA를 사용한다. 특징으로는 리눅스 커널 커뮤니티에서 만든 가상머신인 BPF(Berkeley Package Filter)를 사용한다는 것이다. 핵심기술로는 역사증명(Proof of History)을 합의 알고리즘으로 채택하고 있다[11].
폴카닷은 이더리움 공동창시자인 개빈 우드(Gavin Wood)가 2020년인 가장 최근에 만들었으며, 해시함수는 Blake2b를 사용하고, 타원곡선은 sr25519, 디지털서명 체계는 Schnorr 서명을 사용 중이다. 특징으로는 서로 다른 블록체인을 연결하는 인터체인 프로젝트이다[12].
크립토닷컴체인은 크리스 마자렉(Kris Marszalek)과 바비 바오(Bobby Bao)가 2016년 모나코라는 이름으로 처음 출시했고 그 후 이름을 변경해 2018년에 발행되었다. 디지털서명 체계는 이더리움 기반으로 ECDSA를 사용한다. 특징으로는 자체적인 API를 운영하고 크로노스 메인 네트워크(Cronos Main net)를 따로 사용하여 이더리움 네트워크와 호환되게 하였다. 전자결제 블록체인 플랫폼이다[13].
트론은 저스틴 선(Justin Sun)이 2017년에 출시했으며 디지털서명 체계는 이더리움처럼 ECDSA를 사용한다. 특징으로는 이더리움 블록체인에서 독립하여 자체적인 네트워크를 구성하였다.
또한, 트론은 EVM을 사용하지 않고 따로 트론가상머신(Tron Virtual Machine)을 사용한다[14].
표 2를 보면 대부분의 블록체인 암호화폐들은 이더리움에서 사용 중인 ECDSA 디지털서명 체계를 사용한다. 타원곡선은 secp256k1이며 해시함수는 SHA-256을 사용 중이다. SHA-256은 Keccak-256 해시함수라고도 불린다. 현재 다른 디지털서명 체계를 채택하고 있는 블록체인들을 보면 카르다노는 Ed25519 디지털서명을 채택하고 Edwards 타원곡선을 사용한다. 표 2의 블록체인 업체 중에 가장 최근 출시 된 폴카닷만이 Schnorr 디지털서명을 채택 중이었다. 최근에서야 Schnorr가 여러 가지 측면에서 블록체인에 좋은 강점들을 가져다줄 수 있다는 인식이 생겼지만, 여전히 대부분 업체에선 ECDSA 사용을 선호하며 해외의 몇몇 업체만 Schnorr를 채택 중이고 국내에선 단 하나의 사례도 찾기 힘들 정도로 거의 모든 블록체인 업체가 ECDSA를 사용 중에 있다.
Ⅳ. 블록체인에서 Schnorr 디지털서명 사용 전망
Schnorr 디지털서명은 비트코인 코어 개발자인 피터 윌러(Pieter Wuille)가 비트코인 개선 제안(BIP: Bitcoin Improvement Proposals) 형태로 공식 제안한 문서에 포함된 내용이다. 현재는 ECDSA가 표준화가 잘 되어있어 많이 채택되는 반면에 Schnorr 디지털서명은 지난 몇 년 동안 특허 문제가 있었기 때문에 사용 전망이 좋지 않았다. 하지만, Schnorr 서명이 보안성, 효율성, 가단성, 선형성, 배치검증, 다중서명 관점에서 ECDSA보다 좋은 효율을 낼 수 있다는 점에서 미래 대안 디지털서명으로 사용될 전망이 높다고 본다[15].
- • 보안성: Schnorr는 수학적 증명이 가능하지만, ECDSA에는 그 증명이 존재하지 않는다.
- • 효율성: Schnorr가 ECDSA보다 더 적은 크기의 서명을 사용하고 역함수 계산이 없기 때문에 함수 계산의 속도 측면에서 효율성이 더 좋다.
- • 가단성(Malleability): ECDSA는 가단성이기 때문에 적응형 공격 메시지에 대해 위험성이 있지만 Schnorr는 비가단성으로 그 위험성이 없다.
- • 선형성: Schnorr만이 가지고 있는 특성이며 동일한 메시지에 대한 여러 사용자의 서명을 다르게 하면서 하나의 단일서명으로 검증이 가능하다.
- • 배치검증: Schnorr의 선형성 특성을 이용하여 블록 내의 있는 모든 서명을 한 번에 동시 검증이 가능하게 만든다.
- • 다중서명: Schnorr는 다중서명을 일반적인 단일서명으로 사용이 가능해 서명 크기가 작고 속도 또한 빠르다.
표 3에 Schnorr 디지털서명을 사용하기 위한 BN(Barreto-Naehrig) 타원곡선을 구성하기 위한 매개변수들을 표로 정리하였다[16, 17].
Schnorr Signing 알고리즘을 설명하겠다. 그림 2를 보면 입력값으로 메시지와 q (개인키)를 가진다. k 계수에서 개인키와 메시지를 Keccak-256 해시함수로 해시화하고 q에서 생성자 점을 타원곡선 점 곱셈을 통하여 공개키 (x, y) 좌표 2개를 얻는다. Schnorr 디지털서명에 필요한 32 bytes 계수 e=hash(kG∥Q∥M) 를 구하고 s = k - eq 가 되도록 한다. 결과 값으로 공개키, s, e를 출력한다.
Schnorr Verification 알고리즘을 설명하겠다. 그림 3을 보면 입력값으로 메시지와 Q(공개키)를 가지며 그림 2 알고리즘에서 결과 값으로 나온 s, e 서명 계수를 가진다. 공개키가 무한대 값을 가지거나 타원곡선 위에 존재하지 않는다면 실패한다. kG = sG + eQ 값을 만들고 입력값으로 받은 e 서명계수와 e = hash(kGQ∥M)로 해시화한 한 결과 값을 비교하여 같으면 성공하고 다르면 실패하게 된다. 검증 순서는 아래의 수식 (3-5)과 같은 식으로 이루어진다.
| (3) |
| (4) |
| (5) |
4-1 보안성
ECDLP가 어렵다고 가정한 Random Oracle Model에서 Schnorr 서명은 Generic Group Model이 필요하고 이것을 통해 일반적인 보안을 입증할 수 있게 된다. 하지만, 앞서 말했듯이 보안 증명에는 Generic Group Model이 필요한데 ECDSA는 랜덤 모델이 아니기 때문에 일반적 모델이 존재하지 않는다. Schnorr 서명은 충분히 임의의 해시함수가 제공되고 이 보안 설계는 ECDSA가 가지고 있는 문제점인 취약 공격에 대하여 Schnorr의 보안이 좋은 이유 중 하나이다. Schnorr는 일반적으로 미국 국립표준연구소(NIST)에서 표준을 발표한 P-256 타원곡선을 많이 사용하며 SEC 단체에서 표준을 발표한 secp256r1 타원곡선도 사용하는 편이다[20-22].
4-2 효율성
ECDSA는 v(6,7,8bytes), r(32bytes), s(32bytes) 서명 계수를 갖고 70-72bytes(DER encoding)를 디지털서명으로 사용한다. Schnorr는 s(32bytes), e(32bytes) 서명 계수를 갖고 디지털서명으로 고정된 64bytes 크기를 사용한다. ECDSA는 일반적으로 공개키 복구를 지원하기 위한 recovery parameter가 포함되고, Schnorr는 서명에 x 좌표 하나에 y 좌표를 가지기 때문에 recovery parameter 없이 공개키 복구가 가능해진다. 또한, ECDSA는 계산과정에 타원곡선 역함수 계산과 스칼라 곱셈과 같은 무거운 연산이 많이 들어가 있지만 Schnorr는 상대적으로 적어 연산이 더 빠르다. 서명 데이터가 블록체인에서 차지하는 크기를 줄일 수 있다는 것은 더 많은 거래가 블록에 포함될 수 있으며 사용 수수료가 낮아지는 걸 의미한다. 이더리움 같은 경우 스마트컨트랙트 기능과는 상관없이 오로지 크기에 따라 gas 요금이 정해지기 때문에 크기는 굉장히 중요한 사안이다. 블록체인의 특성상 시간에 비례해 전체 네트워크 블록의 크기가 계속 커지기 때문에 각 블록크기를 적게 사용하는 건 단순하지만 블록체인에 굉장히 중요하다[15, 18, 19].
4-3 가단성 (Malleability)
ECDSA는 가단성으로 위험성이 있지만 Schnorr는 비가단성이므로 가단성에 의한 위험은 없으므로 신뢰성 측면에서 Schnorr가 더 우수하다. 블록체인에서 가단성 문제란 일정한 조건 메시지와 공개키가 있으면 개인키에 접근하지 않고도 제3자가 사용 가능한 것을 가리키고 이 문제는 BIP62에서 정식 논의되었다. Schnorr는 특정 k 계수 값이 필요하기 때문에 s, e 서명 계수 결과 값만 안다고 유효하지 않습니다. 더 자세히 보면, ECDSA에서 서명 (r, s)는 (r, -s)로 대체될 수 있다. 왜냐면 이것은 원본 메시지이고 동등한 서명으로 인지하기 때문이다. 그 말은 제3자가 개인키에 대한 액세스 없이 기존의 유효한 서명을 변경할 수 있음을 뜻한다. 그 위험성은 수식 (6-10)과 같으며 K, - K 는 같은 x 좌표를 사용하게 된다[18, 19].
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
4-4 선형성
Schnorr의 핵심적인 장점은 선형성이다. 여러 사용자가 동일한 메시지에 서명할 경우, 이들 메시지의 합계 서명은 합계의 시작 메시지 위에 유효한 서명이다. 이러한 구조는 ECDSA에선 안전하지 않지만 Schnorr는 가능하다. Adaptor 서명은 앤드류 폴스트라(Andrew Poelstra)의 혁신적인 아이디어인 소위 스크립트 없는 스크립트의 구성 요소이다. 주요 목적은 스크립트 언어가 없는 시스템에 훨씬 더 많은 유연성을 도입하는 것이다. Adaptor 서명은 선형성 특성을 활용한다. 이 도구는 이더리움 스크립트가 아닌 서명을 통해 거래가 원자적으로 이루어질 수 있는 교차 체인 원자 스와프 및 결제 채널에 상당한 영향을 미칠 수 있다. 이는 온체인이 일반적인 단일 서명자 트랜잭션과 동일하게 보이면서 프라이버시와 효율성을 크게 향상시키는 트랜잭션에서 나타난다. 즉, 트랜잭션이 작을수록 수수료가 낮아지고, 블록체인 크기가 작아지고, CPU 요구량이 낮아지고, UTXO(Unspent Transaction Outputs) 집합인 미사용 트랜잭션 출력들이 RAM에 저장되는 게 줄어든다.
Adaptor 서명의 핵심은 비밀 논스값인 k에 랜덤 값 t의 타원곡선 점인 T를 추가하는 것으로부터 나온다. 여기서 k는 여전히 k + t 대신 비밀 논스값으로 간주한다는 점이다. 이것은 잘못된 서명을 초래한다. 그러나 이 구조 덕분에 비밀 정수 t를 알 수 있다. Adaptor 서명에 사용되는 공용키와 동일한 메시지에 유효한 서명인 경우 A와 B를 예를 들겠다. B를 생성하려면 메시지와 그의 개인키를 입력할 때 그림 4에 표시된 대로 진행한다. A는 다음과 같이 K가 K+T와 같은지 여부를 확인하고 실패한다. 이것은 비밀 논스값 k가 t로 상쇄되지 않았기 때문이다. 여기서 서명이 유효하지는 않지만, A는 유효한 서명인지는 확인할 수 있다. 수식 (11)를 이용하면 확인할 수 있다.
| (11) |
A는 s를 가지고 있기 때문에 이 검증은 가능하다. QB 는 주어진 x 좌표로부터 T와 K+T를 재구성할 수 있어 여기서 K를 얻는다. 이것은 ECDLP의 어려움 탓에 t를 찾을 수 없어 프라이버시가 계속 보장된다. 이제 B가 A에 유효한 서명을 준다. 이번에는 K+T = e 검사가 성공할 것이다. A는 이 유효한 서명과 이전에 받은 Adaptor 서명을 통해 그 값의 차이를 취하는 것만으로 랜덤 값인 t를 수식 (12) 처럼 즉시 복구할 수 있다.
| (12) |
4-5 배치검증
Schnorr가 선형성을 가지기 때문으로 한 블록 내의 서명을 동시에 검증이 가능하다. 이것은 여러 검증 식을 하나로 더해서 수행해도 아무런 문제가 없다. 이렇게 하면 타원곡선 스칼라 곱셈 횟수를 줄일 수 있다. 표준화된 ECDSA 공식은 개별에 비해 배치에서 더 효율적으로 검증될 수 없다. Schnorr로 전환하면 일괄 검증이 가능하다. 블록을 검증할 때 여러 서명을 검증해야 하기 때문에 이것은 중요한 기능이 될 수 있다. 다만, 검증이 실패할 경우 어떤 서명이 실패했는지에 대해서는 상관하지 않고 블록 전체를 거부한다. 시스템이 많은 수의 서명을 확인하는 것은 매우 일반적이며, 특히 암호화폐가 널리 채택되고 있는 오늘날에는 더욱 그러하다. 우리가 선택한 공식에서 서명을 검증할 때 가장 무거운 연산은 두 개의 타원곡선 스칼라 곱셈이다. 이것을 (K, s) 표현을 사용하여 서명 작업을 확인할 수 있다. 먼저 해시 연산을 수행한 다음 타원곡선 연산을 수행하는 것이다. 이것이 배치 검증 알고리즘을 사용하여 일괄 검증할 수 있는 핵심 성분이다. K = sG + hash(bytes (K)∥Q∥M)Q 인 경우 서명 (K, s)가 유효하다는 것을 확인했다. 따라서 두 개의 유효한 서명 (K0,s0), (K1,s1)을 수식 (13-14)에서 확인하는 과정은 아래와 같다[18, 19].
| (13) |
| (14) |
곱셈 이전의 s 값을 집계할 수 있다. 이 접근 방식은 스칼라 곱셈 수를 서명 당 1개, 집계된 s에 대해 1개로 줄인다. 하지만, 만약 공격자가 서로 취소하는 일련의 서명을 생성하면 문제가 될 수 있다. 공격자는 배치 유효성 검사가 성공할 수 있기 때문에 네트워크가 유효하다는 것을 알 수 있다.
4-6 다중서명
Schnorr의 다중서명에서의 이점은 일반적인 단일서명 거래로 블록체인 네트워크에 표시된다는 것이다. 기존의 다중서명이 서명자 수가 증가함에 따라 공간 크기와 검증시간이 비례적으로 늘었던 문제점을 해결할 수 있다. 일반적으로 Schnorr는 다음과 같은 암묵적 다중서명 체계를 제시한다. 단일 메시지에 서명하고 싶은 사용자는 각자 서명할 수 있다. 최종 서명은 부분 서명의 합계이다. 그런 다음 공개키의 합계와 비교하여 서명을 확인할 수 있다. 특히, 벨라레-네븐(Bellare-Neven) 알고리즘과 함께 사용하여 독특한 공동을 연관시킬 수 있다는 것이다[23]. 단일 집계된 공개키에 대해 다중 데이터를 검증할 수 있으므로, 제3자의 경우 더 큰 개인정보 보호로 이어진다. Bellare-Neven 체계는 특정 시스템에 의존하는 rogue key 공격을 방지한다. 다중 공용키 통신이 필요 없는 대역폭 개선, 일반 공개키와 통합 공개키를 구별할 수 없다는 개인정보 보호가 특징들이다[24, 25].
Ⅴ. 결 론
본 논문에서 우리는 타원곡선암호에 기반을 둔 블록체인 디지털서명 체계가 현재 블록체인 업계에서는 무엇을 어떻게 적용되어 사용 중인지 그 현황을 파악했다. 기존의 블록체인 디지털서명인 ECDSA와 조금씩 인식이 좋아지고 있는 Schnorr 디지털서명을 비교하면서 Schnorr 디지털서명이 여러 가지 장점을 통해 블록체인의 미래 디지털서명 대안이 될 가능성이 충분하다고 생각된다. Schnorr는 보안성, 효율성, 가단성, 선형성, 배치검증, 다중서명에 이르기까지 다양한 측면에서 그 성능의 우수성을 알 수 있었다. 특히, 선형성 특성에서는 더 높은 수준의 구축이 가능해 그 활용 가능성이 무궁무진해 보인다.
이러한 Schnorr 디지털 서명의 장점들에도 불구하고 대부분 블록체인 업계에선 표준화가 잘 되어있는 ECDSA 사용을 선호한다. 하지만 향후 몇 년 안으로 대부분의 업체에서 Schnorr 디지털서명이 ECDSA를 대체할 거라 예상된다. 더 나아가, 우리는 제시된 장점들 이외의 Schnorr가 가지는 추가적인 기능과 새로운 혁신을 이해할 수 있는 연구를 계속하려고 한다. 우리는 기술적 측면을 더욱 깊이 파고들어 블록체인에서 Schnorr 디지털서명이 어떤 활용 가능성을 찾을 수 있는지에 대한 연구를 계속할 것이다.
Acknowledgments
이 논문은 2019년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No.2019R1A2C1008533)(2016R1A2B4012386) 또한 “이 논문은 2022학년도 홍익대학교 학술연구진흥비에 의하여 지원되었음”
References
- S. Nakamoto, Bitcoin: A peer-to-peer electronic cash system, 2008 [Internet]. Available: https://bitcoin.org/bitcoin.pdf
- V. Buterin, Ethereum white paper, Ethereum Foundation, 2014[Internet]. Available: https://ethereum.org/en/whitepaper/
- A. M. Antonopoulos and G. Wood, Mastering Ethereum: Building smart contracts and dapps, O’ Reilly Media, Inc.2018.
- Hash Net, Digital Signature [Internet]. Available: http://wiki.hash.kr/index.php/%EB%94%94%EC%A7%80%ED%84%B8%EC%84%9C%EB%AA%85
- H. W. Lee, D. W. Hong, H. I. Kim, C. H. Seo and K. S. Park, “An Implementation of an SHA-3 Hash Function Validation Program and Hash Algorithm on 16bit-UICC,” Journal of KIISE, Vol.41, No.11, pp. 885-891, November 2014
- D. R. L. Brown, SEC 1: Elliptic Curve Cryptography, Standards for Efficient Cryptography, Certicom Research, May 2009. https://www.secg.org/sec1-v2.pdf
- D. R. L. Brown, SEC 2: Recommended Elliptic Curve Domain Parameters, Standards for Efficient Cryptography, Certicom Research, Jan. 2010. https://www.secg.org/sec2-v2.pdf
-
L. Chen, D. Moody, A. Regenscheid, and K. Randall, Recommendations for Discrete Logarithm-Based Cryptography (NIST 800-186 Draft), National Institute of standards and technology (NIST), October 2019.
[https://doi.org/10.6028/NIST.SP.800-186-draft]

- C. Hoskinson, Cardano white paper : Why we are building Cardano, Cardano Foundation, June 2017 [Internet]. Available: https://whitepaper.io/coin/cardano
- L. Ducas, Accelerating BLISS: the geometry of ternary polynomials, Cryptology ePrint Archive: Report 874, October 2014.
- A. Yakovenko, Solana white paper: A new architecture for a high performance blockchain, Solana Foundation, 2018 [Internet]. Available: https://whitepaper.io/coin/solana
- G. Wood, Polkadot white paper: Vision for a heterogeneous multi-chain framework, Polkadot Foundation, 2020 [Internet]. Available: https://whitepaper.io/coin/polkadot
- K. Marszalek and B. Bao, Crypto.com white paper 1.0, Crypto.com Foundation, November 2018 [Internet]. Available: https://whitepaper.io/coin/crypto-com-chain
- J. Sun, Tron white paper, Tron Foundation, 2018 [Internet]. Available: https://whitepaper.io/coin/tron
- Hash Net, Schnorr Signature [Internet]. Available: http://wiki.hash.kr/index.php/%EC%8A%88%EB%85%B8%EB%A5%B4%EC%84%9C%EB%AA%85, .
- J. K. P. Alegro, E. R. Arboleda, M. R. Perena and R. M. Dellosa, “Hybrid Schnorr, RSA, and AES Cryptosystem,” International Journal of Scientific & Technology Research, Vol.8, Issue 10, October 2019.
-
P. S. L. M. Barreto and M. Naehrig, "Pairing-Friendly Elliptic Curves of Prime Order", Selected Areas in Cryptography-SAC 2005. volume 3897 of Lecture Notes in Computer Science, pp. 319-331, August 2005.
[https://doi.org/10.1007/11693383_22]

- G. Soldati, An Advanced Signature Scheme: Schnorr Algorithm and its Benefits to the Bitcoin Ecosystem, Master’s thesis, Politecnico di Milano, Italy, 2018.
- Bc. Antonin Dufka, Schnorr signatures with Application to Bitcoin, Master’s thesis, Masaryk University Faculty of Informatics, Czech Republic, 2020.
- W, Bi, X. Jia and M. Zheng, “A Secure Multiple Elliptic Curves Digital Signature Algorithm for Blockchain,” arXiv preprint arXiv:1808.02988, August 2018.
-
D. R. L. Brown, “Generic Groups, Collision Resistance, and ECDSA,” Springer, Designs, Codes and Cryptography, 35, pp.119-152, April 2005.
[https://doi.org/10.1007/s10623-003-6154-z]

- E. Kiltz, D. Masny, and J. Pan, Schnorr signatures in the Multi-User Setting, Cryptology ePrint Archive: Report 1122, November 2015.
-
M. Bellare and G. Neven, “Multi-Signatures in the Plain PublicKey Model and a General Forking Lemma,” ACM Conference on Computer and Communications Security, pp. 390–399, October 2006.
[https://doi.org/10.1145/1180405.1180453]

-
W. Fang, W. Chen, W. Zhnag, J. Pei, W. Gao and G. Wang, “Digital signature scheme for information non-repudiation in blockchain: a state of the art review,” EURASIP Journal on Wireless Communications and Networking, pp.1-15, March 2020.
[https://doi.org/10.1186/s13638-020-01665-w]

-
G. Maxwell, A. Poelstra, Y. Securin and P. Wuille,. “Simple Schnorr multi-signatures with applications to Bitcoin,” Designs, Codes and Cryptography, 87.9: 2139-2164. February 2019.
[https://doi.org/10.1007/s10623-019-00608-x]

저자소개

2018년 : 전남과학대학교 게임제작과 (전문학사)
2021년 : 홍익대학교 게임학부 게임소프트웨어전공 (학사)
2021년~현 재: 홍익대학교 대학원 게임학과(공학계열) 석사과정
※관심분야 : 게임서버, 블록체인, 이더리움, 디지털서명, NFT 등

2005년 : 고려대학교 대학원 (이학박사-전산학)
2005년~2006년: Wright State University Post-Doc
2007년~현 재: 홍익대학교 게임학부 게임소프트웨어전공 교수
※관심분야 : 게임서버, 로드 밸런싱, 이종블록체인의 상호운용성, 블록체인기반 메타버스 플랫폼 등