반복적 직접 이진 탐색 알고리즘을 이용한 컴퓨터 생성 홀로그래피 기반의 풀 컬러 이미지의 광학적 복원

Ⅰ. 서 론

홀로그래피는 3차원 디스플레이 시스템의 미래 세대를 위한 가장 유망한 기술 중 하나이다. 이것은 시청자에게 모든 시각에 대한 자연스러운 깊이 정보를 제공하여 시각적 피로와 불편함으로부터 벗어나게 해주는 유일한 기술이다. 전통적으로 홀로그램은 기준면과 대상 파면 사이의 간섭을 기록함으로써 생성된다. 그러나 이것은 어두운 방에서 간섭성 광을 갖는 안정된 광학 시스템을 필요로 한다. 이에 대한 대안으로 컴퓨터 생성 홀로그램 (CGH; Computer generated hologram)이 있다 [1]. 그러나 디지털 홀로그래피를 기반으로 한 3차원 디스플레이 시스템을 개발하기 위해 극복해야 할 몇 가지 기술적 과제가 남아 있다 [2]. 이러한 문제점들 중 하나는 디지털 홀로그래피가 간섭성 광 간섭계에 기초하고 있기 때문에 일반적으로 단색 레이저가 기록과 디스플레이 모두에 대한 광원으로서 사용된다는 사실로부터 발생한다. 컬러 홀로그램 디스플레이의 경우 빨강, 녹색 및 파랑 (RGB) 구성 요소 각각을 복원하는 데 3개의 다른 레이저를 사용해야 한다. 파장에 따라 회절 각이 다르므로 서로 다른 레이저로 조명된 동일한 홀로그램이 동일한 대상을 복원 할 수는 있지만, 파장에 따라 크기와 초점에 차이가 발생한다. 이러한 오류는 R, G 및 B 홀로그램 크기와 초점 평면을 조정하여 수치로 보정 할 수 있다 [3]. 또한 색수차와는 상관없이 광학 복원 시 디스플레이 장치로 사용되는 공간 광 변조기 (SLM; spatial light modulator)가 진폭 및 위상 변조를 동시에 처리 할 수 ​​없기 때문에 복소 디지털 홀로그램을 직접 디스플레이하는 것은 불가능 하다. 몇 가지 솔루션이 제안되었지만 [4, 5], 가장 적합한 방법은 복소 홀로그래픽 데이터를 이진 바이너리 포맷으로 변환하는 것이다.

본 논문에서는 컴퓨터 생성 홀로그램으로 기록한 풀 컬러 이미지 홀로그램을 광학적으로 복원 할 수 있는 방법을 제안한다. 우수한 품질의 복원 결과를 보장하는 것으로 알려진 직접 이진 검색 (DBS; direct binary search) 알고리즘을 사용하여 풀 컬러 복소 홀로그램 데이터를 이진 바이너리 홀로그램 데이터로 변환하고, 파장에 의해 발생하는 색수차는 이진 홀로그램의 복원 파라미터를 조정함으로써 수치적으로 수정하여 해결하였다.

Ⅱ. 컴퓨터 생성 홀로그램

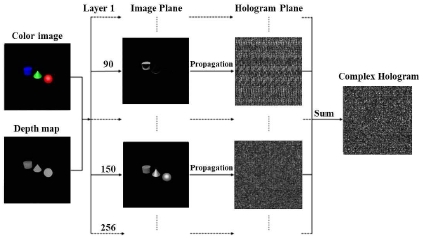
컴퓨터 기술의 발전으로 오늘날 3차원 객체의 가상 모델을 만들 수 있다. 컴퓨터 생성 홀로그램은 가상의 3차원 모델에 해당하는 홀로그래픽 간섭 패턴을 인위적으로 만드는 기술로, 포인트 클라우드 (point cloud) 또는 폴리곤 메쉬 (polygon mesh) 를 이용하는 방법과 깊이 맵 (depth map) 을 이용하는 방법이 있다. 포인트 클라우드나 폴리곤 메쉬를 이용하는 방법은 가상 모델의 모든 요소에 대한 기여가 홀로그램 평면의 모든 지점에서 계산되어야 한다는 단점이 있다. 따라서 가상 객체를 정확하게 나타내기 위해서는 수천 개의 점을 사용해야하기 때문에 엄청난 연산 능력이 필요하다. 반면에, 한 평면에서 다른 평면으로의 확산은 프레넬 (Fresnel) 또는 콘벌루션 (convolution) 공식을 사용하면 쉽게 구현 할 수 있다. 홀로그램 면과 평행한 다수의 2차원 평면으로 3차원 물체를 표현하는 것이 제안되었다 [6,7]. 생성한 3차원 객체를 2차원 슬라이스로 표현한다면 컴퓨터 생성 홀로그램은 각 슬라이스의 홀로그램 평면으로의 확산을 계산하여 생성할 수 있다.

3차원 객체로부터 복소 홀로그램을 얻기 위해서는 객체의 컬러 영상과 깊이맵 영상을 이용해야 한다. 먼저 객체의 컬러 영상을 R, G, B로 각각 분리하여 영상의 2차원 정보와 광 세기 정보를 얻고, 깊이 맵은 256개로 나눠서 표현한다. 각 층의 깊이는 0부터 255 사이의 선형 방식으로 설정되어 Z축의 깊이 값으로 사용된다. 깊이 범위는 값 0과 255에 해당하는 층의 실제 깊이 값 (mm)을 설정하여 정의 할 수 있다. 깊이맵을 이용한 컴퓨터 생성 홀로그램 계산의 원리는 그림 1에 나타내었다. 이와 같은 방식으로 컬러 영상와 깊이맵으로 부터 얻은 3차원의 정보를 이용하여 복소 홀로그램을 생성할 수 있다. 우리는 RGB에 해당하는 3차원 오브젝트 도형을 만들어 그림 1의 절차를 통해 복소 홀로그램 데이터를 획득하였다.

Fig. 1.

Principle of computer generated hologram.

Ⅲ. 이진 홀로그램을 이용한 광학 복원

2-1 DBS(direct binary search) 알고리즘

컴퓨터 생성 홀로그램 방법을 통해 복소 홀로그램 데이터를 얻었지만, 복소 홀로그램 데이터는 SLM에 직접로드 할 수 없기 때문에, 데이터 형식은 광학 복원을 위한 디스플레이 장치에 적합한 형태로 변환해야 한다. 대부분의 SLM은 진폭과 위상 중 한 가지만 변조하도록 설계된 것이기 때문에, 두 가지를 동시에 변조하지는 않는다. 따라서 홀로그램 데이터를 디스플레이 시스템에서 사용되는 SLM에 적합한 데이터 포맷인 이진 바이너리 데이터로 변환하는 것은 필수적이다. 바이너리 홀로그램을 생성하기 위한 몇 가지 방법이 제안되었는데, 가장 기본적인 방법은 복소 홀로그램 데이터에 간단한 임계값을 적용하는 것이다. 픽셀 값의 실수 부분은 양수 1로, 그렇지 않으면 0으로 설정하는 방식이다. 구현이 어렵지 않고 단 시간 내에 결과를 얻을 수 있지만 광학 복원 시 품질이 좋지 않다는 단점이 있다. 이에 화질 개선을 위한 방법으로 양방향 오차 확산 (BERD; bidirectional error diffusion)을 기반으로 한 방법도 보고되었지만, 이 두 가지 방법은 비 반복적인 방법으로 연산속도가 빠르다는 장점이 있지만, 복원 시에 복원 평면에서 일정 수준의 화질 열화가 일어나는 것을 피할 수는 없다 [8]. 반면에 DBS 알고리즘은 반복적인 방법이기 때문에 연산 속도는 느리지만, 고품질의 복원 이미지를 얻을 수 있다는 것이 입증되었다. DBS 알고리즘 흐름도는 그림 2에 나타내었다.

Fig. 2.

The DBS-algorithm flowchart.

먼저 랜덤 바이너리 패턴을 생성하여 하나의 픽셀을 0 또는 1의 값으로 설정하고, 설정한 복원 거리에 대한 복원 평면을 생성한다. 생성된 복원 평면은 수식 (1)에 보인 평균 제곱 오차 (MSE; mean square error) 분석을 통해 복소 홀로그램에 의해 생성된 기준 평면과 비교한다.

$\[ \begin{array}{c}MSE=\frac{1}{M•N}\frac{\sum _{m=\frac{-M}{2}}^{\frac{M}{2}-1}\sum _{n=\frac{-N}{2}}^{\frac{N}{2}-1}I{m}_{ref}\left(m,n\right)-k•{Im}_{bin}\left(m,n\right)}{\sum _{m=\frac{-M}{2}}^{\frac{M}{2}-1}\sum _{n=\frac{-N}{2}}^{\frac{N}{2}-1}\left|I{m}_{ref}{\left(m,n\right)}^2\right|}\\ with k=\frac{\sum _{m=\frac{-M}{2}}^{\frac{M}{2}-1}\sum _{n=\frac{-N}{2}}^{\frac{N}{2}-1}I{m}_{bin}\left(m,n\right)-conj\left|{Im}_{bin}\left(m,n\right)\right|}{\sum _{m=\frac{-M}{2}}^{\frac{M}{2}-1}\sum _{n=\frac{-N}{2}}^{\frac{N}{2}-1}\left|I{m}_{bin}{\left(m,n\right)}^2\right|}\end{array} \]$

(1)

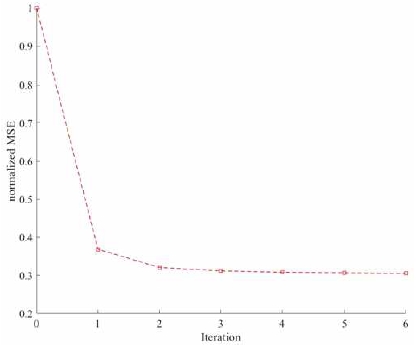
여기서 M과 N은 홀로그램의 행과 열의 개수, conj[.]는 공액 연산자이고, Im_ref와 Im_bin은 복소 행렬이다. 수식 (1)을 통해 계산된 MSE 값이 개선 된 경우 픽셀 값이 유지되고, 그렇지 않으면 이전 값으로 반환한다. 모든 픽셀은 1 대 1 방식으로 계산하고 연산이 끝나면 첫 번째 픽셀로 돌아가 절차를 반복한다. 계산 시간을 줄이기 위해 복원 평면 내에 객체가 있는 부분을 관심 영역 (ROI; region of interest)으로 지정하여 그 영역에서만 MSE를 계산한다. 앞서 언급했듯이 DBS 알고리즘은 절차를 반복할 수 있기 때문에, 반복 횟수에 따라 화질을 향상시킬수 있다. 그림 3은 반복 횟수에 따른 정규화된 MSE의 변화를 나타낸 것이다. 1회 반복과 2회 반복의 차이는 크지만 2회 이상부터는 거의 동일한 것을 볼 수 있다. 계산 시간과 화질 향상 정도를 봤을 때, 두 번의 반복 작업만으로도 고품질의 바이너리 홀로그램을 얻을 수 있다.

Fig. 3.

Evolution of normalized MSE as a function of iteration number.

2-2 광학 복원을 위한 색수차 보정

DBS 알고리즘에 의해 생성된 이진 바이너리 홀로그램을 광학적으로 복원하기 위해, 우리는 7.0μm의 픽셀 피치와 1366 × 768 픽셀의 해상도를 갖는 LCoS 공간 광 변조기 (SLM, Cremotech, C200)를 사용하였다. 이진 바이너리 홀로그램 데이터의 픽셀 크기를 SLM의 해상도와 일치시키기 위해 제로 패딩을 사용하였다. 광학 복원 시에 RGB 각 색의 색수차 때문에 색상 별로 복원된 이미지의 초점과 크기가 달라지는데, RGB 이미지를 결합하여 풀컬러 영상으로 보기 위해서는 DBS 알고리즘으로 이진 홀로그램을 생성 할 때 복원 파라미터를 계산하여 색상 별로 각각 적용해야 한다. 복원 거리, 파장 및 이미지 크기 사이의 관계는 아래 브래그 방정식 (Bragg’s law)에 의해 주어진다 :

$\[ z=\frac{N\times p_{im}\times p_{holo}}{\lambda } \]$

(2)

여기서 z는 복원 거리, N은 픽셀 번호, p_im은 홀로그램 픽셀 피치, p_holo는 이미지 평면, λ는 파장이다. 식 (3)에 따르면, 복원 거리와 이미지 크기는 파장에 의존한다. 색수차에 의한 크기 오차를 보상하기 위해서는, 2진 홀로그램 패턴의 픽셀 수 N을 아래 수식 (3)이 되도록 조정해야한다.

$\[ \frac{N_R}{{\lambda }_R}=\frac{N_G}{{\lambda }_G}=\frac{N_B}{{\lambda }_B}. \]$

(3)

홀로그램 패턴의 픽셀수를 조정함으로써 모든 파장에 대해 픽셀 피치를 동일하게 조절하면, 획득한 RGB 이미지를 결합하여 한 장의 풀컬러 이미지를 만들 수 있다. 그림 4 (a) - (c)는 색수차를 보정하여 동일한 초점 거리에서 복원된 R, G, B 결과를 보여 주며, (d)는 (a), (b) 및 (c)를 결합한 이미지이다. 복원한 객체를 동일한 위치에 설치한 상보성 금속 산화막 반도체 (CMOS; complementary metal-oxide-semiconductor) 카메라 (Imaging Source, DFK 23GP031)로 촬영하였다.

Fig. 4.

Optical reconstruction of the RGB components of a hologram with a binary pattern. (a) Red, (b) green (c), blue, and (d) combined image;

색수차 보정을 통해 R, G 와 B의 초점거리가 동일하게 조정되어 결합한 풀 컬러 이미지를 그림 4 (d)에서 확인할 수 있다. 그림 4 (a)의 R은 다른 색에 비해 잡음이 덜하고 크기가 약간 크다. 반대로 그림 4 (c) B의 경우 다른 색에 비해 선명하지만 잡음이 많다. 적색의 파장이 길고, 청색 파장이 짧은 파장의 특성 때문이다.

Ⅳ. 결 론

우리는 컴퓨터 생성 홀로그램으로 얻은 풀 컬러 홀로그래픽 데이터를 광학적으로 복원하는데 성공하였다. 복소 홀로그래픽 데이터를 광학적으로 복원 할 수 있는 형태인 바이너리 홀로그램 데이터로 변환하는 데 DBS 알고리즘을 사용하였다. 반복적인 특성 때문에 DBS 알고리즘이 비 반복적인 방법보다 속도는 느리지만 우수한 이미지 품질을 보장함으로써 풀 컬러 광학 복원에 적합하다는 것을 결합된 이미지를 통해 보여 주었다. 광학 복원 시에 각 색의 파장에 의해 야기된 색수차는 이진 홀로그램의 복원 파라미터를 수정함으로써 보정하였다. 우리가 알고 있는 한, 이것은 컴퓨터 생성 홀로그래픽으로 기록된 풀 컬러 홀로그램의 광학 복원을 한 것은 최초이다.

Acknowledgments

본 연구는 문화체육관광부 및 한국콘텐츠진흥원의 2018년도 문화기술연구개발 지원사업(R2018020085)으로 수행되었음.

References

• Chen, R. H. Y., and Wilkinson, T. D., “Computer generated hologram from point cloud using graphics processor”, Applied Optics, 48(36), p6841-6850, (2009).
• Jia, J., Liu, J., Wang, Y. T., Pan, Y. J., and Li, X., “Study on basic problems in real-time 3D holographic display”, in Proceeding of the SPIE, 8738, p87380F, (2013).
• Yu, Y. J., Wang, T., Dai, L. M., Zheng, H. D., and Asundi, A., “Method for compensation of transverse dispersion in electro-holography”, in Proceeding of the SPIE, 7522, p752220, (2010).
• Leportier, T., Park, M. C., and Kim, T, “Numerical alignment of spatial light modulators for complex modulation in holographic displays”, Journal of Display Technology, 12(10), p1000-1007, (2016). [https://doi.org/10.1109/jdt.2016.2576446]
• Reichelt, S., Haussler, R., Futterer, G, Leister, N, Kato, H, Usukura, N., and Kanbayashi, Y, “Full-range, complex spatial light modulator for real-time holography”, Optics Letter, 37(11), p1955-1957, (2012). [https://doi.org/10.1364/ol.37.001955]
• Chen, J-S., and D. P. Chu, "Improved layer-based method for rapid hologram generation and real-time interactive holographic display applications", Optics express, 23(14), (2015), p18143-18155.
• Chen, Jhen-Si, Daping Chu, and Quinn Y. Smithwick, "Rapid hologram generation utilizing layer-based approach and graphic rendering for realistic three-dimensional image reconstruction by angular tiling", Journal of Electronic Imaging, 23(2), (2014), p023016.
• Tsang, Peter Wai Ming, and T-C. Poon, "Novel method for converting digital Fresnel hologram to phase-only hologram based on bidirectional error diffusion", Optics express, 21(20), (2013), p23680-23686.