Sentence Comprehension with an LSTM Language Model
Copyright ⓒ 2018 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract
We are to build a Long Short-Term Memory (LSTM) network-based language model which can estimate the amount of information that words in sentences convey. We are then to investigate whether reading-times on words in a sentence are predicted by information-theoretic measures such as surprisal and entropy reduction. Specifically, the proposed LSTM deep-learning model is first to be trained on the large dataset of learner English sentences and is then to be applied to estimate the two different information-theoretic measures on each word of the test data of English sentences. The reading times on the words in the test data are to be collected from the Korean English L2 learners reading the test sentences. A comparison between the information-theoretic measures and reading-times by using a linear mixed effect model reveals a reliable relationship between surprisal/entropy reduction and reading time. We conclude that both surprisal and entropy reduction are positively related to the processing effort (i.e. reading time), confirming the surprisal/entropy-reduction hypothesis.
초록
본 논문에서는 문장에서 단어가 전달하는 정보의 양을 추측할 수 있는 LSTM 신경망 기반 언어 모델링 시스템을 제안하였다. 제안한 시스템을 이용하여 문장의 각 단어에 대한 읽기 시간이 써프라이절과 엔트로피 감소와 같은 정보 이론적 측정치에 의해 예측될 수 있는지 비교 분석하였다. LSTM 기반 언어 모델은 영어 문장 말뭉치를 대상으로 심층 학습이 진행되었으며, 심층 학습된 모델을 통해 실험실에서 한국인 영어 학습자가 읽은 영어 테스트 문장의 각 단어에 대한 써프라이절과 엔트로피 감소 측정치를 계산하였다. 그리고 언어 모델의 문장 처리 결과는 선형 mixed-effect 통계 모델을 구축하여 정보 이론적 측정치와 읽기 시간을 비교 분석하였다. 실험 결과, LSTM 신경망 기반 언어 모델을 이용하여 예측한 문장에 대한 써프라이절과 엔트로피 감소 정보는 문장 이해 (즉, 읽기 시간)와 양의 상관관계가 있음을 써프라이절과 엔트로피 감소 가설을 검증하여 확인할 수 있었다.
Keywords:
Entropy reduction, Long Short-Term Memory network, Language model, Surprisal키워드:
장단기 기억 신경망, 언어 모델, 써프라이절, 엔트로피 감소Ⅰ. INTRODUCTION
In the last several years, there has been substantial success in applying recurrent neural networks (RNNs) to a language modeling. For example, given that a language model tries to predict the next word based on the previous ones in a sentence, if one is trying to predict the last word in “the clouds are in the sky,” one doesn’t need any further context – it’s pretty obvious that the next word is going to be sky. In similar cases, where the gap between the relevant information and the place where it’s needed is small, RNNs can learn to effectively use the information that has evolved.
But there are cases where we need more contextual information in making a prediction. If one is trying to predict the last word in the following discourse like “I grew up in Korea. ⋯ I speak fluent Korean”, the information given immediately prior to the last word (i.e., speak) suggests that the last word at hand is most probably the name of a language, but if we want to narrow down which language it is, we need to retrieve the information from the word Korea given in the preceding sentence further back. It’s thus certainly evident that the gap between the relevant information and the point where it is needed becomes very large.
Unfortunately, as such a gap grows large, RNNs become unable to learn to connect that gap. But the Long Short-Term Memory (LSTM) networks as a special kind of RNN are capable of learning long-term dependencies. LSTMs are explicitly designed to resolve the long-term dependency problem [1].
Much recent works in computational linguistics and natural language processing (NLP) have employed the information theory to bridge between language models and cognitive experiments [2-5]. For example, as one reads a certain sentence, one understands each word based on one’s understanding of previous words. Each word conveys a certain amount of information. The amount of information conveyed by a word (or word-information for short) can be computed from probabilistic models of language, whereas the amount of cognitive effort involved in processing a word can also be calculated by measuring word reading times taken during the task of reading words in a sentence [6-7].
In other words, the reading time for a word in a sentence depends on the amount of information that the word at hand conveys. The relation between the reading time and the measure of word-information has been elaborated on and more clearly defined by the development of sentence-processing models. Particularly, the comparison between reading times and word-information values has revealed that more informative words take longer to read [8].
More relevant to the issue in this paper, several previous studies have shown that surprisal (the next-word entropy effect) and entropy reduction can serve as the cognitively relevant measure for two distinct kinds of word-information process. One recent RNN language model shows that the reading-time effects of both surprisal and entropy reduction can result from a single processing mechanism [9]. It shows that word-processing times in the sentence comprehension model correlate positively with both surprisal and entropy reduction. The model thereby plays an integral role in making a computation-level prediction of the relation between reading times and the two measures of word-information.
Given this background, in this paper we propose a sentence comprehension language model based on a deep-learning LSTM model and investigate whether reading times are predicted by the two kinds of information measure. In section 2, we preview related works on deep-learning language modeling and word-information measures. In section 3, we design a word-predicting language model based on LSTM networks with word embeddings and then describe the corpus and the experimental methods to be employed here. Interpretation of the results is discussed in section 4. Finally, section 5 concludes the discussion.
Ⅱ. METHODS
In this section, we describe the word-information measures, the linear mixed-effects model, and the deep-learning LSTM model of the experimental environment to be built for the language model system implementation of sentence comprehension.
2-1 Word-information measures
The comprehension process for a k-word sentence can be assumed to comprise a sequence of comprehension events for k words: w1, w2, ⋯ , wk or wk1, or w1...k for short. After the first t words of the sentence (i.e., wk1) have been processed, the identity of the upcoming word, wt+1, is still unknown and can be viewed as a random variable.
The first important concept from the word-information theory is surprisal [8]. It is a measure of the uncertainty about the outcome of a random variable, which is quantified by the probability of the actual next word wt+1, given the sentence:
| surprisal(wt+1)=-logeP(wt+1|wt1) | (1) |
Informally, the surprisal of a word can be said to measure the extent to which its occurrence is unexpected.
The language model’s output after processing the sequence wk1 forms an estimate of P(wt+1|wt1) for each possible next word wt+1, which translates directly into the surprisal of the actual upcoming word.
The second important concept from the word-information theory is entropy [8]. After processing the sequence wt1, the uncertainty about the remainder of the sentence is quantified by the entropy of the distribution of probabilities over the possible continuations wt+1 ... k (with k>t). The entropy will be formally defined as
| H(Wt+1…k)=-∑wt+1…kP(wt+1…k|wt1)logP(wt+1…k|wt1) | (2) |
where Wt+1 ... k is a random variable with the particular sentence continuations wt+1 ... k as its possible outcomes.
When the next word is encountered, this will usually decrease the uncertainty about the rest of the sentence, that is, H(Wt+2 ... k) is generally smaller than H(Wt+1 ... k). The difference between the two is the entropy reduction, which will be formally defined
| ∆ | (3) |
Informally, entropy reduction can be said to quantify how much ambiguity is resolved by the current word, to the extent that disambiguation reduces the number of possible sentence continuations.
Entropy is computed over probabilities of the sentences themselves. That is, the Eq. (2) contains only word sequences instead of structures. As a consequence, there is no more uncertainty about what has occurred up to the current word wt. Although the intended structure of may be uncertain, the word sequence itself is not. This means that only the upcoming input sequence (i.e., from wt+1 onward) is relevant for entropy.
However, the number of upcoming input sequences is far too large for the exact computation of entropy, even if infinite-length sequences are not allowed and some upper bound on sequences length is assumed. Therefore, probabilities are not estimated over complete sentence continuations. Instead, the look-ahead distance is restricted to some small value n, that is, only the upcoming n words are considered.
In this paper, we consider that entropy is computed over the distribution , which is computed from the LSTM language model’s output by applying the chain rule:
The definition of entropy from Eq. (2) now becomes
The number of elements in the set Wt+1 ... t+n grows exponentially as the n increases. Consequently, the computation time grows exponentially. In this paper, the current simulations do for n = 3 and 4.
An alternative expression for entropy reduction from Eq. (3) can be simplified as
| (4) |
2-2 Linear mixed-effects model
To model a linear relationship for data points with inputs of word-information measures, we employ a linear mixed-effects model. This model describes the relationship between a response variable and independent variables, with coefficients that can vary with respect to one or more variables. It consists of two parts: fixed effects and random effects. Fixed-effects terms are usually the conventional linear regression part, whereas the random effects are associated with individual experimental units drawn at random from a population.
We fitted a linear mixed-effects model by using the popular lme4 package [10]. The independent variables are word-information values, while the response variable is reading-time values for words in sentences.
2-3 Deep-learning language model
With preprocessed sentences, the words extracted were encoded into dense word embedding.
In NLP, word embedding is a method of mapping that allows words with similar meanings to have similar representations. We used the Word2vec algorithm, which compresses the dimensions of a word vector from the vocabulary size to the embedding dimension [11-12]. To implement the Word2vec algorithm, we trained it with a total 231005 sentences, with 2,760,125 raw words and 8000 unique words, and with a learning rate of 0.025 decreasing by 0.02, decreasing over 10 epochs.
RNN is a neural network that attempts to model time or sequence dependent behaviour like language.
RNN is performed by feeding back the output of a neural network layer at time to the input of the same network layer at time t+1. The problem with vanilla RNN is that as we try to model dependencies between words or sequence values that are separated by a significant number of other words, we experience the vanishing gradient problem. This is because small gradients or weights (values less than 1) are multiplied many times over through the multiple time steps, and the gradients shrink asymptotically to zero. This means that the weights of those earlier layers won’t be changed significantly, and therefore the network won’t learn long-term dependencies.
LSTMs are a way of solving this problem for word prediction. An LSTM network has LSTM cell blocks in place of our standard neural network layers. These cells have various components called the input gate (which acts to “kill off” any elements of the input vector that are not required), the forget gate (which helps the network learn which state variables should be “remembered” or “forgotten”), and the output gate (which determines which values are actually allowed as an output from the state cell).
In LSTMs, all the weights and bias values are matrices and vectors, respectively. Input data are represented as Word2vec embedding vector to input words to a neural network, which involves taking a word and finding a vector representation of that word which captures some meaning of the word.
In the section 3.1 to follow, we set up what is called an embedding layer, to convert each word into a meaningful word vector. We have to specify the size of the embedding layer (which the length of the vector each word is represented by). This is usually in the region of between 100-500. In other words, if the embedding layer size is 400, each word will be represented by a 400-length vector( i.e., [x1, x2, ⋯, x399, x400])
Ⅲ. PROPOSED LANGUAGE MODEL
A language model can predict the probability of the next word in the sequence, based on the words already observed in the sequence. Neural network models are a preferred method for developing statistical language models because they can use a distributed representation where words with similar meanings have similar representations and because they can use a large context of recently observed words when making predictions .
We build a language model to predict the word-to-word of a sentence by using LSTM networks.
3-1 LSTM language model architecture
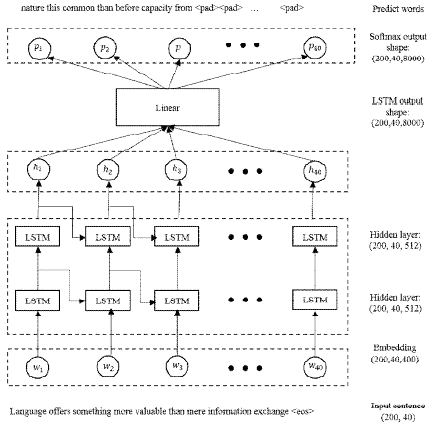
This section illustrates what a full LSTM language model architecture looks like. Fig. 1 presents a word-to-word prediction model including multiple layers such as input layer, embedding layer, two LSTM layers, linear layer, Softmax layers, and output layer.
The input sentence (for example, Language offers something more valuable than mere information exchange <eos>) with an extra unit that represents <eos>; that is, the end of the sentence is fed into the embedding layer and then two layers of LSTM cells. We define the shape of the inputs as batch size and maximum-length of a sentence. In the diagram the LSTM network is shown as unrolled over all the time steps. Each input unit corresponds to one word, making maximum input units (i.e., 40 words) fix maximum-length words in the input sentence with variable length.
Specially, for each input unit in the number of time steps, we set a 400 length word embedding vector to represent the input word. These embedding vectors are pre-trained before the overall model learning.
The LSTM layer’s output units represent predictions of subsequent inputs. We set the hidden-state size as 512. So, the output units has (batch size, maximum-length sequence, hidden-state size) dimensional shape. The output units from hidden LSTM layers are applied to a linear layer of size (batch size, hidden-state size, vocabulary size). Then the outputs from the linear layer at each time step are passed to a Softmax layer with a Softmax activation. The Softmax function makes sure that the output unit sums to one and can therefore be viewed as a probability distribution.
The output layer also has one unit for each predicted word, plus an extra unit that represents padding character <pad>, that is, the correction of the maximum length of the sentence (for example, nature this common than before capacity from <pad> <pad> ...<pad>). The output unit is compared with the training data, and the error and gradient back propagation is performed from there. The training data in this case is the input words advanced one time step. In other words, at each time step the model is trying to predict the very next word in the sequence.
3-2 Data
We trained a language model of English, based on a dataset which contains a collection of all the 231005 sentences (a total of 2,760,125 word tokens, and 30,606 unique words) from the written-text. The dataset was compiled from a collection of middle and high school English textbooks published in Korea in 2001 and 2009.
Meanwhile, the test sentences to measure word reading times were collected from the College Scholastic Ability Tests administered in Korean in 2016 and 2017. They consist of 58 sentences and contain 1,047 words. The average sentence length is 18.1 words, with a maximum of 37. One example sentence from these experimental sentences is shown in Table 1.
In the reading time experiment, each test sentence preceded by a fixation cross was presented in a word-by-word manner, with each word in 23-point Courier New font appearing at the center of the screen. The stimuli were presented in a self-paced reading paradigm controlled by E-prime psychology tool. The sentences were followed by a yes/no comprehension question.
Thirty (male: 20) Korean L2 late learners of English (mean age: 24 years, SD: 1.7) without immersion education in the L2 English environment before puberty participated in the present experiment. All the participants were undergraduate students, and their English proficiency was relatively high; they had high scores on TOEIC (mean: 932.6, SD: 45.1, range: 850-990). They gave written informed consent to their participation and were paid for their participation.
For pre-processing, sentence initial and sentence-final words were removed, as well as words directly following a comma. We then log-transformed reading times and standardized word-length, sentence position, and word position for a linear mixed-effects regression model [13-14].
3-3 A sentence comprehension with language model
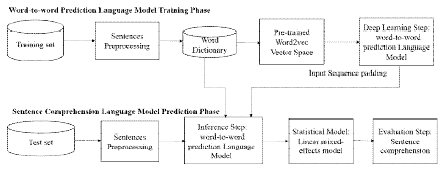
This section introduces the process of a sentence comprehension with our language modeling system. As depicted in Fig. 2, in the training phase the text preprocessing steps are built with certain NLP tools so as to better ensure the accuracy of our output. Then the texts are represented in a pre-trained Word2vec vector space and used as input for the LSTM model in Fig. 1. We train a language model over the training set.
In the prediction phase, we build the prediction model to predict the next word using the trained model. The model predicts the probability of each word, given a history of previous words in the input sentence. The predicted words are fed in as input to in turn generate the next word.
Finally, we build a linear mixed-effect model to evaluate the sentence comprehension with the word-to-word prediction by using the two measures of surprisal and entropy reduction and compare the correlation between the two word-information measures and the reading time.
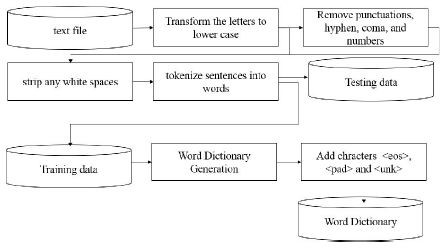
In order to get the sentence into the right shape for input into the LSTM language model, each unique word in the text file must be assigned a unique integer index.
As depicted in Fig. 3, the unstructured sentence is first pre-processed in the following three steps: The first step is to transform the letters to lower case, remove punctuations, hyphen, coma, and numbers from the text, and strip any excess white spaces from them. The second step is to tokenize sentences into words. The last step is to save training words and test words into two separate files for usage in the training and test steps.
Basically, the given text file (including sentences with <eos>) was preprocessed into separate words and <unk>. In other words, only the most frequent words (8000 words) were stored in its word dictionary, the others were replaced by the token <unk>, and the words were separated with spaces according to consistent tokenization rules, and the sentences were segmented one per line.
Finally, the original text file was converted into a list of these unique integers, where each word is substituted with its new integer identifier. This allows sentences to be consumed in the neural network.
As in Fig. 2, we convert our words (referenced by integers in the data) into meaningful embedding vectors using the vocabulary dictionary and pre-trained Word2vec model.
The input sequences in the input layer need to be long enough to allow the model to learn the context for the words to predict. To pad input sequences to the same length, we tested the ability of the model to learn with differently sized input sentence. So we built a matrix of (batch size, input size, vocabulary size) where each row corresponds to a word embedding vector and the length of the input sentence is 40 words.
Input sequences that are shorter than 40 words are padded with value (i.e., <pad>) at the end. The longer input sequences are truncated so that they fit the desired length. This layer replaces each word index with a word vector of size (200, 40, 8000).
The model we trained learns to predict the probability distribution for the next word using the context of the preceding words. It predicts the next word with a probability for each word in the vocabulary.
We here specify the type of optimization to perform the given model. The LSTM model is compiled specifying the categorical cross entropy loss needed to optimize the model. For this purpose the efficient Adam optimizer was used.
In order to get good results, we have to run the model over many epochs, and the model needs to have a significant level of complexity to optimize learning parameters. Therefore, we run the model up to 10 epochs and get some reasonable initial results.
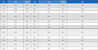
Finally, the model was optimized on the training data for 5 training epochs with optimal model parameters. The results are as follows in Table 2 and 3: batch size=200, input size=40, hidden size=512, vocabulary size=8000. After 5 epochs, training accuracy was around 82%, while validation accuracy reached approximately 81%.
As depicted in Fig.2, the next word from the previous word given test sentences is predicted in the following two steps. The first step is to preprocess sentences. The second step is to predict the upcoming word in a sentence using the optimal LSTM model and compare the predicted word outputs with the actual word sequences from the test set.
The optimal LSTM model was employed to get the three different word-information values such as surprisal and two entropy-reductions from Eq. (1) and Eq. (4) on each word of a test set of English sentences.
To estimate the sentence processing with the word-to-word prediction using the two measures of surprisal and entropy reduction, we formulated a linear mixed-effect model in the lmer package for R language as follows:
| (5) |
where the term (1|Object) means the random effect variable. The term log(RT) means the log function value of reading-time values for words. Model represents a linear mixed-effects model using the lmer function with one dependent variable log(RT) and fixed effect three variables from Eq. (1) and Eq. (4).
3-4 Experimental environment
In this section, we describe the hardware and software of the experimental environment built for the implementation of proposed system.
Table 4 shows the hardware used in the experiment: NVIDIA GTX 1080 is used as the graphics processing unit (GPU) specification to shorten learning time. The central processing unit (CPU) is i5-2500K, and memory is 32G. The hard disk drive (HDD) uses 256G SSD.
Table 5 shows the software used in the Windows 7 experiment: We used PyCharm, a python development toolkit, for python-based projects. We preprocessed the sentences by using the natural language toolkit (NLTK) library which is a Natural Language Toolkit. The Word2Vec module uses Gensim open source. The proposed LSTM language model was implemented using Tensorflow and Keras open source. We measured the reading time of the sentences using E-Prime psychology tool and implemented the liner mixd-effects model by using lme4 package.
Ⅳ. THE RESULT: LANGUAGE MODEL, READING-TIME, & THEIR CORRELATION
4-1 Word-information extraction from sentences
The language model was used to compute surprisal and entropy reduction values for each word of the test sentences.
Table 6 shows an example of 16-word sentence, with each word’s surprisal and ΔH3 and ΔH4 being estimated by the model. It shows that the values of entropy reduction from ΔH3 to ΔH4 correspond to a decrease in entropy. The reading times on the words in the same sentence were collected from the Korean English L2 learners reading the test sentences.
4-2 Relationship between information measures
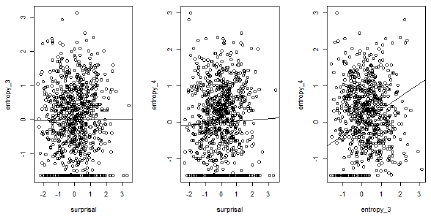
In Table 6, surprisal and two kinds of entropy reduction ΔH3 and ΔH4 are taken as measures for the amount of information conveyed by words. We assume the entropy-reduction hypothesis that information-theoretic measures are positively correlated with the reading-time cognitive measures.
Fig. 4 shows the linear relationship between three measures with surprisal, ΔH3, and ΔH4. However, it shows that the correlation between surprisal and entropy reduction is in fact quite weak. This means that surprisal and entropy reduction come into play independently during sentence processing. In contrast, the two measures of entropy reduction ΔH3 and ΔH4 correlate very strongly with each other.
To check the correlation between word-information measures and cognitive measure (i.e., reading time), we performed the linear mixed-effects regression model from Eq. (5). Using the statistical hypothesis test with the std. error (which is the standard deviation of the sampling distribution of a statistic, most commonly of the mean) and the t value and Pr-value, we observe in Table 7 that both surprisal and entropy reduction ΔH4 have statistically significant p-values. However, we note in Table 7 that ΔH3 does not have a statistically significant p-value.
Ⅴ. CONCLUSION
The proposed system has shown that the reading-time effect of both surprisal and entropy reduction can indeed result from a sentence processing/comprehension with a single recurrent neural network model. It has simulated sentence comprehension by employing the Word2vec representation described by a sentence. In this network model, surprisal and entropy reduction have been defined by a probabilistic LSTM model rather than the traditional language model. The amount of cognitive effort required to process a word has been argued to depend on the uncertainty of that word in an evolving sentence, as quantified by the entropy over sentence probabilities.
We have tested this hypothesis more thoroughly than has been done before by using an LSTM network for the estimation of surprisal and entropy reduction. A comparison between these estimates and word-reading time shows that entropy reduction ΔH4 is positively related to the word reading or processing cognitive effort, confirming the entropy-reduction hypothesis. The effect of surprisal is also correlated with the word reading or processing cognitive effort.
Acknowledgments
This work was supported the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF - 2017S1A5A2A01026286).
References
- S. Hochreiter, and J. Schmidhuber, “Long short-term memory”, Neural computation, p1735-1780, (1997).
- D. Kleinschmidt, R. Raizada, and T. Jaegar, “Supervised and unsupervised learning in phonetic adaption”, Proc. Of the 37th annual conference of the cognitive science society, CA, p1129-1135, Jul.), (2015.
- T. Young, D. Hazarika, S. Poria, and E. Cambria, “Recent Trends in Deep Learning Based Natural language Processing”, arXiv:1708.02709, Oct.), (2018.
-
M. F. Boston, J. Hale, S. Vasishth, and R. Kliegl, “Parallel processing and sentence comprehension difficulty”, Language and Cognitive processes, 26, p301-349, Jan.), (2011.
[https://doi.org/10.1080/01690965.2010.492228]

-
Y. Liu, and M. Zhang, “Neural Network Methods for Natural Language Processing”, Computational Linguistics, 44, p193-195, Mar.), (2018.
[https://doi.org/10.1162/coli_r_00312]

- J. Hale, “Uncertainty about the rest of the sentence”, Cognitive Science, 30, p643-672, Feb.), (2010.
-
N. J. Smith, and R. Levy, “The effect of word predictability on reading time is logarithmic”, Cognition, 128(3), p302-319, Jun.), (2013.
[https://doi.org/10.1016/j.cognition.2013.02.013]

- J. Hale, “The information conveyed by words in sentences”, Journal of Psycholinguistic Research, 32, p101-123, Mar.), (2003.
-
S. L. Frank, L. J. Otten, G. Galli, and G. Vigliocco, “The ERP response to the amount of information conveyed bywords in sentences”, Brain & Language, 140, p1-11, Jan.), (2015.
[https://doi.org/10.1016/j.bandl.2014.10.006]

- D. Bates, M. Machler, B. Bolker, and S. Walker, “Fitting Linear Mixed-Effects Models Using lme4”, Journal of Statistical Software, 67, p1-48, Oct.), (2015.
- T. Mikolov, K. Chen, G. Corrado, and J. Dean, “Efficient estimation of word representations in vector space”, arXiv: 1301.3781, Jan.), (2013.
-
H. Kang, and J. Yang, “The Analogy Test Set Suitable to Evaluate Word Embedding Model for Korean”, Journal of Digital Contents Society, 19, p1999-2008, Oct.), (2018.
[https://doi.org/10.9728/dcs.2018.19.10.1999]

-
J. Linck, and I. Cunnings, “The utility and application of mixed-effects models in second language research”, Language Learning, 65, p185-207, Jan.), (2015.
[https://doi.org/10.1111/lang.12117]

-
R. H. Baayen, D. H. Davidson, and D. M. Bates, “Mixed-effects modeling with crossed random effects for subjects and items”, Journal of Memory and Language, 59(4), p390-412, Mar.), (2008.
[https://doi.org/10.1016/j.jml.2007.12.005]

저자소개

2002 : Dept. of Computer Engineering, Dongguk University (M.S.)
1995 : Dept. of Mathematics, The University of Connecticut (Ph.D.)
2000~current: Associate Professor, Dept. of Computer Science & Engineering, Shinhan University
Interest Field: AI, Computational Linguistics, Big Data Computing, NLP