에지 검출을 위한 경량 확장 합성곱 신경망
Copyright ⓒ 2024 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
딥러닝 기반 에지 검출 방법들은 전통적인 방법에 비해 우수한 성능을 보이지만 보통 구조가 지나치게 복잡하며 과도한 연산 능력과 메모리 용량을 필요로 한다. 본 논문에서는 이를 개선하기 위해 파라미터 수가 아주 적은 네 종류의 합성곱 신경망 블록을 사용하여 유연하게 그 구조와 크기를 설정할 수 있는 경량 확장 합성곱 신경망을 제안하였다. 제안한 3단 신경망 기반의 에지 검출기를 BSDS500 데이터 셋을 사용하여 학습하고, F-지표의 관점에서 성능을 평가하였다. 결과적으로 파라미터 수가 기존 경량 신경망 기반 에지 검출기의 1/10 정도에 불과한 신경망을 사용하여 ODS와 OIS가 각각 0.771과 0.795인 같은 수준의 성능을 얻을 수 있었다. 또한 병렬 백본 구조를 사용한 경우에는 ODS와 OIS가 각각 0.802와 0.822로 향상되어, 가중치가 수십배나 많은 훨씬 복잡한 신경망을 사용한 에지 검출기와 대등한 성능을 보임을 확인하였다.
Abstract
Deep learning-based edge detection methods exhibit superior performance when compared to traditional methods; however, they typically require highly complex architectures, excessive computational power, and high memory capacity. In this paper, we propose a lightweight dilated convolutional network (LDCN) with flexible structure and size using four types of convolutional neural network blocks with a significantly small number of parameters. We trained the proposed three-stage neural network-based edge detector on the Berkeley Segmentation Data Set 500 and evaluated its performance in terms of the F-measure. Thus, we were able to achieve the same level of performance with optimal dataset scale (ODS) and optimal image scale (OIS) values of 0.771 and 0.795, respectively, using a neural network with approximately one-tenth the size of existing lightweight neural network-based edge detectors. Furthermore, with a parallel backbone structure, the ODS and OIS values were improved to 0.802 and 0.822, respectively, achieving superior performance equivalent to that of existing edge detectors that are based on significantly complex neural networks with tens of times more weights.
Keywords:
Edge Detection, Convolutional Neural Network, Dilated Convolution, Balanced Cross-Entropy, F-Measure키워드:
에지 검출, 합성곱 신경망, 확장 합성곱, 균형 교차 엔트로피, F-지표Ⅰ. 서 론
에지 검출 (edge detection)은 영상에서 서로 다른 두 개의 영역을 구분하는 고대비 경계를 찾는 작업이다. 이는 객체 분할[1],[2], 영상 인식[3],[4] 등 보다 복잡한 영상 처리나 컴퓨터 비전 작업은 물론, 의료영상 분석[5]이나 원격탐사[6] 분야에서도 초기 단계에 필요한 기본적인 과정이다.
그동안 에지 검출에 관한 많은 연구가 이루어졌지만 여전히 이 주제는 개방된 연구 분야이다. 현재의 주된 연구 동향 중 하나는 검출 정확도를 유지하면서 더 가벼운 심층 신경망(DNN: Deep Neural Network) 기반 에지 검출기를 개발하는 것이다. 특히 모바일 플랫폼 상에서는 연산량과 메모리 사용량을 줄일 수 있도록 신경망을 경량화하는 것이 더욱 중요하다.
DNN 기반 에지 검출기는 일반적으로 영상 분할이나 객체 인식과 같은 고수준 컴퓨터 비전 작업을 위해 설계된 신경망 구조를 채택하고 있다. 따라서, 이들은 수백만 개의 파라미터를 가진 대규모 신경망이 되는 것이 보통이다. 이에 비해 에지 검출은 상대적으로 지역적이며 비교적 간단한 작업이므로 지나치게 많은 파라미터나 복잡한 구조는 불필요할 수 있다.
본 논문에서는 낮은 복잡성과 적은 수의 파라미터를 가진 에지 검출기를 구현하기 위해 네 종류의 기본 구성 요소로 이루어진 합성곱 신경망(CNN: Convolutional Neural Network) 구조를 제안하였다. 기본 구성 요소인 각 블록은 적은 수의 파라미터를 가진 합성곱 층으로 구성되며 이 블록들의 조합에 따라 전체 신경망의 구조와 크기를 유연하게 설정할 수 있다.
II장에서는 에지 검출을 위한 전통적인 방법과 신경망 기반 방법 등 관련 연구들을 간략히 소개하고, III장에서는 본 논문에서 제안하는 신경망의 구조에 대해 구체적으로 설명하였다. IV장에서는 제안한 신경망의 학습에 필요한 손실함수, 데이터 셋, 평가 지표 등을 소개하고, V장에서는 BSDS500 (Berkeley Segmentation Data Set 500)[3] 데이터 셋을 이용한 실험을 수행한 후 그 결과를 기존의 신경망 기반 에지 검출기들과 비교하였다. 끝으로 VI장에서는 본 논문에서 제안한 방법이 기존의 CNN 기반 에지 검출기들에 비해 훨씬 적은 수의 파라미터만으로도 대등하거나 우수한 성능을 가진다는 결론을 제시하였다.
Ⅱ. 관련 연구
전통적인 비학습 기반 에지 검출에서는 영상의 1차 미분값의 최소값과 최대값을 구하거나 2차 미분값의 영교차(zero-crossing)를 구하여 에지를 검출한다. 영상의 1차 미분값을 사용하는 방법으로는 Sobel[7], Prewitt[8], Roberts[9], Canny[10] 에지 검출기 등이 있고, 2차 미분값을 사용하는 방법으로는 Laplacian 필터[11], Laplacian of Gaussian (LoG) 필터[12] 등이 있다.
이러한 방법들은 모두 영상의 밝기 값을 사용하여 불연속성을 찾는 데 기반을 두고 있다. 이중에서는 MSE (Mean Squared Error)와 PSNR (Peak Signal-to-Noise Ratio)의 관점에서 Canny 연산자가 가장 좋은 에지 검출기로 인정되고 있다[13].
최근에는 딥러닝 (deep learning) 기술의 발전으로 심층 신경망 기반의 에지 검출이 높은 정확도의 성능을 보이게 되었다. 에지 검출을 비롯한 영상 처리 분야에서는 데이터의 특성상 합성곱 신경망이 주로 사용된다.
지금까지 제안된 HED (Holistically-nested Edge Detector)[14], CED (Crisp Edge Detector)[15], BDCN (Bi-Directional Cascade Network)[16]과 같은 딥러닝 기반 에지 검출기들은 영상 분류 문제를 해결하기 위해 설계된 VGGNet (Visual Geometry Group Network)[17]를 백본 망 (backbone network)으로 사용한다. 따라서 이들은 영상 분류에 필요한 많은 특징들을 추출할 수 있지만, 이것이 에지 검출에 모두 필요하지는 않은 과도한 분량일 수 있다. 영상의 의미적 분할(semantic segmentation)에서는 특징 추출기가 다양한 객체 패턴을 인식할 수 있어야 하지만, 에지 검출에서는 에지와 비에지만 구별하여 인식하면 된다.
이점에 착안하여 제안된 TIN (Traditional Inspired Network)[18]과 FINED (Fast Inference Network for Edge Detection)[19]는 전통적인 에지 검출기의 기울기(gradient), 저역통과필터, 화소 연결(pixel connection)에 대응하는 세 가지 기본 모듈로 구성된 가벼운 CNN 기반 에지 검출기이다. 이들은 적은 수의 파라미터를 가진 신경망으로도 효과적으로 에지를 검출할 수 있음을 보였다.
Ⅲ. 제안하는 신경망 구조
본 논문에서는 적은 수의 파라미터를 가진 합성곱 층들로 구성된 블록들을 조합함으로써 전체 신경망의 구조와 크기를 유연하게 바꿀 수 있는 경량 확장 합성곱 신경망(LDCN: Lightweight Dilated Convolutional Network)을 제안한다.
이러한 구조는 기존의 신경망 구조와는 달리 다음과 같은 세가지 특징을 갖는다. 첫째, 블록을 구성 단위로 하여 모듈을 조립하는 방식으로 전체 신경망을 구성할 수 있기 때문에 합성곱 층 하나하나를 구성 단위로 하여 전체 신경망을 구성하는 것에 비해 구조적인 복잡성을 훨씬 줄일 수 있다. 둘째, 각 블록에 포함되는 합성곱 층의 수나 파라미터 수를 조정함에 따라 전체 신경망의 구조와 크기를 쉽게 바꿀 수 있기 때문에 최적의 구조와 크기를 찾아내는 데 유용하다. 셋째, 병렬 백본구조를 사용함으로써 기존의 경량 신경망 기반 에지 검출기보다 더 효율적으로 에지를 검출할 수 있다.
3-1 신경망의 전체 구조
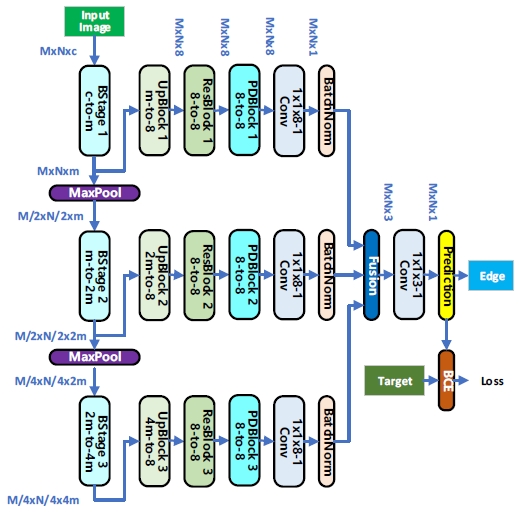
본 논문에서는 그림 1과 같이 3단으로 구성된 신경망을 제안한다. 그러나 필요에 따라서는 동일한 방식으로 단 수를 늘이거나 줄일 수 있다. 각 단은 다음에서 자세히 설명할 네 종류의 블록으로 구성된 동일한 구조로 되어 있다. 각 단을 구성하는 모든 블록은 3×3 커널을 가진 간단한 합성곱(convolution) 또는 전치 합성곱(transposed convolution) 층들로 이루어진다.
여기서 모든 블록과 그 내부의 모든 합성곱 층 및 전치 합성곱 층의 출력은 ReLU (Rectified Linear Unit) 활성화 함수를 통해서 얻어진다.
3-2 기본 구성 요소
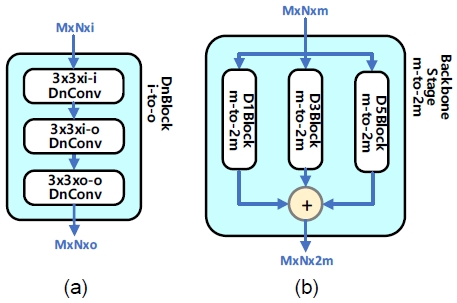
이 블록은 영상으로부터 특징을 추출하기 위하여 신경망 각 단 (stage)의 백본 (backbone)을 구성하는데 사용되며, 그림 2(a)와 같은 구조를 갖는다. 각 블록은 3개의 확장 합성곱 층으로 구성되며, 블록의 입력과 출력 채널 수는 각각 i와 o로 표시하였다. 영상을 입력 받는 제1단에서는 i = c(입력 영상 채널 수), o = m이고, 제2단부터는 o = 2i이다. 최경량 신경망에서는 m = 8이며, m 값을 16 또는 32로 설정함으로써 전체 신경망의 크기를 유연하게 조정할 수 있다.
이와 같이 3×3 커널의 확장 합성곱 층을 3층으로 구성하여 7×7 커널을 사용하는 효과를 얻을 수 있으며, 동시에 n =1, 3, 5 등의 계수를 갖는 확장 합성곱을 사용함으로써 수용영역 (receptive field)의 크기가 각각 3×3, 7×7, 11×11로 확장되는 효과를 얻을 수 있다. 계수가 1인 확장 합성곱 층은 보통의 합성곱 층을 의미한다.
그림 2(b)는 확장 계수가 각각 1, 3, 5인 백본 블록 3개를 묶은 백본 단 (backbone stage)을 보인 것이다. 단일 백본 블록이나 2개의 블록을 묶은 백본 단도 구성 가능하다. 이를 활용한 병렬 백본 망 구조가 LDCN의 가장 큰 특징이다.
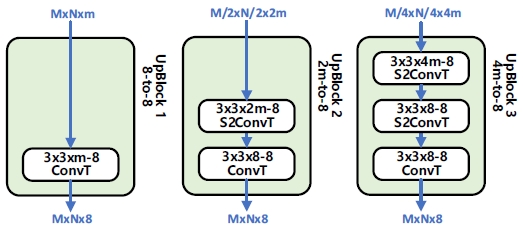
이 블록은 추출된 특징들을 에지 맵(edge map)으로 재구성하기 위한 디코딩을 수행한다. 그림 3은 왼쪽부터 제1, 2, 3단에 사용되는 업샘플링 블록을 보인 것이다. 입력 영상은 각 단의 백본을 지나면서 채널 수는 2배가 되지만 연산 간격 (stride)이 2인 최대 풀링 층을 지나면서 가로 및 세로 화소 수가 각각 반으로 감소하기 때문에 디코딩 과정에서 화소 수가 원영상과 동일하게 되도록 최대 풀링 층을 통과한 횟수만큼 업샘플링을 수행해야 한다.
디코딩과 업샘플링은 연산 간격이 2인 전치 합성곱을 통해 구현한다. 그러나 각 단의 업샘플링 블록의 입력은 최대 풀링 층 직전의 영상이므로 블록의 마지막 층에 연산 간격이 1인 전치 합성곱 층을 사용함으로써 마지막 층에서는 업샘플링이 수행되지 않도록 하였다. 또한, 이후 처리의 일관성을 위해 업샘플링 블록의 출력 채널 수는 8로 단일화하였다.
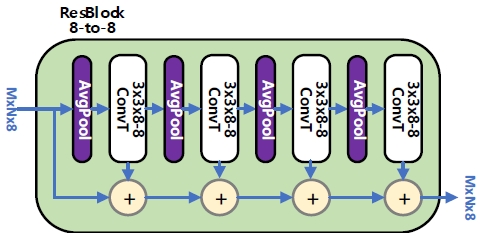
잔차 블록은 FINED의 구성 모듈 중 하나인 잔차 풀링(ResPool: Residual Pooling) 모듈[19]과 유사하나 디코딩 기능을 강화하기 위하여 합성곱 층 대신 전치 합성곱 층과 평균 풀링 층으로 구성하였다.
그림 4에 보인 바와 같이 4쌍의 평균 풀링 층 및 전치 합성곱 층을 통해 저역 통과 필터링 및 디코딩을 수행함으로써 배경이나 객체의 내부 영역에서 나타날 수 있는 미세한 텍스처 에지(texture edge)를 감소시키고 객체의 경계(boundary)에 해당하는 실제 에지는 보존하는 역할을 하게 된다.
백본 블록이나 업샘플링 블록은 신경망의 각 단마다 구조와 입출력 채널 수가 서로 다르지만 잔차 블록은 모든 단에 동일한 블록을 사용한다.
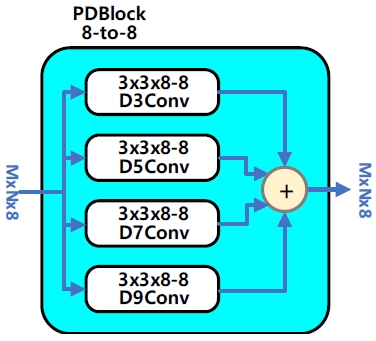
이 블록은 앞에서 디코딩 과정을 거쳐 생성한 다양한 크기의 에지 특징들을 수용할 수 있도록 그림 5와 같이 확장 계수가 각각 3, 5, 7, 9인 4개의 확장 합성곱 층으로 구성한다. 블록의 출력에서는 각 확장 합성곱 층의 출력을 집계하여 객체의 실제 경계에 해당하는 에지 영상을 생성하게 된다. 병렬 확장 합성곱 블록도 잔차 블록과 마찬가지로 모든 단에 동일한 블록을 사용한다.
3-3 기타 구성 요소
신경망의 각 단은 입력된 영상을 8-채널 1×1 커널을 가진 단일 합성곱 필터를 통해 단일 채널 영상으로 바꾼 후 배치 정규화(batch normalization)[20]를 거쳐 학습 데이터의 각 배치마다 데이터의 분포가 정규화된 출력을 생성한다. 각 단의 출력은 3-채널 영상으로 융합되어 다시 3-채널 1×1 커널의 단일 합성곱 필터를 통해 단일 채널 영상으로 변환된 후 배치 정규화를 거쳐 시그모이드(sigmoid) 함수에 의해 0과 1 사이의 확률값으로 표현되는 최종 에지 예측값을 생성한다.
Ⅳ. 신경망의 학습
입력 영상에 대하여 신경망의 출력에서 생성되는 에지 예측값은 다음 식으로 표시할 수 있다.
| (1) |
여기서 N(;)과 는 각각 신경망과 그 가중치를 나타내며, 는 예측 에지 맵, 는 입력 영상을 나타낸다. M과 N은 각각 영상의 총 화소 수와 신경망의 총 가중치 수이다.
입력 영상 X에 대해서 사전에 정의되어 있는 groundtruth 에지 맵을 라고 하면, 신경망의 학습은 threshold δ에 따라 예측 에지 맵의 각 화소 를 yi가 속한 에지 클래스 Y+나 비에지 클래스 Y-로 정확하게 분류하도록 가중치를 조정하는 과정이라고 할 수 있다. 여기서 Y+와 Y-는 다음 식으로 정의된다.
| (2) |
이때 0 < yi ≤ δ인 조건은 위치 i의 화소가 에지인지 비에지인지 분명하지 않을 경우를 의미한다. groundtruth 에지 맵을 정의할 때 여러 주석자들이 해당 화소를 에지 화소로 판단한 비율을 yi로 정한다면 모두의 의견이 일치하지 않을 경우에 이런 일이 생길 수 있다. 본 논문에서는 δ = 0.25로 설정하여 분명하게 분류하기 어려운 화소는 손실 함수에 반영하지 않음으로써 학습에서 제외한다.
4-1 손실 함수(Loss Function)
손실 함수는 신경망 학습을 좌우하는 결정적 요소이다. 에지 검출은 출력 영상의 화소들을 에지 화소(edge pixel) 클래스과 비에지 화소(non-edge pixel) 클래스로 나누는 이진 분류(binary classification) 문제라고 볼 수 있다. 그런데 에지 맵 영상에서 에지 화소 수는 비에지 화소 수에 비해서 현저히 적으므로 클래스 불균형이 존재한다. 이를 해결하기 위해서는 일반적으로 클래스 샘플 수의 역수에 비례하는 가중치를 부여하는 균형 교차 엔트로피(BCE: Balanced Cross-Entropy) 손실 함수 또는 가중 교차 엔트로피(WCE: Weighted Cross-Entropy) 손실 함수를 사용한다. 균형 교차 엔트로피 손실 함수[21]는 다음 식으로 정의된다.
| (3) |
여기서 σ(ㆍ)는 시그모이드 함수이며, α = |Y-|/|Y|, β = λ|Y+|/|Y|이고, 하이퍼 파라미터인 λ는 비에지 화소에 더 큰 가중치를 주어 텍스처 에지가 생기는 것을 억제할 수 있도록 1.1로 설정한다.
4-2 데이터 셋
제안한 신경망을 다른 신경망들과 비교하기 위하여 BSDS500 데이터 셋에 대한 성능 평가를 수행한다.
BSDS500 데이터 셋은 훈련(training) 영상 200개, 검증(validation) 영상 100개, 검사(test) 영상 200개로 이루어져 있으며 각 영상은 481×321 화소를 갖는다. 또한 각 영상별로 총 30명의 주석자가 1과 0으로 에지와 비에지를 구분하여 주관적으로 정의한 4~9개의 groundtruth 값이 포함되어 있다. 신경망의 훈련과 검증을 위해 이 값들을 평균하여 0과 1 사이의 확률값을 갖는 에지 맵 레이블을 생성하였다.
4-3 평가
다중 스케일 검사 방식이 더 나은 성능을 보인다는 이전의 연구 결과 [16], [22], [23]에 따라 본 논문에서도 입력 영상을 0.5, 1.0, 1.5 등 세 가지 서로 다른 스케일로 조정하여 신경망에 인가하고, 그 결과를 원영상의 크기로 재조정한 다음 평균을 취하여 출력 영상을 얻는다. 최종 예측 에지 맵을 얻기 위해서는 NMS (non-maximum suppression) 알고리즘 [14], [16], [22]를 사용하여 에지의 세선화(thinning) 과정을 거친다. 에지의 세선화 과정에서는 이진화를 위하여 threshold를 설정해야 하는데 여기에는 두 가지 방식이 있다. 하나는 데이터 셋의 모든 영상에 대해 단일 고정 threshold를 사용하는 ODS (optimal dataset scale) 방식이고, 다른 하나는 각 영상에 대한 최적의 threshold를 택하는 OIS (optimal image scale) 방식이다.
제안한 신경망의 성능을 평가하기 위한 지표로는 식 (4)와 같이 정밀도(precision)와 재현율(recall)의 조화 평균으로 정의되는 F-지표(F-Measure)를 사용한다.
| (4) |
여기서 정밀도와 재현율은 각각 다음과 같이 정의된다.
| (5) |
- et : 에지로 예측된 화소 중 실제 에지 화소 수
- nf : 에지로 예측된 화소 중 실제 비에지 화소 수
- ef : 비에지로 예측된 화소 중 실제 에지 화소 수
Ⅴ. 실험
5-1 실험 환경
본 논문에서 제시한 방법은 12GB 메모리를 갖는 단일 GPU (Graphics Processing Unit), NVIDIA GeForce RTX 3060 위에서 PyTorch로 구현하였다. 학습은 Adam (Adaptive moment estimation) 최적화[24]를 사용하여 크기가 3인 미니배치 방식으로 60 epochs 동안 진행하였다. 이때 학습율은 식 (6)과 같이 ηmax와 ηmin = 0.0001 사이에서 주기가 20 epochs인 코사인 함수 값으로 정해지는 CosineAnnealing 스케줄[25]에 따라 조정하였다.
| (6) |
식 (6)에서 최대 학습률 ηmax는 학습 결과에 큰 영향을 미치는 중요한 하이퍼 파라미터로서 반복적인 시도를 통하여 신경망의 구조와 크기에 따라 적절한 값으로 설정하였다.
총 60 epochs 동안 이러한 학습을 5차 반복하는데, 1차 학습에서의 신경망의 초기 가중치는 모두 평균값 0, 표준편차 0.01인 Gaussian 분포이며, 그 이후에는 바로 직전 학습된 가중치를 초기 가중치로 사용한다.
5-2 다양한 신경망 구조와 크기에 따른 성능 비교
본 논문에서 제안하는 LDCN 기반 에지 검출기는 Ⅲ장에서 설명한 3단 신경망이며, 학습에 사용할 BSDS500 데이터 셋은 모두 컬러 영상이므로 제1단의 입력 채널 수는 c = 3이다. 여기서 백본 단이 각각 1개, 2개, 3개의 백본 블록으로 구성되는 세 가지 유형의 신경망 모델을 정의하고, 이를 모델명에 첫 번째 식별자인 숫자로 추가한다. 이때 백본 단을 구성하는 백본 블록의 확장 계수는 순서대로 각각 n = 1, n = 1,3, n = 1,3,5이다.
그리고 각 유형에 대해서 백본 블록과 업샘플링 블록의 채널 수에 따른 세 가지 크기의 모델을 정의하였다. 제1단 백본 블록의 출력 채널 수는 순서대로 각각 m = 8, m = 16, m = 32이며, 이는 모델명에 두 번째 식별자인 알파벳으로 추가하였다. 이와 같이 백본 블록 및 업샘플링 블록의 구조와 크기에 따라 9가지 LDCN 기반 에지 검출기를 표 1과 같이 정의하였다.
9가지 신경망 모델을 위의 실험 조건에서 BSDS500으로 학습한 결과를 표 2에 정리하였다. 각 모델별 총 파라미터 수와 그에 따라 다르게 설정된 최대 학습률 ηmax 및 검사 영상 200개에 대한 학습 결과의 정량적 성능 지표인 ODS와 OIS F-지표값이 나와 있다.
표의 처음 세 행은 A형 LDCN 신경망을 기반으로 한 에지 검출기들의 성능이다. 총 파라미터 수는 1형, 2형, 3형이 각각 4만, 6만, 8만개이며, 파라미터 수가 증가함에 따라 성능도 눈에 띠게 향상됨을 볼 수 있다.
다음 세 행은 중간 크기인 B형 LDCN 신경망을 기반으로 한 경우이다. 이 경우도 백본 단의 병렬 백본 블록 수를 나타내는 1형, 2형, 3형으로의 변경에 따라서는 성능이 향상되지만, A형에서 B형으로의 변경에 의해서는 파라미터 수가 3배 정도 증가하는데 비해 성능 향상은 상대적으로 매우 적다. 이는 파라미터 수로 표현되는 신경망의 전체적인 규모보다는 특징 추출을 수행하는 백본 층의 구조가 더 중요한 요소로 작용하고 있음을 시사한다.
마지막 세 행은 파라미터 수가 가장 많은 C형 LDCN 신경망을 기반으로 했을 때의 결과이다. 마찬가지로 B형에 비해 파라미터 수가 3배 이상 증가했지만 2형과 3형의 경우는 B형에서 C형으로의 변경이 성능에 아무런 영향을 미치지 못한다. 뿐만 아니라 1형에서 2형으로의 변경에 의해서는 ODS가 0.782에서 0.799로, OIS는 0.805에서 0.820으로 성능이 개선되었지만, 2형에서 3형으로 구조를 변경할 경우에는 성능 개선이 나타나지 않는다. 따라서 에지 검출기로서의 신경망의 구조와 크기는 LDCN2C, LDCN2B 및 LDCN3B, LDCN3A 지점에서 거의 포화상태에 이른 것으로 판단할 수 있다.
이와 같은 내용은 ODS F-지표를 정밀도-재현도 그래프로 나타낸 그림 6에서도 확인할 수 있다. 그림 6(a)는 동일한 백본 구조를 가진 경우, 채널 수에 따른 성능을 비교한 것이고, 그림 6(b)는 동일한 채널 수를 가진 경우, 백본 망을 구성하는 병렬 백본 블록 수에 따른 성능을 비교한 것이다.
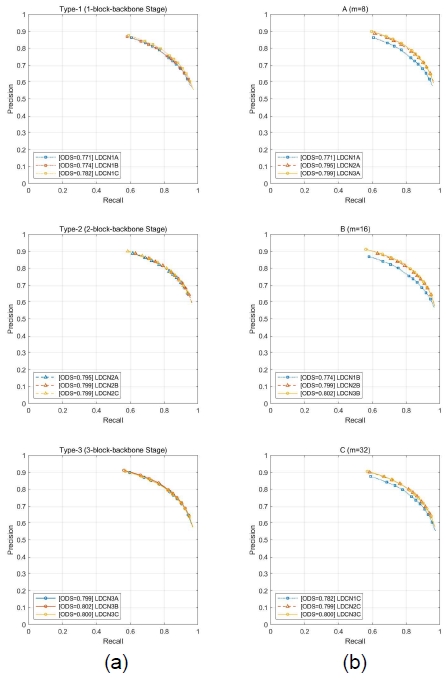
Precision-Recall Curve of proposed edge detectors on the BSDS500 dataset. (a) Comparisons according to the number of channels (b) Comparisons according to the number of backbone blocks
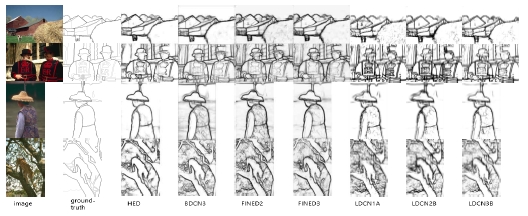
이상의 분석에 따라 가장 경량인 LDCN1A와 포화 성능에 도달한 LDCN2C, 그리고 성능이 가장 우수한 LDCN3B를 다른 에지 검출기와 비교하기 위한 대표적인 LDCN 기반 에지 검출기로 선정하였다. 이 세가지 대표 모델과 성능이 거의 포화된 또 다른 모델인 LDCN2B에 대해서 BSDS500 데이터 셋에 포함된 5가지 영상에 대해 에지 예측을 수행하여 얻은 에지 영상을 그림 7에 제시하였다. LDCN1A에서 나타나는 텍스처 에지들이 성능이 개선된 다른 3개의 모델에서는 많이 감소한 것을 볼 수 있다. 또한 정량적 평가에서는 LDCN3B가 가장 우수한 성능을 보였으나 평가자의 관점에 따라 영향을 받는 시각적 성능 평가에서는 많은 경우에 비에지를 더 억제한 결과를 보여 준 LDCN2C가 더 낫게 보일 수도 있을 것이다.
5-3 다른 에지 검출기와의 성능 비교
본 논문에서 제안한 에지 검출 신경망의 성능을 ODS 및 OIS F-지표의 관점에서 다른 방법들과 비교해 보았다. 표 3에 보인 바와 같이 비교 대상은 크게 두 그룹으로 나눌 수 있다. 하나는 신경망의 총 가중치가 1백만개 이상인 중량 그룹 H이고, 다른 하나는 총 가중치가 1백만개 이하인 경량 그룹 L이다.
T는 비신경망 기반의 전통적인 에지 검출기 그룹으로 모든 신경망 기반의 에지 검출기들의 성능은 이보다 매우 우수함을 알 수 있다. 이들 중에서는 Ⅱ장에서 언급한 바와 같이 Canny 에지 검출기가 ODS=0.639와 OIS=0.685로 성능이 제일 우수하다.
중량 그룹 H에 속하는 비교 대상 중 FINED3 이외의 에지 검출기들은 모두 고수준 영상 처리를 위한 신경망을 백본으로 채택하여 ODS와 OIS가 각각 0.788~0.817과 0.808~0.834 범위의 매우 우수한 성능을 보이고 있지만, 필요 이상으로 많은 가중치를 학습해야 하는 단점을 가지고 있다.
한편 경량 그룹 L에 속하는 비교 대상 에지 검출기로는 TIN1, TIN2 및 FINED2가 대표적인데, 전자에 비해 가중치 수가 매우 적어서 소요 메모리 용량 및 연산량의 측면에서 큰 장점을 가지고 있지만, ODS가 0.749~0.779 범위이고, OIS는 0.772~0.800 범위로서 성능은 다소 미흡하다.
본 논문에서 제안한 에지 검출기 중 LDCN1A는 그룹 L에 비해 1/2~1/10 정도의 적은 가중치를 가진 신경망을 기반으로 하고 있지만 ODS=0.771, OIS=0.795의 대등한 성능을 보이고 있다. LDCN2C의 성능 또한 ODS=0.799, OIS=0.820로서 가중치의 수는 경량 그룹 L에 해당하지만 중량 그룹 H에 속한 검출기와 유사한 수준의 성능을 나타내고 있다. 뿐만 아니라 LDCN3B의 가중치 수는 LDCN2C의 절반에도 미치지 못한다. 그러나 그 성능은 ODS=0.802, OIS=0.822로서 그보다 수십배 이상의 많은 가중치를 가진 신경망을 기반으로 한 그룹 H의 검출기들과 동일한 수준임을 알 수 있으며, 특히 FINED3에 비해 1/5 수준의 신경망을 기반으로 하고 있음에도 성능은 그보다 훨씬 우수함을 확인할 수 있다.
그림 8은 BSDS500 검사 영상에 대한 다양한 에지 검출기들의 예측 에지 맵을 시각적으로 비교한 것이다.
Ⅵ. 결 론
최근 딥러닝 기술의 발전에 힘입어 합성곱 신경망 기반의 에지 검출 방법들이 많이 발표되고 있다. 딥러닝 기반 에지 검출 방법들은 전통적인 방법에 비해 우수한 성능을 보이고 있지만 지나치게 복잡하고 과도한 연산 능력과 메모리 용량을 필요로 한다. 그러나 에지 검출은 상대적으로 저수준 영상 처리에 속하므로 경량의 신경망으로도 충분한 성능을 낼 수 있을 것이다.
본 논문에서는 백본 블록, 업샘플링 블록, 잔차 블록, 병렬 확장 합성곱 블록 등의 네 가지 기본 구성 요소로 구현할 수 있는 경량 3단 신경망 구조를 제안하였다. 각 블록은 3×3 커널을 가진 간단한 합성곱 또는 전치 합성곱 층으로 구성되며, 이 블록들의 조합에 따라 전체 신경망의 구조와 크기를 유연하게 설정할 수 있다. 특히 백본 단에 복수의 백본 블록을 사용한 병렬 백본 망은 제안하는 신경망 구조의 가장 큰 특징이라고 할 수 있다.
이를 토대로 낮은 복잡성과 적은 수의 파라미터를 가진 다양한 LDCN 기반 에지 검출기를 구현한 다음, BSDS500 데이서 셋을 사용하여 학습하고, F-지표의 관점에서 성능을 평가하였다.
기존의 경량 신경망 기반 에지 검출기에 비해 1/10 수준의 신경망을 사용한 경우에도 ODS와 OIS가 각각 0.771과 0.795로 같은 수준의 성능을 나타냈다. 또한 병렬 백본 구조를 사용한 경우에는 ODS와 OIS가 각각 0.802와 0.822로서, 가중치 수가 수십배인 훨씬 복잡한 신경망을 사용한 경우와 대등한 성능을 보임을 확인하였다.
결론적으로 본 연구의 의의는 다음과 같이 요약할 수 있다. 첫째, 블록 단위의 모듈로 구성됨으로써 구조적인 복잡성이 낮은 신경망 구조를 제안하였다. 둘째, 각 블록에 포함되는 합성곱 층의 수나 가중치의 수에 따라 전체 신경망의 구조와 크기를 간편하게 바꿈으로써 최적의 구조와 크기를 찾아내기가 수월하다. 셋째, 단순히 각 합성곱 층의 입출력 채널 수를 증가시키거나 단 수를 늘려서 신경망의 규모를 크게 하는 것보다는 백본 망을 병렬화하는 것이 성능을 훨씬 더 효율적으로 개선할 수 있음을 확인할 수 있었다.
본 논문에서 제안한 신경망 구조는 에지 검출과 같은 비교적 저수준의 작업에 적합한 구조이므로 객체 인식이나 영상 분할과 같은 고수준의 작업에는 적합하지 않을 수 있다. 그러나 이러한 신경망을 기반으로 한 에지 검출은 도로, 차량, 보행자 등의 경계를 찾아내어 자율 주행 차량을 제어하거나, 에지 정보를 기반으로 한 물체 추적 및 감지를 통해 보안 시스템의 효율성을 개선할 수 있으며, 조직이나 종양의 경계를 파악함으로써 진단 및 치료에 도움을 주거나 부품의 에지를 감지하여 제조 공정의 자동화에 기여할 수도 있다. 본 논문에서 제안한 신경망 구조는 이와 같은 에지 검출기의 기반이 되므로 그 활용 범위가 매우 넓다.
Acknowledgments
이 논문은 2021년도 강원대학교 대학회계의 지원을 받아 수행한 연구임.
References
-
D. G. Lowe, “Object Recognition from Local Scale-Invariant Features,” in Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, pp. 1150-1157, September 1999.
[https://doi.org/10.1109/ICCV.1999.790410]

- B. Javidi, Image Recognition and Classification: Algorithms, Systems, and Applications, New York, NY: Marcel Dekker, 2002.
-
P. Arbeláez, M. Maire, C. Fowlkes, and J. Malik, “Contour Detection and Hierarchical Image Segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 33, No. 5, pp. 898-916, May 2011.
[https://doi.org/10.1109/TPAMI.2010.161]

-
J. Shi and J. Malik, “Normalized Cuts and Image Segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22, No. 8, pp. 888-905, August 2000.
[https://doi.org/10.1109/34.868688]

-
R. Pourreza, Y. Zhuge, H. Ning, and R. Miller, “Brain Tumor Segmentation in MRI Scans Using Deeply-Supervised Neural Networks,” in Proceedings of the 3rd International MICCAI Brainlesion Workshop (BrainLes 2017), Quebec, Canada, pp. 320-331, September 2017.
[https://doi.org/10.1007/978-3-319-75238-9_28]

-
F. Isikdogan, A. Bovik, and P. Passalacqua, “RivaMap: An Automated River Analysis and Mapping Engine,” Remote Sensing of Environment, Vol. 202, pp. 88-97, December 2017.
[https://doi.org/10.1016/j.rse.2017.03.044]

- R. Jain, R. Kasturi, and B. G. Schunck, Machine Vision, New York, NY: McGraw-Hill, 1995.
- J. M. S. Prewitt, Object Enhancement and Extraction, in Picture Processing and Psychopictorics, New York, NY: Academic Press, ch. 4, pp. 75-149, 1970.
- L. Roberts, Machine Perception of Three-Dimensional Solids, in Optical and Electro-Optical Information Processing, Cambridge, MA: MIT Press, pp. 159-197, 1965.
-
J. Canny, “A Computational Approach to Edge Detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 8, No. 6, pp. 679-698, November 1986.
[https://doi.org/10.1109/TPAMI.1986.4767851]

- R. M. Haralick, Digital Step Edges from Zero Crossing of Second Directional Derivatives, in Readings in Computer Vision: Issues, Problem, Principles, and Paradigms, Los Altos, CA: Morgan Kaufmann Publisher, ch. 2, pp. 216-226, 1987.
-
A. Huertas and G. Medioni, “Detection of Intensity Changes with Subpixel Accuracy Using Laplacian-Gaussian Masks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 8, No. 5, pp. 651-664, September 1986.
[https://doi.org/10.1109/TPAMI.1986.4767838]

-
D. Poobathy and R. M. Chezian, “Edge Detection Operators: Peak Signal to Noise Ratio Based Comparison,” International Journal of Image, Graphics and Signal Processing, Vol. 6, No. 10, pp. 55-61, September 2014.
[https://doi.org/10.5815/ijigsp.2014.10.07]

-
S. Xie and Z. Tu, “Holistically-Nested Edge Detection,” International Journal of Computer Vision, Vol. 125, No. 1-3, pp. 3-18, December 2017.
[https://doi.org/10.1007/s11263-017-1004-z]

-
Y. Wang, X. Zhao, Y. Li, and K. Huang, “Deep Crisp Boundaries: From Boundaries to Higher-Level Tasks,” IEEE Transactions on Image Processing, Vol. 28, No. 3, pp. 1285-1298, March 2019.
[https://doi.org/10.1109/TIP.2018.2874279]

-
J. He, S. Zhang, M. Yang, Y. Shan, and T. Huang, “BDCN: Bi-Directional Cascade Network for Perceptual Edge Detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 44, No. 1, pp. 100-113, January 2022.
[https://doi.org/10.1109/TPAMI.2020.3007074]

-
K. Simonyan and A. Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition,” arXiv:1409.1556v1, , September 2014.
[https://doi.org/10.48550/arXiv.1409.1556]

-
J. K. Wibisono and H.-M. Hang, “Traditional Method Inspired Deep Neural Network for Edge Detection,” in Proceedings of 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, UAE, pp. 678-682, October 2020.
[https://doi.org/10.1109/ICIP40778.2020.9190982]

-
J. K. Wibisono and H.-M. Hang, “FINED: Fast Inference Network for Edge Detection,” in Proceedings of 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, pp. 1-6, July 2021.
[https://doi.org/10.1109/ICME51207.2021.9428230]

-
S. Ioffe and C. Szegedy, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift,” arXiv:1502.03167, , February 2015.
[https://doi.org/10.48550/arXiv.1502.03167]

-
T. H. Phan and K. Yamamoto, “Resolving Class Imbalance in Object Detection with Weighted Cross Entropy Losses,” arXiv:2006.01413, , June 2020.
[https://doi.org/10.48550/arXiv.2006.01413]

- Y. Liu, M.-M. Cheng, X. Hu, K. Wang, and X. Bai, “Richer Convolutional Features for Edge Detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu: HI, pp. 3000-3009, July 2017.
-
R. Deng, C. Shen, S. Liu, H. Wang, and X. Liu, “Learning to Predict Crisp Boundaries,” in Proceedings of the 15th European Conference on Computer Vision (ECCV 2018), Munich, Germany, pp. 570-586, September 2018.
[https://doi.org/10.1007/978-3-030-01231-1_35]

-
D. P. Kingma and J. Ba, “Adam: A Method for Stochastic Optimization,” arXiv:1412.6980v1, , December 2014.
[https://doi.org/10.48550/arXiv.1412.6980]

-
I. Loshchilov and F. Hutter, “SGDR: Stochastic Gradient Descent with Warm Restarts,” arXiv:1608.03983v1, , August 2016.
[https://doi.org/10.48550/arXiv.1608.03983]

-
A. Al-Amaren, M. O. Ahmad, and M. N. S. Swamy, “RHN: A Residual Holistic Neural Network for Edge Detection,” IEEE Access, Vol. 9, pp. 74646-74658, May 2021.
[https://doi.org/10.1109/ACCESS.2021.3078411]

저자소개

1981년:서울대학교 전자공학과(공학사)
1983년:서울대학교 전자공학과(공학석사)
1988년:서울대학교 전자공학과(공학박사)
1988년~현 재: 강원대학교 전기전자공학과 교수
2014년~현 재: 한국디지털콘텐츠학회 종신회원
※관심분야:영상처리, 딥러닝