농산물 가격의 특이치 탐지 및 처리를 통한 딥러닝 기반 가격 예측

Ⅰ. 서 론

농산물 가격은 일반 제품 가격과는 달리 높은 변동성을 가지고 있다. 농산물 가격의 변화에 있어 특이한 상황이 탐지되었을 때, 농산물의 양을 적절히 조절하는 정책 등으로 공급 조절을 한다면 소비시장에서의 가격 안정을 도모할 수 있을 것다. 이러한 측면에서 농산물 가격 예측은 시장경제에서 중요한 의의가 있다. 농산물의 낮은 가격은 농민의 소득을 줄이게 되고, 높은 가격은 소매 소비자의 가계 비용을 증가시킬 수 있다[1].

국내 친환경 농산물 및 식품의 시장 규모는 2018년에는 1조 2868억 원, 2019년에는 1조 8354억 원을 기록했고 2020년 약 1조 9000억 원으로 추정했고, 2025년에는 2조 1360억 원에 이를 것으로 전망했다. 농산물의 시장 규모가 크게 늘어나고 있어 농산물 가격 변동 예측 관련 연구는 경제 발전을 위해 연구의 필요성이 있다. 이에 관한 농산물 가격 예측 연구가 활발히 진행되고 있다[1]-[4]. 또한, 가격 변동에 대한 예측 연구로 주식 가격 변동 예측에 관한 딥러닝 기법 적용에 관한 연구가 있다[5],[6].

농산물의 가격 변동은 주식 등 일반 제품의 가격 변동과는 달리 수확 시기에 공급량이 늘어서 가격이 하락하거나, 추석이나 설 명절 등 특별한 기간에 수요량이 대량으로 증가하여 가격이 상승하게 되는 요인이 있다. 그리고 급격한 기상변화와 자연재해 그리고 병충해 등으로 인해 갑작스러운 가격 상승 또는 하락 등의 변동이 나타난다. 이와 같이, 어떤 데이터가 일반적인 전체 분포에서 벗어나서 어떤 값이 다른 값들에 비해 비정상적으로 크거나 작은 값을 나타내는 데이터를 특이치(outlier)라고 한다.

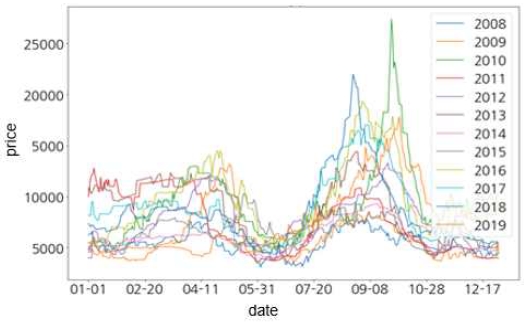
농산물 가격의 변동을 전 년과 전 월 또는 전 주와 비교하여 가격 변동을 예측하기는 어렵다. 왜냐하면, 전 년의 데이터 또한 데이터 분포에서 매우 낮거나 높은 특이치를 가지고 있을 수 있기 때문에 단순히 비교함으로써 변동을 예측하는 것은 잘못 분석할 수 있다. 예를 들어, 2010년에는 농산물 중에서 배추의 작황이 특히 좋지 않아서, 공급이 불안정하게 되었고, 그로 인해 배추의 가격이 폭등한 사례가 있다. 그림 1에서 보는 것과 같이, 2010년 9월부터 10월까지의 가격이 큰 폭으로 올라간 것을 볼 수 있다. 이는 농산물 가격 변동 데이터에서 특이치를 탐지하고 처리하는 것은 중요하다는 것을 보여준다[4],[8].

Fig. 1.

Price fluctuation graph (Napa Cabbage)

이러한 관찰을 통해서, 농산물 품목에 따른 수확시기, 명절, 물가 상승률 등과 같이 일정하게 발생하는 추세와 계절성을 근거로 하여 가격의 특정 기준으로 정하고 특이치를 탐지한다면 가격에 대한 예측을 보다 더 잘할 수 있을 것으로 본다.

특이치는 데이터의 편향을 발생시켜 학습하고 예측하는데 어려움이 있다. 농산물가격의 특이치는 갑작스런 자연재해나 기온의 변화로 발생한다. 또 농산물은 모종시기와 수확시기 등의 계절성이 있어 보통 연도별로 규칙적인 데이터의 변화가 있어 이에 따라 특이치를 탐지해야 하는 어려움이 있다.

특이치를 탐지하는 방법도 전체 데이터의 기준이 아닌 데이터의 이동에 따라 탐지하고 처리하는 것이 중요하다. 따라서, 본 연구에서는 농산물 가격 변동에 대해 계절성을 포함하여 월별 사분위수 특이치를 탐지하고 이동평균법의 범위를 한정하여 특이치에 대한 처리를 한다. 그리고, 농산물 가격 변동 예측 모델을 특이치 탐지와 처리 방법으로 전처리한 기준으로 학습하고 특이치가 아닌 구간과 특이치 구간을 구분한 예측 모델을 통해 딥러닝 기반 예측 성능을 향상시킬 수 있도록 한다.

본 논문의 구성은 다음과 같다. 2장에서는 특이치 탐지와 가격 예측에 관한 기존의 연구를 소개하고, 3장에서는 농산물 가격 변동에서의 특이치 탐지 기법을 제안한다. 4장에서 탐지된 특이치를 처리한 정상 시계열데이터에서의 딥러닝 기반 가격 예측을 한다. 5장에서는 특이치 탐지 실험과 가격 예측에 대한 성능을 비교 분석한다. 6장에서 결론을 맺는다.

Ⅱ. 관련 연구

Ⅲ. 농산물 가격 특이치 탐지

이 장에서는 농산물 가격 변동 데이터의 계절성 등의 특성을 고려하여 사분범위를 이용하여 일정한 구간으로 나누어 특이치 구간을 탐지하고, 시계열 데이터(time series)에서 비정상적(non-stationary)인 시계열 데이터를 정상(stationary)적인 시계열 데이터로 변환한 후 특이치를 탐지하는 방법을 제안한다.

3-1 계절성을 반영한 특이치 구간 탐지

기존의 특이치 탐지 연구에서 보편적으로 많이 사용하는 방법은 사분위수 범위(InterQuartile Range; IQR)를 이용한 상자수염그림(Box-and-whisker plot) 방법[17]이다. 이는 제1사분위수와 제3사분위수 사이 범위인 사분범위(IQR)를 이용하여 IQR 값에 1.5를 곱한 값보다 크거나 작은 값인지 확인한다.

본 연구에서는 농산물 가격 데이터의 특성을 고려하여 월별 기간으로 기준을 나누어 사분위를 적용한다. 또한 계절성의 특징을 가진 농산물 가격 변동 데이터를 기간별로 특이치를 탐지하여 계절성의 특징을 완화하여 탐지한다.

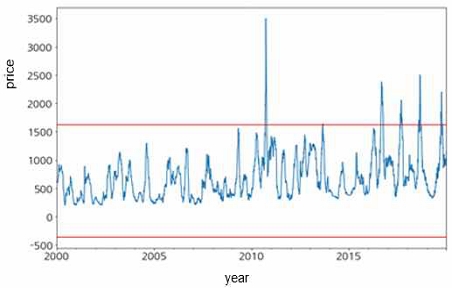
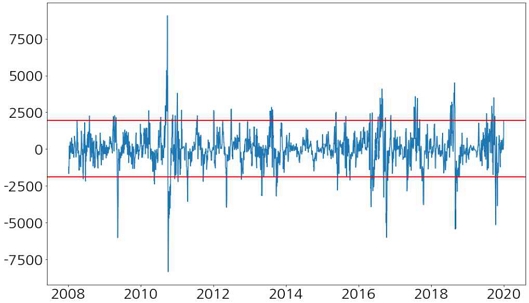
그림 2는 배추 가격 변동 데이터에 대한 기존 사분위수 특이치 탐지를 표현한 것이다. 아래외 위의 빨간색 선 범위 밖의 값들을 특이치로 탐지한다. 배추 가격은 계절에 따라 즉, 모종기간이나 수확기간에 따라 가격의 변동에 있어서 차이가 크게 나는 것을 확인할 수 있다. 이는 수확 기간 또는 모종 심는 기간이 특이치로 표현된 것으로 기존 사분위수 특이치 탐지 방법의 한계를 나타내는 것이다. 즉, 배추의 가격 변동에 있어서는 9월의 가격에 비해 6월의 가격이 전반적으로 낮은 가격이라는 것을 볼 수 있다. 그런데, 6월의 가격 변동에 있어서 특이치가 생기는 경우, 기존의 특이치 탐지 방법으로는 탐지할 수 없다. 반면, 9월의 가격 변동에 있어서는 특이한 상황이 아닌데도 특이치로 탐지될 수 있다.

Fig. 2.

Traditional quartile outlier detection

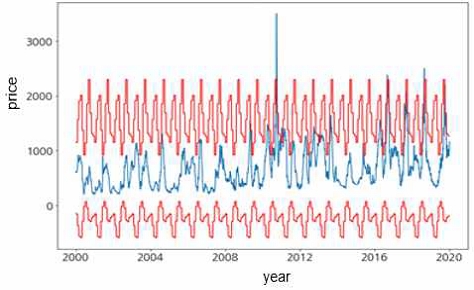
그림 3은 본 연구에서 제안하는 월별 사분위수로 특이치를 탐지한 것을 나타낸다. 배추 가격 데이터를 월별로 구간을 나누어 특이치 구간을 탐지하여 계절성을 가진 데이터의 계절성을 반영하여 특이치를 탐지할 수 있다. 실험 결과 분석을 통해 기존방법(그림 2)에서는 특이치가 135개 탐지되는 것을 제안방법(그림 3)에서는 9월에서 10월까지의 계절성을 반영하여 특이치 탐지가 많이 줄어들어 특이치를 59개 탐지하는 것을 볼 수 있다.

Fig. 3.

Proposed monthly quartile outlier detection

농산물 품목마다 모종 심는 기간과 수확 기간이 다르므로, 그 기간을 따로 반영하여 특이치를 판단하는 것이 보다 정확할 수 있으나 다양한 품목에 같이 적용할 수 있는 방법인 월별로 기간을 나누었다.

3-2 정상 시계열 데이터로 변환하여 특이치 탐지

정상((stationary) 시계열은 정상성을 가진 시계열 데이터이다. 통계적 특성을 나타내는 평균과 분산이 시점이 다르더라도 일정한 성질을 갖는 것을 정상성이라 한다. 따라서 농산물 가격 데이터에서 계절성의 특징을 제거하여 정상성을 갖는 데이터로 변환함으로써 보다 객관적인 특이치를 탐지할 수 있다. 비정상(non-stationary) 시계열은 시계열 데이터의 일정 기간의 평균을 나타내는 수준이 시점에 따라 달라지는 특징이 있고, 계절성이나 추세를 가지는 경우에는 진동 폭도 달라진다는 특징이 있다.

Box 등[18]은 확률적 추세를 지닌 비정상 시계열 데이터의 경우, 두 값을 뺀 차이를 계산하는 차분 연산(difference operation)을 통해서 추세를 제거하고 정상 시계열로 변환하는 방법을 제시하였다. Cleveland 등[19]은 n차 차분 연산을 이용하여 추세나 계절성을 제거하였다. Loess를 사용한 계절성과 추세 분해(Seasonal Trend decomposition using Loess; STL) 기법을 이용하여 주기를 확인하였다.

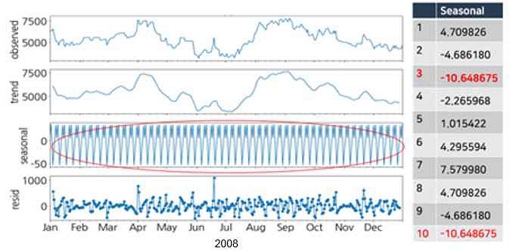
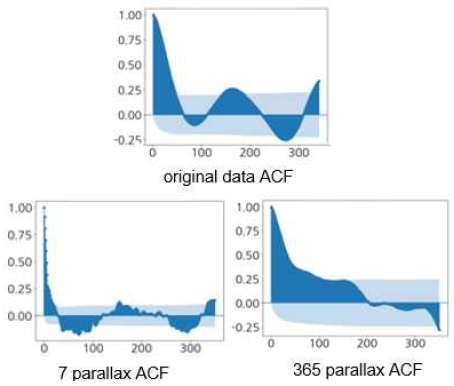
본 연구에서도 농산물 가격 데이터에 대해 시계열 분석을 위해서 차분 연산을 이용해 비정상 시계열 데이터를 정상 시계열 데이터로 변환한다. 그림 4는 배추 가격에 대한 STL 시계열 분해를 나타낸 것으로, 계절성(Seasonal)이 7 시차이고, 추세와 주기를 제외한 나머지(Resid) 부분을 확인할 수 있다. 또 농산물 데이터의 가격 특징은 수확시기와 명절 등 1년을 주기로 하는 계절성을 가지므로, 365 시차 차분도 확인할 수 있다. 365 시차 차분 연산 개념은 흔히 언론 보도에서 전년도 가격과 비교하는 방법이다.

Fig. 4.

STL Time Series Decomposition

정상성 검증을 통해 정상 시계열 데이터임을 확인하기 위해 자기상관(AutoCorrelation Function; ACF) 값으로 시각적으로 확인하였다. 정상 시계열 데이터는 시각적으로 ACF 값이 비교적 짧은 시차에 0으로 떨어지는 것으로 확인할 수 있다. 그림 5에서 배추 가격에 대한 7 시차 차분과 365 시차 차분을 통해 ACF 값을 구하면 7 시차 차분 연산이 정상성을 가진다는 것을 볼 수 있다.

Fig. 5.

Price autocorrelation (ACF)

또한, 시계열 데이터가 정상성을 가지는지를 판단하기 위해, 단위근 검정(unit root test) 방법인 ADF(Augmented Dickey-Fuller) 검정법을 이용한다[20]. 본 실험에서는 농산물 가격 데이터에서 배추뿐만 아니라 무, 양파 가격에 대해서도 7 시차 차분에서 p-value가 0.05 이하를 나타내므로 정상성을 나타내는 시계열임을 확인할 수 있었다.

정상 시계열 데이터에서는 시점이 다르더라도 통계적 특성이 일정하므로 월별 구간으로 나눌 필요가 없으므로, 본 연구에서는 그림 6과 같이 정상 시계열로 변환한 데이터에 대해서 기존의 사분범위를 적용하여 특이치 구간을 탐지하였다 .

Fig. 6.

Outlier interval detection for stationary time series data

Ⅳ. 특이치 처리를 통한 딥러닝 기반 가격 예측

Ⅴ. 실험 및 평가

5-1 실험 데이터

본 연구에서 사용한 실험 데이터는 표 1에 나타나 있다. 농산물유통정보(Korea Agricultural Marketing Information Service; KAMIS)에서 공개한 농산물 가격 데이터를 이용하였다. KAMIS 사이트(http://kamis.or.kr)의 오픈API(Application Programming Interface)를 이용하여 2006년부터 2019년까지 14년 동안의 일일 가격 변동 데이터를 수집하였다.

Table 1.

Experimental dataset

도매업체의 일일 가격 데이터가 제공되고 있는 품목 중 채소류에 대해 모든 기간에 대해 데이터가 존재하는 품목은 16개이다. 품목 형태는 품목그룹명(채소류)-품목명(배추)-품종명(봄배추)라고 상세화 되어 있다. 본 실험을 위해 품목명(배추)로 평균 가격으로 대체하였다. 품종별 큰 가격 차이가 나는 상품은 공정성을 위해 제외하였다. 상품의 등급은 상품, 중품으로 나뉘어져 있는데 두 개의 그룹의 흐름이 비슷하여 비교를 위해 상품 등급의 가격으로 정하였다.

본 연구에서의 실험은 일일 가격 데이터로, 가격 정보가 연속적으로 있어야 하는데 농산물유통 가격 데이터에는 공휴일과 주말의 값이 존재하지 않아 선형보간법을 이용하여 결측값을 대체하였다. 즉, 데이터 전처리로 결측값 바로 이전과 이후의 유효한 값의 중간값으로 대체하였다. 본 연구의 실험에 사용한 농산물 품목은 배추, 무, 양파이다.

5-2 특이치 탐지 실험 결과

특이치 탐지 비교 실험을 위해 기존 사분위수 특이치 탐지 결과, 365시차 차분, 월별 사분 범위 특이치 탐지, 그리고 제안 방법인 월별사분범위 탐지에 대해 정상시계열 데이터로 변환 후 특이치를 탐지한 결과가 표 2에 나타나 있다.

Table 2.

Outlier detection comparison experiment results

본 실험 결과에서는 김장철에 많은 수요가 있는 배추와 무의 가격 변동 그래프가 매우 유사하게 나타났다. 그러나 무의경우 가격 상승폭이 배추보다 크게 발생하여, 비정상 시계열 데이터에서 특이치를 올바르게 탐지하지 못하는 문제가 발생했다. 이로 인해 배추와 무의 특이치 탐지 개수에 차이가 발생하게 되었다. 또한, 양파의 특이치 탐지 결과에서는 최대 3만원까지 아주 큰 폭으로 자주 상승하는 현상이 있어서, 365 시차 단위로 비교하게 되면 가격 변동의 특이치를 잘못 탐지하거나 탐지가 되지 않았다.

본 연구에서의 비정상 시계열 데이터에 대한 기존의 특이치 탐지보다 사분범위 월별 구간을 변형하여 처리함으로써 특이치에 대한 의미 있는 탐지가 가능해졌음을 알 수 있다. 본 연구에서 제안한 방법에서는 계절성을 제거하고 특이치를 탐지하여 정상 시계열 데이터로 변환한 것에 대한 탐지에서는 다른 방법에서 탐지하지 못한 것을 탐지할 수 있었다. 특이치 탐지에 대한 실험 결과의 영향은 특이치 처리를 통한 가격 예측 실험에서 그 효과를 확인할 수 있다. 본 연구는 특이치 탐지[23]를 확장한 특이치 처리 및 예측 연구이다.

5-3 가격 예측 실험 결과

가격 예측을 위한 실험 데이터는 표 3에 나타나 있다. 모델 파라미터 설정을 위하여 학습데이터로 2006년부터 2016년까지의 11년간의 데이터를 이용하였고, 검증을 위한 데이터는 2017년 1년간의 데이터, 테스트 데이터는 2018년 1년간 데이터를 이용하여 각 예측 모델의 성능을 비교 평가하였다.

Table 3.

Experiment data for price prediction

성능측정 방법으로는 평균 제곱근 오차(RMSE; Root Mean Square Error)과 평균 절대비 오차(MAPE; Mean Absolute Percentage Error)를 사용하였다. RMSE는 크기 의존적 오류율을 표현하는 것이고, MAPE는 비율 오류율을 표현하는 것이다.

$\[ RMSE=\sqrt{\frac{\sum _{i=0}^n{\left({ True}_i-{ \text{Pr}ediction}_i\right)}^2}{n}} \]$

(1)

$\[ MAPE =\frac{1}{n}\sum _{i=1}^n\frac{\left|{ True}_i-{ \text{Pr}ediction}_i\right|}{{ True}_i}\times 100 \]$

(2)

농산물 가격 예측 모델의 비교 실험 방법은 다음과 같다.

• - ARIMA: 통계 모델인 ARIMA 모델 기반 예측
• - Prophet: 시계열 예측 모델인 Prophet 기반 가격 예측
• - LSTM: 비정상 시계열 데이터에 대한 LSTM 모델 기반 가격 예측
• - 제안 방법(Proposed): 특이치 탐지 및 처리를 통한 정상시계열 데이터 변환 후 LSTM 모델 기반 가격 예측

농산품 배추, 무, 양파에 대해 가격 예측 모델에 대한 비교실험 결과는 표 4에 나타나 있다. 또한, 실험 데이터(학습/개발/테스트)의 데이터 기간을 다르게 한 경우에 대한 비교실험에서도 제안한 특이치 탐지 및 특이치 처리를 통한 LSTM 모델이 더 좋은 성능이 보임을 확인하였다.

Table 4.

Price prediction comparison experiment results

Table 5.

Price prediction experiment results by data period

본 연구에서 제안한 특이치 탐지 및 처리를 통한 정상 시계열 데이터에서의 가격 예측 방법이 절대비 오차(MAPE)와 평균제급근 오차(RMSE)에 대해서 성능이 제일 좋음을 확인할 수 있다.

VI. 결 론

본 연구에서는 농산물의 가격 변동 데이터에 대한 가격 예측을 위해 계절성을 반영하여 특이치 탐지를 하고, 그에 대한 처리를 통해서 비정상 시계열 데이터를 정상 시계열 데이터로 변환한 후 딥러닝 기반 가격 예측 방법을 제안하였다. 비정상시계열 데이터에서의 특이치 탐지를 위한 기존의 사분범위를 월별 구간으로 변형하고, 이동평균법을 이용하여 특이치를 처리하여 정상시계열 데이터로 변환한 것에 대한 특이치 탐지는 기존의 방법에서 탐지하지 못하는 부분까지 탐지가 가능했다. 농산물 일일 가격 데이터에 대한 가격 예측 방법인 ARIMA 모델, Prophet 모델과 비정상 시계열데이터에서의 LSTM 모델과 제안한 방법의 LSTM 모델 적용의 비교 실험을 통해서 제안한 방법이 평균제곱급 오차와 평균 절대비 오차에서 가격 예측에 유효함을 확인하였다.

향후 연구를 통해 농산물 품목에 따른 파종 및 수확 시기 등을 반영한 특이치 탐지는 더 정밀한 가격 예측에 도움이 될 것으로 기대된다.

Acknowledgments

본 연구는 2020년 한국정보화진흥원의 농식품 빅데이터 플랫폼 및 센터 구축 사업의 지원을 받아 수행된 기초연구입니다.

References

• T.-W. Woo and I.-S. Oh, “Time Series Forecasting of Agricultural Products’ Sales Volumes Based on Seasonal Long Short-Term Memory,” Applied Sciences, Vol. 10, No. 22, 8169, November 2020. [https://doi.org/10.3390/app10228169]
• L. Nassar, I. E. Okwuchi, M. Saad, F. Karray, and K. Ponnambalam, “Deep Learning Based Approach for Fresh Produce Market Price Prediction,” in Proceedings of 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, pp. 1-7, July 2020. [https://doi.org/10.1109/IJCNN48605.2020.9207537]
• J. Kim and J.-I. Lee, “A Study on Agricultural Price Prediction System Based on Deep Learning,” Journal of Korean Institute of Information Technology, Vol. 17. No. 6, pp. 27-34, June 2019. [https://doi.org/10.14801/jkiit.2019.17.6.27]
• V. Jadhav, B. V. Chinnappa Reddy, and G. M. Gaddi, “Application of ARIMA Model for Forecasting Agricultural Prices,” Journal of Agricultural Science and Technology, Vol. 19, No. 5, pp. 981-992, September 2017.
• K. Kohara, T. Ishikawa, Y. Fukuhara, and Y. Nakamura, “Stock Price Prediction using Prior Knowledge and Neural Networks,” Intelligent Systems in Accounting, Finance and Management, Vol. 6, No. 1, pp. 11-22, March 1997. [https://doi.org/10.1002/(SICI)1099-1174(199703)6:1<11::AID-ISAF115>3.0.CO;2-3]
• J. W. Lee, “Stock Price Prediction Using Reinforcement Learning,” in Proceedings of 2001 IEEE International Symposium on Industrial Electronics, Pusan, pp. 690-695, June 2001. [https://doi.org/10.1109/ISIE.2001.931880]
• D. C. Hoaglin, B. Iglewicz, and J. W. Tukey, “Performance of Some Resistant Rules for Outlier Labeling,” Journal of the American Statistical Association, Vol. 81, No. 396, pp. 991-999, 1986. [https://doi.org/10.2307/2289073]
• R. Fried, “Robust Filtering of Time Series with Trends,” Journal of Nonparametric Statistics, Vol. 16, No. 3-4, pp. 313-328, 2004. [https://doi.org/10.1080/10485250410001656444]
• J. I. Choi, I. O. Um, and H. J. Cho, “Outlier Detection in Time Series Data,” The Korean Journal of Applied Statistics, Vol. 29, No. 5, pp. 907-920, August 2016. [https://doi.org/10.5351/KJAS.2016.29.5.907]
• H. Fu, H. Ma, and A. Ming, “EGMM: An Enhanced Gaussian Mixture Model for Detecting Moving Objects with Intermittent Stops,” in Proceedings of 2011 IEEE International Conference on Multimedia and Expo, Barcelona, Spain, pp. 1-6, July 2011. [https://doi.org/10.1109/ICME.2011.6012011]
• J. Ramakrishnan, E. Shaabani, C. Li, and M. A. Sustik, “Anomaly Detection for an E-commerce Pricing System,” in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD ’19), Anchorage: AK, pp. 1917-1926, August 2019. [https://doi.org/10.1145/3292500.3330748]
• L. Madaan, A. Sharma, P. Khandelwal, S. Goel, P. Singla, and A. Seth, “Price Forecasting & Anomaly Detection for Agricultural Commodities in India,” in Proceedings of the 2nd ACM SIGCAS Conference on Computing and Sustainable Societies(COMPASS ’19), Accra, Ghana, pp. 52-64, July 2019. [https://doi.org/10.1145/3314344.3332488]
• F. T. Liu, K. M. Ting, and Z.-H. Zhou, “Isolation Forest,” in Proceedings of 2008 8th IEEE International Conference on Data Mining, Pisa, Italy, pp. 413-422, December 2008. [https://doi.org/10.1109/ICDM.2008.17]
• S. Siami-Namini, N. Tavakoli, and A. S. Namin, “A Comparison of ARIMA and LSTM in Forecasting Time Series,” in Proceedings of 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando: FL, pp. 1394-1401, December 2018. [https://doi.org/10.1109/ICMLA.2018.00227]
• S. Shin, M. Lee, and S. Song, “A Prediction Model for Agricultural Products Price with LSTM Network,” The Journal of the Korea Contents Association, Vol. 18, No. 11, pp. 416-429, November 2018. [https://doi.org/10.5392/JKCA.2018.18.11.416]
• K.-T. Bae and C.-J. Kim, “An Agricultural Estimate Price Model of Artificial Neural Network by Optimizing Hidden Layer,” Journal of Korean Institute of Information Technology, Vol. 14, No. 12, pp. 161-169, December 2016. [https://doi.org/10.14801/jkiit.2016.14.12.161]
• J. W. Tukey, Exploratory Data Analysis, San Diego, CA: Pearson, pp. 131-160, 1977.
• G. E. P. Box and G. M. Jenkins, Time Series Analysis: Forecasting and Control, San Francisco, CA: Holden-Day, 1970.
• R. B. Cleveland, W. S. Cleveland, J. E. McRae, and I. Terpenning, “STL: A Seasonal-Trend Decomposition Procedure Based on Loess,” Journal of Official Statistics, Vol. 6, No. 1, pp. 3-33, 1990.
• W. A. Fuller, Introduction to Statistical Time Series, New York, NY: John Wiley & Sons, 1976.
• S. Hochreiter and J. Schmidhuber, “Long Short-Term Memory,” Neural Computation, Vol. 9, No. 8, pp. 1735-1780, November 1997. [https://doi.org/10.1162/neco.1997.9.8.1735]
• S. J. Taylor and B. Letham, “Forecasting at Scale,” The American Statistician, Vol. 72, No. 1, pp. 37-45, 2017. [https://doi.org/10.1080/00031305.2017.1380080]
• C. Park and K.-S. Lee, “Outlier Detection in the Agrifoods Product Price,” in Proceedings of 2020 Korea Software Congress, Online, pp. 565-567, December 2020.