허용 지연 시간을 갖는 실시간 화상 감시 카메라 시스템의 최적 구성 연구

Ⅰ. 서 론

화상 기반의 감시 시스템은 폐쇄회로텔레비전(CCTV) 방식 시스템에서부터 웹카메라, PTZ (pan-tilt-zoom) 기능을 탑재한 지능형 카메라, 사설 네트워크 또는 공용 네트워크 기반의 감시 카메라 네트워크 등 다양한 형태로 발전되어 오고 있다[1]. 특히 네트워크 기반 감시 카메라 시스템은 중앙 감시 센터가 지역별로 설치된 여러 개의 카메라로부터 화상 정보를 수신하여 모니터하고, 특이사항 검출 및 이에 대한 대응 프로세스를 갖추는 등의 고도의 기능을 구비한 중앙 집중형 감시 시스템으로 주로 비즈니스 영역에서 구축되어지고 서비스 되어지는 시스템이다[1]-[3].

중앙 집중형 감시 시스템은 넓은 지역에 걸쳐 다수의 감시 카메라를 설치하고 이들을 사설 네트워크로 연결하는 경우가 가능하다. 이러한 경우 트래픽 수용 및 전달 지연 측면에서 양질의 감시 서비스를 제공할 수는 있으나, 비용적으로 비효율적인 경우가 많아, 특수한 환경이나 요구가 있는 경우에 가능하다. 최근에는 인터넷 등 양질의 공중 네트워크가 우리 사회 전반에 폭넓게 보급되어 언제 어디서나 전달 서비스를 이용할 수 있다. 이러한 환경에서 감시 카메라 네트워크를 공중 네트워크 기반으로 구축하는 것은 빠른 구축 시간과 시스템 구성의 용이한 변경 및 비용적인 측면에서 효율적이다[4].

일반적으로 감시의 특성상 감시 카메라 시스템은 움직이는 물체나 사물의 이동 등에 따라 해당 부분에 대하여 집중적으로 감시하는 경우가 많다. 이에 따라 최근의 감시 카메라는 PTZ 기능이 구현되어 있어 움직임이 없을 때에는 프레임을 생성하지 않고 있다가 움직임이 포착되는 경우 물체 방향으로 회전 및 확대하여 관심 있는 부분에 대한 화상 프레임을 만들어 전송하는 지능형 기능을 수행한다. 그러므로 감시 카메라 네트워크 시스템에 설치되어 있는 많은 감시 카메라는 감시 영역 내의 움직임 유무에 따라 프레임을 만들어 전송하거나, 그렇지 않은 경우 프레임 전송 측면에서 유휴한 상태를 유지한다[5].

규모가 큰 감시 카메라 시스템은 설치되어 운영하는 카메라의 개수가 수십~수백 개 또는 수천 개까지 가능하다. 이런 경우 수많은 카메라로부터 전달되어 오는 모든 화상 프레임을 사람이 일일이 실시간으로 모니터링하는 것이 현실적으로 어려운 상황이다. 또 어떤 경우에는 사람이나 관심 동물의 유무에 관계없는 일반적인 움직임, 즉 바람에 날리는 낙엽 등에 따라 생성되어 전송되어 오는 화상 프레임의 경우는 중앙 감시 센터에서는 전혀 관심이 없는, 무시해도 되는 화상 정보이다.

이에 대한 보완 방법으로 전달되어 오는 화상 프레임에 관심 대상인 사람이나 동물 등이 있는지 여부에 따라 선별적으로 화상을 분류할 수 있는 화상 인식 시스템을 설치한다면 실시간 모니터링을 보다 효과적으로 수행할 수 있게 된다. 특히 사람의 얼굴을 인식하여 처리하는 화상 인식 시스템의 경우 사람의 유무 여부를 판단하는 기능 이외에도 여러 관심 인물들의 얼굴 정보를 모아놓은 데이터베이스와 연동하여 특정 인물이 화상 안에 있는 지의 여부에 대한 서비스를 제공할 수 있다. 이러한 서비스는 수동적인 화상 모니터링의 기능을 넘어서는 사람에 대한 아이덴터티 확인 기능이 있는 유용한 기능으로서 최근 활용도가 높아져 가는 서비스이다. 이러한 서비스가 같이 결합되어 구현되는 경우 수많은 감시 카메라로부터 오는 화상 프레임에 대하여 화상 인식 시스템이 화상 프레임내의 사람이 관심 인물 등과 매치되었을 경우 실시간적으로 알람 등으로 통지하게 됨으로써 모든 화상 프레임에 대하여 일일이 사람의 눈으로 확인하는 절차를 대신하게 된다.

그러나 화상 인식 시스템이 설치되어 운영되는 경우 도착하는 화상 프레임의 수가 너무 많으면 화상 인식을 위해 입력 큐에 대기하는 시간을 길어지는 경우가 발생할 수 있다. 이 경우 화상 인식이 너무 늦어지면 감시 카메라 시스템의 실시간성의 요구사항을 만족하지 못할 수 있다. 이와 같은 지연은 화상 인식 시스템의 입력 큐에서뿐만 아니라 화상 카메라로부터 중앙 감시 시스템까지의 화상 프레임의 전달 지연 시간도 영향을 미친다.

화상 프레임의 실시간성을 가능한 한 보장하기 위해서는 위의 두 가지 지연 요소에 대한 최적화가 필요하다. 그러나 많은 경우 네트워크 전달 시간의 최적화는 이미 네트워크가 구성된 이후 또는 일반적인 인터넷 등의 best-effort 특성의 공중 네트워크를 사용하는 경우에는 현실적으로 가능하지 않게 된다. 따라서 본 연구에서는 네트워크를 통한 전달 지연이 있다는 전제하에, 화상 프레임의 실시간성을 보장하기 위한 제어 방법으로 화상 인식 시스템의 입력 큐에서의 지연에 대하여 연구한다. 화상 인식 시스템의 입력 큐에서의 지연을 줄이기 위하여서는 도착하는 화상 프레임의 수를 줄이면 된다. 이 경우 설치된 감시 카메라의 수를 줄이는 경우가 된다. 만약 감시 카메라의 수를 늘리면 감시 카메라로부터 발생되어 전달되어 오는 화상 프레임의 수가 더불어 많아지므로 화상 인식 시스템의 입력 큐에서의 지연이 커지게 되어 실시간성 요건을 위반할 가능성이 높아진다. 그러므로 실시간성 처리와 설치되어 운영되는 카메라의 수는 상호 보완 관계에 있게 된다.

이에 본 연구에서는 다수의 감시 카메라가 네트워크를 통하여 연결되어 있고, 화상 인식 시스템이 구축되어있는 실시간 중앙 집중형 감시 시스템을 고려한다. 그리고 감시 카메라로부터 오는 화상 프레임의 처리에 대한 실시간성을 보장하기 위한 네트워크 전달 시간 및 화상 인식 시스템의 입력 큐에서의 지연을 분석한다. 분석에서 서버에서의 화상 프레임 처리시간은 일반적인 분포를 갖는다고 가정한다. 다음으로 실시간성 위반 비율과 감시 카메라 수의 관계를 분석함으로써, 실시간성 보장을 위한 최적의 카메라 수에 대한 설계 기준을 제시한다.

Ⅱ. 관련연구

감시 카메라 네트워크 시스템의 성능에 대한 연구는 대부분 화상 인식의 정확성, 화상 프레임의 전송 품질, 전송 프레임 수, 네트워크의 대역폭, 그리고 전송 데이터의 보안 기능에 대한 내용이 주로 연구되어 왔다.

[6]에서는 폐쇄회로텔레비전 시스템에서 네트워크 대역폭과 제한된 처리자원을 기준으로 어떤 카메라의 화상 데이터를 우선적으로 저장할 지에 대한 효과적인 스케줄링 방법에 대한 연구를 수행하였다. 그리고 제안한 스케줄링에서 연속 화상 프레임 간 지터 최소화를 위한 연구를 진행하였다. 또한 [7]에서는 비디오 분석 기반 감시에 필요한 효과적인 프레임 수에 대한 연구를 수행되었다. 이 연구에서는 특이 상황에서의 전송 프레임 수는 초당 8 프레임 정도면 충분하다고 보았으며, 일반적인 상황에서는 훨씬 적은 프레임도 가능하다고 하였다. 또한 프레임 수뿐만 아니라 이미지 해상도, 압축 방법도 비디오 분석에 영향을 미친다고 주장하였다. [8]에서는 사용자와 서버가 연동하여 HTTP 상에서 동적 방법 기반 스트리밍 제공 방식을 제시하였는데, 이 방식에서는 사용자에게 현재 채널의 자원 정보를 제공함으로써 이어지는 세그먼트의 해상도 등을 결정할 수 있도록 하였다.

[4]에서는 감시 시스템이 5G 이동통신망에 연결되어 다른 일반 트래픽과 통신망을 공유하여 전송될 때, 비디오 세그먼트의 화질과 크기에 대한 동적 선택 알고리즘 연구를 수행하였다. 이 논문에서는 카메라와 네트워크 트래픽 정도에 기반하여 가용 대역폭을 평가하고 다음에 보낼 화상 프레임의 사이즈를 결정하는 연구를 수행하였다. [2]에서는 네트워크 기반의 지능형 분산 감시 시스템의 응용에 관한 기능을 연구하였으며, 특정 적용 분야로써 공항 등과 같은 공공장소에서 효과적이고 안전한 환경을 만들 수 있는 지능화된 인식 시스템을 연구하였다. [9]에서는 폐쇄회로텔레비전의 화상 이미지에 관한 여러 가지 안면 인식 알고리즘의 평가 연구를 수행하였으며, [10]에서는 감시 카메라 시스템의 보안 기능 측면에 관하여 연구하였다. [5]에서는 감시 카메라의 인식 상태와 유휴 상태간의 전이특성을 기반으로한 화상 인식 서버의 활용도 및 프레임 폐기율에 기반한 감시 시스템의 최적 구성에 대한 연구를 수행하였다.

폐쇄회로텔레비전 기반의 감시 카메라 시스템은 사회 안전 및 작업장에서의 안전사고 예방을 위한 스마트 안전관리 시스템에도 활용된다. [3]에서는 안전사고 예방을 위하여 인공지능 화상 인식을 기반으로 작업장 환경을 24시간 감시할 수 있는 자동화 안전 감시 시스템 및 특이 상황 발생시에 이를 자동적으로 알릴 수 있는 위험 감지 시스템을 제안 설계하였다. [1]에서는 사용자의 응급 상황이나 안전한 귀가를 목적으로 하는 안심 귀가 시스템에서 PTZ(Pan Tilt Zoom) 폐쇄회로텔레비전 및 고정 카메라를 이용하여 스마트 관제 서비스의 서비스율을 개선하였다.

[11]의 연구에서는 폐쇄회로텔레비전 시스템의 안면 인식에서 발생할 수 있는 프라이버시에 관한 연구를 수행하였고, 또한 프라이버시 침해 방지 프레임워크를 제안하였다. 그리고 [12]에서는 감시 시스템의 네트워킹 및 시각화와 경계 지역 보안 등을 사용한 적응형 알고리즘 기반 보안 기능 향상 방법을 연구하였다.

위와 같은 많은 연구에도 불구하고 본 논문에서 다루고자 하는 중앙집중형 감시 시스템에서의 실시간성을 제공하기 위한 지연 분석 및 그에 따른 수용 가능한 트래픽과 카메라 수의 최적 구성에 관한 연구는 거의 수행되지 않은 상태이다.

Ⅲ. 분석 모델

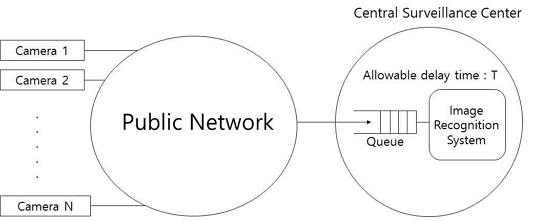
본 논문에서 고려하는 허용 지연 시간을 갖는 중앙 집중형 감시 카메라 시스템을 그림 1에 나타내었다. 그림 1의 감시 카메라 시스템 동작 과정은 다음과 같다. N개의 화상 카메라가 네트워크를 통과하여 중앙 감시 센터에 연결되어 있다. 각 화상 카메라는 화상 프레임이 생성될 경우 네트워크를 통하여 중앙 감시 센터로 전송한다. 화상 카메라 i (1≤i≤N)는 평균적으로 단위 시간당 λ_i개의 화상 프레임을 발생한다고 가정한다. 네트워크의 전달시간은 프레임 간 독립적이라고 가정하며, 확률밀도함수가 f_a(t)인 랜덤 변수 (random variable) a로 표시한다. 또한 a의 평균값을 $$ \overline{a}$$라고 표시한다. 중앙 감시 센터로 전달된 화상 프레임은 화상 인식 시스템의 처리를 위한 입력 큐에 들어간다. 각 화상 프레임에 대한 화상 인식 시스템의 처리 시간은 프레임 간 독립적이라고 가정하며, 확률밀도함수가 f_c(t)인 랜덤 변수 c로 표시한다. 마찬가지로 c의 평균값을 $$ \overline{c}$$라고 표시한다. N개의 화상 카메라로부터 전송되어 화상 인식 시스템의 입력 큐에 도착하는 화상 프레임의 도착 패턴은 $$ \lambda =\sum _{i=1}^N{\lambda }_i$$의 도착률을 갖는 포아슨 분포를 따른다고 가정한다. 이는 독립적으로 발생하는 트래픽인 경우 발생 형태가 어떤 형태라도 발생 소스가 많은 경우에는 그 합은 포아슨 분포에 따르게 되는 특성에 기인함으로, 본 연구에서 가정하고 있는 N>>1 인 경우에 대하여서는 현실적으로 적용 가능한 타당한 가정이다. 포아슨 분포의 도착률로부터 개별 화상 프레임의 도착 시간 간격은 메모리리스 특성을 갖게 된다. 본 연구에서는 이러한 N>>1 인 경우에 여러 위치에서 독립적으로 발생하는 화상 프레임의 메모리리스 특성으로부터 트래픽이 네트워크를 통하여 중앙 감시 센터에 도달할 때까지의 전달시간 a에 대하여 지수분포를 갖는다고 가정한다. 화상 프레임이 화상 인식 시스템의 입력 큐에서의 대기 시간을 확률밀도함수가 f_b(t)인 랜덤 변수 b로 표시하며, 평균값은 $$ \overline{b}$$라고 나타낸다. 위의 가정으로부터 화상 프레임이 화상 카메라로부터 출발하여 화상 인식 시스템의 처리가 끝날 때까지 거치는 시간 d는 아래의 식과 같이 구해진다.

Fig. 1.

Analysis model of central surveillance camera system

d의 확률 밀도 함수는 f_d(t)로 나타내며 평균값은 $$ \overline{d}$$로 표시한다. 화상 프레임의 허용 지연 시간으로써 실시간성 기준 T를 가정한다. 즉 d > T의 지연을 갖는 화상 프레임은 실시간성을 만족하지 못한 프레임으로 간주한다. 그리고 전체 화상 프레임 대비 실시간성을 만족하지 못하는 화상 프레임의 비율을 실시간성 위반 비율 E라고 표시한다. 실시간성 위반 비율 E은 다음과 같이 구해진다.

화상 인식 서버의 입력 큐에서의 지연인 랜덤 변수 b에 대한 분포는 M/G/1 대기이론 모델을 적용함으로서 구할 수 있다. f_b(t) 및 f_c(t)에 대한 라플라스 변환을 각각 B^*(s), C^*(s)라고 하고, 서버의 가동률을 $$ \rho =\lambda \cdot \overline{c}$$로 정의할 때 [13]으로부터 다음의 관계식을 얻을 수 있다.

f_d(t) 및 f_a(t)에 대한 라플라스 변환을 각각 D^*(s), A^*(s)라고 할 때 식 (1)의 관계로부터 다음의 식을 얻을 수 있다.

위의 식의 D^*(s)로부터 f_d(t)를 구할 수 있으며, 식 (2)를 통하여 E을 구할 수 있다.

본 연구에서는 서버의 화상 프레임 처리시간이 일반적인 분포를 갖는다고 가정한다. 일반적인 분포의 경우 다양한 형태로 주어질 수 있으나, 본 연구에서는 가장 널리 사용되는 Erlangian 분포와 hyperexponential 분포에 대하여 결과를 분석한다. 이는 실제 환경에서의 분포가 정확히 수식의 형태로 주어지지 않는 경우가 대부분인데, 그 때 주어진 분포를 수식의 형태로 근사화하여 분석을 진행함으로써 유효한 결과를 얻을 수 있으며, 이러한 근사화는 주어진 분포의 변동계수(coefficient of variation)가 1보다 작을 때 Erlangian 분포로, 주어진 분포의 변동계수가 1보다 큰 경우에는 hyperexponential 분포로 근사화가 가능하기 때문이다. 또한 Erlangian분포와 hyperexponential 분포의 특수한 경우에 해당되는 지수분포의 경우에 대하여서도 결과 분석을 추가한다. 지수분포는 변동계수가 1인 경우에 해당한다.

3-1 Erlangian 분포의 화상 프레임 처리시간

화상 프레임 처리시간이 r-stage Erlangian 분포를 갖는 경우, $$ \mu =\frac{1}{\overline{c}}$$라고 할 때 f_c(t)와 C^*(s)는 다음과 같이 주어지며,

$\[ \begin{array}{cc}{f}_c\left(t\right)=\frac{r\mu {\left(r\mu t\right)}^{r-1}}{\left(r-1\right)!}{e}^{-r\mu t}\hfill & \left(t\ge 0\right)\hfill \end{array} \]$

(5)

$\[ C^{\mathrm{*}}\left(s\right)={\left(\frac{r\mu }{s+r\mu }\right)}^r, \]$

(6)

(3) 식으로부터 B^*(s)를 다음과 같이 구할 수 있다.

$\[ B^{\mathrm{*}}\left(s\right)=\frac{s\left(1-\rho \right)}{s-\lambda +\lambda {\left(\frac{r\mu }{s+r\mu }\right)}^r} \]$

(7)

랜덤 변수 a는 지수분포를 가지므로 다음의 식이 성립한다.

$\[ \begin{array}{cc}{f}_a\left(t\right)=\frac{1}{\overline{a}}{e}^{-\frac{1}{\overline{a}}t}\hfill & \left(\mathrm{t}\ge 0\right),\hfill \end{array} \]$

(8)

$\[ A^{\mathrm{*}}\left(s\right)=\frac{1}{\overline{a}s+1} \]$

(9)

따라서 D^*(s)는 다음과 같이 주어진다.

$\[ \begin{array}{c}{D}^{\mathrm{*}}\left(s\right)=A^{\mathrm{*}}\left(s\right)B^{\mathrm{*}}\left(s\right)C^{\mathrm{*}}\left(s\right)\hfill \\ =\frac{1}{\overline{a}s+1}\cdot \frac{s(1-\rho )}{s-\lambda +\lambda {\left(\frac{r\mu }{s+r\mu }\right)}^r}\cdot {\left(\frac{r\mu }{s+r\mu }\right)}^r\hfill \end{array} \]$

(10)

식 (10)은 r의 값이 주어지면 분모가 1차식인 부분분수로 표현이 가능하고, 이를 라플라스 역변환을 수행함으로써 f_d(t)를 구할 수 있으며, 이어 식 (2)에 의하여 E를 구할 수 있다.

r은 다양한 값을 갖을 수 있으나, 본 절에서는 하나의 경우로서 r=2일 때에 대하여 다음과 같이 수식 분석을 진행한다. r이 다른 값을 갖는 경우에도 같은 절차를 적용하여 구할 수 있다.

$\[ D^{\mathrm{*}}\left(s\right)\begin{array}{l}=\frac{1}{\overline{a}s+1}\cdot \frac{s\left(1-\rho \right)}{s-\lambda +\lambda {\left(\frac{2\mu }{s+2\mu }\right)}^2}\cdot {\left(\frac{2\mu }{s+2\mu }\right)}^2\hfill \\ =\frac{1}{\overline{a}s+1}\cdot \frac{4{\mu }^2\left(1-\rho \right)}{s^2+\left(4\mu -\lambda \right)s+4\mu \left(\mu -\lambda \right)}\hfill \\ =\frac{1}{\overline{a}s+1}\cdot \frac{4{\mu }^2\left(1-\rho \right)}{s^2+\mu \left(4-\rho \right)s+4{\mu }^2\left(1-\rho \right)}\hfill \\ =\frac{4{\mu }^2\left(1-\rho \right)}{\overline{a}}\cdot \frac{1}{s+\frac{1}{\overline{a}}}\cdot \frac{1}{s^2+\mu \left(4-\rho \right)s+4{\mu }^2\left(1-\rho \right)}\hfill \\ =\frac{4{\mu }^2\left(1-\rho \right)}{\overline{a}}\cdot \frac{1}{s+\frac{1}{\overline{a}}}\cdot \frac{1}{\left(s+{\alpha }_1\right)\left(s+{\alpha }_2\right)}\hfill \end{array} \]$

(11)

단 윗 식에서 $$ {\alpha }_1=\frac{\mu }{2}\left(4-\rho +\sqrt{{\rho }^2+8\rho }\right)$$, $$ {\alpha }_2=\frac{\mu }{2}\left(4-\rho -\sqrt{{\rho }^2+8\rho }\right)$$ 이다.

D^*(s)는 다음과 같이 부분분수 형태로 변환할 수 있다.

$\[ D^{*}\left(s\right)=\frac{4{\mu }^2\left(1-\rho \right)}{\overline{a}}\cdot \left(\frac{A_0}{s+\frac{1}{\overline{a}}}+\frac{A_1}{s+{\alpha }_1}+\frac{A_2}{s+{\alpha }_2}\right) \]$

(12)

단 윗 식에서 $$ A_0=\frac{1}{\left({\alpha }_1-\frac{1}{\overline{a}}\right)\left({\alpha }_2-\frac{1}{\overline{a}}\right)}$$, $$ A_1=\frac{1}{\left({\alpha }_1-\frac{1}{\overline{a}}\right)\left({\alpha }_1-{\alpha }_2\right)}$$, $$ A_2=\frac{-1}{\left({\alpha }_2-\frac{1}{\overline{a}}\right)\left({\alpha }_1-{\alpha }_2\right)}$$ 이다.

따라서 f_d(t)를 구할 수 있다.

$\[ \begin{array}{cc}{f}_d\left(t\right)=\frac{4{\mu }^2\left(1-\rho \right)}{\overline{a}}\cdot \left(A_0{e}^{-\frac{t}{\overline{a}}}+A_1{e}^{-{\alpha }_{1}t}+A_2{e}^{-{\alpha }_{2}t}\right)\hfill & \left(t\ge 0\right)\hfill \end{array} \]$

(13)

(2)식으로부터 E는 다음과 같이 주어진다.

$\[ E=\frac{4{\mu }^2\left(1-\rho \right)}{\overline{a}}\cdot \left(\overline{a}{A}_0{e}^{-\frac{T}{\overline{a}}}+\frac{A_1}{{\alpha }_1}{e}^{-{\alpha }_{1}T}+\frac{A_2}{{\alpha }_2}{e}^{-{\alpha }_{2}T}\right) \]$

(14)

그림 2는 감시 카메라 시스템이 $$ \overline{a}$$ = 0.1의 지수분포 네트워크 전달시간 및 $$ \overline{c}$$ = 0.01의 Erlangian 분포의 프레임 처리시간을 가질 때 T=400ms, 600ms, 800ms, 1000ms인 경우에 프레임 도착률에 따른 E의 변화를 나타낸다. $$ \overline{c}$$=0.01인 경우 화상 인식 시스템의 평균적인 프레임 처리시간은 10ms로서 초당 평균 100개의 화상 프레임 처리용량을 나타내며, $$ \overline{a}$$=0.1은 프레임의 네트워크 전달시간이 평균적으로 100ms임을 나타낸다. 허용 지연 시간으로써의 실시간 판단 기준인 T값이 400ms인 경우는 민감한 경우로 극도의 실시간성을 요구하는 경우이며, 반면 T값이 1000ms인 경우는 1초간의 지연이 있는 경우로서 시간에 아주 민감한 분야가 아니면 현실적으로 적용 가능한 값이 된다. 그림 2에서 볼 수 있듯이 T=400ms일 때 도착률에 따른 실시간성 위반 비율 E이 가장 높으며, 반면 T가 커질수록 E가 작게 관찰되는 것을 알 수 있다. 이는 실시간성 기준을 엄격하게(작게) 설정하면 이를 위반하여 도착하는 프레임 비율이 커지게 되는 상식에 기인한다.

Fig. 2.

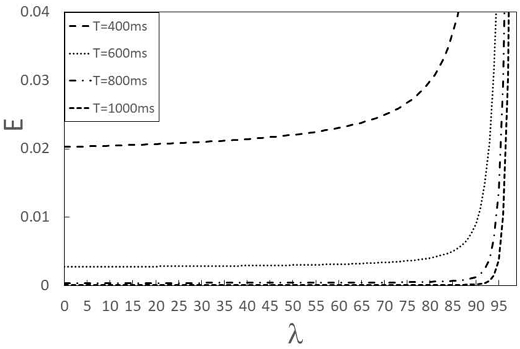
E according to allowable delay time and frame arrival rate in the case of frame processing time with Erlangian distribution (a¯=0.1, c¯=0.01 and T=400ms, 600ms, 800ms, 1000ms)

화상 감시 시스템을 설계할 때 적용 도메인에 따라 실시간성에 기반하여 위반 비율을 어느 정도로 유지할 지 결정하게된다. 위반 비율에 따라 수용 가능한 총 도착률을 결정하고, 이를 기준으로 최대 수용 가능한 화상 카메라의 수를 정하게 된다. 표 1에 T=200ms, 400ms, 600ms, 800ms, 1000ms이고, E=1%, 5%, 20%일 때의 수용 가능한 총 도착률 및 이를 기반으로한 수용 가능 화상 카메라의 수를 나타내었다. 화상 카메라 수 계산 시에 수식의 편의상 모든 화상 카메라의 프레임 발생 비율이 평균적으로 초당 0.5 ($$ {\lambda }_i=\frac{\lambda }{N}=0.5$$, 1≤i≤N)라고 가정하였다. 만약 λ_i가 i에 따라 달라지는 경우에는도출된 총 도착률 λ에 대하여 $$ \lambda =\sum _{i=1}^{N^{\text{'}}}{\lambda }_i$$인 N^'로서 화상 카메라의 수를 구하면 된다.

Table 1.

Number of cameras that can be accommodated when Erlangian frame processing time and E=1%, 5%, 20% (a¯=0.1, c¯=0.01, λi=0.5)

표 1에서 네트워크를 통한 전달 지연 a가 200ms이상의 값을 갖을 확률이 15%이고, 400ms 이상의 값을 갖을 확률이 2%이므로 E=1%인 경우의 해당 값을 불가로 표시하였다. 마찬가지로 E=5%인 경우에 200ms의 경우에도 불가로 표시하였다. E=1%인 경우에 T=600ms일 때 수용가능한 화상 카메라 수는 180대이며, T=800ms일 때 188대, T=1000ms로 변경할 경우 190대까지 증가함을 알 수 있다. E=20%로 크게 변경하는 경우 T=200ms, 400ms를 제외한 다른 3경우에 모두 194대 이상이 가능함으로써 설치 가능한 최대 카메라 수가 200대에 근접함을 알 수 있다.

3-2 Hyperexponential 분포의 화상 프레임 처리시간

화상 프레임 처리시간이 R-phase hyperexponential 분포를 갖는 경우, f_c(t)와 C^*(s)는 다음과 같이 주어진다.

$\[ \begin{array}{ccc}{f}_c\left(t\right)=\sum _{i=1}^R{h}_i{\mu }_i{e}^{-{\mu }_{i}t}\hfill & \left(t\ge 0\right),\hfill & \text{단} \overline{c}=\sum _{i=1}^R\frac{h_i}{{\mu }_i}, \sum _{i=1}^R{h}_i=1\hfill \end{array} \]$

(15)

$\[ C\mathrm{*}\left(s\right)=\sum _{i=1}^R{h}_i\frac{{\mu }_i}{s+{\mu }_i}, \]$

(16)

식 (3)으로부터 B^*(s)를 다음과 같이 구할 수 있다.

$\[ B^{\mathrm{*}}\left(s\right)=\frac{s\left(1-\rho \right)}{s-\lambda +\lambda \sum _{i=1}^R{h}_i\frac{{\mu }_i}{s+{\mu }_i}} \]$

(17)

따라서 D^*(s)는 다음과 같이 주어진다.

$\[ \begin{array}{c}{D}^{\mathrm{*}}\left(s\right)=A^{\mathrm{*}}\left(s\right)B^{\mathrm{*}}\left(s\right)C^{\mathrm{*}}\left(s\right)\hfill \\ =\frac{1}{\overline{a}s+1}\cdot \frac{s\left(1-\rho \right)}{s-\lambda +\lambda \sum _{i=1}^R{h}_i\frac{{\mu }_i}{s+{\mu }_i}}\cdot \sum _{i=1}^R{h}_i\frac{{\mu }_i}{s+{\mu }_i}\hfill \end{array} \]$

(18)

식 (18)은 R의 값이 주어지면 분모가 1차식인 부분분수로 표현이 가능하고, 이를 라플라스 역변환을 수행함으로써 f_d(t)를 구할 수 있으며, 이어 식 (2)에 의하여 E를 구할 수 있다.

R은 다양한 값을 갖을 수 있으나, 본 절에서는 하나의 경우로서 R=2일 때에 대하여 수식 분석을 진행한다. R이 다른 값을 갖는 경우에도 같은 절차를 적용하여 구할 수 있다. R=2인 경우 다음과 같이 주어진다.

$\[ \begin{array}{c}{D}^{\mathrm{*}}\left(s\right)=\frac{1}{\overline{a}s+1}\cdot \frac{s\left(1-\rho \right)}{s-\lambda +\lambda \sum _{i=1}^2{h}_i\frac{{\mu }_i}{s+{\mu }_i}}\cdot \sum _{i=1}^2{h}_i\frac{{\mu }_i}{s+{\mu }_i}\hfill \\ \begin{array}{cc}\overline{c}=\frac{h_1}{{\mu }_1}+\frac{h_2}{{\mu }_2}=\frac{h_1{\mu }_2+h_2{\mu }_1}{{\mu }_1{\mu }_2}=\frac{\rho }{\lambda },\hfill & h_1+h_2=1\hfill \end{array}\hfill \end{array} \]$

(19)

D^*(s)는 다음과 같이 정리되어진다.

$\[ \begin{array}{l}{D}^{\mathrm{*}}\left(s\right)=\frac{1}{\overline{a}s+1}\cdot \frac{s\left(1-\rho \right)}{s-\lambda +\lambda \sum _{i=1}^2{h}_i\frac{{\mu }_i}{s+{\mu }_i}}\cdot \sum _{i=1}^2{h}_i\frac{{\mu }_i}{s+{\mu }_i}\hfill \\ =\begin{array}{l}\frac{1}{\overline{a}s+1}\cdot \hfill \\ \frac{\left(1-\rho \right)\left(h_1{\mu }_1\left(s+{\mu }_2\right)+h_2{\mu }_2\left(s+{\mu }_1\right)\right)}{s^2+\left({\mu }_1+{\mu }_2-\lambda \right)s+{\mu }_1{\mu }_1-\lambda \left(1-h_1\right){\mu }_1-\lambda \left(1-h_2\right){\mu }_2}\hfill \end{array}\hfill \\ =\frac{1}{\overline{a}s+1}\cdot \frac{\left(1-\rho \right)\left(\left(h_1{\mu }_1+h_2{\mu }_2\right)s+{\mu }_1{\mu }_2\right)}{s^2+\left({\mu }_1+{\mu }_2-\lambda \right)s+{\mu }_1{\mu }_2\left(1-\rho \right)}\hfill \\ =\frac{1-\rho }{\overline{a}}\cdot \frac{1}{s+\frac{1}{\overline{a}}}\cdot \frac{\left(h_1{\mu }_1+h_2{\mu }_2\right)s+{\mu }_1{\mu }_2}{s^2+\left({\mu }_1+{\mu }_2-\lambda \right)s+{\mu }_1{\mu }_2\left(1-\rho \right)}\hfill \\ =\frac{\left(h_1{\mu }_1+h_2{\mu }_2\right)\left(1-\rho \right)}{\overline{a}}\cdot \frac{1}{s+\frac{1}{\overline{a}}}\cdot \frac{s+K}{\left(s+{\beta }_1\right)\left(s+{\beta }_2\right)}\hfill \end{array} \]$

(20)

단 윗 식에서 $$ K=\frac{{\mu }_1{\mu }_2}{h_1{\mu }_1+h_2{\mu }_2}$$, $$ {\beta }_1=\frac{{\mu }_1+{\mu }_2-\lambda +\sqrt{{\left({\mu }_1+{\mu }_2-\lambda \right)}^2-4{\mu }_1{\mu }_2\left(1-\rho \right)}}{2}$$, $$ {\beta }_2=\frac{{\mu }_1+{\mu }_2-\lambda -\sqrt{{\left({\mu }_1+{\mu }_2-\lambda \right)}^2-4{\mu }_1{\mu }_2\left(1-\rho \right)}}{2}$$ 이다.

D^*(s)는 다음과 같이 부분분수 형태로 변환할 수 있다.

$\[ D^{\mathrm{*}}\left(s\right)=\frac{\left(h_1{\mu }_1+h_2{\mu }_2\right)\left(1-\rho \right)}{\overline{a}}\cdot \left(\frac{B_0}{s+\frac{1}{\overline{a}}}+\frac{B_1}{s+{\beta }_1}+\frac{B_2}{s+{\beta }_2}\right) \]$

(21)

단 윗 식에서 $$ B_0=\frac{K-\frac{1}{\overline{a}}}{\left({\beta }_1-\frac{1}{\overline{a}}\right)\left({\beta }_2-\frac{1}{\overline{a}}\right)}$$, $$ B_1=\frac{K-{\beta }_1}{\left({\beta }_1-\frac{1}{\overline{a}}\right)\left({\beta }_1-{\beta }_2\right)}$$, $$ B_2=\frac{{\beta }_2-K}{\left({\beta }_2-\frac{1}{\overline{a}}\right)\left({\beta }_1-{\beta }_2\right)}$$이다.

따라서 f_d(t)를 다음과 같이 구할 수 있다.

$\[ \begin{array}{cc}{f}_d\left(t\right)=\frac{\left(h_1{\mu }_1+h_2{\mu }_2\right)\left(1-\rho \right)}{\overline{a}}\cdot \left(B_0{e}^{-\frac{t}{\overline{a}}}+B_1{e}^{-{\beta }_{1}t}+B_2{e}^{-{\beta }_{2}t}\right)\hfill & \left(t\ge 0\right)\hfill \end{array} \]$

(22)

식 (2)로부터 E는 다음과 같이 주어진다.

$\[ E=\frac{\left(h_1{\mu }_1+h_2{\mu }_2\right)\left(1-\rho \right)}{\overline{a}}\cdot \left(\overline{a}{B}_0{e}^{-\frac{T}{\overline{a}}}+\frac{B_1}{{\beta }_1}{e}^{-{\beta }_{1}T}+\frac{B_2}{{\beta }_2}{e}^{-{\beta }_{2}T}\right) \]$

(23)

그림 3은 감시 카메라 시스템이 $$ \overline{a}$$ = 0.1의 지수분포 네트워크 전달시간 및 $$ \frac{1}{{\mu }_1}$$=0.015, $$ \frac{1}{{\mu }_2}$$=0.005, h₁ = h₂ = 0.5, 즉 $$ \overline{c}$$ = 0.01인 2-phase hyperexponential 분포의 프레임 처리시간을 갖을 때 T=400ms, 600ms, 800ms, 1000ms인 경우에 프레임 도착률에 따른 E의 변화를 나타낸다. $$ \frac{1}{{\mu }_1}$$=0.015, $$ \frac{1}{{\mu }_2}$$=0.005, h₁ = h₂ = 0.5, 즉 $$ \overline{c}$$ = 0.01인 값을 갖는 2-phase hyperexponential 분포는 3-1 절의 $$ \overline{c}$$ = 0.01의 Erlangian 분포와 화상 프레임의 처리시간 평균은 같으나 변동 계수가 1보다 큰 값을 갖는 경우이다. 변동 계수가 크다는 것은 화상 인식 시스템의 입력 큐에서의 대기 시간의 변동 폭이 크다는 것을 의미하며, 이는 화상 프레임의 실시간성 위반 비율이 높아짐을 의미한다. 그림 2의 그래프와 비교하여, 그림 3의 그래프에서는 T=400ms, 600ms, 800ms, 1000ms의 모든 경우에 대하여 E 값이 더 높게 형성됨을 확인할 수 있다. 그림 2와 마찬가지로 그림 3에서도 T=400ms일 때 도착률에 따른 실시간성 위반 비율 E이 가장 높으며, 반면 T가 커질수록 E가 작게 관찰되는 것을 알 수 있다. 이는 실시간성 기준이 엄격해짐에 따라 이를 위반하여 도착하는 프레임 비율이 커지게 됨을 다시 한번 확인할 수 있다.

Fig. 3.

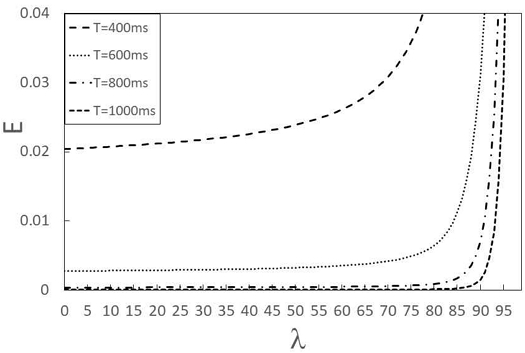
E according to allowable delay time and frame arrival rate in the case of frame processing time with 2-phase hyperexponential distribution (a¯=0.1, 1μ1=0.015, 1μ2= 0.005, h1 = h2 = 0.5 (c¯=0.01) and T=400ms, 600ms, 800ms, 1000ms)

표 2에 T=200ms, 400ms, 600ms, 800ms, 1000ms이고, E=1%, 5%, 20%일 때의 수용 가능한 총 도착률 및 이를 기반으로한 수용 가능 화상 카메라 수를 나타내었다. 화상 카메라 수 계산 시에 3-1절과 마찬가지로 모든 화상 카메라의 프레임 발생 비율이 평균적으로 초당 0.5 ($$ {\lambda }_i=\frac{\lambda }{N}=0.5$$, 1≤i≤N)라고 가정하였다. 네트워크를 통한 전달 지연 a가 200ms이상의 값을 갖을 확률이 15%이고, 400ms 이상의 값을 갖을 확률이 2%이므로 표 1과 마찬가지로 표 2에서도 E=1%인 경우의 해당 값을 불가로 표시하였다. 마찬가지로 E=5%인 경우에 200ms의 경우에도 불가로 표시하였다. E=1%인 경우 수용가능한 화상 카메라 수는 T=600ms일 때 168대이며, T=800ms일 때 180대, T=1000ms일때 186대로, 표 1에서의 각각 180대, 188대, 190대에 비하여 줄어들었음을 알 수 있다. 이는 hyperexponential 분포의 변동 계수가 Erlangian 분포의 변동 계수보다 크므로 나타나는 현상이다. 따라서 화상 프레임의 처리시간에 대한 변동 계수가 큰 경우에는 수용가능한 카메라 수를 상대적으로 보수적으로 잡아 운영할 필요가 있다. E=20%로 크게 변경하는 경우 T=200ms, 400ms를 제외한 다른 3경우에 모두 190대 이상의 값을 갖게 된다.

Table 2.

Number of cameras that can be accommodated when 2-phase hyperexponential frame processing time and E=1%, 5%, 20% (a¯=0.1, 1μ1=0.015, 1μ2= 0.005, h1 = h2 = 0.5 (c¯=0.01), λi = 0.5)

3-3 지수 분포의 화상 프레임 처리시간

지수 분포는 Erlangian분포와 hyperexponential 분포의 특수한 경우에 해당되는 분포로서 변동계수가 1인 경우에 해당한다. 3-1절의 r=1인 경우와 3-2절에서 R=1인 경우이므로 중간 과정 없이 실시간성 위반 비율 E의 결과만 제시하면 다음과 같다.

$\[ E=\frac{1-\rho }{\overline{a}\left(1-\rho \right)-\overline{c}}\cdot \left[\overline{a}{e}^{-\frac{T}{\overline{a}}}-\frac{\overline{c}}{1-\rho }{e}^{-\frac{\left(1-\rho \right)T}{\overline{c}}}\right] \]$

(24)

3-1절의 결과 및 3-2절의 결과와 공정한 비교를 위하여 본 절에서도 $$ \overline{c}$$=0.01인 경우를 가정한다. 지수분포의 변동계수는 1로서 변동계수가 1보다 큰 hyperexponential 분포와 1보다 작은 Erlangian 분포의 중간에 위치한다. 따라서 허용 지연 시간 및 프레임 도착률에 따른 E의 그래프도 그림 2와 그림 3의 중간에 위치한다. 이를 확인하기 위하여 표 3에 지수 분포의 경우 T=200ms, 400ms, 600ms, 800ms, 1000ms이고, E=1%, 5%, 20%일 때의 수용 가능한 총 도착률 및 이를 기반으로 수용 가능 화상 카메라 수를 나타내었다. 화상 카메라 수 계산 시에 3-1절, 3-2절과 마찬가지로 모든 화상 카메라의 프레임 발생 비율이 평균적으로 초당 0.5 ($$ {\lambda }_i=\frac{\lambda }{N}=0.5$$, 1≤i≤N)라고 가정하였다. 표 3에서 E=1%인 경우 수용가능한 화상 카메라 수는 T=600ms일 때 174대, T=800ms일 때 184대, T=1000ms일때 188대로 표 2에서의 각각 168대, 180대, 186대 및 표 1에서의 각각 180대, 188대, 190대에 비하여 중간에 위치함을 알 수 있다. 이는 지수 분포의 변동계수가 hyperexponential 분포 및 Erlangian 분포의 변동 계수 사이에 있으므로 나타나는 현상임을 확인할 수 있다.

Table 3.

Number of cameras that can be accommodated when exponential frame processing time and E=1%, 5%, 20% (a¯=0.1, c¯=0.01, λi = 0.5)

Ⅳ. 결 론

본 연구에서는 다수의 감시 카메라가 네트워크를 통하여 화상 인식 시스템에 연결된 실시간 중앙 집중형 감시 시스템을 설계할 때의 기반이 되는 주요 성능 요소들간의 관계를 분석하였다. 성능 요소들로 감시 카메라 네트워크에서 화상 인식 서버의 처리 용량과 설치 가능한 화상 카메라의 대수 그리고 화상 인식 서버의 활용도와 서버에서 처리되지 않고 폐기되는 프레임 수들이 고려되었으며, 이 요소들을 기반으로, 화상 프레임의 처리에 대한 실시간성을 보장하기 위한 네트워크 전달 시간 및 화상 인식 시스템의 입력 큐에서의 지연을 분석하였다. 분석에서 서버의 화상 프레임 처리시간은 일반적인 분포를 갖는다고 가정하였으며, 수식 전개에서는 가장 널리 사용되는 Erlangian 분포와 hyperexponential 분포를 사용하였고, Erlangian 분포와 hyperexponential 분포의 특수한 경우에 해당되는 지수 분포에 대하여서도 결과 분석을 추가하였다. 이어 실시간성 위반 비율과 감시 카메라 수의 관계를 분석함으로써, 실시간성 보장을 위한 최적의 카메라 수에 대한 설계 기준을 제시하였다.

이러한 본 연구에서의 분석 결과는 설치되어 운영될 실시간 화상 감시 카메라 서비스 영역에서 여러 비용 요소를 기반으로 최적의 설계 파라미터를 구할 수 있도록 하는 기반 이론을 제공함으로써, 최근 광범위하게 보급되고, 또한 진화되고 있는 화상 감시 카메라 네트워크의 효율적인 운영을 위하여 크게 유용하게 활용될 것으로 판단된다.

Acknowledgments

이 논문은 2022년도 강원대학교 대학회계의 지원을 받아 수행한 연구임.

References

• D. S. Seong, “Improvement of Service Rate in Smart Surveillance Service using Fixed Camera,” The Journal of Digital Contents Society, Vol. 22, No. 5, pp. 847-853, May 2021. [https://doi.org/10.9728/dcs.2021.22.5.847]
• M. Shah and R. Garrad, “The development of large scale network-based multi-use CCTV surveillance systems,” in Proc. of IEE Int. Symp. on Imaging for Crime Detection and Prevention, pp. 15-22, June 2005. [https://doi.org/10.1049/ic:20050063]
• J. H. Eom, “An Architecture of a Smart Safety Management System to prevent safety Accidents in Workplace,” The Journal of Digital Contents Society, Vol. 21, No. 4, pp. 817-823, April 2020. [https://doi.org/10.9728/dcs.2020.21.4.817]
• E. Khorov, A. Kiryanov, and N. Zhirnov, “SAND- inspired Cross-layer Approach for CCTV in 5G Networks,” in Proceedings of 2017 International Conference on Engineering and Telecommunication (EnT), pp. 33-37, November 2017. [https://doi.org/10.1109/ICEnT.2017.14]
• G. Y. Lee and H. J. Kim, “Optimal Configuration of Surveillance Camera System,” Journal of Korean Institute of Information Technology, Vol. 16, No. 7, pp. 15-25, July 2018. [https://doi.org/10.14801/jkiit.2018.16.7.15]
• K. J. Lin, T. K. Hou, and R. J. Chiu, “Jitter- Constrained Camera Scheduling in CCTV Surveillance Networks,” in Proceedings of 2016 IEEE International Conference on Signal and Image Processing (ICSIP), pp. 650-654, 2016. [https://doi.org/10.1109/SIPROCESS.2016.7888343]
• H. Keval and M. A. Sasse, “to catch a thief – you need at least 8 frames per second: The impact of frame rates on user performance in a CCTV detection task,” in Proceedings of the 16th ACM International Conference on Multimedia, pp. 941-944, October 2008. [https://doi.org/10.1145/1459359.1459527]
• E. Khorov, A. Krasilov, M. Liubogoshchev, and S. Tang, “SEBRA: SAND-enabled bitrate and resource allocation algorithm for network assisted video streaming,” in Proeedings of IEEE 13th International Conference on WiMob, Rome, Italy, pp. 1-8, November 2017. [https://doi.org/10.1109/WiMOB.2017.8115758]
• S. Fahad, S. ur Rahman, I. Khan, and S. Haq, “An Experimental Evaluation of Different Face Recognition Algorithms Using Closed Circuit Television Images,” in Proeedings of 2017 IEEE 2nd International Conference on Signal and Image Processing (ICSIP), pp. 51-54, 2017. [https://doi.org/10.1109/SIPROCESS.2017.8124504]
• S. Yang and J. Park, “An Efficient Access Control Mechanism for Secure Surveillance Systems,” The Journal of Korea Information and Communications Society, Vol. 39B, No. 4, pp. 228-233, April 2014. [https://doi.org/10.7840/kics.2014.39B.4.228]
• B. J. Han, H. Jeong, and Y. J. Won, “The privacy protection framework for biometric information in network based CCTV environment,” in Proceedings of 2011 IEEE Conference on Open Systems, pp. 86-90, September 2011. [https://doi.org/10.1109/ICOS.2011.6079313]
• V. C. Banu, I. M. Costea, F. C. Nemtanu, and I. Bădescu, “Intelligent Video Surveillance System,” in Proeedings of 2017 IEEE 23rd International Symposium for Design and Technology in Electronic Packaging (SIITME), pp. 208-212, 2017. [https://doi.org/10.1109/SIITME.2017.8259891]
• L. Kleinrock, Queueing systems, Vol. 1: Theory, Wiley, 1975.