적응 커널 폭을 가진 최소오차 엔트로피 학습법의 성능 분석
Copyright ⓒ 2023 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
최소오차엔트로피 MEE(minimum error entropy)는 비가우시안 잡음과 다중경로 통신채널 환경에도 우수한 equalization 성능을 지닌다. 그러나 MEE 알고리듬은 두 가지 단점으로 이중 합산의 과중한 계산량 문제와 성능에 민감하게 작용하는 커널 폭 설정 문제가 있다. 오차 전력 평균변화율 접근법을 커널 폭 적응추정에 적용하고 수렴 속도에서 미소한 단점을 보이나 이중합산 없이 계산량을 줄인 Simplified MEE(SMEE) 를 접목하여 낮은 복잡도와 커널 폭의 안정적 적응추정을 제안하였다. 채널 등화 실험 결과는 열악한 잡음환경일수록 SMEE 적응 커널 방식이 안정적으로 수렴하며, 통신 환경에 따라 서로 다른 최적 커널 폭에 수렴하므로 적응 커널 추정이 효과적임을 입증하였다.
Abstract
The minimum error entropy (MEE) algorithm displays superior performance for equalization in multi-path channel environments with non-Gaussian noise. However, there are two major drawbacks consisting of severe computational complexity introduced by the double summation operation and setting the value of kernel width to which performance is very sensitive. In this study, the mean ratio of change of error power for kernel width adaptation is combined with simplified MEE (SMEE) which has no double summation operations but slightly slower convergence compared to MEE. The proposed method has low computational complexity and stable kernel width adaptation. Through experiments on multi-path channel equalization, the proposed SMEE with kernel width adaptation was confirmed to have more stable convergence in severe impulsive noise, and adaptive kernel estimation was found to be effective under different or varying channel characteristics.
Keywords:
MEE, Adaptive kernel width, Error power, Mean ratio of change, Impulsive noise키워드:
적응커널폭, 오차 전력, 평균변화율, 충격성 잡음Ⅰ. 서 론
MSE에 기본을 두고 발전된 모든 신호처리 알고리듬은 충격성 잡음 같은 비가우시안(non-Gaussian) 잡음이 존재하는 환경에서 매우 열악한 성능을 보인다[1]. 이에 오차 샘플의 엔트로피(error entropy)를 최소화하도록 설계된 최소오차엔트로피 MEE(minimum error entropy) 비용함수는 채널의 심각한 심볼간 간섭과 충격성 잡음 환경에서도 우수한 equalization 성능을 지닌다[2]-[4]. 또한 MEE 학습법은 최근 다중 안테나 레이다(MIMO Radar)[5], 전력 시스템 상태추정[6], 우주선 상태추정[7], 머신 러닝[8]-[10]등 가우시안 잡음 하의 신호 및 정보 처리 응용 등에 적극 적용되고 있다. 그러나 MEE는 이중 합산(double summation) 계산이 필요하여 계산량과 복잡도의 문제를 지니고 있다. 이에 MEE의 계산량을 줄여보려는 연구가 이루어졌다. 논문 [11]에서 어느 정도 계산량을 줄였으나 이중합산 과정은 여전히 남아있다. 한편, 논문 [12]에서 성능상의 유의미한 차이가 없으면서 이중 합산을 없앤 간소화된 MEE 기준과 가중치 갱신 알고리듬(이 논문에서 simplified MEE, SMEE라 하겠다)을 제안하였다.
한편, 계산량 문제 외에도 MEE는 고정값 커널 폭이 성능에 매우 민감하게 작용하여 각 통신 환경에 알맞은 커널 폭이 신중하게 선택되어야 한다[13]. 잡음환경이나 채널 왜곡 상태가 바뀌게 되면 입력 신호의 통계적 변화를 추적하여 커널 폭을 적응적으로 조절할 필요가 있다. 이에 논문 [14]에서는 오차샘플들에 확률밀도 추정 최적화 기반의 기존 커널 폭 적응 조절 방법[13]이 MEE에서 적정 커널 폭으로 수렴되지 못함을 밝혔고, 이 문제를 해결하고자 오차 전력의 평균변화율을 활용하여 커널 폭을 갱신하는 새로운 MEE 적응 커널 알고리듬을 제안하였다. 이 적응 커널 폭 알고리듬은 충격성 잡음 환경에서 우수한 수렴 특성을 가지며 초기 커널 폭 선택의 여유도를 크게 향상시킴을 보였다.
여기서, 이 적응적 커널 폭 조절 방법이 간소화된 SMEE 알고리듬에 적용될 수 있다면 계산량 및 복잡도 문제와 커널 폭 설정 문제가 모두 해결될 수 있다. 이 논문에서는 이 적응 커널 폭 방법이 SMEE 알고리듬에 적용될 수 있는지 그리고 어떤 특성들이 나타나는지에 대해 연구하였다.
Ⅱ. MEE와 SMEE 알고리듬
커널 폭 σ의 가우시안 커널 Gσ(•)을 시간 k의 오차에 ek대해 정의하면 다음과 같다.
| (1) |
이 가우시안 커널과 샘플 사이즈 N의 오차 샘플들로 다음과 같이 오차확률밀도를 추정할 수 있다[15],[16].
| (2) |
이 추정 오차확률밀도에 엔트로피를 적용한 Renyi 엔트로피 HR(e)는 다음과 같다[1],[2].
| (3) |
식 (3)의 내항은 다음과 같이 정보 포텐셜(information potential)이 되며 오차 엔트로피를 시스템 가중치 W로 최소화하는 MEE는 정보 포텐셜 V(ek)를 최대화하는 것과 같다[2].
| (4) |
여기서
| (5) |
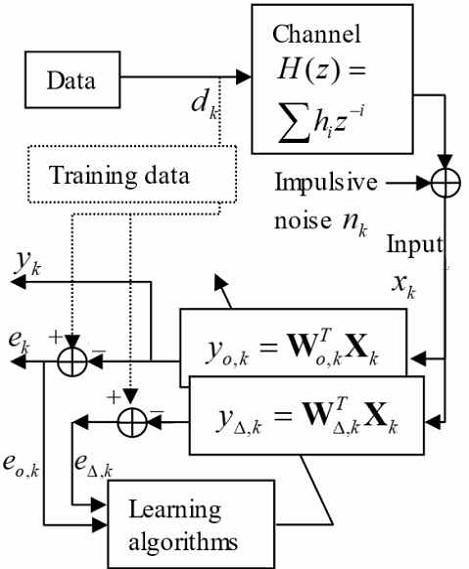
한편, 입력 벡터를 Xk, 출력을 yk라 할 때, L개의 가중치로 구성된 가중치 벡터 Wk의 TDL(tapped delay line)을 시스템으로 하여 입력 벡터 Xk가 들어가면 출력은 가 된다. 원하는 신호(training data) dk와 출력의 차이를 오차 ek = dk - yk로 정의할 때, 식 (5)를 미분한 기울기로 다음과 같은 MEE 알고리듬을 얻을 수 있다[2],[4].
| (6) |
여기서 μ는 수렴 속도와 안정도를 관장하는 스텝 사이즈이다. MEE의 성능 기준(5)와 학습 알고리듬(6) 모두 이중 합산과정이 필요하여 과도한 계산량 또는 시스템 복잡도를 지닌다. 한편, 식 (5)의 이중 샘플 평균 대신 두 순시값 Gσ(ek - ek-1)과 만을 정보 포텐셜로 사용하는 간소화된 정보 포텐셜 를 논문[12]에서 제안하였다.
| (7) |
이 경우, 최소오차 엔트로피는 가 된다.
이렇게 단순화된 식 (7)의 SMEE (simplified MEE) 성능 기준을 사용하여 TDL의 가중치를 갱신하면 다음과 같은 SMEE 알고리듬을 얻게 된다[12].
| (8) |
더 이상 합산과정이 필요 없는 단순해진 SMEE 알고리듬(8)이 기존 MEE 알고리듬인 식 (6)과 비교할 때 크게 감소한 계산량을 가지고 있음을 알 수 있다.
그러나 상숫값의 커널 폭 σ는 특정 상황에 맞는 값으로 선택되어야 하므로 변화하는 통계적 환경에 대처할 수 없다. 또한 식 (6)과 식 (8)의 분모에 공통으로 σ2이 있어서 큰 σ값에서는 가중치 갱신이 무효화되고 작은 값일 때에는 쉽게 불안정해짐을 알 수 있다. 성능에 민감하게 영향을 미치는 이 커널 폭은 적절한 적응추정이 필요한 실정이다.
Ⅲ. 적응적 커널 추정법이 적용된 SMEE 알고리듬
오차 전력의 평균변화율을 활용하여 커널 폭을 갱신하는 적응 커널 알고리듬을 정리하면 다음과 같다. 미소 커널 폭 변동 Δ에 오차 전력이 어떻게 변동하는가를 나타내는 오차 전력 평균변화율을 도출하기 위해, 현재 커널 폭 σo와 미소 증분을 가진 커널 폭 σΔ = σo + Δ, 두 변수가 필요하다. 폭 σo를 채용하여 출력 을 내는 주필터, 폭 σΔ를 채용하여 출력 을 내는 부필터, 이렇게 두 가지 필터를 병용한다. 오차 또한 eo,k = dk - yo,k와 eΔ,k = dk - yΔ,k로 과거 N개 샘플들이 평균된 주필터 오차 전력 ε(eo,k)와 부필터 오차 전력 ε(eΔ,k)를 다음과 같이 얻을 수 있다.
| (9) |
| (10) |
오차 전력 차이 (error power difference, EPD)를 EPD = ε(eΔ,k) - ε(eo,k) 라고 정의하면 미소 커널 폭 변동 Δ에 오차 전력이 어떻게 변동하는가를 나타내는 오차 전력 평균변화율은 다음과 같이 구할 수 있게 된다.
| (11) |
식 (11)을 기울기로 활용하고 커널 폭 갱신을 위한 스텝 사이즈 μσ를 steepest descent 방법에 적용하면 다음과 같은 적응 커널 폭 갱신 알고리듬을 얻을 수 있다[14].
| (12) |
| (13) |
식 (12)와 식 (13)의 적응 커널 폭 추정방식을 채용한 SMEE 알고리듬 (이 논문에서 SMEE with kernel width adaptation, SMEE-KWA라 하겠다)을 식 (14)-(18)과 같이 제안한다.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
여기서, 이 적응적 커널 폭 조절 방법이 적용된 SMEE 알고리듬이 제대로 작동하는지와 어떤 특성들이 나타나는지를 충격성 잡음과 다중경로 채널 환경에서 채널등화 성능실험을 통해 알아본다. 비교 대상으로 기존 MEE 알고리듬에 식 (12)와 식 (13)의 적응 커널 폭을 채용한 MEE-KWA (MEE with kernel width adaptation)는 다음과 같다[14].
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
한편, SMEE-KWA와 MEE-KWA의 커널 조절에 필요한 계산량은 EDP 계산과정이 같으므로 가중치 갱신 과정에서 달라진다. 즉, 식 (14)를 1 operation, O(1)이라 하면 식 (19)는 O(N2)의 계산량이 필요함을 알 수 있다. 따라서 커널 폭 추정과정에서도 SMEE-KWA가 가지는 계산량 감소 효과는 상당하다 할 수 있다.
Ⅳ. 실험 및 결과
간소화된 SMEE에 적응 커널 폭이 적용된 SMEE-KWA 알고리듬과 기존의 MEE에 커널 폭 적응 조절이 가능한 MEE-KWA를 충격성 잡음 있는 다중경로 무선통신 채널의 equalization 성능으로 비교 분석하고자 한다.
그림 1의 기저대역 통신시스템에서 심볼집합 {±1,±3}의 한 심볼이 무작위로 선택된 dk가 채널 H(z)을 통해 전송된다. 스펙트럼 널(spectral null)을 가지는 채널 모델 CH1을 사용했으며 전송함수 (transfer function)은 다음과 같다[17].
| (24) |
채널을 통과한 신호에 분산 0.001의 백색 가우시안 잡음과 세 가지 발생률(α = 0.02, 0.04, 0.06), 분산 50의 랜덤 충격파 (impulses)로 이루어진 충격성 잡음 nk가 더해져 등화기(equalizer)에 입력된다[14],[18].
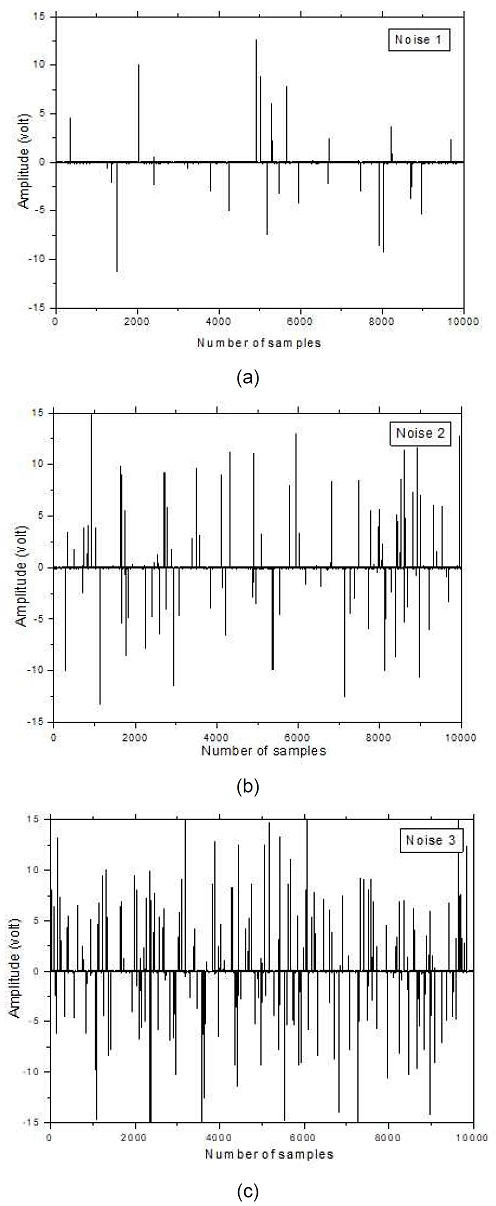
충격 잡음(impulses)의 발생률에 따라 커널 폭 적응 조절이 어떤 영향을 받는지 살펴보기 위해 사용될 다음 세 가지 잡음 샘플, Noise1, Noise2, 그리고 Noise3을 그림 2에 나타냈다.
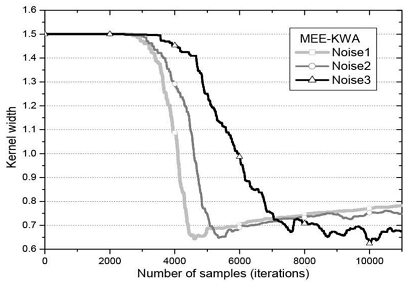
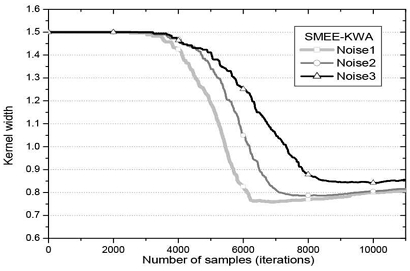
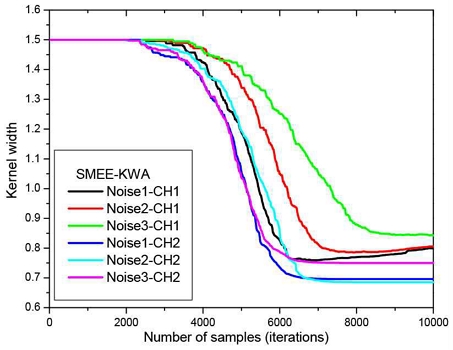
학습 알고리듬에 사용된 파라미터들은 μ = 0.01 (MEE-KWA는 μ/2N2), 초기 커널 폭 σo,0 = 1.5, Δ = 0.01, μσ = 0.002, N = 20로 하였다. 각 잡음 조건에 따른 MEE-KWA의 커널 폭의 수렴 곡선을 그림 3에, SMEE-KWA의 수렴 곡선을 그림 4에 나타냈다.
우선, 그림 4로부터 이 연구에서 제안한 SMEE-KWA는 충분한 커널 폭 적응추정 능력을 지니고 있음을 알 수 있다. 두 번째 관찰된 특징으로, 잡음 Noise1의 경우, 그림 3의 MEE-KWA가 4500 샘플에서 수렴하였다고 보면, 그림 4의 SMEE-KWA는 6000 샘플 정도에서 수렴하여 논문 [12]의 결과와 같이 수렴 속도에서 뒤지는 차이가 존재한다. 그러나 잡음 Noise3의 경우, 두 알고리듬 모두 8000 샘플 정도에서 수렴하여 잡음의 충격성 정도가 심해진 환경에서는 수렴 속도의 차이를 보이지 않음을 알 수 있다. 그러나 느려진 수렴 속도를 보완하기 위해 식 (12)의 μσ를 적절히 튜닝할 수 있는 연구가 뒤따라야 할 것이다.
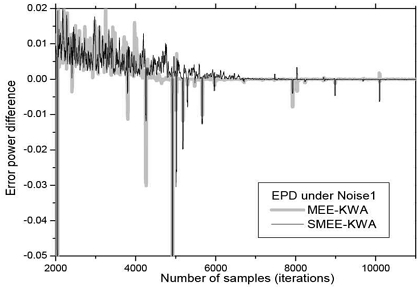
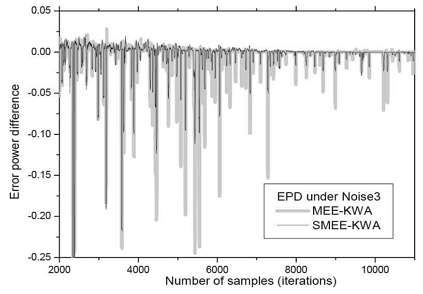
셋째, 두 알고리듬 모두 잡음환경에 따라 커널 폭이 서로 다른 값으로 수렴한다는 점이다. 이 특징은 커널 폭이 변화하는 잡음환경의 경우 통계적 특성에 맞는 커널 폭이 되기 위해서는 기존 방식인 상숫값으로 설정되는 것이 바람직하지 않음을 알려준다. 넷째, 잡음환경이 열악해질수록 MEE-KWA는 커널 폭이 작아지는 경향이, SMEE-KWA는 커지는 쪽으로 수렴한다는 점이다. 열악한 잡음환경일수록 큰 커널 폭으로 지향하는 점은 SMEE-KWA의 수렴이 더 안정적임을 말해준다. 다섯째, 잡음환경이 열악해질수록, MEE-KWA의 커널 폭 수렴 곡선은 수렴 후에 변동(fluctuation)을 보이는 반면, SMEE-KWA의 수렴 곡선은 불안정한 변동 없이 안정된 곡선을 보인다는 점이 특징이다. 이 점 또한 열악한 잡음환경일수록 SMEE-KWA의 수렴이 더 안정적임을 보여준다. 이 특징을 확인하기 위해 두 오차 전력 ε(eo,k)와 ε(eΔ,k)의 차이를 관찰할 필요가 있다. 이에, 미세 커널 폭 차이 Δ에 대해 두 오차 전력 차이인 EPD = ε(eΔ,k) - ε(eo,k)를 Noise1 환경에 대해 그림 5에, Noise3 환경에 대해 그림 6에 나타냈다. 여기서 Noise2 환경은 Noise1 또는 Noise3 환경과 차이를 그래프로 구분하기 어렵다고 판단되어, 잡음 정도에 따른 극명한 차이를 보여주기 위해 Noise1과 Noise3에 대한 미세 오차 전력을 두 그림 5와 6에 나타냈다.
그림 5와 6을 비교하면 열악한 잡음환경일수록 두 알고리듬의 EPD는 큰 차이를 보이는 것을 알 수 있다. 수렴이 시작되며 벌어진 두 알고리듬의 EPD 차이는 수렴 후에도 나타나며 MEE-KWA가 더 큰 값을 가진다. 즉, 커널 폭의 미소 증분 Δ에 대해 오차 전력 차 EPD = ε(eΔ,k) - ε(eo,k)가 수렴 후에도 크다는 것은 충격성 잡음의 영향에 MEE-KWA가 더 민감하며 이 때문에 커널 폭 조절을 위한 기울기 식 (11)이 불안정해지고 식 (12)의 커널 폭은 그림 3과 같이 수렴 후에도 변동(fluctuation)을 나타내는 것으로 판단된다.
한편, 커널 폭 수렴과정이 잡음의 성질에만 의존하는 것이 아니라 채널의 특성에 따라 달라질 수 있는지 살펴볼 필요가 있다. 이에 식 (25)의 다른 채널 모델 CH2에 대한 커널 폭 수렴 곡선을 그림 7에 나타냈다.
| (25) |
CH2에 대한 커널 폭 수렴 곡선은 채널 특성이 열악한 CH1의 경우보다 더 빠르고 부드러운 수렴을 보인다. 또한 수렴된 최적 커널 폭은 CH1의 경우보다 더 작은 값을 가짐을 알 수 있다. 따라서 잡음 상태와 채널 상태 등 통신 환경이 열악할수록 최적 커널 폭은 약간 큰 값이 됨을 알 수 있다. 따라서 잡음 및 채널 특성이 달라지는 상황의 경우 적응적 커널 폭 추정이 필요함을 알 수 있다.
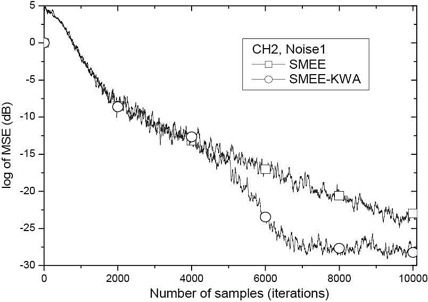
한편, KWA를 적용한 SMEE-KWA 알고리듬이 기존 SMEE 알고리듬보다 어느 정도 더 좋은 MSE 수렴 성능을 도출할 수 있는지를 다음 그림 8에 나타냈다. 비교 환경으로 Noise1이 가해진 채널 CH2에 대해 대표적으로 비교하였다.
그림 8에서 고정 커널 폭을 가진 기존 SMEE 알고리듬이 샘플 시간 10000에서도 수렴하지 못하지만, 적응 커널 폭을 가진 SMEE-KWA 알고리듬은 6000 샘플 근방에서 수렴을 이루고 있음을 알 수 있다. 이에 그림 7에서 보여준 커널 폭의 적응 조절 능력이 MSE 수렴 성능에서 탁월한 성능을 도출함을 알 수 있다.
Ⅴ. 결 론
MEE 기반의 적응 알고리듬이 충격성 잡음과 같은 비가우시안 환경에서 효능을 발휘하며 활발하게 연구되고 있으나 이중 합산의 과중한 계산량 문제와 성능에 민감하게 작용하는 커널 폭 설정 문제를 해결할 필요가 있다. 잡음환경에 따라 커널 폭이 다른 값으로 수렴하는 실험 결과로부터, 변화하는 잡음 및 채널의 특성에 맞는 커널 폭이 되기 위해서는 적응적 커널 폭 추정이 필요함이 입증되었다. MEE 기반 가중치 갱신 알고리듬의 분모에 존재하는 σ2으로 커널 폭 적응추정이 쉽지 않으므로 오차 전력 평균변화율 접근법은 커널 폭 적응추정의 좋은 대안이 될 수 있다. 오차 전력 평균변화율 기반의 커널 폭 적응추정법을 적용한 SMEE-KWA는 MEE-KWA에 비해 수렴 속도에서 미소한 단점을 보이나 계산량의 획기적 감소와 커널 폭의 안정적 적응추정이라는 큰 장점이 있다. 이에 제안한 SMEE-KWA를 신호처리, 기계학습, 상태추정 및 제어, 무선통신 채널 등화가 등에 적용할 때 더욱 높은 구현의 효율성과 성능 신뢰성이 기대된다. 뒤따라야 할 연구로 채널 환경에 따라 느려진 수렴 속도를 보완할 수 있는 연구가 필요하다.
Acknowledgments
본 과제(결과물)는 2022년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다(2022RIS-005).
References
- J. Principe, D. Xu, and J. Fisher, Information theoretic learning, in Unsupervised adaptive filtering, Vol. 1, New York: Wiley, pp. 265-319, 2000.
-
D. Erdogmus and J. C. Principe, “An error-entropy minimization algorithm for supervised training of nonlinear systems,” IEEE Transactions on Signal Processing, Vol. 50, No. 7, pp. 1780-1786, July 2002.
[https://doi.org/10.1109/TSP.2002.1011217]

- N. Kim, “Performance analysis of entropy-based decision feedback algorithms in wireless shallow-water communications,” in Proceedings of KSII Summer Conference, pp. 185-186, June 2012.
-
N. Kim and K. Kwon, “Normalized Minimum Error Entropy Algorithm with Recursive Power Estimation,” Entropy, Vol. 18, No. 7, 239, June 2016.
[https://doi.org/10.3390/e18070239]

-
U. K. Singh, R. Mitra, V. Bhatia, and A. K. Mishra, “Kernel Minimum Error Entropy Based Estimator for MIMO Radar in Non-Gaussian Clutter,” IEEE Access, Vol. 9, pp. 125320-125330, September 2021.
[https://doi.org/10.1109/ACCESS.2021.3111103]

-
L. Dang, B. Chen, S. Wang, W. Ma, and P. Ren, “Robust Power System State Estimation With Minimum Error Entropy Unscented Kalman Filter,” IEEE Transactions on Instrumentation and Measurement, Vol. 69, No. 11, pp. 8797-8808, June 2020.
[https://doi.org/10.1109/TIM.2020.2999757]

-
B. Yang, H. Huang, and L. Cao, “Centered Error Entropy-Based Sigma-Point Kalman Filter for Spacecraft State Estimation with Non-Gaussian Noise,” Space: Science & Technology, Vol. 2022, Article ID: 9854601, July 2022.
[https://doi.org/10.34133/2022/9854601]

- X. Guo, T. Hu, and Q. Wu, “Distributed minimum error entropy algorithms,” Journal of Machine Learning Research, Vol. 21, No. 1, pp. 4968-4998, January 2020.
-
Y. Li, B. Chen, N. Yoshimura, and Y. Koike, “Restricted Minimum Error Entropy Criterion for Robust Classification,” IEEE Transactions on Neural Networks and Learning Systems, Vol. 33, No. 11, pp. 6599-6612, June 2021.
[https://doi.org/10.1109/TNNLS.2021.3082571]

-
S. Huang, Y. Feng, and Q. Wu, “Learning theory of minimum error entropy under weak moment conditions,” Analysis and Applications, Vol. 20, No. 01, pp. 121-139, 2022.
[https://doi.org/10.1142/S0219530521500044]

-
B. Chen, L. Xing, Z. Nanning, and J. C. Principe, “Quantized Minimum Error Entropy Criterion,” IEEE Transactions on Neural Networks and Learning Systems, Vol. 30, No. 5, pp. 1370-1380, September 2018.
[https://doi.org/10.1109/TNNLS.2018.2868812]

- N. Kim and K. Kwon, “A Simplified Minimum Error Entropy Criterion and Related Adaptive Equalizer Algorithms,” JKICS, Vol. 48, No. 3, pp. 312-318, 2023.
-
A. Singh and J. C. Principe, “Kernel width adaptation in information theoretic learning cost functions,” in Proceedings of ICASSP 2010, pp. 2062-2065, March 2010.
[https://doi.org/10.1109/ICASSP.2010.5495035]

-
N. Kim, “A New Kernel-Width Adaptation Method for Minimum Error Entropy,” JKICS, Vol. 46, No. 7, pp. 1131-1137, July 2021.
[https://doi.org/10.7840/kics.2021.46.7.1131]

-
E. Parzen, “On Estimation of a Probability Density Function and Mode,” The Annals of Mathematical Statistics, Vol. 33, No. 3, pp. 1065-1076, September 1962.
[https://doi.org/10.1214/aoms/1177704472]

-
B. Silverman, Density Estimation for Statistics and Data Analysis, New York: Routledge, October 2017.
[https://doi.org/10.1201/9781315140919]

- J. Proakis, Digital Communications, New York, NY: McGraw-Hill, 1989.
-
I. Santamaria, P. Pokharel, and J. Principe, “Generalized correlation function: definition, properties, and application to blind equalization,” IEEE Transactions on Signal Processing, Vol. 54, No. 6, pp. 2187-2197, June 2006.
[https://doi.org/10.1109/TSP.2006.872524]

저자소개

1986년 : 연세대학교 전자공학과(학사)
1988년 : 연세대학교 대학원 전자공학과 (석사)
1991년 : 연세대학교 대학원 전자공학과 (박사)
1998년 ~ 현 재: 강원대학교 교수
※관심분야:통신 신호처리, 정보이론적 학습

1993년 : 강원대학교 컴퓨터과학과(학사)
1995년 : 강원대학교 대학원 컴퓨터과학과(석사)
2000년 : 강원대학교 대학원 컴퓨터과학과(박사)
1998년 ~ 2002년: 동원대학 인터넷정보과 교수
2002년 ~ 현 재: 강원대학교 정보통신공학과 교수
※관심분야:패턴 인식 (Pattern Recognition), 사물 인터넷 (IoT), 기계학습