ElasticNet(LASSO)+RF+HMM을 활용한 지식 그래프의 선후관계 분석 : K-12 수학 문항평가 데이터를 중심으로
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
본 연구는 지식 개념의 선후관계를 밝히기 위해 연속적인 순서의 관측치로부터 은닉된 학습 상태를 추정할 수 있는 HMM을 활용한 분석모델을 설계하였다. 또한, 회귀계수 축소법인 LASSO 파라미터를 이용한 Elastic Net과 Random Forest를 적용하여 유의미한 관계를 도출함으로써 문제 영역을 축소하였다.ElasticNet(LASSO)+RF+HMM 모델에 초등 수학 문항평가 데이터를 적용하여 실험한 결과 이전 연구인 MSMM 기법을 적용했을 때보다 정확도 기준 평균 7% 향상되었다. 본 연구는 학생들의 추측이나 실수를 확률적으로 교정할 수 있는 KC 선후관계의 모델적 틀을 제시했다는 점에서 의의가 있다. 또한, 학습 데이터에서 전문가가 예측하지 못한 지식 관계를 업데이트하여 학습자의 지식 습득 상태에 따라 적절한 학습 경로를 안내하는 맞춤형 교육에도 기여할 것으로 기대된다.
Abstract
This study proposes the analysis model using HMM that can estimate the learning state hidden from observations in a continuous sequence in order to reveal the prerequisite relations among the knowledge concepts(KC). Also, the problem domain was compressed with meaningful KC relations by applying Elastic Net with LASSO parameters and Random Forest, which are regression coefficient reduction methods. As a result of applying elementary mathematics evaluation data to the ElasticNet(LASSO)+RF+HMM model, the average accuracy is improved by 7% compared to the previous study applying MSMM method. This study presents a model framework of the KC prerequisite relations that can make probabilistic correction for students' guesses or mistakes and contributes in that personalized education guides the appropriate learning path according to the learner's knowledge status by improving the knowledge concept relations.
Keywords:
Prerequisite Relation, Knowledge Graph, ElasticNet(LASSO), Random Forest, Hidden Markov Model키워드:
선후관계, 지식그래프Ⅰ. 서 론
갑자기 들이닥친 팬데믹의 전 세계적인 유행으로 공간 이동이 제한되면서 사람들의 일상적인 활동뿐만 아니라 사회 전반의 업무와 소통 방식도 비대면 유형으로 급격하게 변화하고 있다[1]. 교육 현장 역시 불가피하게 학생들의 학습을 온라인으로 지도하고 평가할 수 있는 인터넷 기반의 학습 관리 시스템(LMS, learning management system)이 빠르게 자리 잡는 추세이다. 김상미[2]에 의하면 코로나 19 이후 온라인 교육에 관한 국내 언론 보도기사를 분석한 결과 온라인, 디지털, 원격 수업 등에 관한 기사가 매우 높은 비중을 차지하고 있으며 이는 교육 내부의 관점에서 논의되던 온라인 교육이 사회가 주목하는 주제가 되었음을 의미한다. 외부 환경 요인에 의해 가속화되긴 했으나 기존의 교육환경 속에서 효율적으로 학습 콘텐츠를 제공하고 학습 진도를 관리하는 LMS뿐만 아니라 온라인 MOOC((massive open online course)와 같은 개방형 온라인 교육 플랫폼은 시공간에 상관없이 원하는 강의를 수강할 수 있도록 서비스를 제공하는 등 온라인 교육 시스템을 활용한 교육의 디지털 전환(digital transformation)은 이미 진행되어 왔다[3]. 교육환경을 온라인 시스템으로 구축하게 되면 학습 자료, 학습 태도, 평가 결과 등 교육 데이터를 디지털 데이터 형태로 수집할 수 있게 된다. 이로부터 빅데이터 혹은 인공지능 기술을 활용하여 개인별 학습 상태를 분석하거나 맞춤형 지도를 하는 개인 맞춤형 교육(personal adaptive learning)을 할 수 있는 토대를 마련할 수 있다. 이를 포함하여 학습자에게 개인별로 적합한 교육을 적절한 시기에 제공할 수 있도록 지원하는 기술 관련 분야가 에듀테크(edutech) 혹은 AI 튜터링 분야이다[4].
교육의 디지털 전환의 핵심이라 할 수 있는 에듀테크에서 가장 주목받는 것이 인공지능을 활용하여 개인 맞춤형 학습 지원 기능이다[5, 6]. 개인의 학습 패턴과 결과를 바탕으로 현재의 학습 상태를 파악해 주고 적절한 학습 경로를 추천하기도 한다. 이처럼 학습자의 학습 상태를 판단하거나 이에 따라 학습 경로를 추천하기 위해서는 학습할 지식 개념(KC, knowledge concept)의 구조, 즉 KC 간 유사도 혹은 선후관계를 나타내는 KC맵((knowledge concept map)을 적절하게 구성해야 한다. 어떤 과목의 지식 개념의 구조와 학습 경로는 통상적으로 교수자에 의해 커리큘럼으로 정의된다. 그런데 실제 학습자에게 어떤 지식 개념을 이해하기 위해 다른 지식 개념의 습득 여부가 끼치는 영향은 교수자가 의도한 커리큘럼의 위계와는 다르거나 숨겨진 양상을 보일 수 있다. 따라서 해당 과정에서 학습자의 지식 개념(KC)의 습득 여부 정보로부터 KC 간 관계를 파악하여 기본 커리큘럼을 보완함으로써 실질적인 KC맵을 도출한다면 이후 학습자에게 정밀하고 효과적인 학습 코칭을 할 수 있다. 최현희 등[7]은 KC 간의 선후관계를 규명하기 위하여 KC 관계분석 모델에 Markov 모형인 MSMM(multi-state markov model)을 추가하였고, ARM(association rule mining)만으로 KC 선후관계를 발견한 경우보다 2배 이상의 정확도가 향상하였음을 보였다. 그러나 MSMM은 답안의 확률적 성격을 고려하지 않는다. 가령 병원 감염 여부에 따른 질병-사망 모델을 분석하기 위해 환자의 발병 여부, 입원 여부를 분석 데이터로 사용하는 경우, 무시할 수 없을 만한 오차가 발생하지 않으므로 관찰된 데이터를 직접 사용하여 MSMM을 이용한 모형화가 가능하다. 반면 학습자의 답안으로부터 ‘모름’, ‘습득’과 같은 지식 개념의 습득 여부를 측정할 경우 해당 답안에는 추측 또는 실수와 같은 확률적 변인이 내재해있다. 따라서 관측치뿐만 아니라 이로부터 은닉된 학습 상태에 대한 추정이 필요한데 MSMM을 활용하는 것에는 한계가 있다. 이를 극복하기 위해 본 연구에서는 회귀계수 축소법 중 LASSO 파라미터를 이용한 Elastic Net(ElasticNet(LASSO))과 Random Forest(RF)를 적용한 후 HMM(hidden markov model)을 활용한 KC 선후관계 분석 모델을 설계하였다. HMM은 시간 또는 연속적인 순서를 따르는 관측치로부터 은닉된 상태 값을 추정할 때 유용하다[8]. 본 연구에서 설계한 ElasticNet(LASSO)+RF+HMM 모델에 초등 수학 학습 서비스에서 수집된 문항평가 데이터를 적용하여 실험하였는데 III 장에서 본 연구의 실험에 적용한 데이터의 구성과 특징을 상세히 설명하였다. 이어서 본 연구에서 제안한 분석 모델의 구조와 KC 관계를 분석하는 과정을 단계별로 구체적으로 설명하였다. IV 장에서는 ElasticNet(LASSO)+RF+HMM 모델에 데이터를 적용한 결과를 분석하였다. 이를 통해 학습 데이터를 사용한 KC 모형화가 필요한 경우 HMM 기법을 활용하여 관측치로부터 숨겨진 성질을 고려함으로써 좀 더 정확한 KC 간 선후관계를 도출할 수 있음을 확인하였다.
본 연구에서 제안한 ElasticNet(LASSO)+RF+ HMM을 활용한 KC 선후관계 분석 모델은 답안 응답에 영향을 주는 학습자의 확률적 선택을 고려하는 선후관계분석 연구에 기여할 것으로 기대된다.
Ⅱ. 이론적 배경
서로 다른 KC 간의 관계를 설명할 때 두 KC 사이의 상관분석을 통하여 상관계수의 고저를 판단하거나 단순 회귀분석을 수행하여 회귀계수의 유의성을 확인할 수 있다. 그러나, 개별 KC를 좀 더 정확히 설명하기 위하여 여러 다른 KC들의 혼합을 설명변수로 고려해야 한다면 이 KC들을 하나의 모형에서 동시에 고려한 회귀분석이 필요하다. 이때에는 다중선형 회귀 모델을 적용하게 된다.
2-1 정규화(Regularization)
독립변수가 여러 개가 적용되는 다중 선형 회귀 모델은 과대적합(overfitting)될 때가 종종 있다. 이를 차원의 저주(curse of dimensionality)[9]라고 부른다. 과대적합이 발생하면 훈련 데이터에만 잘 맞도록 학습되므로 훈련 데이터가 조금만 바뀌더라도 학습 결과가 크게 바뀔 수 있으며 개발된 모형은 과대 차원으로 일반화 능력이 떨어지게 된다. 이것을 해결하기 위해 선형 모형에서는 정규화 방법으로 LASSO 회귀, Ridge 회귀, Elastic Net을 제안한다. 이들 방법은 파라미터의 값에 제약을 가함으로써 모델을 정돈해서 과대적합을 피할 수 있게 한다.
LASSO(least absolute shrinkage and selection operator) 회귀(이하 LASSO)는 예측의 정확도와 이해 가능성을 높이려는 목적으로 변수 선택과 정규화를 수행하는 회귀분석 방법으로 Robert Tibshirani에 의해 정의되었으며 지구 물리학에서 최초로 소개되었다[10].
를 i 번째 특성 벡터(feature vector)라고 하고, N개의 관측치에 대해서 p개의 변수가 존재한다고 하자. yi를 결괏값이라 하면 LASSO의 목적함수는 식 (1)과 같다.
| (1) |
식 (1)에서 β0는 상수항, β는 회귀계수, t는 정규화의 강도를 결정하는 자유 파라미터이다. LASSO는 최적화를 수행하면서 덜 중요한 변수들의 회귀계수 βj를 0으로 만들기 때문에 변수를 선택하는 효과가 있다. 예를 들어 교육 데이터로 지식 개념(KC) 관련 데이터를 고려한다면 학습자의 시험 점수로 수량화한 KC1, KC2, ..., KCn이 설명변수 혹은 목적변수가 된다. 만일 KC1이 목적변수이고 나머지 KC2 ~ KCn이 특성변수들이라면 LASSO 모형을 사용할 경우 KC1과 연관성이 높으면서 다른 KC들과는 상관이 약한 KC를 골라 유의미한 관계가 있는 KC의 쌍을 고를 수 있다.
Ridge 회귀(이하 Ridge)는 LASSO와 유사한 목적으로 만들어졌으며, LASSO의 목적함수인 식 (1)의 조건항에서 회귀계수 βj에 대한 절댓값항을 제곱항으로 변형한 것이다[11]. 이처럼 절댓값이 아닌 제곱을 취함으로써 관련이 없는 항의 회귀계수들을 0이 아니라 0에 가까운 값으로 만들 수 있으므로 변수 선택의 효과는 크지 않을 수 있다. 그러나 제곱항을 사용함으로써 미분이 가능하게 되어 경사 하강법(gradient descent) 최적화를 할 수 있다는 장점이 있다.
Elastic Net은 회귀 모형의 회귀계수 축소 방법인 LASSO와 Ridge를 동시에 고려한 모형으로 회귀계수가 특성변수 간의 상관에 의하여 무한정 커지는 것을 막는 역할을 한다[12]. 교차검증 과정을 통하여 선형 회귀의 제약조건으로 추가한 항에 대한 계수의 최적값을 고를 수 있다는 장점이 있다. 행렬 표현식을 빌려 제약 조건을 고려한 평균제곱오차(MSE, mean square error)를 최소화하여 얻는 β의 추정치는 식 (2)로 나타낼 수 있다.
| (2) |
Elastic Net 모형에서 고려하는 y, β, t의 의미는 LASSO와 동일하며 X는 입력 벡터를 나타낸다. 식 (2)의 조건식에서 |β|는 LASSO, |β|2은 Ridge 제약조건에 해당하며, Elastic Net 함수의 교차검증(cross validation)을 사용함으로써 매우 적절한 α값을 찾을 수 있다는 강점이 있다.
2-2 Random Forest
Random Forest 알고리즘은 부트스트랩 샘플링 기법을 이용하여 다수의 데이터셋을 생성한 후 각각의 데이터셋에 대하여 의사결정트리 알고리즘을 적용하여 데이터셋과 동일한 크기의 트리 모형을 생성하도록 한다[13]. 알고리즘의 최종 예측값은 각각의 트리에서 예측된 값을 평균하거나 투표한 값이다.
최현희 등[7]은 KC 간의 관계를 찾기 위하여 신뢰도 및 지지도에 기반하여 규칙을 정리하는 ARM(association rule mining)을 활용하였다. ARM은 데이터의 특성을 추출한다는 면에서는 유의미하나, 데이터에서 발견되는 작은 변화로 인하여 발견하는 값들이 크게 달라지기 때문에 신뢰할 수 있는 결과를 얻기 어렵다. 다만 ARM의 앙상블 버전을 Random Forest 알고리즘으로 간주할 수 있다[14].
Random Forest 알고리즘의 강점은 목적변수에 대한 특성변수들의 중요도를 계산해 준다는 것이다. 중요도를 계산하는 알고리즘은 대표적으로 지니 중요도(gini importance)와 퍼뮤테이션 중요도(permutation importance)로 요약된다[15]. 지니 중요도는 트리 모형에서 각 변수가 분류될 때 불순도의 감소분을 고려하는 알고리즘이며, 퍼뮤테이션 중요도는 OOB(out-of-bag) 샘플에 존재하는 변수들 중 하나를 골라 무작위로 섞은 데이터를 트리에 흘려보냈을 때의 예측값의 차이로부터 계산된다. 본 논문의 실험에서는 특성변수 중요도의 계산에 퍼뮤테이션 중요도를 활용하였다.
2-3 HMM (Hidden Markov Model)
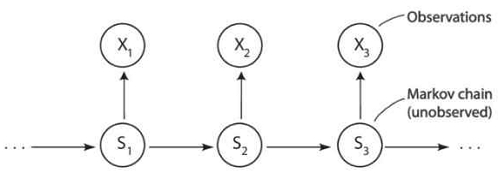
시간 또는 연속적인 순서를 따르는 관측치들이 존재할 때 관측된 값이 직접적으로 확인 불가능한 은닉된 상태에 영향을 받는다는 가정이 있다면 HMM을 활용할 수 있다. 그림 1과 같이 입력 데이터를 x1 x2 x3 x4 ... xt라고 할 때 이러한 xi들이 s1 s2 s3 s4 ... st 의 영향을 받아 일어난다면 HMM을 기반한 모형화를 고려할 수 있다. 가령, 학생이 어떤 개념을 습득했는지 정확히 관측하기는 어려우나 해당 개념에 관한 시험의 문항별 정확도가 습득 여부의 영향을 받아 나타나므로 HMM을 통해 모형화할 수 있다. 학생이 시험에서 t개의 문제를 풀고 얻은 점수를 x1 x2 x3 x4 ... xt로 표현하고 학생이 가진 이해도 자체는 s1 s2 s3 s4 ... st로 구성한다. 이때 응답 점수인 x1 x2 x3 x4 ... xt는 ‘정확’, ‘부정확’과 같은 이산화(discretization)된 값을 가져야 한다.
은닉상태의 수가 m개라면 관측치 x의 확률분포 p(x)는 식(3)과 같이 표현되며 이는 선형혼합모형(linear mixture model)의 형태와 유사하다[8].
| (3) |
HMM을 활용하여 풀 수 있는 문제는 학습 데이터로부터 식 (4)에 나타난 HMM의 파라미터 θ를 계산하는 것 등으로 구성되어 있다.
| (4) |
우리의 관심사인 KC의 순서를 결정하는 문제도 HMM 파라미터 θ를 구하는 과정에서 얻어질 수 있다. 가령, KC에 대한 2개의 은닉상태를 ‘모름(unlearned)’, ‘습득(learned)’으로 나타내면, HMM에 대한 EM(expectation maximization) 알고리즘으로 알려진 Baum–Welch 알고리즘[16]을 수행하여 그 결과인 HMM의 파라미터 θ를 구하는 과정 중에 식 (5)와 같은 A(전이확률) 행렬을 얻을 수 있다.
| (5) |
Ⅲ. 연구 설계
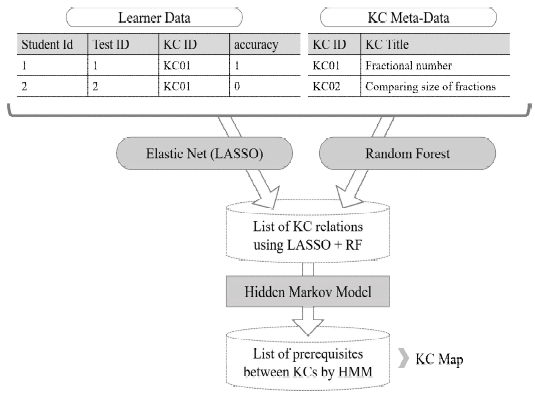
본 연구에서는 KC 간 선후관계를 도출하기 위해, 그림 2와 같이 우선 전체 KC에서 강한 연관성을 보이는 KC의 쌍들을 선택한 후 각 KC 쌍의 선후관계를 결정하는 방법을 사용하는 단계적 방법론을 취하였다. 즉, 첫 번째 단계에서 Elastic Net(LASSO)과 Random Forest 알고리즘을 사용하여 연관성이 높은 KC 쌍을 선택한다. 두 번째 단계에서는 첫 번째 단계에서 추출된 KC 쌍의 선후관계를 결정하기 위해 관측치들의 확률적 오류를 고려하여 HMM을 적용하였다.
3-1 연구 데이터의 구성
KC 간 선후관계 분석을 위하여 D사의 온라인 수학 학습 서비스에서 수집되는 문제풀이 로그 중 레벨 평가 데이터를 활용하였다. 이 중 초·중등 학생을 대상으로 하는 11레벨부터 15레벨까지의 레벨 평가 로그를 연구 데이터로 선정하였다. 학습자는 교수자의 판단에 따라 3회까지 레벨 평가에 재응시할 수 있다. 그러나 3회까지 응시하는 학생의 수가 적으므로 학습자의 수를 고려하여 본 연구에서는 2회까지의 데이터를 활용하였다. 표 1은 본 연구에 활용한 학습 데이터를 구성하는 각 레벨의 평가 로그의 수, 평가를 수행한 학생의 수, 해당 레벨에서 공부해야 하는 KC의 갯수를 나타내고 있다.
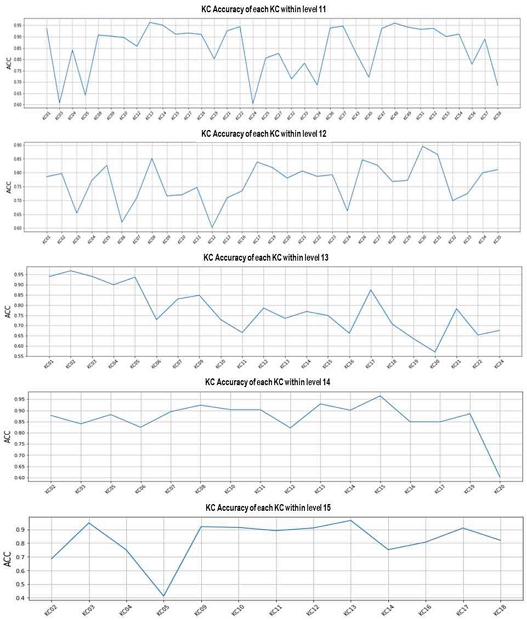
그림 3은 각 레벨의 KC들에 속한 각 문항에 대하여 0(모름)과 1(습득)로 측정된 응답을 KC 별로 평균한 값으로 각 레벨 내 KC 별 학습의 정확도를 표현한 것이다.
3-2 연관성이 있는 KC쌍의 추출
본 연구에서는 KC 간의 연관성을 찾아내는 작업을 상관계수와 회귀계수의 수학적 연관성에 근거하여 상관분석에서 회귀분석의 문제로 확장하고자 한다[17]. 어떤 KC에 대해 연관성이 있는 다른 KC가 존재한다고 가정하고 KC의 이름을 변수라 하면, 관련 KC들의 관측치로부터 유의미한 관계의 목적변수와 특성변수의 쌍을 관찰할 수 있다.
한 KC에 여러 개의 평가 문제가 포함되어 있다면 해당 문제들의 테스트 결과로부터 해당 개념의 습득 여부를 판단할 수 있다[18]. 즉, 특정 KC에 관련된 문제들의 정확도의 평균값을 해당 KC의 습득 여부를 확인하기 위한 대푯값으로 활용할 수 있다. 회귀분석의 문제로 다시 돌아가서 보면 이 평균값들의 관련성은 KC 간, 즉 목적변수로 쓰인 KC와 특성변수 KC 간의 관련성으로 고려할 수 있다. 표 2는 KC 간 관계를 얻어내기 학습자별 문제풀이 학습 로그로부터 KC 별 평균값을 계산하여 생성한 데이터셋을 보여주고 있다.
HMM 모형은 마르코프 성질(markov property)를 가정한다. 그러므로 KC의 문제풀이 결과의 평균값들이 순차적으로 입력되었다고 하면 특정 KC가 목적 KC에 영향을 주는 KC로 선택되었다 할 때 마르코프 성질에 의해 그 특정 KC에 영향을 주는 다른 KC들은 설명변수 리스트에서 배제되어야 한다. 예를 들어, y가 KCi이고 X는 KCi를 제외한 KCj(i ≠ j)인 회귀 모형이 있다고 하자. HMM 모형을 고려한다면 입력으로 사용되는 X 간의 영향 관계 또는 연관성이 배제되어야 하므로 설명변수 간의 독립성을 보장하는 LASSO 회귀 모형을 활용할 수 있다. 그런데 단순 LASSO는 교차검증 과정을 고려하지 않으므로 본 연구에서는 LASSO 모형과 교차검증을 모두 달성할 수 있는 Elastic Net 모형을 활용한다.
회귀분석에서 유의수준 값을 5%라 하면 설명변수들의 p-value가 0.05보다 작게 나오는 경우 모두 통계적으로 유의한 변수로 받아들인다. 이때 유의한 변수를 복수 개 얻게 된다면 복수 개의 연관관계를 얻게 되고 복수 쌍들 간의 의미 있는 서열화가 문제가 될 수 있다. 즉, 선형 모형에 근거한 Elastic Net(LASSO) 모형만으로는 유의수준 내에 존재하는 관계들 사이의 중요도에 따른 서열화가 불가능하다. 따라서 선형 모형을 고려한 Elastic Net(LASSO) 모형에서 유의수준을 만족하는 관계 리스트를 얻었다면, 비선형 모형으로 중요도 값을 산출해 주는 Random Forest 알고리즘을 추가하여 발견된 관계들에 대한 신뢰도를 높임과 동시에 유의수준 내 관계들에 대한 서열화를 시도할 수 있다.
본 연구에서 제안하는 유의미한 관계를 갖는 KC 쌍을 도출하기 위해 Elastic Net(LASSO)과 Random Forest를 적용하는 절차를 다음과 같이 요약할 수 있다.
- ① Elatic Net(LASSO)을 이용하여 종속 변인 KCi를 설명하는 KCj를 유의수준 0.05 기준으로 선별한다.
- ② Random Forest 모형을 통하여 KCi에 대한 KCj들의 중요도를 계산한다.
- ③ ②의 Random Forest 모형에서 얻은 관계 쌍들 중 상위 10%에 해당하는 관계들을 추출한다.
- ④ ①과 ③에서 추출된 관계들을 최종 관계 쌍에 가장 중요한 연관관계로 저장하고 분석 방법을 BOTH로 설정한다.
- ⑤ ④에서로 충분한 KC 관계 쌍을 얻지 못할 경우, 최종 관계 쌍과 겹치지 않는 관계 중 Elastic Net(LASSO)에서 얻은 연관 쌍에 ②에서 얻은 중요도 정보를 더해 최종 관계 쌍에 분석 방법을 LASSO라고 설정한다.
- ⑥ ⑤에서로 충분한 KC 관계 쌍을 얻지 못할 경우, 최종 관계 쌍과 겹치지 않는 관계 중 Random Forest 모형에서 상위 10% 이내에 드는 관계들을 최종 관계 쌍에 추가하고 분석 방법을 RF라고 설정한다.
3-3 HMM을 이용한 선후관계의 결정
Elastic Net(LASSO)과 Random Forest를 적용하여 연관관계를 갖는 KC 쌍들을 얻었다면 다음으로 각 KC 쌍의 선후를 결정해야 한다.
대상이 되는 KCi와 KCj가 있고 이들이 가지는 값 KC(i)와 KC(j)가 0(모름) 또는 1(습득)이라면 2회의 문제풀이 결과에 따라 0 → 0, 0 → 1, 1 → 0, 1 → 1의 전이확률을 계산할 수 있다. 그러나, 만일 0 또는 1로 나타나는 KCi의 상태 값이 어떤 은닉상태의 영향을 받아 나타난다면 전이확률은 그 은닉상태의 값을 토대로 계산해야 한다. 또한, 연관관계를 얻기 위하여 사용한 값들은 연속형 값을 가졌기 때문에 HMM을 적용하기 전 이를 이분화된 값으로 치환하는 과정이 필요하다[19].
HMM 알고리즘을 이용하면 서로 의존적인 관계를 맺고 있는 HMM의 파라미터 셋인 θ = {π, A, B}를 얻을 수 있다. 여기서 π는 초기확률, A는 전이확률, B는 방출확률이다. 두 KC가 매우 유사한 개념이고 시차만 다르다면 ‘모름’(0)의 비율이 줄어드는 순서대로 두 KC의 선후 관계를 따져볼 수 있다. 그러나 KC를 가장 작은 단위의 서로 다른 지식 개념이라고 볼 때 두 KC의 선후관계는 Chen[20]이 제시한 바와 같이 식 (6)와 식 (7)에 의해 연관관계 (KC(i), KC(j))의 전이확률이 미리 정한 유의수준인 α를 만족한다면 선후관계 KCi→KCj가 성립한다고 판단한다.
| (6) |
| (7) |
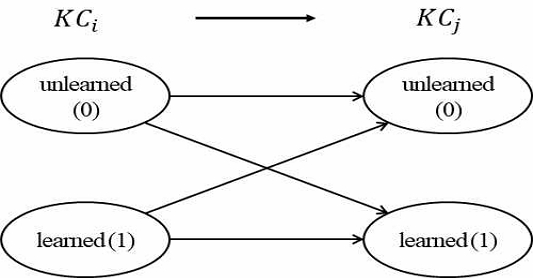
본 연구에서는 HMM의 파라미터를 추정하는 방법인 Baum Welch 알고리즘[6]을 적용하여 그림 4와 같이 모름(KC(i))->모름(KC(j)), 습득(KC(j))->습득(KC(i))의 전이확률을 계산한 후, 이들이 유의수준 α 이상일 때 KCi→KCj의 순서가 있다고 결정한다.
Ⅳ. 결과 및 분석
KC 간 선후관계를 분석하기 위해 일차적으로 연관관계를 추출한 후 이들을 대상으로 각 관계 내 순서를 결정하는 과정을 진행하였다.
4-1 연관관계 도출을 위한 유의수준 결정
각 레벨에서 학습자의 KC별 문제풀이 로그로부터 Elastic Net(LASSO)에서는 0.05의 유의수준을 만족하는 KC 쌍을 고려하였고 Random Forest에서는 특성변수의 중요도가 상위 10% 이상일 경우 연관관계 후보로 추출하였다. 이처럼 유의미한 연관관계를 도출하기 위한 유의수준(0.05, 10%)을 선택하기 위해 Elastic Net(LASSO)에서의 세 가지 유의 확률 조건(0.05, 0.01, 0.001)과 RF의 결과 중 유의미한 상위 중요도를 고르는 세 가지 조건(10%, 20%, EL과 동일한 개수) 과 최종 관계 쌍 리스트에 먼저 적용한 알고리즘에 따른 실험 결과(Elastic Net(LASSO), RF)를 모두 고려한 총 18쌍의 조건에 대하여 성능이 비교적 만족스러웠던 결과를 도출한 조합이다.
표 3에 유의수준 조건에 따른 총 18쌍에 대해 레벨별 정확도를 나타내었다. Method 열은 연관관계 도출 절차를 진행할 때 Elastic Net(LASSO)과 Random Forest(RF) 중 어느 알고리즘을 먼저 사용하는지를 나타낸다. LASSO 열은 연관관계 후보를 도출할 때 Elastic Net(LASSO) 알고리즘에 적용된 유의 수준이다. RF 열은 연관관계 후보를 도출할 때 Random Forest 알고리즘에 적용된 특성변수의 중요도 값이다. 표 3의 4번째와 7번째 행에서 모든 레벨의 중요도가 공통적으로 상위 값을 나타내므로 LASSO의 유의수준 0.05, RF의 특성변수 중요도 10%의 요건으로 정하였다.
표 4는 본 연구에서 적용한 수학 문항평가 데이터 중 15 레벨에서 추출된 연관관계를 나타낸 것이다. 표 4의 before와 after 열은 KC쌍의 선후를 나타낸다. before_title은 해당 연관관계의 선수 KC에 대한 설명이며, after_title은 해당 연관관계의 후수 KC에 대한 설명이다. mapped 열은 본 연구에서 제안한 Elastic Net(LASSO)+RF+HMM 모형을 통해 추출한 연관관계가 타겟 선후관계에 존재할 경우 1로 표기되며, 모형에서 찾아낸 선후관계 목록 중에 mapped가 1인 항목의 비중이 각 레벨의 정확도로 계산된다. 한편, mapped 값이 0인 경우 주어진 타겟 목록에는 없으나 본 연구의 모델이 찾아낸 선후관계로서 학습 데이터로부터 분석되었다는 의미가 있다. 따라서 mapped 값이 0인 선후 관계가 타겟 목록에서 누락되었을 가능성이 있을지 교사에게 검토하도록 제안하고 관련 커리큘럼 혹은 교수법을 보강할 수 있을 것이다. 표 4의 method 열은 각 연관관계를 추출할 때 적용된 알고리즘을 기입한 것으로 BOTH는 Elastic Net(LASSO)과 Random Forest의 순서로 적용되어 검출된 관계, LASSO는 Elastic(LASSO)에서만 추출된 관계, RF는 Random Forest에서만 추출된 관계라는 의미이다.
4-2 KC 선후관계의 분석
앞서 Elastic Net(LASSO)와 RF 기법으로 추출된 KC 연관관계들을 모집단으로 하고 HMM을 적용하여 얻은 전이확률에 기반하여 각 연관관계의 방향을 결정하였다. 앞서 KC의 습득 여부를 문제풀이 점수를 활용하여 측정하는 동안 확률적 요인을 고려하기 위해서 MSMM대신 HMM을 활용해야 함을 언급하였다. 또한, Chen[20]에서 논의된 바와 같이 모름(KC(i)) ->모름(KC(j)), 습득(KC(j))->습득(KC(i))의 전이확률이 α이상일 때 KCi→KCj의 순서가 있다고 보았다.
본 연구에서는 HMM을 이용하여 전이확률을 얻은 후 이 값들이 내포하는 선후 관계를 결정하기 위하여 α를 0.3으로 설정하였는데 이는 D사에서 제공한 전문가가 만든 선후 관계 리스트와 가장 잘 맞는 값이다. 이는 표 4의 direction에서 “forward”로 표시된 것은 확률적으로 before로 나타난 KC가 after로 나타난 KC의 앞에 나와야 함을 의미한다.
4-3 HMM과 MSMM의 적용 결과 비교
ElasticNet(LASSO)+RF+HMM 모형을 이용하여 얻은 선후관계가 있는 KC쌍에 대한 정확도(precision)와 HMM 대신 MSMM을 적용했을 때의 정확도를 비교하였다. 표 5에 나타난 바와 같이 확률적인 면에 대한 고려가 있었을 때 MSMM을 적용했을 때보다 HMM을 적용했을 때 정확도 기준 평균 7% 향상된 것을 확인할 수 있다.
이는 문제풀이 로그와 같은 데이터를 사용하는 KC 모형화가 필요한 경우, 전이확률의 계산에 더하여 보이지 않는 확률적 특성을 추가 고려하는 HMM 알고리즘을 활용함으로써 선후관계 예측에 향상된 정확도를 얻을 수 있다는 것을 보여주고 있다.
Ⅴ. 결론
지식을 습득하기 위해서는 그를 구성하는 세부 개념들을 익히고 연결하는 과정이 필요하다. 어떤 분야의 지식을 구성하는 기본적인 지식 개념(KC)들과 그 습득 순서를 표현한 것이 커리큘럼이다. 커리큘럼을 구성하는 KC들은 대개 순차적으로 표현되나 어떤 특정 개념을 습득하기 위해 반드시 먼저 습득해야 하는 KC 그룹이 존재하기 마련이다. 개인별 맞춤형 학습을 지원하기 위해서는 학습자가 특정 개념을 습득하기 위해 혹은 습득하지 못했을 때 확인해야 하는 선행 KC를 제시할 수 있어야 한다.
본 연구에서는 특정 커리큘럼을 구성한 각 KC 들의 선후관계를 학습자의 실제 학습 데이터로부터 분석하기 위해 Elastic Net(LASSO), RF, HMM 방식을 적용하는 모델을 제안하였다. Elastic Net(LASSO)+RF+HMM을 활용한 KC 선후관계 분석 절차는 다음과 같다. 첫 번째 단계에서 Elastic Net 기반의 LASSO 알고리즘과 RF 분석을 통해 각 KC 별로 상위 10% 이내의 유의미한 상관관계를 갖는 KC 그룹을 도출한다. 두 번째 단계로 각 KC 별로 상관 관계를 보이는 그룹의 KC 요소들에 HMM을 적용하여 선후 관계를 도출한다.
본 연구에서 제안한 Elastic Net(LASSO)+RF+HMM 모델과 최현희 등[7]이 제안한 ARM+MSMM 모델에 각각 초중등 레벨의 수학 평가 데이터를 동일하게 적용한 결과를 비교하였으며, 그 결과 Elastic Net(LASSO)+RF+HMM 모형을 이용하여 얻은 KC 선후관계의 정확도가 평균 7% 향상된 것을 확인할 수 있었다.
본 연구는 ARM + MSMM 모델에서 고려하지 못한 학습 데이터의 작은 변화에 흔들리지 않는 KC 간의 관련성을 찾고 동시에 학생들의 추측 또는 실수에 대한 확률적 보정을 수행할 수 있는 KC 선후관계를 추출할 수 있는 알고리즘을 제시했다는 점에서 그 의의가 있다.
Acknowledgments
본 연구는 2022년도 대교(주) 사의 콘텐츠 개발실의 지원에 의하여 이루어진 연구로서, 관계부처에 감사드립니다.
References
- H. G. Oh, “Analysis of major social changes and information security issues after COVID-19,” Communications of the Korean Institute of Information Scientists and Engineers, Vol. 38, No. 9, pp. 48-56, 2020. https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE09910486
-
S. M. Kim, “Analysis of Press Articles in Korean Media on Online Education related to COVID-19,” Journal of Digital Contents Society, Vol. 21, No. 6, pp. 1091-1100, 2020.
[https://doi.org/10.9728/dcs.2020.21.6.1091]

- K. Lee, S. H. Kwon, C. W. Yang, D. W. Koh, K. B. Kim and M. S. Choi, “Exploring Future School Education Scenarios in the Era of Digital Transformation,” Korean Journal of Teacher Education, Vol. 37, No. 2, pp. 1-25, 2021. http://www.earticle.net/Article.aspx?sn=393898
-
S. Y. Choi, “Artificial Intelligence in Education: A Literature Review on Education Using Artificial Intelligence,” The Journal of Korean Association of Computer Education, Vol. 24, No. 3, pp. 11-21, 2021.
[https://doi.org/10.32431/kace.2021.24.3.002]

-
D. Lee, Y. Huh, C. Lin. and C. M, Reigeluth, “Technology functions for personalized learning in learner-centered schools”, Educational Technology Research and Development, Vol. 66, pp. 1269-1302, 2018.
[https://doi.org/10.1007/s11423-018-9615-9]

- M. Brown, M. McCormack, J. Reeves, D. C Brook, S, Grajek, B. Alexander, M. Bali, S. Bulger, S. Dark, N. Engelbert, K. Gannon, A. Gauthier, D. Gibson, R. Gibson, B. Lundin, G. Veletsianos, and N. Weber, “2020 Educause Horizon Report Teaching and Learning Edition,” EDUCAUSE, pp. 14-16, Louisville, Sep 2022. https://www.learntechlib.org/p/215670/, .
-
H. H. Choi and M. J. Lee. “Analysis of prerequisite relation in knowledge graph using ARM and MSMM: Focusing on problem evaluation data of K-12 math,” Journal of Digital Contents Society, Vol. 23, No. 6, pp. 1131-1140. 2022.
[https://doi.org/10.9728/dcs.2022.23.6.1131]

-
A. Khademi, “Hidden Markov Models for Time Series: An Introduction Using R”, Journal of Statistical Software 80. pp. 1-4, 2017.
[https://doi.org/10.18637/jss.v080.b01]

-
Michel Verleysen and Damien François, “The curse of dimensionality in data mining and time series prediction”, International work-conference on artificial neural networks. Springer, Berlin, Heidelberg, 2005.
[https://doi.org/10.1007/11494669_93]

-
R. Tibshirani, “Regression Shrinkage and Selection via the Lasso,” Journal of the Royal Statistical Society. Series B (Methodological), Vol. 58, No. 1, pp. 267–288, 1996.
[https://doi.org/10.1111/j.2517-6161.1996.tb02080.x]

-
P. J. Brown and J. V. Zidek, “Adaptive Multivariate Ridge Regression,” The Annals of Statistics, Vol. 8, No. 1, pp. 64-74, 1980.
[https://doi.org/10.1214/aos/1176344891]

-
H. Zou and T. Hastie, “Regularization and Variable Selection via the Elastic Net,” Journal of the Royal Statistical Society. Series B (Statistical Methodology), Vol. 67, no. 2, pp. 301–320, March 2005.
[https://doi.org/10.1111/j.1467-9868.2005.00503.x]

-
M. Schonlau and R. Y. Zou, “The random forest algorithm for statistical learning,” The Stata Journal, Vol. 20, No. 1, pp. 3-29, March 2020.
[https://doi.org/10.1177/1536867X20909688]

-
H. Boström, R. B. Gurung, T. Lindgren, and U. Johansson, “Explaining Random Forest Predictions with Association Rules,” Archives of Data Science, Series A (Online First), Vol. 5, No. 1, 2018.
[https://doi.org/10.5445/KSP/1000087327/05]

-
C. Strobl, A. L. Boulesteix, T. Kneib, T. Augustin and A. Zeileis, A. “Conditional variable importance for random forests,” BMC bioinformatics, Vol. 9, No. 1, p. 1-11, 2008.
[https://doi.org/10.1186/1471-2105-9-307]

-
P. M. Baggenstoss, “A modified Baum-Welch algorithm for hidden Markov models with multiple observation spaces,” IEEE Transactions on speech and audio processing, Vol. 9, No. 4, pp. 411-416, May 2001.
[https://doi.org/10.1109/89.917686]

-
J. Schmid Jr, “The relationship between the coefficient of correlation and the angle included between regression lines,” The Journal of Educational Research, Vol. 41, No. 4, pp. 311-313, 1947.
[https://doi.org/10.1080/00220671.1947.10881608]

-
C. Piech, J. Bassen, J. Huang, S. Ganguli, M. Sahami, L. J. Guibas and J. Sohl-Dickstein, “Deep knowledge tracing,” Advances in neural information processing systems, Vol. 28, Jan 2015.
[https://doi.org/10.48550/arXiv.1506.05908]

- C. W. Jung and D. J. Kang, “A Recognition Algorithm of Suspicious Human Behaviors using Hidden Markov Models in an Intelligent Surveillance System,” Journal of Korea Multimedia Society, Vol. 11, No. 11, pp. 1491-1500, 2008. https://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE01605481
-
P. Chen, Y. Lu, V. W. Zheng, X. Chen and B. Yang, “Knowedu: A system to construct knowledge graph for education,” Ieee Access, Vol. 6, pp. 31553-31563, May 2018.
[https://doi.org/10.1109/ACCESS.2018.2839607]

저자소개

1997년 : 고려대학교 대학원 (이학석사)
2019년 : 호서대학교 대학원 (통계학 박사)
1996년~2012년: 한국 IBM 소프트웨어 연구소 부장
2012년~2014년: 환경부 IT 전문위원
2015년~2017년: 데이터 솔루션 수석 컨설턴트
2020년~현 재: 라이브데이터(주) 수석 연구원
※관심분야 : 데이터 분석, 데이터 사이언스, 에듀테크

1994년 : 중앙대학교 컴퓨터공학과 (공학사)
1996년 : KAIST 전산학과 (공학석사)
1996년~2000년: ㈜ LG전자 LG종합기술원 연구원
2000년~2010년: ㈜ 아이에이 수석연구원
2011년~2015년: ㈜ 삼성전자 소프트웨어센터 부장
2016년~현 재: 중앙대학교 다빈치교양대학 조교수
2018년~현 재: 고려대학교 컴퓨터학과 박사과정
2021년~현 재: 라이브데이터(주) 연구소장
※관심분야:SW/AI 교육, AI 리터러시, 기계학습, 에듀테크