벡터자기회귀(VAR)을 이용한 감마선량 이상상황 예측
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
감마선은 인체에 매우 위험하며 천연 또는 인공 물질에 포함되어 있다. 감마선량을 지속적으로 측정하여, 일정 공간 내 방사성 물질 방출의 이상 여부를 확인할 수 있다. 일부 날씨 관련 정보는 공간 내 감마선량과 상호 상관 관계가 있으며, 감마선량 예측에 사용되는 데이터세트는 감마선 측정값과 날씨 데이터의 다변량 데이터 모델을 구성하는 것이 필요하다. VAR(Vector Auto Regression) 모델은 일변량 자기 회귀 모델을 다변량 시계열 데이터로 확장하여, 다변량 시계열의 상호 의존성을 분석하기 위해 가장 널리 사용되는 확률적 프로세스 모델 중 하나이며 시계열의 동작을 설명하고 예측하는 데 유용하다. 본 논문에서는 공공데이터인 감마선량과 날씨 데이터를 활용하고, VAR 다변량 데이터 모델을 통해 기상 변화에 따른 공간 감마선량의 이상 상황 예측이 가능함을 확인하였다.
Abstract
Gamma rays are very dangerous to the human body and are contained in natural or artificial substances. The gamma dose can be continuously measured to determine whether there is an abnormality in the release of radioactive material in a certain space. Some weather-related information is correlated with gamma doses in space, and the dataset used to predict gamma doses requires that a multivariate data model be constructed with gamma ray measurements and multivariate amounts of weather data. The Vector Auto Regression (VAR) model extends the univariate auto regression model to multivariate time series data, making it one of the most widely used probabilistic process models for analyzing the interdependence of multivariate time series, and is useful for explaining and predicting the behavior of time series. In this paper, we use the public data gamma dose and weather data, and confirmed that it is possible to predict anomalies of spatial gamma doses according to weather changes through the VAR multivariate data model.
Keywords:
Gamma rays, Weather Data, Multivariate, ARIMA, Vector Auto Regression키워드:
감마선, 날씨 데이터, 다변량, 자기회귀누적이동평균, 벡터자기회귀Ⅰ. 서 론
감마선은 활성화된 에너지 상태의 원자핵이 더 낮은 상태 또는 지상 상태로 이동하거나, 입자가 전멸될 때 생성되는 전자파이다. 인체나 살아있는 유기체가 오랫동안 노출되면 세포가 파괴되고 DNA의 변형을 유발할 수 있다. 세계보건기구 IARC(International Agency for Research on Cancer)가 지정한 그룹 1 발암물질이다[1].
감마선의 위험으로 인해 다양한 연구가 수행되고 있다. 이전에는 감마선의 인공 암종에 미치는 영향에 관한 연구가 수행되었지만, 최근에는 대표적인 천연 감마선인 라돈의 건강 효과에 관한 연구도 진행되고 있다[2]. 이처럼 감마선은 인공 및 천연 소재 모두에서 위험하므로 공간 감마선량 분석이 다양한 장소에서 수행되고 있다[3].
공간 감마선량과 기상 데이터는 대표적인 시계열 데이터에 대한 문제로 볼 수 있으며, 감마선량과 기상 데이터 간의 상관관계에 관한 연구를 통해, 감마선량은 일부 기상 데이터와 상관관계가 나타나고 있다[4].
시계열 데이터의 경우 LSTM 모델이 다른 기계 학습 모델보다 더 나은 성능을 보이는 경향이 있음을 나타낸다[5][6]. 그러나 LSTM 머신 러닝 모델의 주요 단점은 높은 계산 용량이 필요하므로 예측 프로세스의 실행 시간이 매우 오래 걸린다. 시계열 데이터의 예측 프로세스의 실행 시간을 줄이기 위해서, 자기 회귀(Auto Regressive)나 HMM(Hidden Markov Model)을 사용한 모델이 더 낮은 평균 제곱 오차로 나은 예측 정확도를 달성했음을 보여주고 있다[7].
본 논문에서는 공공데이터 포털(data.go.kr)에서 제공하는, 원자력발전소의 실시간 주변 방사선량과 실시간 기상정보 데이터를 활용하여 주기성 배제, 정규화 등의 전처리를 수행하고, 단변량 데이터로부터 ARIMA(Auto Regressive Integrated Moving Average) 모델을 구성하여 모델의 성능을 확인하고, VAR(Vector Auto Regression) 모델을 사용, 다변량 시계열 데이터로 확장하여, 다변량 시계열의 상호 의존성을 분석하였다. 이를 통해, VAR 다변량 시계열 데이터 예측 모델을 통해 기상 변화에 따른 공간 감마선량의 이상 상황 예측이 가능함을 보인다.
논문의 구성은 2장에서는 관련 연구로 ARIMA 모델, VAR 모델 그리고 이상 상황 예측 방법에 대해 살펴보고, 3장에서는 데이터 전처리 방법에 관해 설명한다. 4장에서는 단변량 데이터를 통해 모델을 구성하고 성능을 확인하는 과정 그리고 다변량 데이터를 통해 이상 상황 예측이 가능함을 보이고, 5장에서 결론을 맺는다.
Ⅱ. 관련 연구
2-1 ARIMA 모델
ARIMA 모델은 시계열 데이터에 대해, 자기 회귀, 통합 및 이동 평균을 이용하여 예측이 이루어지며, 여러 연구를 통해 단기간 데이터에 대해 불확실성 시계열 데이터를 예측하는 데 우수한 성능을 보였다[8][9]. ARIMA 모델은 식 1형태의 모형으로 표현한다. 자기회귀모형의 차수 p, 차분의 정도 d, 이동평균모형의 차수 q 일 때, ϕ(B)는 차수가 p인 B의 다항식이고, θ(B)는 차수가 q인 B의 다항식으로 각각 식 2, 식 3으로 정의된다.
| (1) |
| (2) |
| (3) |
2-2 VAR(Vector Auto Regression) 모델
ARIMA 분석 결과를 다변량으로 일반화하기 위해, 자기회귀 다변량 확장 모델인 벡터자기회귀(VAR) 모델을 사용하여, 다변량 시계열 데이터로부터 상관 패턴을 추출, 선형관계를 통해 단변량 자기회귀(AR) 모델을 확장한다[10]. 각 입력 시리즈에 대해 회귀를 수행하여 자기회귀 효과를 확인하고, 서로 다른 변수 간의 회귀를 수행하여 교차 지연효과를 확인한다.
시계열 상관관계가 있는 다변량 시스템에서 VAR 모델을 사용하여 시스템을 모델링하고 잔차의 독립성 확인을 통해 VAR 모형의 적합도를 판단 할 수 있다.
벡터자기회귀(VAR) 모형은 관심 있는 변수 시스템 간의 관계를 이해하기 위해 개발되었으며, 상호 간에 인과관계가 있는 k개의 시계열로 구성된 벡터 Zt가 p 시차인 자기회귀모형으로 구성된 다변량 시계열 모형을 VAR(p) 형이라고 하며 식 4와 같이 정의된다[11].
| (4) |
여기서 Zt는 k×1 시계열 벡터이며, δ는 k×1 상수 벡터, Φi(i = 1,2,⋯,p)는 k×k의 계수행렬, ϵt는 k×1의 백색잡음 과정의 벡터다. 또한 , 는 양정치 행렬이고 이다.
VAR(p) 모형의 시차 p는 일반적으로 AIC (Akaike’s information criterion) 통계치가 최소가 되는 값을 선택한다. 본 연구의 자료 분석에서 사용된 AIC는 식 5와 같이 정의된다.
| (5) |
여기서 r은 추정해야 할 모수의 수, n은 관찰치 수, 그리고 는 Σ의 최우 추정량이다.
ARIMA의 다변량 확장 모델인 VAR 모델(식 4)을 사용하여, 시계열 데이터로부터 상관관계 패턴을 추출하고, VAR에 의해 학습된 정보는 특정 지표(metric)가 임계값을 초과할 때 경고를 표시하는 임계값 메커니즘을 구축하는 데 사용된다.
2-3 이상 상황 식별(Hoteling T2)
호텔링의 T2 통계량 [12][13] 을 사용한 이 단계 관리도(phase II control chart)는 연속형 다변량 품질 특성치의 평균벡터를 온라인 모니터링할 때 자주 사용된다[14]. 이 관리도는 시점에 따라 관측된 통계량의 값으로부터 평균벡터의 변화 여부를 검정할 수 있도록 하는데, 관리한계선 내에서 통계량의 값이 관측되면 관리상태 즉 평균벡터의 변화가 없다고 판단하고, 관리한계선 밖에서 관측될 때는 그 시점에서 평균벡터 변화의 신호 즉 이상 신호가 발생했다고 해석한다.
p변량 데이터 는 관리상태 아래에서 평균벡터가 이고, 공분산 행렬이 Σ = (σij)p×p인 다변량 정규분포를 따른다고 가정한다. 일반적으로 μ와 Σ는 미지의 값이므로 관리상태 아래의 m개의 데이터 로 부터 와 로 추정된다. 이를 바탕으로 새로운 관측치 로부터 평균벡터의 변화를 온라인 모니터링하기 위한 호텔링의 T2 관리 통계량은 다음과 같이 정의되고 관리상태 아래에서 이 통계량은 자유도가 p이고 유의 수준이 알파α인 F 분포를 따르게 된다(식 6).
| (6) |
따라서, 위 통계량으로부터 다변량 관측치를 모니터링하기 위해 관리 상한선(upper control limit, UCL)을 식 7로 두고 평균벡터의 변화 여부를 판단하게 된다.
| (7) |
Ⅲ. 데이터 전처리
3-1 실험 데이터 세트
본 논문에서 이용한 데이터세트는 한국수력원자력(주) 원자력발전소의 실시간 주변 방사선량과 실시간 기상정보 공공데이터이다[15][16].
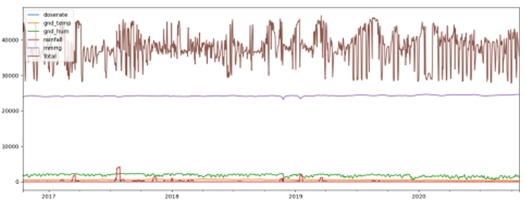
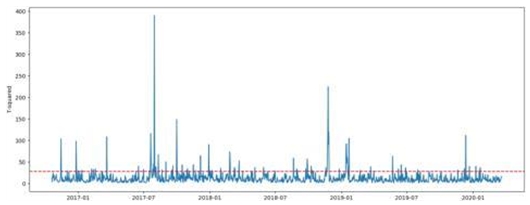
기상관측 데이터와 공간 감마 선량률 간의 상관관계를 파악하기 위하여, 2016년 10월부터 2020년 10월까지의 데이터를 사용하였다. 이 기간에 1시간 평균 공간 감마 선량 데이터, 1시간 평균 기상 측정 데이터를 (35,424 데이터)가 이용되었다. 실험에 사용된 데이터 리스트의 단위는 표 1과 같고 데이터 리스트와 합계(total)를 구하여 그림 1에 표시하였다.
이 데이터를 활용하여, 벡터자기회귀 기반 이상 상황(anomaly)을 예측하기 위해서 주기성 배제, 정규화 등의 전처리를 수행한다.
Ⅳ. 벡터자기회귀 이상 상황 예측
4-1 단변량 감마선량 이상 상황 예측
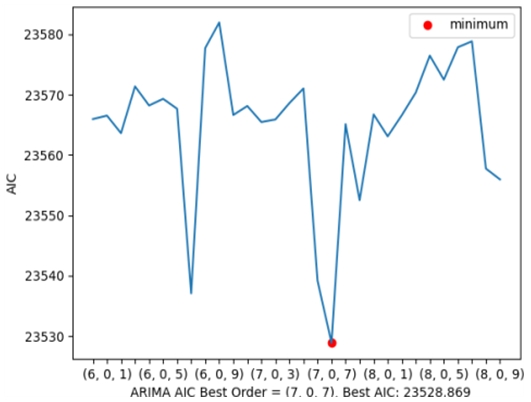
준비된 훈련데이터로부터 최적의 단변량 모델을 구하기 위해서는, AIC(Akaike’s information criterion)를 최소화하는 것이 필요하다. 학습 결과 AIC를 최소로 하는 시차 p는 7로 시계열 데이터에서 시차 7을 사용하여 자기회귀에 사용하도록 하였다(그림 3).
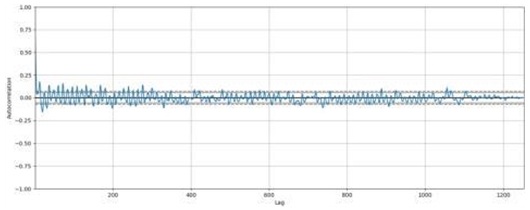
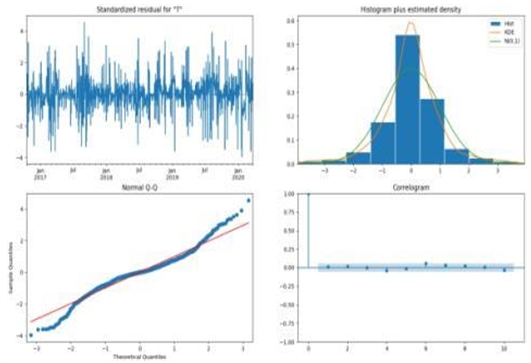
구해진 단변량 모델은 자기상관(correlogram) 정도가 없는 정규 잔차를 생성하는 것으로 판단된다. Q-Q 플롯도 직선의 형태로 잔차의 정규성을 따르는 것으로 보인다(그림 4).
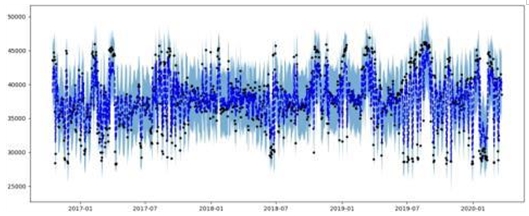
그림 5는 단변량 훈련데이터에 대하여 ARIMA 학습에 따른 예측값과 90% 신뢰구간(alpha=0.1)을 나타낸 것이다.
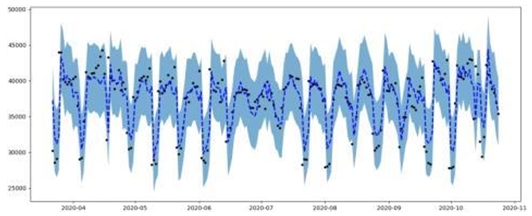
그림 6은 훈련데이터를 통해 구한 단변량 모델을 테스트 테이터에 적용하여, ARIMA 학습에 따른 예측값과 90% 신뢰구간(alpha=0.1)을 나타낸 것이다.
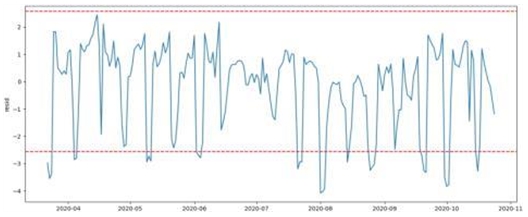
ARIMA 예측을 통해, 잔차가 90% 신뢰구간을 벗어나는 경우와 그 잔차의 크기를 통해 이상 상황을 판단할 수 있다. 그림 7은 훈련데이터로부터 구한 잔차로, 상한(5%)과 하한(5%)의 범위를 넘는 경우 그리고 그 잔차의 크기가 큰 경우가 이상 상황으로 볼 수 있다.
4-2 다변량 감마선량 이상 상황 예측
ARIMA 분석 결과를 다변량으로 일반화하기 위해, 벡터자기회귀(VAR) 모델을 사용하여, 다변량 시계열 데이터로부터 상관 패턴을 추출, 선형관계를 통해 단변량 자기회귀(AR) 모델을 확장한다.
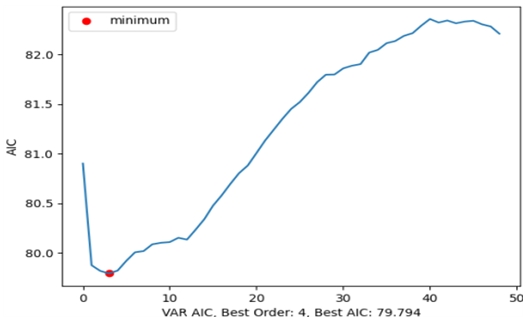
최적의 다변량 모델을 구하기 위해서는, AIC를 최소화하는 것이 필요하다. 학습 결과 AIC를 최소로 하는 시차 p는 4로 시계열 데이터에서 시차 4를 사용하여 자기회귀에 사용하였다(그림 8).
2017년 1월부터 2020년 2월까지의 훈련 테이터에 대해 최적 다변량 모델(VAR)로부터 잔차(residual)를 구한 다음, 호텔링 T2값과 UCL을 구하여 그림 9에 나타내었다. UCL 이상 표시되는 호텔링 T2값을 통해 이상 상황(anomaly)으로 판정할 수 있다.
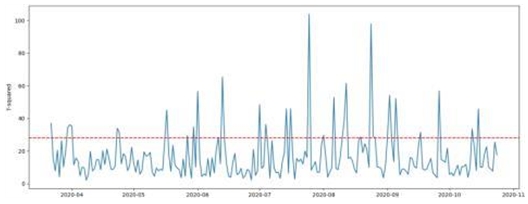
그림 9에서 훈련데이터에 대해 T2값과 UCL을 구하여 이상 상황(anomaly)으로 예측하는 것이 가능해 짐에 따라 테스트 테이터에 대해 적용한다. 2020년 3월부터 2020년 10월까지의 테스트 테이터와 이전 훈련데이터를 통해 생성한 모델로부터의 테스트 테이터의 예측값과의 차이인 잔차(residual)를 구한 다음, 호텔링 T2값과 UCL을 구하여 그림 10에 나타내었다. 그림10을 통해 UCL 이상 표시되는 호텔링 T2값이 이상 상황(anomaly)으로 판정할 수 있다.
Ⅴ. 결 론
실시간 주변 방사선량과 실시간 기상정보 공공데이터를 토대로 감마선량의 이상 상황을 예측하기 위하여 ARIMA(Auto-regressive Integrated Moving Average) 모델을 사용하였다. ARIMA 모델은 시계열분석에서 널리 사용되고 있으며, 자동회귀이동평균 모델을 일반화한, 자동회귀누적이동평균 모델로 시계열 데이터를 더 잘 이해하거나 미래 지점을 예상하기에 적합하다.
ARIMA를 이용하여 단변량(univariate) 이상 탐지 접근 방식 사용하여, 데이터세트를 훈련 세트와 테스트 세트로 구분하였고 장기 주기성을 제거한 다음, AIC(Akaike Information Criterion) 기준을 통해 최적합 모델을 선택하였으며, 테스트 세트에 적용하여 신뢰구간을 벗어난 잔차를 통해 이상 상황 식별이 가능함을 보였다. 이어서, 모든 계열의 상호 작용을 고려한, 벡터자기회귀(VAR) 모델을 사용하여 다변량 분석(multivariate)에 적용하여, VAR 잔차를 통해 임계값을 넘는 이상 상황인 경우 경고를 하는 시스템 제작이 가능함을 확인하였다.
이번 연구를 통해 적절한 데이터 선택과 단변량 이상 탐지를 기반으로 다변량 이상 탐지가 가능함을 제시하였고, 이 기술을 활용하여 공공데이터와 기상 데이터를 토대로 감마선량의 이상 상황 예측 가능성을 더욱 높일 수 있음을 확인하였다.
References
- IARC, “Ionizing radiation, Part 1: X- and gamma-radiation and neutrons,” IARC Monogr Eval Carcinog Risks Hum, Vol. 75 pp. 1-492, PMID:11203346, 2000.
-
N. Syam, “Determination of radon leakage from sample container for gamma spectrometry measurement of 226Ra,” Journal of Environmental Radioactivity, Vol. 220-221, 2020.
[https://doi.org/10.1016/j.jenvrad.2020.106275]

-
J. Amestoy, “Impacts of gamma radiation, as hygiene physical control agent, on population growth of Tribolium castaneum in wheat flour,” Journal of Radiation Research and Applied Sciences, Vol. 15, Issue 1, pp. 179-186, 2022.
[https://doi.org/10.1016/j.jrras.2022.03.001]

-
R. M. Tabikha, “Effects of environmental factors on the monitoring of environmental radioactivity by airborne gamma-ray spectrometry,” Journal of Environmental Radioactivity, Vol. 237, 2021.
[https://doi.org/10.1016/j.jenvrad.2021.106695]

-
Tandon, “Bitcoin Price Forecasting using LSTM and 10-Fold Cross validation,” International Conference on Signal Processing and Communication (ICSC), Noida, India, March 7-9, 2019.
[https://doi.org/10.1109/ICSC45622.2019.8938251]

-
K. Kwon, “Forecast of Bee Swarming using Data Fusion and LSTM”, Journal of Digital Contents Society, Vol. 20, pp. 1-6, 2019.
[https://doi.org/10.9728/dcs.2019.20.1.1]

-
Hashish, “A Hybrid Model for Bitcoin Prices Prediction using Hidden Markov Models and Optimized LSTM Networks,” 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, September 10-13, 2019.
[https://doi.org/10.1109/ETFA.2019.8869094]

-
Ariyo, “Stock Price Prediction Using the ARIMA Model,” 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, March 26-28, 2014.
[https://doi.org/10.1109/UKSim.2014.67]

-
Roy, “Bitcoin Price Forecasting Using Time Series Analysis,” 21st International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, December 21-23, 2018.
[https://doi.org/10.1109/ICCITECHN.2018.8631923]

-
Sims, “Macroeconomics and reality,” Econometrica: Journal of the Econometric Society, Vol. 48, pp. 1-49, 1980.
[https://doi.org/10.2307/1912017]

- Sims, “A Nine-Variable Probabilistic Macroeconomic Forecasting Model,” In Business Cycles, Indicators and Forecasting. Chicago: University of Chicago Press, pp. 179-212, 1993.
- Hotelling, “Multivariate Quality Control, Techniques of Statistical Analysis,“ Eisenhart, Hastay, and Wallis (eds), McGraw-Hill, New York, 1947.
- Sungim Lee, “Identification of the Out-of-Control Variable based on Hotelling’s T2 Statistic,” The Korean Journal of Applied Statistics, Vol.31 pp.811-823, 2018.
-
Lim, J. and Lee, S., “Phase II monitoring of changes in mean from high-dimensional data,” Applied Stochastic Models in Business and Industry, Vol. 33, pp. 626-639, 2017.
[https://doi.org/10.1002/asmb.2267]

- KNHP, Real-time Ambient Radiation Dose of Korea Hydro & Nuclear Power Co., Ltd., Available: https://www.data.go.kr/data/15001081/openapi.do, , 2020.
- KNHP, Real Time Weather Information of Korea Hydro & Nuclear Power Co., Ltd., Available: https://www.data.go.kr/data/15001091/openapi.do, , 2020.
저자소개

1993년 : 강원대학교 컴퓨터과학과(학사)
1995년 : 강원대학교 대학원 컴퓨터과학과(석사)
2000년 : 강원대학교 대학원 컴퓨터과학과(박사)
1998년~2002년: 동원대학 인터넷정보과 교수
2002년~현 재: 강원대학교 정보통신공학과 교수
※관심분야:패턴 인식 (Pattern Recognition), 사물 인터넷 (IoT), 기계학습

1984년 : 서울대학교 계산통계학과(학사)
1986년 : 서울대학교 대학원 계산통계학과(석사)
2000년 : 강원대학교 대학원 컴퓨터과학과(박사)
1986년~1994년: LG전자 컴퓨터연구소
1994년~1999년: 한국디지털(주)
2004년~현 재: 강릉원주대학교 컴퓨터공학과 교수
※관심분야:무선 통신 (Wireless Networks), 센서 네트워크 (Sensor Networks), 임베디드 시스템 (Embedded Systems), 사물 인터넷 (IoT)