ARM과 MSMM을 활용한 지식 그래프의 선후관계 분석 : K-12 수학 문항 평가 데이터를 중심으로
Copyright ⓒ 2022 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
본 연구는 ARM과 MSMM 방식을 적용하여 지식 그래프의 지식 요소(KC) 간 선후 관계를 도출하는 RCA 분석 프로세스를 제안하고 초중등 레벨의 수학 문항 평가 데이터에 적용하여 그 결과를 분석하였다. 이는 조건부 확률의 개념을 서로 다른 통계량으로 보여주는 여러 방법을 혼합하여 활용하였다는 데에 의미가 있으며 시차를 고려한 학습 데이터에 MSMM 방식을 적용함으로써 선후 관계 분석의 일치도(precision)를 높일 수 있음을 보였다. 본 연구에서 제안한 ARM+MSMM을 활용한 KC 간 선후관계 분석 모델은 학습자 데이터에 기반하여 교육 과정 속 지식 요소의 선후관계를 검증하고 숨겨진 지식 요소 관계를 추가로 제시함으로써 지식 그래프를 강화하는 데에 기여할 수 있을 것이다.
Abstract
This study proposes the RCA analysis process using the ARM and MSMM methods for deriving prerequisite relation between knowledge components(KC) of a knowledge graph and analyzed the results by applying it to elementary and middle school level math item evaluation data. This is meaningful in that the proposed process combines several methods that show the concept of conditional probability with different statistics, and the precision of the prerequsite relation analysis was increased by applying the MSMM method to the learning data considering the disparity. The prerequisite relation analysis model between KCs using ARM+MSMM proposed in this study can strengthen the knowledge graph by verifying the relationship of knowledge component in the curriculum based on learner data and contribute to additional suggesting hidden knowledge component relationships.
Keywords:
Prerequisite Relation, Knowledge Graph, Association Rule Mining, Multi-State Markov Model, Root Cause Analysis키워드:
선후관계, 지식그래프Ⅰ. 서 론
4차 산업혁명 시대를 맞이하여 급변하는 산업 변화에 적응하기 위해 누구나 원하는 시점에 필요한 지식을 습득하고 활용하는 평생학습이 강조되고 있다. 또한, 최근 예기치 않게 팬데믹 상황이 장기화하면서 청소년들에게 안정적인 정규 교육을 제공하기 위해 온라인 학습 환경에 대한 요구가 증가하고 있다. 이에 대해 유명 대학의 강의를 언제 어디서나 온라인으로 수강할 수 있도록 공개하는 MOOC(massive open online course)와 같은 교육 플랫폼은 좋은 해법이 될 수 있다[1]. MOOC 플랫폼은 학습자가 원하는 시점에 필요한 강의를 선택하여 학습할 수 있는 범위를 확장했다는 점에서 교육 패러다임을 혁신하는 계기를 제공했다. 이와 같은 MOOC 플랫폼의 장점에도 불구하고 학습자의 동기 부여와 자기 주도적 학습 태도, 문화적 배경, 지적 수준에 따라 MOOC 강좌에 대한 수용도에 차이가 있다고 알려져 있다[2]-[3]. 서명훈[4]은 MOOC를 이용하는 학습자의 동기에 영향을 미치는 주요 요인으로 모바일 학습 환경과 같은 촉진 조건, 학습 효율성에 대한 성과 기대, 사회적 영향이 있다고 분석하였으며, 김세영[5]과 이지연[6]은 온라인 학습 상황에서는 교수자와 학습자 간의 소통이 제한적이기 때문에 학습과 평가 과정에서 피드백을 즉각적으로 전달하기 어려운 점을 지적하였다.
MOOC 플랫폼을 포함한 온라인 학습 환경에서 발견되는 제한점을 극복하기 위해 컴퓨팅 기술을 활용한 개인화 학습(personalized learning)을 고려할 수 있다[7][8]. 개인화 학습은 학습자 개인의 사전 경험, 지식, 학습 패턴 등의 특성에 따라 맞춤형 학습 속도와 방법을 제시하는 방식이다. 특히 빅데이터와 인공지능 기술을 활용하여 대량의 교육 데이터를 실시간으로 분석한 결과를 바탕으로 최적의 학습 경로(learning path)를 자동으로 추천하거나 피드백을 제공하는 적응형 학습(adaptive learning) 방식을 통해 높은 수준의 개인화 학습을 구현할 수 있게 되었다[9][10].
적응형 학습의 핵심 요소인 학습 경로는 교육 과정에서 습득해야 하는 지식 요소(knowledge component)와 이들의 관계로 표현된 지식 그래프(knowledge graph)로부터 도출된다. 이 지식 그래프를 기반으로 학습자의 지식 습득 수준을 추적(knowledge tracing)하거나 맞춤형 학습 경로를 추천할 수 있는 모델을 구축할 수 있다[11]. 통상적으로 지식 그래프의 원형은 교육전문가 혹은 교수자에 의해 교육 과정에 맞게 정의되어 왔으나 최근에는 인공지능 기술을 이용하여 다양한 유형의 교육 콘텐츠를 분석하여 지식 요소를 추출하고 그 선후관계를 모델링하는 연구가 진행되고 있다. Liangming Pan 등[12]은 광범위한 온라인 교육 과정을 제공하는 MOOC에서 지식 요소 간 선후관계의 추론에 영향을 주는 데이터셋을 제시하였다. Zhou 등[13]은 교육 데이터로부터 지식 요소를 추출하고 이들 사이의 선후관계를 추출하는 방법론을 제안하였다. 학습자의 지식을 모델링하는 기법으로 잘 알려진 BKT(bayesian knowledge tracing)는 학습자의 문항 반응을 이해와 비이해의 두 개의 상태로 두고 베이지안 기반 확률 추정을 사용한다[14]. BKT는 학습자의 지식 상태를 문항 테스트 결과에 의해 두 경우로만 매칭하는 한계가 있다. 이에 RNN(recurrent neural networks)을 활용한 딥러닝을 적용하여 학습자의 지식을 모델링하는 DKT(deep knowledge tracing) 기법이 등장하였고[15], 나아가 지식 요소의 선후관계를 반영하거나[16] 문맥상 예측[17], 난이도 수준을 적용[18]하도록 DKT를 확장한 기법들이 제안되었다.
Chen 등[19]은 교육 콘텐츠로부터 지식 요소를 자동으로 추출한 후 학습자의 학습 결과를 확률적으로 분석하여 지식 요소 간 관계를 도출하고 해당 교육 과정의 지식 그래프를 생성하는 KnowEdu 시스템을 제안하였다. KnowEdu는 교육 콘텐츠로부터 교육 과정의 지식 그래프를 자동으로 생성하는 체계를 구축했다는 점에서 의의가 있다. 그러나 지식 요소 간 선후관계를 분석할 때 학습 시점에 따른 영향을 고려하지 않았다는 한계가 있다.
본 연구에서는 학습 활동의 시차에 따른 학습자의 성취 수준의 변화를 기반으로 지식 요소 간 선후관계를 분석하는 프로세스를 제안하였다. 우선 학습 데이터에 연관성 분석(ARM, association rule mining) 기법을 적용하여 유의미한 관계를 보이는 지식 요소의 쌍을 선별한다. 다음으로 ARM 분석에 의해 도출된 지식 요소 관계들에 해당하는 문항 평가를 2회 진행한 학습 데이터에 대해 MSMM(multi-state markov model) 방식을 적용하여 유의미한 선후관계를 도출한다. 이와 같은 ARM+MSMM 알고리즘을 K-12 수학 과정의 학습 데이터에 적용하여 도출한 지식 요소의 선후관계는 타겟 선후관계와 평균적으로 약 50% 일치하는 것을 확인하였다. 이는 ARM 기법만 적용했을 때와 비교하여 일치도가 약 2배 가량 개선된 결과이다. 따라서 학습자가 같은 문항 세트를 여러 회차에서 풀어낸 결과로부터 학습 시차를 고려한 MSMM 방식을 적용함으로써 선후 관계 분석의 일치도(precision)를 높일 수 있음을 확인하였다. 한편 MSMM을 적용하여 도출한 선후관계 목록은 실제 학습 데이터를 반영한 것이므로 타겟 KC 선후관계와 일치하지 않은 항목 중에서 실질적으로 학습 효과에 영향을 주는 선후 개념이 발견될 수 있다.
따라서 본 연구에서 제안한 ARM+MSMM을 활용한 KC 간 선후관계 분석 모델은 학습자 데이터에 기반하여 해당 교육 과정에서 습득해야 하는 지식 요소의 선후관계를 검증하고 더 나아가 숨겨져 있던 지식 요소의 관계를 추가로 제시함으로써 교육 과정을 표현한 지식 그래프를 강화하여 적응형 학습을 실현하는 데에 기여할 수 있을 것으로 기대된다.
Ⅱ. 이론적 배경
2-1 근본원인분석 (RCA, root cause analysis)
학습 과정 중 특정 지식의 습득에 어려움이 있다면 그 원인을 면밀하게 분석해야 한다. 이렇듯 문제가 발생했을 때 그 문제를 발생하게 한 원인을 찾아서 제거하는 분석 방법을 근본원인분석(이하 RCA)라고 한다. 널리 알려진 RCA는 피쉬본 다이어그램(fish bone diagram)을 활용하여 문제의 원인을 확인하는 절차를 따른다[20]. 나아가 문제 발생에 영향을 미치는 원인을 찾기 위해 관련 데이터로부터 현재의 문제 상태를 종합적으로 분석할 수 있는 컴퓨팅 기술과 도구를 넓은 의미의 RCA라고 할 수 있다.
RCA 중에서 어떤 문제를 일으키는 원인의 불확실성을 고려하지 않는 방식을 결정적(deterministic) RCA라고 한다. 결정적 RCA의 예로 원인의 설명이 가능한 의사결정트리(decision tree), 원인을 설명하기는 불가능하나 예측된 값을 확인할 수 있는 신경망(neural net) 알고리즘 등이 있다. 한편, 현재의 상태에서 직전의 상태 또는 영향 요인의 불확실성을 고려한 원인분석 모델을 확률적(probabilistic) RCA라고 한다. M Solé[21]은 결정적 RCA와 확률적 RCA의 대표적 구현 기법을 표 1과 같이 제시하였다.
2-2 지식 요소의 선후관계
학습자가 어떤 개념을 이해하기 위해 반드시 먼저 습득해야 할 개념이 있다면 두 개념 사이에 선후관계(prerequisite relation)가 존재한다고 할 수 있다. 가령 초등 수학에서 곱셈은 덧셈을 먼저 습득해야 이해할 수 있으므로 덧셈 개념과 곱셈 개념은 선후관계가 있다. 모든 교육 과정에는 해당 분야의 교육전문가들에 의해 지식의 선후관계가 반영되어 있다. 칸 아카데미(Khan Academy)와 같은 온라인 학습 시스템[22]에는 지식 개념의 선후관계를 지식 그래프(knowledge graph) 형태의 데이터로 표현하여 학습자 맞춤형 서비스에 반영한다[23]. 최근에는 학습 교재나 멀티미디어 교육자료에서 추출한 지식 요소 정보를 이용하여 자동으로 지식 그래프를 생성하는 연구가 진행되고 있다[15],[19].
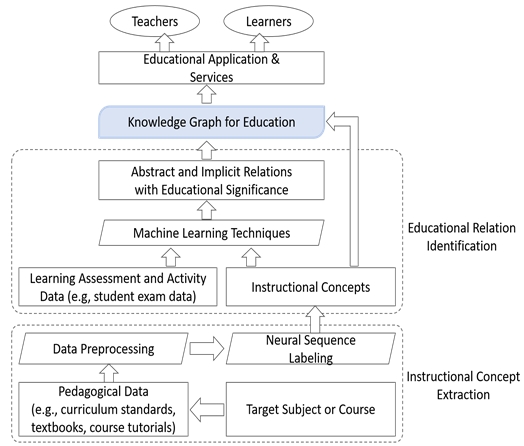
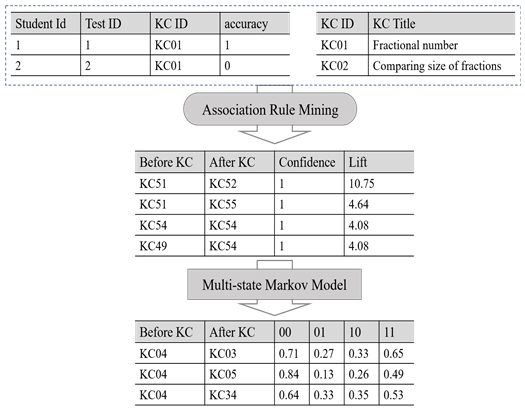
Chen 등[19]은 그림1에 명시된 바와 같이 지식 컨셉 추출(instructional concept extraction) 단계에서 교과서, 교육 자료 등을 디지털 데이터로 변환한 후 이로부터 주요 컨셉을 추출한다. 이렇게 추출된 컨셉의 습득(mastery) 여부를 1과 0으로 표현한 학습 평가 데이터셋에 ARM을 적용하여 컨셉 간 선후관계를 도출한다. 가령, 컨셉 추출 단계에서 컨셉 A, B를 도출했다면 해당 컨셉들의 학습 평가 데이터셋에 식(1)의 조건부 확률값을 얻는다.
| (1) |
이 조건부 확률값이 미리 정한 신뢰도(confidence)와 지지도(support)를 만족하면 컨셉 A와 컨셉 B 사이에 선후관계 A→B가 성립한다고 판단한다.
2-3 ARM (association rule mining)
ARM은 주어진 데이터로부터 어떤 사건들이 서로 연관되어 나타나는지를 연관 규칙(association rule)으로 표시하는 데이터 마이닝 알고리즘이다. 데이터 마이닝에 의해 추출된 연관 규칙은 지지도(support), 신뢰도(confidence), 상승도(lift)의 척도로 나타낸다.
| (2) |
| (3) |
| (4) |
이 중 상승도를 이용하여 연관 규칙의 중요도를 평가할 수 있을 뿐 아니라 표준화를 통하여 그룹 간 비교도 가능하다. 그러나 주변 사건 중 ARM을 수행하기 위해 미리 결정된 신뢰도와 지지도의 하한에 만족하는 규칙만 찾을 수 있다는 단점이 있다. 이를 보완하기 위해 MSMM을 고려해볼 수 있다.
2-4 MSMM (multi-state markov model)
MSMM은 시간을 고려한 Marcov Model을 통하여 관측치가 가질 수 있는 여러 개의 상태를 예측할 수 있는 모델이다. MSMM은 ARM과 달리 관측치의 모든 경우의 수에 대한 확률값을 한꺼번에 보여준다는 장점이 있다. 상태의 변화에는 시차와 영향을 주는 요인들의 특성이 영향을 미치게 된다. Kalbfleisch 등[24]은 시간을 연속적인 값을 가지는 것으로 가정하고, MSMM에서 상태 간 전이확률을 최대 우도 추정 방법으로 예측하는 방법을 제시하였다.
M. Hill 등[25]에 따르면, Y(t), t ≥ 0를 유한한 상태 공간 Z = 1,...,Z에 정의된 stochastic process라 하고 시간 s(0 ≤ u ≤ s)까지의 정보인 HS가 알려져 있다고 할 때, 임의의 시간 s에서의 상태를 a라고 하면 s < t 인 t 에 대해 Y(t)가 상태 b에 있을 확률은 식(5)와 같이 정의된다.
| (5) |
식(5)는 markov property에 따라 식(6)과 같이 정리할 수 있다.
| (6) |
상태 a에서 상태 b로의 전이확률을 Pab(s,t)라 할 때, 미세한 시간 구간 사이의 전이확률을 모두 합하는 것이라고 한다면 전이확률 Pab(t)은 식(7)과 같이 정의할 수 있다.
| (7) |
이를 상태 a에서 b로 가는 상태, 특정 상태에서 머무르는 기간의 기대치eab(s,t)로 해석하면 식(8)과 같게 된다.
| (8) |
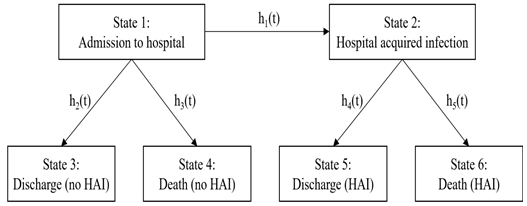
M Hill 등[25]은 MSMM 기법을 이용하여 병원 감염과 관련하여 6개의 관심 상태에 대해 전이확률과 각 상태에 머무르는 기간을 추정하였다. 그림 2는 환자의 병원 입원, 원내감염, 퇴원, 사망의 프로세스를 나타낸 MSMM 모델로 h1(t)~h5(t)는 상태 전이에 따른 요구 시간을 의미한다.
Ⅲ. 연구 설계
본 연구에서는 실질적으로 학습 효과에 영향을 주는 지식 요소(knowledge component, KC) 간 선후관계를 도출하기 위해 주어진 지식 그래프와 학습자의 평가 데이터를 바탕으로 ARM과 MSMM 방식을 혼합 적용한 모델을 제안한다.
3-1 KC 간 선후관계 분석 알고리즘의 설계
KC A에 대해 학습자의 습득 상태를 KC(A)라 하자. 학습자가 KC A를 모르는 상태, 즉 학습 평가에서 관련 문항에 오답을 제출한 경우 KC(A) = 0이라 정의하고, 학습자가 해당 문항에 정답을 제출했다면 아는 상태라 보고 KC(A) = 1로 정의한다.
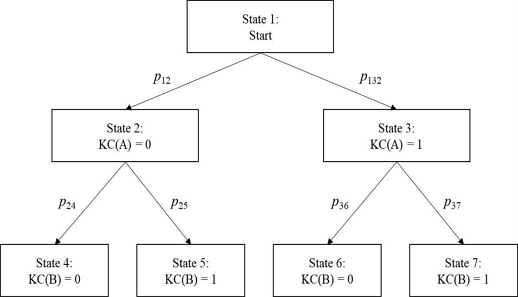
서로 다른 KC A와 B에 대해 KC(A)가 모르는 상태에서 아는 상태로 전이하는 사건과 KC(A)의 정·오답 상태가 KC(B)의 정·오답 상태에 영향을 미치는 사건은 모두 시차에 의존적이다. 그림 3은 KC(A)와 KC(B) 간에 발생할 수 있는 모든 상태 전이의 경우를 도식화한 것이다. 그림 3에서 각 상자의 왼쪽에 표기된 숫자는 각 상태의 식별 번호이며 Pab는 상태 a로부터 상태 b로 전이할 확률을 나타낸다.
본 연구에서는 KC 간 상태 전이와 관련하여 시간에 따라 변화하는 사건들은 markov process을 따르는 것으로 가정한다. 각 KC의 상태가 여러 개의 값을 가지게 되므로 다중상태를 분석할 수 있는 MSMM(multi-state markov model)을 적용하여 KC의 선후관계를 추정할 수 있다. 즉, 2회 이상의 시계열 측정이 이루어진 학습 데이터에 MSMM을 적용하여 선후관계가 있는 KC 목록을 얻을 수 있다.
그런데 MSMM은 KC 간 선후관계가 지닌 상승도(lift) 혹은 전체 모집단 중에 관심 사건이 발생하는 확률과 같은 통계량을 제공하지 않는다. 이와 같은 MSMM의 약점을 보완하기 위해 본 연구에서는 학습 데이터에 ARM 기법을 적용하여 통계적으로 유의미한 KC 관계 목록을 먼저 도출한 후 이를 대상으로 MSMM을 적용하는 것으로 설계하였다.
즉, KC 간 선후관계가 미리 정해진 충분한 지지도를 만족한다는 가정 아래 ARM 방식에 따라 식(9)와 식(10)에 의해 신뢰도 α를 만족하는 KC(A)와 KC(B)로부터 KC 관계 KCA → KCB의 항목을 얻는다.
| (9) |
| (10) |
ARM 분석에 의해 얻은 KC 관계 목록을 식(11)과 식(12)에 의해 MSMM 방식으로 정제한다.
| (11) |
| (12) |
MSMM은 시간 정보를 사용하기도 하지만 계산에 사용하는 확률값들이 최대 우도 추정치라는 점에서 ARM과 차이가 있다. ARM은 첫 번째 시험 로그 데이터를 조건부 확률 정보만으로 계산하므로 시간 정보를 이용하지 않지만 MSMM에서는 두 번째 치른 시험 데이터 내에서 KC의 풀이 순서에 따라 시차를 고려할 수 있으므로 모형화가 가능하다.
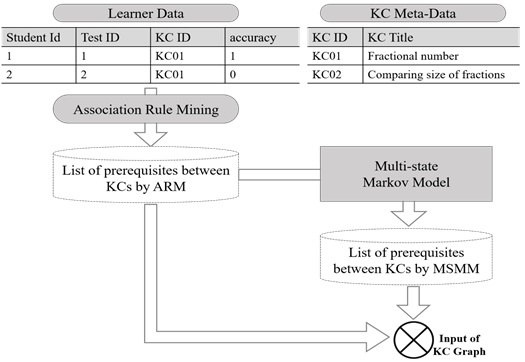
본 연구에서 설계한 KC 간 선후 관계를 도출하기 위해 설계한 ARM+MSMM 분석 과정을 그림 4에 나타내었다. 정제된 학습 로그 데이터에 ARM을 적용하여 유의미한 KC 간 관계 목록 A를 얻어낸다. 다음으로 1차와 2차 학습 로그 데이터, 즉 2회의 시계열 데이터에 MSMM 방식을 적용하여 KC 간 선후관계 목록 M을 얻는다. 마지막으로 목록 A와 목록 M을 교차하여 최종적으로 KC간 선후관계 목록을 구성한다.
3-2 연구 데이터의 구성
ARM과 MSMM에 의한 KC 간 선후관계를 도출하기 위해 본 연구에서는 국내 초·중 학생을 대상으로 한 D사의 온라인 수학 학습 서비스를 통해 수집한 학습 데이터를 활용하였다. 즉, 레벨 10부터 레벨 13까지의 학습 과정을 이수한 학생들의 KC별 문제풀이 로그 데이터를 사용한다. 이때 KC는 각 레벨의 커리큘럼에서 추출된 항목을 기준으로 미리 정한다. D사의 수학 학습 서비스에서 교사는 학습자가 해당 레벨의 개념을 모르는 것으로 판단하면 동일한 문제를 3차까지 테스트하게 한다. 본 연구에서는 시차가 있는 학습 상태의 변화를 분석하기 위해 2차까지 학습한 로그 데이터를 사용하였다. 표 2는 본 연구에서 활용한 D사의 K-12 대상의 수학 학습 데이터의 레벨별 구성을 나타낸 것이다.
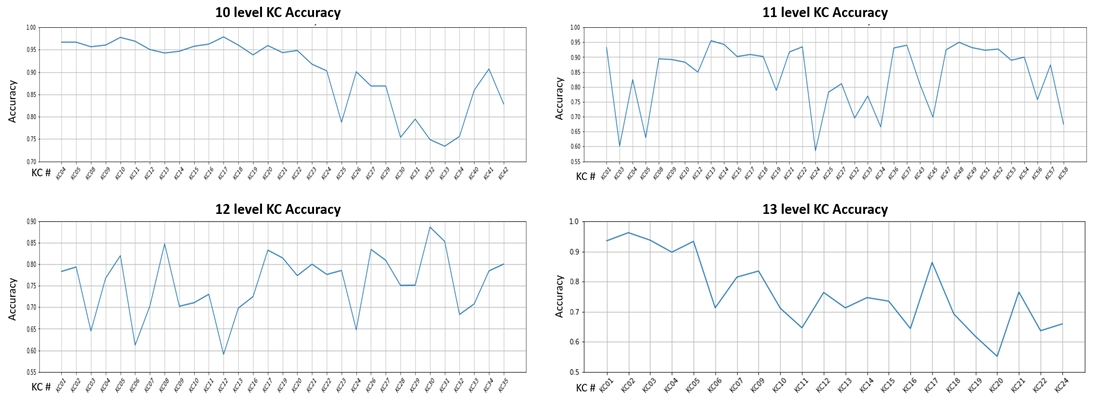
그림 5는 레벨 별로 KC별 평균 점수를 나타낸 그래프이다. 각 레벨 내에는 상대적으로 낮은 특이점을 보이는 KC 구간을 발견할 수 있는데 해당 KC가 다른 KC의 습득에 영향을 주는 선후관계가 존재할 가능성이 높다고 가정해 볼 수 있다.
그림 6에서 나타낸 바와 같이 D사의 학습 데이터를 서비스에 가입한 학생 아이디, 시험 회차, KC 식별자, 응답으로 재구성한 후 레벨별로 학습자별 1차 학습 데이터에 ARM을 적용하고 다음으로 같은 문제를 2회 학습한 학습자 데이터에 MSMM을 적용하여 선후관계 목록을 얻는다.
Ⅳ. 결과 및 분석
4-1 ARM을 이용한 KC간 관계 도출
그림 4의 분석 알고리즘 흐름에 따라 학습자의 응답 데이터를 기반으로 주어진 레벨의 모든 KC 간 관계에 대해 ARM을 적용하여 조건부 확률을 계산한다. 즉, 식(7)에 의해 KC(B)가 오답일 때 KC(A)가 오답일 조건부 확률이 신뢰도 α 및 지지도 β보다 큰 KC 관계를 대상으로 식(6)과 같이 KC(A)가 정답일 때 KC(B)가 정답일 조건부 확률이 동일하게 신뢰도 α 및 지지도 β를 만족하는 경우를 선별하여 유의미한 KC 관계 목록을 생성한다.
표 4는 D사의 온라인 수학 서비스에서 수집한 레벨 11의 학습 데이터에 ARM을 적용하여 얻은 KC 48의 관계 목록의 일부를 나타낸 것이다. 예를 들어, 표 4의 두 번째 행에서 KC 47과 KC 48의 관계에 대해 식(7)을 적용한 조건부 확률은 P(KC(47) = 0|KC(48) = 0) = 0.70으로 신뢰도(0.4)와 지지도(0.001)를 만족하므로 유의미한 관계 후보이다. 이 때 P(KC(48) = 1|KC(47) = 1)이 같은 신뢰도와 지지도를 만족한다면 KC 48 KC 47의 관계가 존재한다고 판단할 수 있다.
ARM을 1회 적용한 결과만으로는 신뢰도와 결과의 불확실성에 의문이 생길 수 있다. 예를 들어 표5의 KC08과 KC34의 관계는 두 개념 ‘자연수를 가분수로, 가분수를 자연수로 나타내기’와 ‘소수 사이의 관계’ 의 관련성을 이해하기 용이하지 않고, KC51과 KC52의 관계는 양방향으로 유의미한 신뢰도 수준을 보이므로 이에 대한 추가 확인이 필요하다.
4-2 ARM+MSMM을 이용한 KC간 선후관계 분석
본 연구에서는 1차 테스트에서 KC A에서 오답을 낸 학생들이 2차 테스트에서 KC A와 KC B에서 보이는 상태 변화를 고려함으로써 MSMM 분석 과정에 학습 시차를 반영한다. 이를 위해 앞서 ARM을 적용하여 도출한 KC 관계 목록에 대하여 테스트를 2회 진행한 학습자의 데이터를 추려서 MSMM 적용을 위한 학습 데이터를 준비한다.
MSMM 분석을 위해 개별 학습 데이터는 표 6과 같이 state를 정의한다. n차 테스트에서 KC A를 맞추었는지 혹은 못맞추었는지를 나타내는 상태값을 KCn (A)이라고 하자. 1차 테스트에서 KC1 (A) = 0을 시작 상태로 보고 본 연구의 MSMM모델의 state 1로 정의한다. 1차 테스트에서 KC A를 맞추지 못한 상태에서 2차 테스트의 KC A를 또 틀린 경우, 즉 KC2 (A) = 0인 상태를 state 2로 정의한다. 2차 테스트에서 KC A를 맞추지 못하고 KC B도 맞추지 못한 경우, 즉 KC2 (A) = 0인 상태에서 KC2 (B) = 0인 상태를 state 4로 정의한다. 이는 그림 3에서 KC 간 선후 관계 모델과 동일한 구조이다.
이제 ARM을 적용하여 도출한 각 관계의 KC A와 KC B에 대해서 우선 1차 테스트에서 KC A를 맞추지 못한 학습자들의 2차 테스트 학습 데이터에서 KC A와 KC B의 맞춤 여부에 따라 표 6과 같이 state를 할당한다.
표 6의 student id 항목은 학습자의 식별자, time order는 학습자가 해당 KC에 대한 테스트를 진행한 시점의 순서를 의미한다. state는 표 6에 나타낸 바와 같이 정의된 학습자의 학습 상태이다.
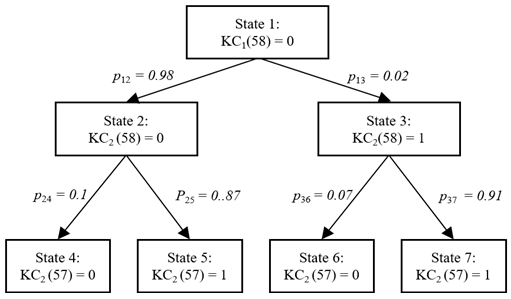
표 7에서 나타낸 바와 같이 KC A와 KC B가 표현할 수 있는 7개의 state와 그들 사이의 전이할 수 있는 확률을 상태 전이 다이어그램(state transition diagram)으로 표현할 수 있다. 그림 7은 레벨 11의 KC 58과 KC 57 사이의 상태 전이 다이어그램이다. 가령, 1회차 테스트에서 KC(58)이 오답인 상태에서 2회차 테스트에서 KC(58)이 오답일 확률 P12은 0.98이다. 2회차 테스트에서 KC(58)인 오답일 때 KC(57)이 정답일 확률 P25는 0.87이다.
ARM을 적용하여 얻은 KC 관계 목록의 모든 항목에 대해 2회차 테스트에서 수집한 학습 데이터를 기반으로 그림 7과 같은 상태 전이 확률을 구한 후 식(8)과 식(9)를 적용하여 MMSM 분석을 진행하였다. 표 8은 레벨 11에 MSMM을 적용하여 얻은 KC 간 선후관계 목록의 일부를 나타낸 것이다. 표 8에 의하면 KC04와 KC03의 관계에서, KC04를 틀릴 경우 KC03을 틀릴 확률 P24 이 0.71이고 KC04를 맞출 경우 KC03을 틀릴 확률이 P37 이 0.65이므로, KC 04 → KC 03 의 관계가 성립한다고 할 수 있다.
표 9는 레벨 10에서 레벨 13까지의 학습 데이터에 본 논문에서 제안한 ARM+MSMM 방식을 적용하여 도출한 KC 선후관계 분석 결과를 요약한 것이다. 본 연구에서는 ARM 기법을 적용하여 얻은 결과 중 lift(상승도)가 큰 값으로 타겟 KC 관계의 수와 동일한 수의 관계를 선택하였다. 결국 표 9에 나타난 바와 같이 ARM 방식을 적용한 결과 데이터의 크기(②)가 타겟 KC 관계의 개수(①)와 동일하다.

KC prerequisite relation and accuracy rate after appying ARM+MSMM to the learning data from level 10 to level 13
표 9에서 알 수 있듯이 ARM only 방식과 ARM+MSMM 방식을 적용하여 도출한 목록과 타겟 KC 목록의 재현율(recall)은 비슷하게 나타난다. 그러나 각 방식에서 획득한 목록 중 타겟 KC 목록에 속한 항목의 비중을 나타내는 일치도(precision)는 ARM+MSMM 방식에서 개선된 것을 확인할 수 있다. 즉, ARM 방식만 적용했을 때보다 MSMM을 추가로 활용하여 시차를 반영한 데이터의 상태 변화를 고려함으로써 원래 정확도(precision)보다 2배 이상의 성과를 얻을 수 있었다.
V. 결 론
본 연구에서는 학습자 맞춤형 학습 경로(learning path)를 제시할 때 활용하는 지식 그래프(Knowledge Graph)의 정확도를 향상하기 위해 ARM과 MSMM 방식을 적용하여 지식 요소(KC) 간 선후 관계를 도출하는 RCA 분석 프로세스를 제안하고 초중등 레벨의 수학 문항 평가 데이터에 적용하여 그 결과를 분석하였다.
본 연구에서 제안한 ARM+MSMM을 활용한 RCA 분석 프로세스는 다음과 같다. 우선 1회차 문항 평가의 결과 데이터에 ARM 방식을 적용하여 유의미한 KC 관계를 도출한 후 신뢰도(0.4)와 지지도(0.001)의 하한을 만족하는 사건 중 KC A와 KC B의 정오답에 대한 조건부 확률을 기반으로 KC 간 선후관계를 결정하였다. 다음으로 앞서 ARM 분석을 통해 획득한 선후관계를 모집단으로 하여 1회차 테스트를 실시한 동일 학생 집단의 2회차 테스트 평가 결과에 대해 MSMM을 수행하여 최종의 KC간 선후관계를 정제한다. 이를 타켓 KC 선후관계 목록과 비교한 결과 ARM 분석으로만 확보한 KC 선후관계 목록의 일치도에 비해 ARM+MSMM 분석을 통해 확보한 KC 선후 관계 목록의 일치도가 모든 레벨에서 상승한 것을 확인하였다.
본 연구에서는 동일 집단의 학생에 대하여 크게 차이나지 않는 시차 내에 측정한 데이터를 사용함으로써 학생의 성적 변화가 선후관계에 영향을 미치지 않도록 조절하였으며, KC의 값을 이진(binary) 방식으로 표현했을 때 ARM 방식이 제공하는 척도 값 이상일 경우만 조건부 확률을 내준다는 특징을 보완하기 위해 MSMM 방식을 추가하여 KC간 선후관계의 추출을 더욱 용이하게 하였다.
결과를 활용하는 측면에서는 다음과 같은 두 가지 장점이 존재한다. 첫째, 학습자의 실제 학습 데이터로부터 전문가들이 일반적으로 알지 못했던 관계를 찾아내어 효과적인 학습을 유도할 수 있다. 전문가들은 그들의 경험과 사회적인 상식에 의존해 획득한 학습의 순서를 주장할 수 있다. 하지만, 학생이 실제로 학습을 통해 나타내는 데이터로부터 전문가가 예측해 내지 못하는 개념 간 선후관계를 얻을 수 있다.
둘째, 학습 데이터에 기반하여 ARM과 MSMM 방식이 산출하는 통계량으로부터 KC 관계의 강도를 객관적으로 도출할 수 있다. 즉 ARM에서는 관계의 신뢰도, 지지도, 상승도를 얻을 수 있고, MSMM으로부터 각 KC 개념의 습득 여부를 고려한 KC 선후관계에 대한 예측 확률을 얻을 수 있다.
그러나 이번 연구에서는 학습 데이터에서 나타날 수 있는 측정상의 오류를 고려하지 않은 채 조건부 확률의 개념을 적용하였다. 따라서 학생이 시험을 볼 때 나타날 수 있는 추측, 실수 등의 오차를 고려하여 KC간 선후관계를 결정하도록 학습 분석 모델을 강화하는 연구가 보완되어야 할 것이다.
Acknowledgments
본 연구는 2021년도 ㈜대교 사의 콘텐츠 개발실의 지원에 의해 이루어진 연구로서, 관계부서에 감사드립니다.
References
- Bae Ye-Seon, “Study on MOOC status and improvement plan”, Review of Korean Society for Internet Information, Vol. 17, No. 2, pp. 27-33, 2016. https://www.koreascience.or.kr/article/JAKO201609040218772.page
- D. S. Kang, J. K. Kim, and H. I. Chong, “The Structural relationship among affective characteristics, Learning presence, Learning flow, Learning satisfaction in Distance Education”, The Journal of Educational Information & Media, Vol. 17, No. 1, pp. 133-152, March, 2011. https://www.kci.go.kr/kciportal/ci/sereArticleSearch/ciSereArtiView.kci?sereArticleSearchBean.artiId=ART001541877
-
D. H. Yang, “Educational Problems with MOOC, Suggestions, and Convergence of MOOC and Universities” Journal of the Korea Convergence Society, Vol. 7, No. 3, pp. 121-129, 2016.
[https://doi.org/10.15207/JKCS.2016.7.3.121]

-
Myoung-Hoon, Seo, et al. "An Empirical Study on the Critical Factors Affecting Use Intension of Massive Open Online Courses (MOOC)." Journal of Digital Contents Society(J. DCS), Vol. 21, No. 2, pp. 293-300, Feb, 2020.
[https://doi.org/10.9728/dcs.2020.21.2.293]

-
Seyoung Kim, Eugene Lim, Bokyung Kim, Yekyung Lee, “An Analysis of Learner’s Experience in Distance Education at A University in the COVID-19 situation.” Journal of Korean Association for Education Information and Media, Vol. 27, No. 1, pp. 161-189, 2021.
[https://doi.org/10.15833/KAFEIAM.27.1.161]

-
Lee, J., Sung, E., Lee, J., Lim, K., & Han, S, “Challenges and tasks facing online classes during the COVID-19 pandemic.” Journal of Educational Technology, Vol. 36, No. 3, pp. 671-692, 2020.
[https://doi.org/10.17232/KSET.36.3.671]

-
Zhang, M., Zhu, J., Wang, Z., & Chen, Y, “Providing personalized learning guidance in MOOCs by multi-source data analysis.” World Wide Web, Vol. 22, No. 3, pp. 1189-1219, 2019.
[https://doi.org/10.1007/s11280-018-0559-0]

-
Shemshack, A., & Spector, J. M, “A systematic literature review of personalized learning terms.” Smart Learning Environments, Vol. 7. No. 33, pp. 1-20, 2020.
[https://doi.org/10.1186/s40561-020-00140-9]

-
Lee, D., Huh, Y., Lin, C. & Reigeluth, C. M, “Technology functions for personalized learning in learner-centered schools.” Educational Technology Research and Development, Vol. 66, pp. 1269-1302, 2018.
[https://doi.org/10.1007/s11423-018-9615-9]

- Brown et al. 2020 EDUCAUSE Horizon Report Teaching and Learning Edition, EDUCAUSE, pp. 14-16, 2020. Available: https://library.educause.edu/-/media/files/library/2020/3/2020_horizon_report_pdf.pdf?la=en&hash=08A92C17998E8113BCB15DCA7BA1F467F303BA80
-
Corbett, Albert T., and John R. Anderson. “Knowledge Tracking : Modeling the Acquisition of Procedural Knowledge” User modeling and user-adapted interaction, Vol. 4, No. 4, pp. 253-278, 1994. http://act-r.psy.cmu.edu/wordpress/wp-content/uploads/2012/12/893CorbettAnderson1995.pdf
[https://doi.org/10.1007/BF01099821]

-
Pan, L., Li, C., Li, J., & Tang, J., “Prerequisite relation learning for concepts in moocs.” In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, Vol. 1: Long Papers, pp. 1447-1456, July, 2017.
[https://doi.org/10.18653/v1/P17-1133]

-
Lu, W., Zhou, Y., Yu, J., & Jia, C., “Concept extraction and prerequisite relation learning from educational data.” In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33, No. 1, pp. 9678-9685, July, 2019.
[https://doi.org/10.1609/aaai.v33i01.33019678]

-
Corbett, A. T. and Anderson, J. R., “Knowledge tracing: Modeling the acquisition of procedural knowledge.” User Modeling and User-Adapted Interaction, Vol. 4, No. 4, pp. 253-278, 1995.
[https://doi.org/10.1007/BF01099821]

- Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L. J., & Sohl-Dickstein, J., “Deep knowledge tracing.” Advances in neural information processing systems, Vol. 28, Jan, 2015. https://proceedings.neurips.cc/paper/2015/file/bac9162b47c56fc8a4d2a519803d51b3-Paper.pdf
-
P. Chen, Y. Lu, V. W. Zheng and Y. Pian, "Prerequisite-Driven Deep Knowledge Tracing" 2018 IEEE International Conference on Data Mining (ICDM), pp. 39-48, 2018.
[https://doi.org/10.1109/ICDM.2018.00019]

-
d Baker, Ryan SJ, Albert T. Corbett, and Vincent Aleven, “More accurate student modeling through contextual estimation of slip and guess probabilities in bayesian knowledge tracing.” International conference on intelligent tutoring systems. Springer, pp. 406–415, 2008.
[https://doi.org/10.1007/978-3-540-69132-7_44]

-
Pardos, Zachary A., and Neil T. Heffernan, “KT-IDEM: Introducing item difficulty to the knowledge tracing model.“ International Conference on user modeling, adaptation, and personalization. Springer, Berlin, Heidelberg, pp. 243–254, 2011.
[https://doi.org/10.1007/978-3-642-22362-4_21]

-
Chen, Penghe & Lu, Yu & Zheng, Vincent & Chen, Xiyang & Yang, Boda,. “KnowEdu: A System to Construct Knowledge Graph for Education.” Ieee Access, Vol. 6, 2018.
[https://doi.org/10.1109/ACCESS.2018.2839607]

- How to Use the Fishbone Tool for Root Cause Analysis [Internet]. Available: https://www.cms.gov/medicare/provider-enrollment-and-certification/qapi/downloads/fishbonerevised.pdf
- Solé-Simó, Marc & Muntés-Mulero, Victor & Rana, Annie & Estrada, Giovani, “Survey on Models and Techniques for Root-Cause Analysis” arXiv preprint arXiv:1701.08546, 2017.
- Knowledge Map [Internet]. Avaliable: https://khanacademy.fandom.com/wiki/Knowledge_Map
-
Shi, Daqian, et al. “A learning path recommendation model based on a multidimensional knowledge graph framework for e-learning.” Knowledge-Based Systems, Vol. 195, No. 105618, 2020.
[https://doi.org/10.1016/j.knosys.2020.105618]

-
Kalbfleisch, J. D., and J. F. Lawless. “The Analysis of Panel Data Under a Markov Assumption.” Journal of the American Statistical Association, Vol. 80, No. 392, pp. 863-871, 1985.
[https://doi.org/10.1080/01621459.1985.10478195]

-
Hill, M., Lambert, P.C. & Crowther, M.J. “Relaxing the assumption of constant transition rates in a multi-state model in hospital epidemiology.” BMC medical research methodology, Vol. 21, No. 1, pp. 1-10, 2021.
[https://doi.org/10.1186/s12874-020-01192-8]

저자소개

1997년 : 고려대학교 대학원 (이학석사)
2019년 : 호서대학교 대학원 (통계학 박사)
1996년~2012년: 한국 IBM 소프트웨어 연구소 부장
2012년~2014년: 환경부 IT 전문위원
2015년~2017년: 데이터 솔루션 수석 컨설턴트
2020년~현 재: 라이브데이터(주) 수석 연구원
※관심분야 : 데이터 분석, 데이터 사이언스, 에듀테크

1994년 : 중앙대학교 컴퓨터공학과 (공학사)
1996년 : KAIST 전산학과 (공학석사)
1996년~2000년: ㈜ LG전자 LG종합기술원 연구원
2000년~2010년: ㈜ 아이에이 수석연구원
2011년~2015년: ㈜ 삼성전자 소프트웨어센터 부장
2016년~현 재: 중앙대학교 다빈치교양대학 조교수
2018년~현 재: 고려대학고 컴퓨터학과 박사과정
2021년 ~현 재: 라이브데이터(주) 연구소장
※관심분야:SW교육, 인공지능 리터러시, 기계학습, 에듀테크