국산 경량 블록 암호 PIPO, HIGHT, CHAM 고속 구현 연구

2-1 CTR 모드 최적화 구현 기법

CTR 모드는 블록 암호 운영 모드 중 하나로, 다수의 블록을 암호화하기 위해 사용된다. CTR 모드는 1씩 증가하는 카운터를 암호화한 후 평문 블록과 XOR 하여 암호문을 생성한다. 블록을 미리 암호화하는 사전 계산이 가능하다는 장점으로 가장 널리 사용되는 운영 모드 중 하나이다. CTR 모드는 현재 Open Mobile Applance (OMA) 및 Digital Right Management (DRM) 등과 같이 다양한 서비스에 사용된다. 또한, GCM, CCM과 같이 암호화와 동시에 연관 데이터에 대한 인증값을 생성하는 Authentication Encryption Assodicated Data (AEAD) 스킴을 만들기 위해 CTR 모드가 사용되기도 한다[14][15].

CTR 모드 최적화 구현 기법은 카운터 값이 1씩 증가하는 CTR 모드의 특징을 이용한다. 해당 기법은 암호화가 수행되는 입력 평문 중 카운터 값의 증가로 인한 영향을 거의 받지 않는 비트들에 대한 사전 계산 결과를 캐싱하여 최적화한다. CTR 모드 최적화 구현 기법은 8bit, 16bit, 32bit 등 모든 환경에 적용 가능하며, 테이블 기반의 구현 및 비트 슬라이스 구현 등과 같이 다른 구현물에도 적용 가능하다는 장점이 있다.

그림 1은 AES 알고리즘에 CTR 모드 최적화 구현 기법을 적용한 것을 보여준다[16]. 그림 1의 흰색으로 칠해진 영역은 CTR 모드의 입력 평문 중 카운터 값이 증가하는 것에 따라 변경되지 않는 바이트를 의미하며, 매 실행시 동일한 값을 가진다. 붉은색으로 칠해진 영역은 CTR 모드의 입력 평문 중 카운터 값으로 변경되는 비트들의 영역을 표시한 것으로, 매 실행시 다른 값을 가진다. CTR 모드 최적화 구현 기법은 흰색으로 칠해진 영역만을 입력으로 하는 연산의 결과를 캐싱하고, 흰색 영역과 붉은색 영역이 연관되어 입력되는 연산을 축소시켜 최적화를 수행한다.

Fig. 1.

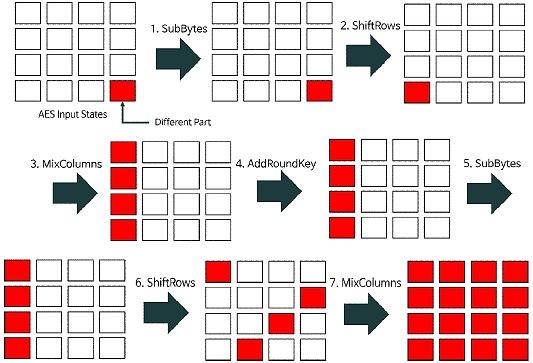
The bytes area of input plaintexts affected by increase of the counter value and the bytes area not affected by increase of counter value in AES-CTR process

그림 1은 AES 알고리즘의 동작 과정에 따라 CTR 모드 입력 평문이 모두 카운터 값에 영향을 받아 매 실행마다 값이 다른 붉은색 영역이 되는 과정을 보여준다. AES 동작 과정에 따라 흰색 영역은 다음과 같이 붉은색 영역의 영향을 받는다. 먼저, AES 알고리즘의 SubBytes 과정은 각 상태 바이트들을 치환하는 과정으로 입력이 같다면 같은 출력을 생성하여 흰색 영역이 그대로 유지된다. 이후, ShiftRows 과정은 상태 바이트의 위치를 변경하는 과정으로, 흰색 영역과 붉은색 영역의 위치만 변경된다. 반면에 MixColumn 과정의 경우에는 상태 배열의 한 열이 연산 과정에 의해 치환되는 과정이다. 따라서 흰색 영역만으로 입력이 구성된 영역은 MixColumn 연산 이후 모두 흰색으로 출력되지만 붉은색 영역이 하나라도 섞인다면 모두 붉은색으로 출력된다. 마지막으로 AddRoundKey 연산은 모든 상태 바이트에 라운드 키를 XOR 하는 연산으로 흰색 영역과 붉은색 영역이 그대로 유지된다. 따라서 그림 1과같이 AES 알고리즘의 동작 과정에 따라 마지막 1바이트 붉은 영역이 SubBytes 과정을 통해 그대로 유지되고, ShiftRows 과정을 통해 위치가 변환되고, MixColumn 과정을 거쳐 총 4개의 흰색 영역으로 확산된다. 이후, AddRoundKey 과정과 SubBytes 과정을 통해 그대로 유지되고, ShiftRows 과정을 통해 4개의 붉은색 영역의 위치가 변경되며 마지막으로, MixColumns 과정을 통해 모든 상태의 바이트가 붉은색 영역이 된다.

[16]은 그림 1의 AES를 대상으로 CTR 모드 최적화 구현을 수행하여 2개의 AddRoundKey, 2개의 SubBytes, 2개의 ShiftRows, 그리고 1개의 MixColumn 연산 결과를 사전 계산하여 최적화를 수행하였으며, 기존 테이블 기반 구현보다 15-20% 속도 향상을 이뤘다.

CTR 모드 최적화 구현 기법은 2019년 CHES에서 처음 발표된 연구[16]를 시작으로 다양한 환경과 알고리즘을 대상으로 활발히 연구가 수행되었다. [17]은 자원이 제한된 8bit AVR 환경에서 적용 가능한 CTR 모드 최적화 기법을 제안하였으며, AES 알고리즘의 성능을 22% 개선하였다.

이후 2020년에는 ARIA 알고리즘을 대상으로 CTR 모드 최적화 구현 연구가 수행되었으며, 2개의 AddRoundKey, 1개의 SubstituteLayer, 그리고 1개의 DiffusionLayer 라운드 연산을 미리 계산하여 69% 성능 향상을 이루었다[18].

또한 2020년에는 8bit AVR 환경에서 HIGHT, LEA 알고리즘과 CTR_DRBG (Deterministic Random Bit Generator) 알고리즘을 대상으로 CTR 모드 최적화 구현 연구가 수행되었다[19]. LEA와 HIGHT 알고리즘을 대상으로 CTR 모드 최적화 수행 결과 6.3%, 3.8% 성능 향상이 이뤄졌으며, CTR_DRBG 구현은 블록 암호가 LEA, HIGHT를 사용할 때, 각각 37.2%, 8.7% 성능 향상이 이뤄졌다.

2021년에는 ARX 기반 암호 알고리즘 LEA, HIGHT, CHAM 알고리즘을 대상으로 ARMv8 환경에서 CTR 모드 최적화 구현 연구가 수행되었다[20]. CTR 모드 최적화 구현을 통해 LEA를 대상으로 4라운드, HIGHT를 대상으로는 5라운드, CHAM을 대상으로 7라운드를 최적화 구현하였으며, 각각 8.76%, 8.67%, 15.87% 성능 향상이 이뤄졌다.

그러나 CTR 모드 최적화 구현에 관한 기존 연구들은 특정 암호 알고리즘을 대상으로 적용하는 연구만 이뤄졌으며, 모든 알고리즘에 적용 가능한 방법론에 관한 연구가 수행되지 않았다. 이에, 본 논문은 CTR 모드 최적화 구현 기법을 블록 암호에 적용하는 일반적인 방법론을 소개하고, CTR 모드 최적화 구현 연구가 이뤄지지 않은 PIPO 알고리즘에 대해 CTR 모드 최적화 구현 기법을 적용한 결과를 소개한다.

CTR 모드 최적화 구현 기법을 임의의 블록 암호에 적용하기 위해서는 다음의 내용을 고려해야 한다.

• - 암호 알고리즘마다 동작 과정이 다르므로 암호 알고리즘의 동작상의 특징에 맞게 최적화를 수행해야함
• - 카운터 값이 1씩 증가함에 따라 자주 변경되는 하위 비트와 거의 값이 변경되지 않은 상위 비트를 입력으로 하는 암호 알고리즘의 동작 과정을 분석해야 함
• - 알고리즘의 라운드 함수에 따라 최적화 결과가 상이함

2-2 비트 슬라이스 구현 기법

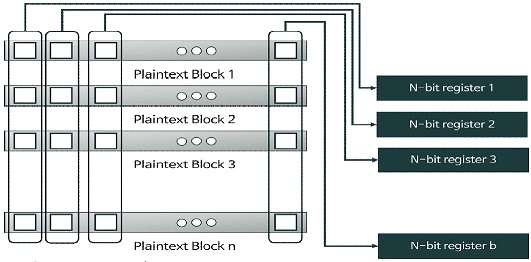
비트 슬라이스 구현 기법은 DES의 성능을 증가시키기 위해 Biham이 최초로 제안한 구현 기법으로[21], 입력 평문을 비트 단위로 쪼개서 마치 하드웨어와 같이 암호 알고리즘을 동작시키는 구현 기법이다. 그림 2는 비트 슬라이스 데이터 구조로 n개의 평문 블록을 비트 순서대로 정렬하는 packing 과정을 보여준다. 비트 슬라이스 구현 기법은 packing 과정의 대상이 되는 블록 수 만큼 한 번에 여러 개의 평문이 동시에 처리되게한다.

Fig. 2.

Data structure of bitslice

비트 슬라이스 구현은 다음과 같은 장단점이 존재한다. 비트 단위의 masking 연산과 rotation 연산을 효율적으로 수행할 수 있다는 장점이 존재한다. 또한 키와 입력값에 상관없이 동일한 시간이 소요되어 timing attack에 저항성이 있다는 장점이 있다. 병렬로 처리하는 평문 블록의 숫자로 워드 크기가 결정되므로 대상 암호 알고리즘의 워드 크기와 다르게 암호 알고리즘을 동작시킬 수 있다는 장점이 있다. 그러나 비트 슬라이스 구현 기법은 암호 알고리즘의 동작 과정이 비트 단위의 연산으로 구성되어야 적용할 수 있다는 단점이 있다. 또한, 암호 알고리즘 동작 전/후로 수행되는 packing/unpacking 과정의 오버헤드가 존재한다.

비트 슬라이스 구현 기법은 Biham이 최초로 제안한 이후[21], 2006년에 AES 알고리즘을 대상으로 비트 슬라이스 구현에 관한 연구가 수행되었다[22]. 이후, 2016년에는 PRINCE, LED, RECTANGLE 블록 암호를 대상으로 AVR 8bit 환경에서 비트 슬라이스 구현에 관한 연구가 수행되었으며[23], 2018년에는 LED 알고리즘을 대상으로 64bit 환경인 ARM Cortex-A53에서 비트 슬라이스 구현 연구가 수행되었다[24]. 또한, 최근에는 암호 알고리즘을 설계하면서 비트 슬라이스 구현을 고려하여 암호 알고리즘의 S-box를 비트 단위의 논리 연산자로 구성하기도 한다. PIPO, RoundRunnR[25] 등의 알고리즘이 비트 슬라이스로 구현될 수 있는 S-box를 가진다.

그러나 국내 경량 블록 암호 알고리즘을 대상으로 한 비트 슬라이스 구현 연구는 매우 제한적으로 이뤄졌다. 2012년에 HIGHT 알고리즘을 대상으로 비트 슬라이스 구현 연구가 수행되었으나[26], 32/64bit PC 운영체제에서만 실험을 진행했다는 한계점이 존재한다.

이에, 본 논문은 ARX 기반 암호 알고리즘을 대상으로 비트 슬라이스 기법을 적용하는 방법론을 소개하고, ARX 기반 국내 블록 암호 HIGHT, CHAM을 대상으로 비트 슬라이스 기법을 적용한 결과를 소개한다. 또한, 비트 슬라이스 구현한 알고리즘에 대한 성능을 각각 32-bit, ARM Cortex M4, x86 PC 환경에서 측정하여 비교한다.

비트 슬라이스 구현 기법을 임의의 블록 암호에 적용하기 위해서는 다음의 내용을 고려해야 한다.

• - 암호 알고리즘의 동작 과정을 AND, OR, NOT 등과 같이 간단한 논리 게이트의 조합으로 변경 가능해야 함
• - 레지스터의 수가 적으면 일부 데이터를 메모리에 저장하는 오버헤드가 발생함
• - packing, unpacking 과정의 오버헤드를 고려하여 비트슬라이스 구현 여부를 결정해야 함

2-3 대상 암호 알고리즘

본 논문에서는 PIPO, HIGHT, CHAM 알고리즘을 대상으로 최적화 구현을 수행한다. 본 논문에서 다루는 최적화 구현 기법은 암호 알고리즘의 라운드 동작 과정을 대상으로 최적화를 수행하므로 본 절에서는 각 알고리즘의 라운드 동작 과정만을 소개한다.

1) PIPO 알고리즘

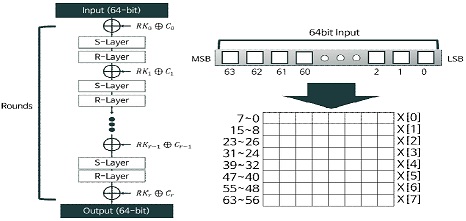
PIPO는 64-bit 크기의 평문, 128/256-bit 크기의 키를 사용하는 SPN 구조 암호 알고리즘이다. PIPO는 128-bit 키 사용 시 13라운드, 256-bit 키 사용 시 17라운드로 구성되며, 각 라운드는 AddRoundKey, S-Layer, P-Layer로 구성된다. PIPO는 8×8bit 배열의 상태(state)로 동작하며, 전체적인 동작 과정은 그림 3과 같다.

Fig. 3.

The process and state of PIPO

라운드 과정 중 AddRoundKey 과정은 라운드 키 RK_i와 라운드 상수C_i를 입력 평문과 XOR 연산하는 과정이다. S-Layer는 8×8bit 상태 배열의 열 단위로 S-box 테이블을 참조하는 과정이다. 테이블 참조 구현 시 S-box 테이블 참조를 위해 가로 행과 세로 열의 비트를 변경하는 연산이 테이블 참조 전후로 수행되어야 한다. R-Layer는 8×8bit 상태 배열의 행 단위로 Rotation 연산을 수행하는 과정이다. 첫 번째 행은 Rotation 연산을 수행하지 않으며, 두 번째 행부터 7, 4, 3, 6, 5, 1, 2-bit Rotation 연산을 수행한다.

2) HIGHT 알고리즘

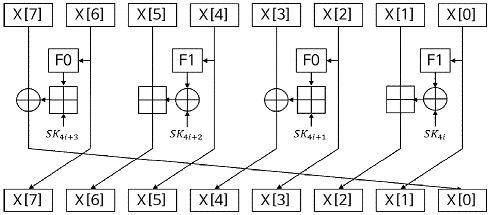
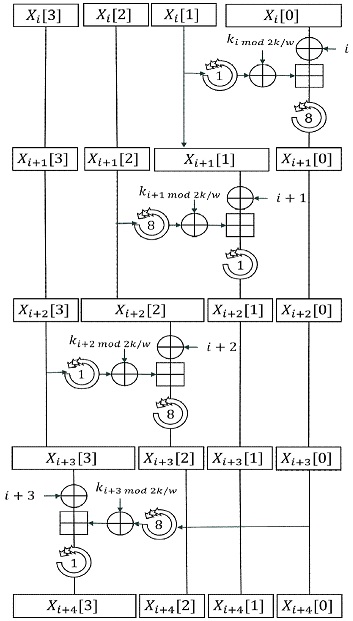
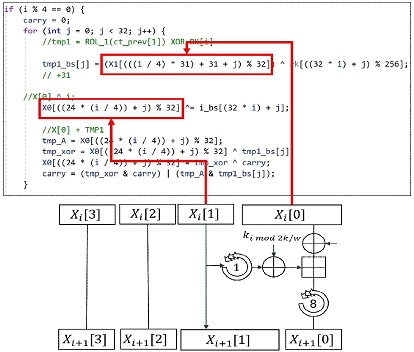
HIGHT 알고리즘은 ARX 기반 경량 블록 암호로 64-bit 길이의 평문, 128-bit 키 길이를 가진다. 저전력 프로세서에서 효율적으로 동작할 수 있게 8bit 단위의 Addition, Rotation, Xor 연산으로 라운드 동작 과정이 구성되어 있으며, 32라운드로 동작한다. HIGHT 알고리즘의 라운드 동작 과정은 그림 4와 같다.

Fig. 4.

The process of HIGHT cipher

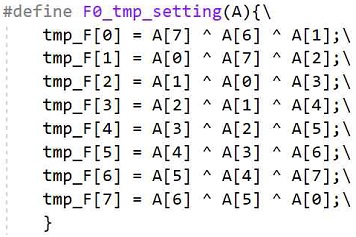
그림 4의 F0 연산은 $$ F_0\left(X\right)=X^{⋘1}\otimes X^{⋘2}\otimes X^{⋘7}$$으로 정의되며, F1 연산은 $$ F_1\left(X\right)=X^{⋘3}\otimes X^{⋘4}\otimes X^{⋘6}$$으로 정의된다.

3) CHAM 알고리즘

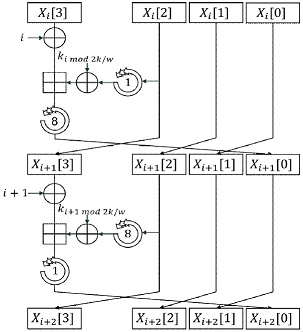
CHAM 알고리즘은 ARX 기반 경량 블록 암호로 평문과 키 길이가 다른 CHAM-64/128, CHAM-128/128, CHAM-128/256 세 가지 인스턴스가 존재한다. 각 인스턴스에 대한 평문의 비트 수, 라운드, 워드 크기는 표 1와 같다.

Table 1.

3 Instance of CHAM cipher

CHAM 알고리즘의 인스턴스 중 CHAM-64/128은 워드 크기로 인해 저전력 프로세서에서 효율적으로 동작하지만, 범용 환경에서는 상대적으로 비효율적으로 동작한다. 본 연구는 범용 환경에서 CHAM-64/128 알고리즘을 32bit 및 범용 환경에서 효율적으로 동작시키기 위해 비트 슬라이스 구현을 수행하였다. CHAM 알고리즘의 라운드 함수는 그림 5와 같다.

Fig. 5.

The process of CHAM cipher

3-1 CTR 모드 최적화 구현 적용 방법과 PIPO 알고리즘에의 적용

CTR 모드 최적화 구현 기법은 1씩 증가하는 카운터 값에 따라 자주 변하는 하위 몇 비트를 제외한 나머지 평문의 비트들이 고정되어 동일하게 입력된다는 특징을 이용하는 최적화 구현 기법이다. 본 논문에서는 CTR 모드로 동작하는 암호 알고리즘의 입력 평문 블록 중 카운터 값의 증가로 변경되지 않는 영역을 고정 영역이라 정의하고, 평문 블록 중 카운터 값의 증가로 변경되는 비트의 영역을 카운터 영역이라 정의한다. 카운터 영역은 입력 평문으로부터 LSB n 비트로 구성되며, 고정 영역은 나머지 비트로 구성된다. CTR 모드 최적화 구현 기법은 고정 영역에 대한 연산 결과를 사전 계산하여 이후의 여러 입력 블록에 대한 암호 알고리즘의 동작 과정을 생략, 축소하여 최적화한다.

CTR 모드 최적화 구현 기법이 적용되는 임의의 알고리즘은 Confusion과 Diffusion 원리를 기반으로 설계되고, 워드 단위로 동작한다고 가정한다. 본 논문에서 제안하는 임의의 알고리즘을 대상으로 CTR 모드 최적화 구현 기법을 적용하는 방안은 다음과 같다.

먼저, 입력 평문 블록의 카운터 영역과 고정 영역을 설정한다. 카운터 영역의 크기는 임의로 지정할 수 있다. 그 이유는 카운터 영역의 길이만큼 고정 영역에 대한 연산을 생략하는 캐시 테이블을 구성하여 사용할 수 있으며, 카운터 값이 고정 영역의 비트를 변경할 때 구성한 캐시 테이블을 변경된 고정 영역에 맞게 새로 갱신할 수 있기 때문이다. 그러나, 카운터 영역 및 고정 영역의 크기는 암호 알고리즘의 동작상의 특징고 실행 환경을 고려하여 설정해야 한다. 카운터 영역의 크기가 작다면 고정 영역의 범위가 증가해, 생략/축소할 수 있는 연산의 범위가 커지지만, 사전 계산 테이블을 자주 갱신해야 하는 문제점이 있다. 또한, 카운터 영역의 크기가 너무 크다면 사전 계산 테이블의 크기가 너무 커질 수 있고 고정 영역이 줄어들어 생략/축소할 수 있는 연산의 범위가 줄어들 수 있다. 카운터 영역의 크기는 주로 암호 알고리즘의 워드 사이즈의 배수로 설정할 수 있다.

두 번째 과정으로, 고정 영역의 비트/워드만으로 암호 알고리즘의 Confusion이 수행되는 영역을 탐색하여 해당 연산을 생략한다. 카운터 영역을 대상으로 Confusion이 수행된다면 해당 영역은 매 실행마다 다른 입력값에 따라 다른 출력을 생성한다. 고정 영역만을 대상으로 Confusion이 수행된다면, 해당 영역은 매 실행마다 동일한 출력을 생성한다. 따라서, 고정 영역만을 입력으로 하는 Confusion 과정의 출력값을 사전 테이블에 저장하여 생략할 수 있다.

세 번째 과정은 설정한 카운터 영역의 비트/워드와 고정 영역의 비트/워드과 연관되어 Confusion 과정이 이뤄지는 범위를 탐색하여 연산 생략을 고려한다. 입력 평문 중 고정 영역의 비트/워드가 카운터 영역의 비트/워드와 연관되어 Confusion이 수행될 시, 카운터 영역의 비트 범위가 한정되므로 Confusion 출력의 범위가 제한된다. 따라서, 카운터 영역에 올 수 있는 값에 대한 Confusion 출력을 캐시 테이블에 저장하여 연산을 생략할 수 있다. 그러나 캐시 테이블의 크기를 고려하여 암호 알고리즘의 특성과 운영 환경에 맞게 해당 연산의 생략 여부를 결정해야 한다. 이후 Confusion 출력을 모두 카운터 영역으로 취급한다.

마지막 과정은 암호 알고리즘의 Diffusion 과정을 고려하여 캐시 테이블을 설정하는 과정이다. Diffusion 과정은 카운터 영역의 입력값과 무관하게 동일한 과정이 수행된다. 따라서, 캐시 테이블을 이용하여 해당 Diffusion 연산이 수행된 이후의 위치로 비트를 배치하여 Diffusion 연산을 생략할 수 있다. 그러나, 암호 알고리즘의 Diffusion 과정이 비트 단위로 수행되는 등의 과정으로 인해 캐시 테이블에 저장된 값을 블록에 배치하는 연산량보다 해당 암호 알고리즘 동작 과정 연산량이 더 적거나, 캐시 테이블이 너무 커지는 경우가 존재한다. 따라서 암호 알고리즘의 특성과 운영 환경에 따라 암호 알고리즘의 연산을 결정한다.

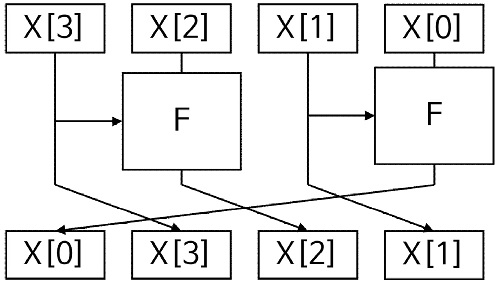
본 논문에서 제안하는 CTR 모드 최적화 구현 기법 적용 방법론은 Confusion과 Diffusion 원리를 기반으로 설계되고 워드 단위로 동작하는 임의의 암호 알고리즘에 적용할 수 있다. 본 논문은 제안하는 방법론을 예를 들어 설명하기 위해 그림 6과 같이 동작하는 임의의 암호 Cipher_A를 설정하였다.

Fig. 6.

The encryption process of Cipher_A

그림 7은 제안하는 CTR 모드 적용 방법론에 따라 Cipher_A를 최적화 구현하는 과정을 보여준다. 첫 번째 과정으로 카운터 영역을 1워드 크기로 설정하였다. 이후 두 번째 과정으로 고정 영역만으로 입력이 구성된 Confusion 과정을 찾는다. X[2]와 X[3]을 입력으로 하는 첫 번째 라운드 F함수와, 2라운드의 X[1]과 X[2]를 입력으로 하는 F함수가 고정 영역만을 입력으로 한다. 해당 영역에 대한 연산 결과를 캐시 테이블에 저장하는 것으로 해당 연산을 생략할 수 있다. 세 번째 과정으로 고정 영역과 카운터 영역이 연관되어 Confusion 과정이 수행되는 과정을 탐색한다. 1라운드의 X[0]와 X[1]을 입력으로 하는 F 연산이 이에 해당되며, 해당 연산 결과를 캐시 테이블에 저장해서 연산 생략을 고려할 수 있다. Cipher_A의 1워드 크기가 8-bit 라고 했을 때, 해당 연산을 생략하기 위해서는 2⁸×8 bits 크기의 캐시 테이블이 필요하다. 이후의 2라운드 X[0], X[3]을 입력으로 하는 F연산 또한 생략을 고려할 수 있으며, 해당 연산 결과를 캐시 테이블에 저장하기 위해서는 추가적으로 2⁸×8 bits 크기가 더 필요하다. 고정 영역과 카운터 영역이 연관되어 Confusion 과정이 수행되는 과정에 대한 캐시 테이블 구성은 암호 알고리즘을 동작시키는 환경을 고려하여 결정한다. 마지막, 네 번째 과정으로는 Diffusion을 고려하여 캐시 테이블을 설계하는 과정이다. Cipher_A 알고리즘은 워드 단위의 Diffusion 연산만으로 구성되어 있으므로 캐시 테이블에 저장된 값을 바로 평문 블록에 대입할 수 있어 고려하지 않는다.

Fig. 7.

The application of CTR mode optimization Implementation on Cipher_A

1) PIPO 알고리즘 CTR 모드 최적화 구현 적용

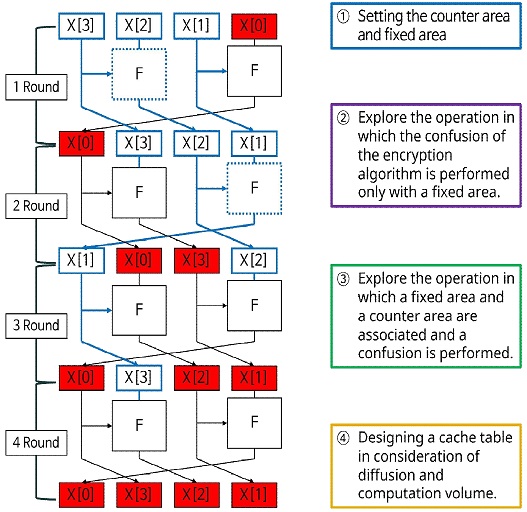
PIPO 알고리즘을 대상으로 CTR 모드 최적화 구현을 적용하기 위해서는 다음과 같은 과정이 수행되어야 한다. 첫쩨로, 카운터 영역과 고정 영역을 결정한다. 둘째로, 고정 영역만으로 암호 알고리즘의 Confusion이 수행되는 영역을 탐색한다. 셋째로, 고정 영역과 카운터 영역이 연관되어 Confusion이 수행되는 영역을 탐색한다. 마지막으로, Diffusion 과정에 대한 연산량을 고려하여 캐시 테이블을 설정한다. PIPO 알고리즘을 대상으로 CTR 모드 최적화 구현이 적용되는 과정은 그림 8과 같다.

Fig. 8.

The application of CTR mode optimization Implementation on PIPO

PIPO 알고리즘은 8×8bit 배열의 상태로 동작하며, 카운터 영역은 비트 단위로 고려한다. 본 논문에서는 PIPO가 8-bit 환경을 대상으로 설계된 경량 암호임을 고려하여 8-bit 길이의 카운터 영역을 설정하였으며 2⁸회당 1회 사전 계산 테이블을 계산하도록 하였다. 그림 8에서는 PIPO 알고리즘의 입력 평문 블록 중 카운터 영역을 색으로 표현하였으며, 고정 영역을 흰색으로 표현하였다. PIPO 알고리즘의 동작 과정에 따라 각 카운터 영역의 비트가 고정 영역의 비트에 영향을 주는 범위를 각 카운터 영역의 색으로 표현하였다.

먼저, PIPO 알고리즘의 AddRoundKey 과정은 입력의 모든 비트가 독립적으로 라운드 키의 비트와 XOR 연산을 수행하는 과정이다. 고정 영역에 대한 입력 평문과 라운드 키 입력이 동일하므로 고정 영역에 대해 연산 결과를 캐시 테이블에 저장하여 연산 과정을 생략할 수 있다.

이후의 과정인 S-Layer는 8×8bit 배열의 열 단위로 수행되는 연산으로, 테이블 참조 연산의 경우 행과 열의 비트를 재조합하는 transform 연산이 S-box 참조 연산 전후로 수행되어야 한다. S-box 테이블 참조의 입력값은 카운터 영역 1bit 그리고 고정 영역 7bit로 구성되어 있다. 따라서, S-box 출력 값은 1bit 카운터 영역에 의해 결정되며 S-box 출력에 대한 사전 계산 테이블을 통해 생략 가능하다. 이때 사전 계산 테이블의 크기는 8×2×8bits이다. 이후 S-box 출력을 모두 카운터 영역으로 취급한다. 이후 PIPO 알고리즘의 Confusion 연산은 모두 카운터 영역으로만 입력이 이뤄지기 때문에 고려하지 않는다.

S-box 이후 Diffusion 연산인 행과 열의 비트 순서가 변경되는 연산, 그리고 R-Layer 연산이 수행된다. 상태의 모든 비트가 카운터 영역이 되었으므로, Diffusion 연산 결과 비트를 모두 테이블에 저장해야 해당 연산을 생략할 수 있다. R-Layer의 연산 결과를 캐시 테이블에 저장한다면 캐시 테이블의 크기는 16,384(2⁸×64)bits가 된다. 캐시 테이블의 크기가 너무 큰 경우 자원이 제한된 환경에서 비효율적으로 동작할 수 있으므로, 연산의 축소/생략 없이 PIPO 알고리즘의 동작 과정을 그대로 수행하도록 한다.

따라서 PIPO 알고리즘을 대상으로 CTR 모드 최적화 구현 기법을 통해 1 라운드 연산을 최적화 할 수 있다. 최적화 구현에 사용되는 캐시 테이블은 카운터 영역 8bit에 대한 S-box 출력 결과로 구성된 128(8×2×8)bit 크기로 구성된다. 사전 계산 캐시 테이블을 사용해 PIPO 알고리즘 동작 중 AddRound Key 과정과 S-Layer의 Transform 과정을 1회 생략할 수 있으며, 사전 계산은 256(2⁸)회당 1회 수행된다.

3-2 ARX 기반 암호 알고리즘을 대상으로 한 비트 슬라이스 구현 방법과 HIGHT, CHAM 알고리즘에의 적용

ARX 기반 암호는 Addition, Rotation, XOR의 3가지 연산만 사용하여 암호화를 수행하는 암호를 의미한다. 알고리즘이 간단하여 구현하기가 쉽고 timing attack에 저항성이 있다는 장점이 있다.

ARX 기반 암호 알고리즘을 비트 슬라이스로 구현하기 위해서는 Addition, Rotation, XOR 연산을 각각 비트 단위의 논리 게이트의 조합으로 변환해야 한다. 본 논문은 다음과 같은 방법으로 ARX 기반 암호 알고리즘의 각 연산을 비트 단위로 처리되게 하여 비트 슬라이스로 구현 가능하게 하였다.

• 1. Addition 연산은 워드 단위로 동작하는 연산으로 받아올림(carry) 값 때문에 여러 비트가 연관되어 동작한다. 이를 비트 단위의 동작으로 변환하기 위해 carry 변수를 할당하고 Full Adder 논리 구조를 적용하였다. 워드 단위의 마지막 비트 자리부터 동작하며, 할당한 carry 변수를 포함한 세 비트에 대한 논리 연산자 조합으로 덧셈 결과 값과 carry 변숫값을 결정한다. 이 중 첫 번째 비트와 마지막 비트는 각각 이전 carry 값과 이후의 carry 값을 고려하지 않아도 되므로, n 비트 워드 단위의 덧셈 연산이라고 할 때, 비트 슬라이스로 변환한 총 논리 연산자의 숫자는 XOR 연산자 2n-1개 AND 연산자 2n-3개, OR 연산자 n-2개로 결정된다.
• 2. Rotation 연산은 워드 단위의 Rotation 연산과 비트 단위의 Rotation 연산으로 분류된다. 먼저 워드 단위의 Rotation 연산은 두 가지 방법으로 변환 가능하다. 첫 번째 방법은 워드 단위 Rotation 연산 전/후의 라운드 동작 과정을 매크로로 정의하여 라운드 동작마다 각 라운드에 맞는 입력 블록 비트 인덱스를 전달하여 워드 단위의 Rotation 연산을 한 효과를 주는 방법이다. 두 번째 방법은 워드 단위의 Rotation을 워드 숫자만큼 수행하여 동일한 워드가 동일한 라운드 함수 동작 과정을 수행할 때까지의 라운드를 재구성하는 방법이다. 비트 단위의 Rotation 연산은 워드 내의 비트의 순서를 변경하는 연산이다. 비트 슬라이스 구현은 입력 블록이 이미 비트 단위로 분리되어 암호 알고리즘의 라운드 과정을 진행하기 때문에, 라운드 함수 입력값의 인덱스를 계산하여 조절하는 것으로 rotation이 수행된 효과를 줄 수 있다. 만약 8bit 워드 w에서 1bit rotation 연산을 수행해야 한다면 다음 라운드 동작에서 w[k]대신 w[(k+7)%8]을 입력으로 전달하여 1bit rotation 연산을 수행한 효과를 줄 수 있다.
• 3. Xor 연산은 비트 단위의 연산이기 때문에 별도의 변환 과정을 수행하지 않는다.

1) HIGHT 비트 슬라이스 구현

본 논문은 HIGHT의 8bit 덧셈 연산을 그림 9와 같이, 그리고 F0 비트 단위 rotation 연산을 그림 10과같이 매크로로 정의하였다. 또한, HIGHT 라운드 함수를 그림 11과같이 정의하였으며, HIGHT 암호화 과정은 그림 12과같이 라운드 함수에 매개변수를 입력하는 것으로 비트 슬라이스 구현을 수행하였다. packing 과정과 unpacking 과정은 swapmove 기법[27]을 그림 13과같이 매크로로 구현하여 진행하였다.

Fig. 9.

The macro of addition operation on HIGHT cipher

Fig. 10.

The macro of F0 operation on HIGHT cipher

Fig. 11.

The macro of round on HIGHT cipher

Fig. 12.

Macro variable setting – HIGHT word uint roation operation

Fig. 13.

The macro of SWAPMOVE

2) CHAM 비트 슬라이스 구현

본 논문은 CHAM-64/128 알고리즘의 덧셈 연산을 그림 9와 같이 8bit 덧셈 연산으로 구현하였으며, 홀수, 짝수 라운드로 이뤄진 CHAM 라운드 동작 과정을 그림 14과 같이 4라운드 구조로 변경하여 워드 단위의 rotation 연산을 수행한 것과 같은 동작을 수행하게 했다. 또한, 비트 단위의 rotation 연산은 각 라운드가 끝나는 시점에서 이뤄지기 때문에, 그림 15와 같이 배열 인덱스를 설정하여 매 라운드 마다 rotation 연산이 수행된 것과 같이 동작하게 하였다. 마지막으로, packing 및 unpacking 과정은 HIGHT 비트 슬라이스 구현과 동일하게 그림 13의 swapmove 매크로를 사용하여 구현하였다.

Fig. 14.

The 4th round operation process of CHAM cipher

Fig. 15.

CHAM bit unit rotation operation

4-1 CTR 모드 최적화 구현 기법 적용 실험 결과

본 논문은 임의의 알고리즘을 대상으로 CTR 구현 기법을 적용하는 방법론을 제안하였으며 제안한 방법론을 이용하여 PIPO 알고리즘의 테이블 참조 구현을 최적화하였다. 본 논문에서는 PIPO 알고리즘의 공개 레퍼런스 코드의 1 라운드를 수정하여 최적화 구현을 수행하였으며, 나머지 라운드는 레퍼런스 코드와 동일한 코드를 사용하였다. PIPO 알고리즘은 8bit 환경을 대상으로 설계된 암호 알고리즘으로, 본 논문에서는 8bit AVR 과 x86 PC 환경에서 최적화 성능 측정을 수행하였다. 구현물의 이름과 설명은 표 2와 같다.

Table 2.

Description of CTR optimization implementation

8-bit 환경에서의 성능 측정 실험은 Atmel Studio를 이용하여 ATmega128 보드 시뮬레이터에서 성능을 측정하였으며 최적화 레벨은 0으로 하여 구현물의 성능을 비교했다. 성능 측정은 라운드 키를 생성하는 키 스케줄 과정을 제외하고 암호화가 진행되는 라운드 동작 함수만을 대상으로 했다. Atmel Studio의 디버깅 모드를 활용하여 성능을 측정하였다. 레퍼런스 코드와 최적화 구현물의 성능을 측정한 결과는 표 3과 같다. CTR 모드 최적화 구현을 위해 사전 계산을 수행하는 함수가 256회당 1회 수행됨을 고려하면, CTR 모드 최적화 구현물이 기존 레퍼런스 코드보다 3.96% 더 빠르게 암호화를 수행함을 확인할 수 있다.

Table 3.

Implementation performance in 8bit Atmega128 environment

x86 환경에서의 성능 측정 실험은 Windows 운영체제와 Intel Core i7-6700 CPU를 사용하는 환경에서 성능을 측정하였다. Visual Studio의 최적화 레벨 0으로 설정하여 c언어로 작성된 코드를 컴파일 하였으며, Windows 에서 CPU 클록을 받아오는 QueryPerformanceCounter 함수를 사용하여 최적화 구현물의 실행 시간을 측정했다[28]. x86 환경 PC에서 최적화 구현물의 성능을 측정한 결과는 표 4와 같다. x86 환경 PC에서 최적화 구현물이 레퍼런스 코드보다 5.48% 더 빠르게 암호화가 수행됨을 확인하였다.

Table 4.

CTR mode optimization implementation performance in x86 PC environment

4-2 비트 슬라이스 구현 기법 적용 실험 결과

본 논문은 ARX 기반 암호 알고리즘을 대상으로 비트 슬라이스 구현 방법을 제안하였으며 제안하는 방법론을 사용하여 HIGHT, CHAM을 비트 슬라이스 구현하였다. 비트 슬라이스 구현과 레퍼런스 코드 모두 동일한 연산을 수행하도록하였다. 실험은 32bit 환경과 x86환경 PC에서 수행되었다. 구현물의 이름과 설명은 표 5와 같다.

Table 5.

Description of bitslice implementation

32bit 환경은 ARM Cortex M4 프로세서를 사용하는 STM32F407G-DISC1 보드를 사용하여 성능을 측정하였다. STM32Cube IDE 1.7.0을 사용하여 c언어로 코드를 작성하였고, 최적화 레벨을 0으로 하여 성능을 측정하였다. 성능 측정은 DWT 레지스터를 사용하여 구현물의 클록 사이클을 측정하였다[29]. 32bit 환경에서의 레퍼런스 코드와 최적화 구현물의 성능을 측정한 결과는 표 6와 같다. 32bit 환경에서 16bit 환경을 대상으로 설계된 CHAM-64/128 암호 알고리즘과 8bit 환경을 대상으로 설계된 HIGHT 알고리즘은 각각 100%, 18.48%의 성능 향상이 이뤄졌다.

Table 6.

Bitslice implementation performance in 32bit STM32F407F-DISC environment

실험을 진행한 PC 환경은 CTR 모드 최적화 구현에 대한 성능을 측정한 x86 PC 환경과 동일한 환경을 사용하였다. x86 PC에서 최적화 구현물에 대한 성능을 측정한 결과는 표 7와 같다. CHAM-64/128의 경우에는 140% 성능 향상이 있었으며, HIGHT 알고리즘은 79.25% 성능 향상이 있었다.

Table 7.

Bitslice implementation performance in x86 PC environment