Inverse Haversine Method를 활용한 거리 기반 좌표 계산에 관한 연구

Ⅰ. 서 론

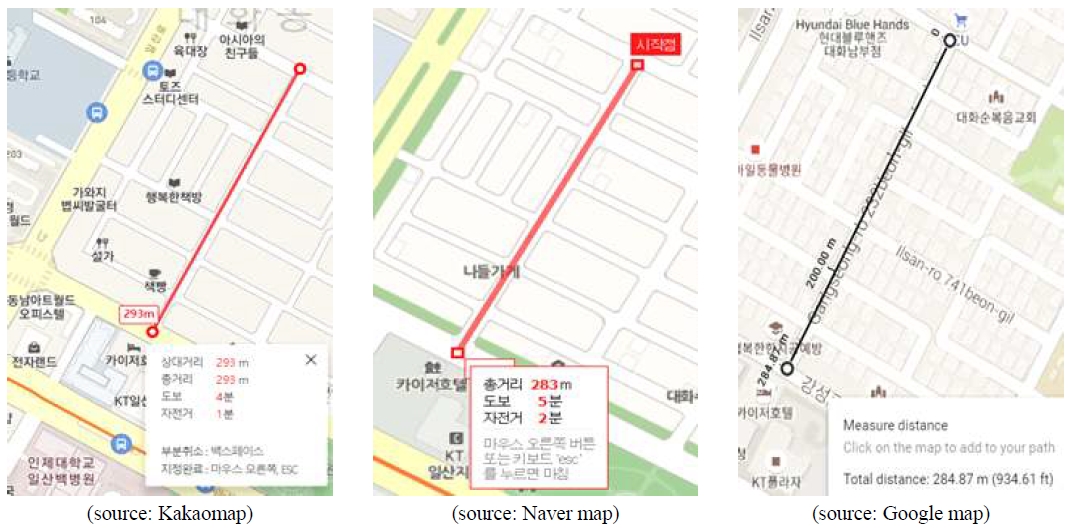
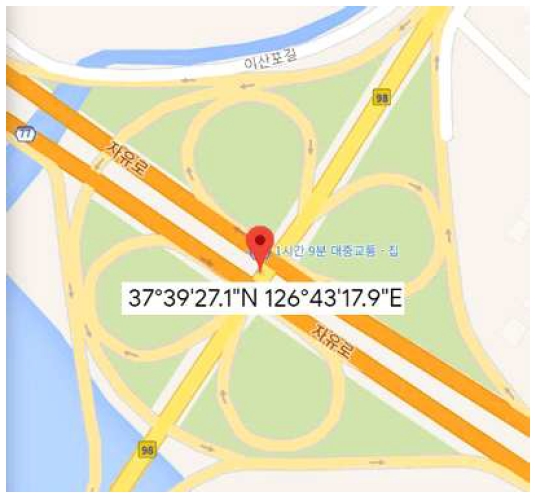
우리는 하루하루의 일상에서 이동이라는 행위를 하고, 그때마다 출발지로부터 목적지까지의 거리는 중요한 관심 정보가 된다. 이뿐만 아니라 내가 사는 집에서 가까운 지하철역까지의 거리, 백화점까지의 거리, 친구 집까지의 거리와 같이 관심 지점 간의 떨어진 정도는 우리에게 중요한 정보가 아닐 수 없다. 그래서 그림 1과 같이 대부분의 웹지도에서는 거리 측정 기능을 제공하고 있다.

Fig. 1.

Examples of the distance measurement of web-map services

만약 우리가 평평한 바둑판 위에 산다면 두 지점의 좌표와 피타고라스 정리를 이용하여 쉽게 거리를 구할 수 있다. 하지만 우리가 사는 지구는 둥글다. 이동이라는 행위를 하고 있는 동안 둥근 지구의 표면 위를 지나게 되기 때문에 당연히 우리의 이동 경로는 곡선 형태가 되며, 경로의 길이를 구하기 것은 단순한 방법으로는 어렵다. 그래서 지구 상의 지점 간 거리를 구하는 다양이 방법이 연구되어 왔다[1].

거리를 구하는 방법의 입력 자료는 좌표(coordinate)이고, 좌표는 좌표체계(coordinate system)의 정의에 따라 다양한 값을 갖는다[2]. 예로부터 인류는 지구 상의 특정 지점의 위치를 정확하게 정의하고자 다양한 좌표체계 방법을 고안하였고, 각각의 좌표체계가 갖는 장단점을 활용하기 위해 변환 방법을 연구하여 왔다[3, 4].

하지만 이러한 연구는 하나의 점에 대한 변환만을 다루기 때문에 디지털 콘텐츠의 활용 측면에서 한계를 갖는다. 최근 위치 관련 디지털 콘텐츠를 다루는 많은 소프트웨어 프로그램에서는 단순하게 거리를 기반으로 하는 좌표체계를 많이 활용한다. 대표적인 예로, 교통 시뮬레이션 소프트웨어 프로그램이 있다[5]. 이는 도로 네트워크를 구축하고 그 기하구조와 운영 조건에 따라 실제 차량이 주행하는 상황을 모사(simulate)하여 도로 설계 타당성 및 교통 운영 효과, 신규 도로 타당성 등을 평가하는데 그 목적성을 갖는다. 주로 신규 주택단지 또는 대규모 상업시설 건설 시 법적으로 요구되는 교통영향평가나 신규 도로 건설, 미래 교통 체계/수단 도입 등에 따른 영향성 평가, 기존 교통체계 문제점 분석 등의 업무에 활용되고 있다.

이러한 교통 시뮬레이션 프로그램에서 주로 사용하는 좌표체계는 거리 기반의 좌표 체계이다. 이는 직교좌표계(Cartesian coordinate system)를 기반으로 x, y축으로 1 미터의 단위 길이를 이용하여 위치 정보를 구성하는 방법으로, 거리에 대한 이해가 직관적이고 현실 반영이 용이하며 복잡한 지리정보체계에 대한 이해가 불필요한 장점을 갖기 때문에 많이 활용되는 추세이다.

최근 들어 Connected vehicle 관련 연구가 활발해지며 교통 시뮬레이션 프로그램에서 현실 도로교통 상황을 모사하고, 여기서 생산된 실시간 데이터를 C-ITS (Cooperative Intelligent Transport System) 센터와 통신함으로써 그 효과를 평가하는 연구가 많이 수행되고 있다. 이 경우 거리 기반 좌표계를 갖는 시뮬레이션 프로그램과 경위도 기반의 좌표계(일반적으로 C-ITS 센터는 정밀도로지도를 이용)를 갖는 센터 간의 좌표 호환성 문제가 발생하기 때문에 교통 시뮬레이션 프로그램에서 생산되는 실시간 좌표(거리 기반 좌표)를 경위도 기반의 좌표계로 변환하는 방법이 필요하다. 이에 본 연구에서는 경위도 좌표를 이용하여 거리를 계산하는 Haversine 공식[6]을 역으로 이용하여 기준점으로부터 상하좌우로 일정 거리만큼 떨어진 지점의 정확한 좌표를 계산하는 Inverse Haversine Method를 개발한다.

다음 장에서는 Haversine Method에 대한 설명과 함께 이를 어떻게 활용하여 Inverse Haversine Method를 만들었는지에 대해 기술한다. 그리고 제안된 방법의 성능을 검증하기 위해 교통 시뮬레이션 프로그램 VISSIM과 구글맵을 활용하여 테스트를 수행하고 그 결과에 대해 논의하며, 마지막으로 결론을 기술한다.

Ⅱ. Inverse Haversine Method의 개발

2-1 Haversine 공식

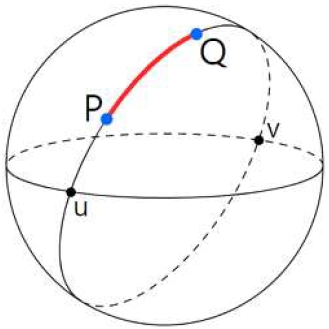
Haversine 공식은 지구를 구(sphere)로 가정하여 두 지점의 좌표(경도, 위도)를 이용하여 지구 표면을 따라 측정한 거리, 즉 대원 거리(great-circle distance)를 구하는데 활용된다. 대원 거리는 그림 2와 같이 구 표면의 가장 짧은 거리를 나타내며, 구 내부를 관통하는 짧은 거리와 구별하여 사용하는 개념이다.

Fig. 2.

Great-circle distance(source: Wikipedia)

두 점 P, Q의 경도(latitude)와 위도(longitude)를 각각 P_x, Q_x, P_y, Q_y라고 하면, 두 지점 간의 거리 d는 다음의 Haversine 공식으로 계산할 수 있다.

$\[ d=2r•\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left(\sqrt{{\text{sin}}^{\text{2}}\left(\frac{Q_x-P_x}{2}\right)+\cos \left(P_x\right)\cos \left(Q_x\right){\text{sin}}^{\text{2}}\left(\frac{Q_y-P_y}{2}\right)}\right) \]$

(1)

여기서 r은 구의 반지름을 나타낸다.

2-2 Inverse Haversine Method

한 점을 중심으로 등거리의 점들을 연결하면 원이 된다. 이는 곧 중심점과 반지름으로 만들어진 고유의 원으로, 구 표면에서 중심점과의 거리가 동일한 점들의 집합을 나타낸다. Haversine 공식의 역(inverse)은 이러한 점들의 집합을 나타낸다.

하지만 본 연구에서 해결하고자 하는 문제는 특정 지점으로부터 일정 거리만큼 떨어진 어떤 지점의 좌표를 찾는 것이다. 이는 뒤에서 언급될 좌표계 변환에서 활용되는 것으로, 좌표계가 다른 계(system)의 어떤 좌표를 지구 표면의 경위도 좌표계로 변환하는 것과 동일한 문제이다.

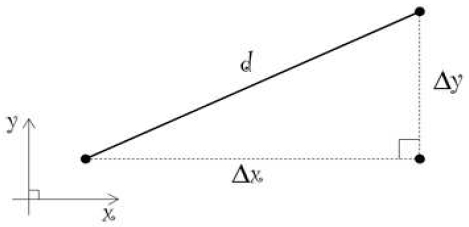
이러한 문제의 해(solution)를 찾기 위해서는 그림 3과 같이 거리를 분할해야 한다. 구의 표면을 평면화하면 거리는 Δx와 Δy로 분할하여 표현할 수 있다. 즉 x축으로 Δx만큼 이동하고, y축으로 Δy만큼 이동하면 거리 d만큼 이동하는 것과 동일하다.

Fig. 3.

Element division of distance

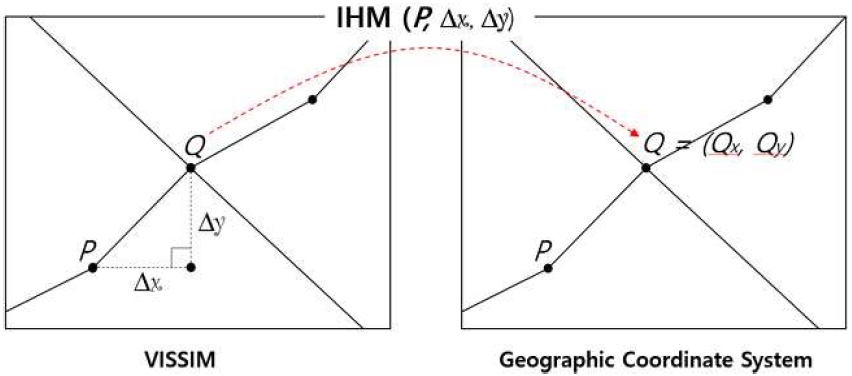
이런 아이디어와 Haversine 공식을 이용하여 Inverse Haversine Method (IHM)를 개발하였다. IHM은 한 지점의 경위도 좌표와 x, y축 이동거리가 주어졌을 때 다른 지점의 경위도 좌표를 구하는 방법이다. 여기서 기준이 되는 지점을 Anchor point (P)라 하고 그 경위도 좌표는 P_x, P_y라 한다. x, y축 이동거리는 각각 Δx, Δy라고 한다.

식 (1)에서의 좌변, 즉 거리값이 주어지면, 우변에는 4개의 변수(P_x, Q_x, P_y, Q_y)가 존재한다. 이 중 P_x, P_y는 이미 주어진 값이기 때문에 실제 변수는 Q_x와 Q_y이다.

방정식의 해를 위한 조건은 변수와 식의 개수가 동일해야하기 때문에 각 축별 이동거리와 변수를 대응시키도록 한다. 즉, 먼저 식 (1)의 좌변에 Δx를 대입하여 우변의 Q_y를 소거하고, 그 다음으로 좌변에 Δy를 대입하여 우변의 Q_x를 소거한다. 좌변에 Δx를 대입하는 것은 y축으로의 이동이 없음을 의미하며 이는 곧 Q_y=P_y를 의미하기 때문에 Q_y가 더 이상 변수가 아닌 상수임을 의미한다. 마찬가지로 좌변에 Δy를 대입하는 것은 Q_x가 상수임을 의미한다. 따라서 두 가지 경우에 대해 각각 계산을 통해 Q_x와 Q_y를 계산할 수 있으며, 그 계산식은 다음과 같다.

$\[ Q_x=P_x+\frac{\mathrm{\Delta }x}{r}\frac{180}{\pi } \]$

(2)

$\[ Q_y=P_y+\frac{360}{\pi }•\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\sin \left(\mathrm{\Delta }y/2r\right)}{\cos \left(P_x\right)}\right) \]$

(3)

여기서 r은 지구 반지름을 나타내고, 단위는 km이다. Δx와 Δy의 단위는 km이고, P_x, P_y, Q_x, Q_y의 단위는 degree이다.

Ⅲ. Inverse Haversine Method의 적용

3-1 개요

본 연구에서는 개발된 Inverse Haversine Method (IHM)의 성능을 검증하기 위해 이종(異種) 좌표 체계 간의 좌표 변환 문제를 활용한다.

GIS(Geographic Information System), ITS(Intelligent Transport System), LBS(Location Based Service)와 같이 공간정보를 활용하는 시스템 또는 서비스는 고유의 좌표 체계를 사용한다. 도로교통 분야에서 많이 활용되는 교통 시뮬레이션 소프트웨어 프로그램은 기본적으로 지도, 즉 공간정보를 이용하기 때문에 자체의 좌표 체계를 이용한다. 대부분의 시뮬레이션 프로그램이 거리 기반의 좌표 체계를 이용하는데, VISSIM도 마찬가지이다. 도로망을 그리기 위해 원점으로부터의 거리를 기반으로 좌표 체계를 구축한다. 즉 노드와 링크를 그리기 위해 사용되는 좌표(x, y)는 원점으로부터의 거리를 의미한다.

반면 GPS(Global Positioning System)는 경위도 좌표 체계(Geographic Coordinate System, GCS)를 이용한다. 따라서 VISSIM의 위치 정보를 GPS 데이터와 매칭하기 위해서는 거리 기반 좌표 체계를 경위도 좌표 체계로 변환해야 한다. 예를 들어 VISSIM에서 차량의 위치와 속성 정보를 추출한 후 거리 기반으로 표현된 위치 좌표를 경위도 좌표로 변환함으로써 GPS 기반의 LBS 시스템(구글맵, 카카오맵 등)과 공유가 가능하다.

따라서 본 연구에서는 그림 4와 같이 VISSIM의 차량 정보를 GCS 좌표체계를 이용하는 TRADOS 센터[7]에 전송하는 시나리오를 가정하여 IHM 방법을 이용한 좌표 체계 변환 시스템을 개발하였다. TRADOS는 레이더를 장착한 차량이 주변 차량을 인식하고 이를 센터에 전송하여 교통 상황을 추정 및 예측하는 시스템으로, 도로망의 표현 및 위치 정보 공유를 위해 경위도 좌표 체계를 이용한다. VISSIM에서 시뮬레이션 결과를 TRADOS 센터에 전송함으로써 현실에서의 구현이 어려운 시장점유율에 따른 효과 분석, 각종 도로교통 이벤트 상황에서의 성능 분석 등이 가능하다.

Fig. 4.

IHM concept applied in VISSIM to GCS coordinate conversion

3-2 IHM 기반 VISSIM 좌표 변환

IHM 방법의 적용을 위해서는 거리 기반 좌표 체계에 Anchor Point가 필요하다. Anchor Point는 좌표 체계 내에서 정확한 경위도 좌표 정보를 갖는 중심점을 의미하며, Anchor Point로부터의 거리를 활용해서 다른 지점의 경위도 좌표를 계산한다.

이를 위해 본 연구에서는 그림 5와 같이 VISSIM 도로망 내 임의의 노드, 실제 도로망에서는 자유로 이산포 IC 중심점을 Anchor Point (P)로 지정하고, 해당 지점의 경위도 좌표(P_x=37.657535, P_y=126.721644)를 입력하였다. 그리고 좌표를 얻고자 하는 지점(Q)을 선정하고, 거리 기반의 좌표 체계를 이용하는 VISSIM 도로망에서 P로부터 Q까지의 거리, Δx, Δy를 계산한 후 식(2)와 (3)을 이용하여 Q의 경위도를 계산하였다.

Fig. 5.

Location of the anchor point (source: Google Map)

제안된 IHM 방법의 성능을 검증하기 위해 임의의 노드 30개를 선정하여 좌표 변환을 수행하였다. 그리고 계산된 경위도 좌표(Q)와 실제 경위도 좌표(Q^R)를 비교하여 그 성능을 검증하였는데, 에러율의 계산을 위해 RMSE (Root Mean Square Error) 인덱스를 이용하였다. 성능 검증 결과는 표 1과 같으며, 이때 지구 반지름 r은 6378.137 km를 이용하였다.

Table 1.

The result of IHM coordinate conversion

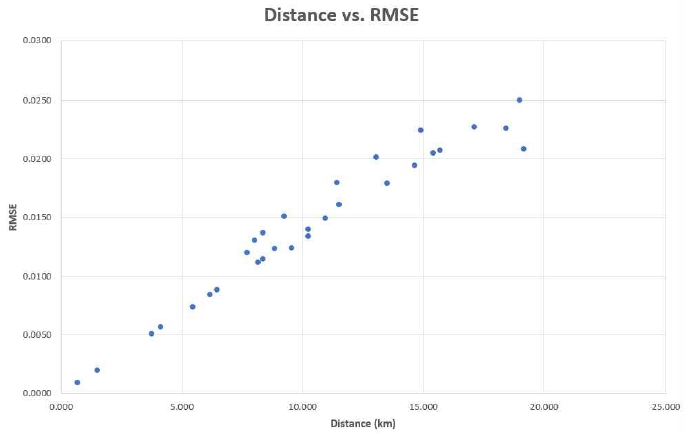
검증 결과, 대부분의 좌표 변환에서 RMSE는 0.025 이하로 나타남에 따라 변환이 잘 된 것으로 판단된다. 특히 첫 번째 좌표 변환의 경우 RMSE가 0.0009로, 거의 오차가 없는 것으로 나타났다. 하지만 Δx와 Δy가 점점 증가함에 따라 오차율이 증가하기 때문에 향후 이에 대한 보안책이 필요할 것으로 판단된다(그림 6).

Fig. 6.

Distance vs. RMSE

Ⅳ. 결 론

본 연구에서는 위치 좌표를 아는 어떤 지점으로부터 동서 및 남북 방향으로 일정 거리만큼 떨어진 지점의 좌표를 계산하는 Inverse Haversine Method (IHM)를 개발하였다. 이를 위해 Haversine 공식에 거리 요소 분할 개념을 적용하여 역함수를 유도함으로써 대상 지점의 경도와 위도를 각각 계산하는 두 개의 식을 제안하였다. 개발된 IHM을 이용하여 거리 기반의 좌표체계를 사용하는 VISSIM 도로망의 노드 좌표를 GCS 좌표 체계로 변환하는 테스트를 수행하였고, 그 결과 IHM이 좌표 변환을 성공적으로 하는 것으로 나타났다. 다만 대상 지점이 Anchor Point와 멀어질 때 발생하는 오차율 증가는 향후 해결해야 할 문제로 판단된다.

Acknowledgments

본 연구는 2019년 한국건설기술연구원 주요사업(차량센서 기반 주행환경 관측·예측·안전운행 도로기술 개발, 과제번호: 20190149-001)의 연구비 지원에 의해 수행되었습니다.

참고문헌

• Chamberlain, R. G., “Great circle distance between 2 point, ” http://www.movable-type.co.uk/scripts/gis-faq-5.1.html, , access in Sep., 2019.
• Decker, B. Louis, World geodetic system 1984, Defense Mapping Agency Aerospace Center St Louis Afs Mo, 1986.
• Lin, K.C. and Wang, J., “Transformation from geocentric to geodetic coordinates using Newton's iteration”, Bulletin Geodesique, Vol. 69, No. 4, pp.300-303, 1995. [https://doi.org/10.1007/BF00806742]
• Featherstone, W.E. and Claessens, S.J., “Closed-form transformation between geodetic and ellipsoidal coordinates”, Studia geophysica et geodaetica, Vo. 52, No. 1, pp.1. 2008. [https://doi.org/10.1007/s11200-008-0002-6]
• Yang, I. & Jeon, W-H, “Development of lane-close model using micro simulation”, Journal of Digital Contents Society, Vol. 19, No. 11, pp. 2131-2137, 2018.
• Sinnott, R.W., “Virtues of the Haversine”, Sky and Telescope, Vol. 68, No. 2, pp.159, 1984.
• Yang, I. & Jeon, W-H, “Development of traffic state observation technology using automotive sensors,” Journal of Digital Contents Society, Vol. 19, No. 11, pp. 2131-2137, 2018. [https://doi.org/10.9728/dcs.2018.19.11.2131]