[ Article ]

Journal of Digital Contents Society - Vol. 20, No. 6, pp.1235-1241

ISSN: 1598-2009 (Print) 2287-738X (Online)

Print publication date 30 Jun 2019

Received 20 May 2019 Revised 20 Jun 2019 Accepted 25 Jun 2019

DOI: https://doi.org/10.9728/dcs.2019.20.6.1235

DANN : 이산 산술 신경망

박재흥¹ ; 김호¹ ; 서영건²^{, *}

1경상대학교 컴퓨터과학과
2경상대학교 컴퓨터과학과, 대학원 문화융복합학과

DANN : Discrete Arithmetic Neural Networks

Jae Heung Park¹ ; Ho Kim¹ ; Yeong Geon Seo²^{, *}

1Dept. of Computer Science, Gyeongsang Nat’l University, Gyeongnam 52828, Korea
2Dept. of Computer Science and CCBM of Graduate School, Gyeongsang Nat’l University, Gyeongnam 52828, Korea

Correspondence to: ^*Yeong Geon Seo Tel: +82-55-772-1392 E-mail: young@gnu.ac.kr

Copyright ⓒ 2019 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

딥러닝은 기계학습의 일종으로, 입력값과 결과값 사이의 적당한 함수를 역전파 알고리즘을 통해 구한다. 그러나 딥러닝은 훈련값의 패턴에 대해 추론하기보단 훈련값을 외우려는 현상이 짙고, 이는 훈련값에서 벗어난 데이터에 대해선 추론능력이 크게 떨어지는 오버핏(overfit) 현상을 보인다. 이 문제를 해결하기 위해, 본 논문에서는 실수 공간의 입력값과 출력값을 부울 공간으로 한정시킴으로써 문제를 해결하려는 Discrete Arithmetic Neural Networks (DANN)라는 알고리즘을 제시한다. DANN은 입력값과 출력값이 부울 공간으로 한정될 수 있는 경우, 부울 대수만을 이용하여 딥러닝을 설계할 수 있음을 보인다. 다만 부울 대수만으로는 역전파 알고리즘을 구현할 수 없으므로, 실수(float)를 적절히 이용하여 부울 연산을 모방한다. 결과적으로 이것이 부울 공간을 사용했을 때 LSTM 등 기존의 딥러닝 알고리즘을 사용했을 경우보다 성능이 우수함을 보인다.

Abstract

Deep learning is a kind of machine learning, and a proper function between the input value and the result value is obtained through the back propagation algorithm. However, deep running is a phenomenon that attempts to memorize the training value rather than deducing the pattern of the training value, which shows overfitting phenomenon that the reasoning ability is greatly reduced for the data that deviates from the training value. To solve this problem, we propose an DANN to solve the problem by limiting input and output values of real space to Boolean space. DANN shows that if the input and output values can be limited to boolean spaces, we can design a deep running using only Boolean algebra. However, since Boolean algebra alone can not implement a back propagation algorithm, it imitates a Boolean operation using the float appropriately. As a result, it shows better performance when using Boolean space than using existing deep running algorithms such as LSTM.

Keywords:

DANN, Discrete Arithmetic Neural Networks, Deep Learning, Machine Learning, Boolean Space

키워드:

DANN, 이산 산술 신경망, 딥 러닝, 기계 학습, 부울 공간

Ⅰ. 서 론

딥러닝은 입력값과 결과값 사이의 적당한 함수를 인간의 개입 없이 역전파 알고리즘을 통해 구하는 범용 기계학습의 일종이다[1]. 이를 응용한 딥러닝 기술은 영상 처리, 음성 처리, 자연어 처리 등 기계학습을 필요로 하는 분야에서 활발히 연구되고 있다. 특히, 시계열적인 값이나 패턴을 많이 보유한 데이터에 대해 높은 수준의 학습 능력을 보인다. 그러나, 딥러닝은 훈련 시에 훈련값의 패턴을 추론하기보다는 암기하려는 경향을 보인다. 이는 훈련값에서 벗어난 데이터에 대해 패턴을 찾지 못해 의미없는 값을 출력하는데 이를 오버핏(overfit) 되었다고 말하고, 활발히 연구되어 드롭아웃(dropout) 등의 방법이 제안되었다[2].

Fig. 1.

Errors on evaluating data outside the learning range

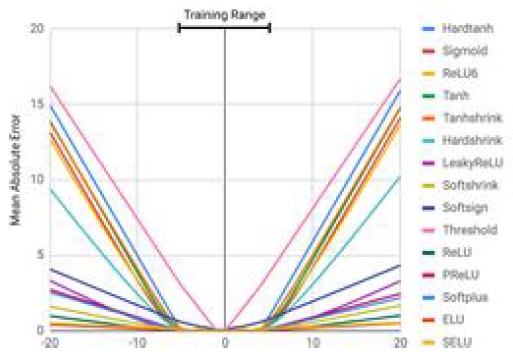
최근의 Google의 논문에서는 학습에 사용된 데이터셋에서 크게 벗어난 입력값이 들어오면 큰 폭의 오차가 발생하는 현상을 진단했다[3]. ReLU(Rectified Linear Unit), Leaky ReLU, PReLU(Parametric ReLU) 등 많은 비선형 함수들을 이용하여 다층 퍼셉트론을 설계하였을 때, 이는 항등함수를 제대로 학습해내지 못했다[4-6]. 저자들은 그 이유를 외삽오류(Extrapolation Error)가 발생하기 때문이라고 주장한다. 여기서는 이 문제를 해결하기 위한 방법으로 Neural Arithmetic Logic Units을 제시했다. 이 방법을 이용하면 실수 간의 사칙연산과 지수로그 연산 등을 딥러닝 내에서 문제없이 사용할 수 있다고 주장한다. 또한 저자들은 기존의 신경망 알고리즘들에 비해 외삽오류에 강하다고 주장한다. 그러나 입력값과 출력값이 산술관계에 있음을 가정한다. 즉, 항등함수나 입력값 간의 덧셈 등의 관계에 있는 경우 높은 정확도를 보이나, 모든 일반적인 경우에 대해 적용할 수는 없다고 설명한다.

본 논문에서는 이러한 일반적인 경우에서의 오버핏 문제가 발생하는 이유를 딥러닝이 입력값과 출력값의 범위를 제한하지 않았기 때문으로 가정하였다. 그리고 이를 입증하기 위해, 오직 0과 1의 바이너리와 논리 게이트만 사용하는 모델을 생성하는 딥러닝 알고리즘을 제안한다. 그리고 LSTM(Long Short Term Memory)과 비교하여 32비트 직렬가산기를 구현했을 때, 제안한 알고리즘이 대조군과 달리 오차가 전혀 없이 학습될 수 있음을 보인다. 논문의 구성은 2장에서 관련 연구에 대해 살펴보고, 3장에서 제안 방법의 설계와 4장에서 제안 방법의 유효성을 검증한다.

Ⅱ. 기존의 연구 방법

2-1 XNOR 게이트를 이용한 시도

참고문헌 [7]에는 가중치를 학습 중에 +1 혹은 -1로 강제하여 학습시키는 BNN(Binarized Neural Networks) 알고리즘을 제안하였다. 이 방법은 XNOR과 popcount(바이너리 벡터의 맨해튼 거리) 연산을 모방하여 파라미터를 학습시킨다. 학습 중에 가중치를 바이너리로 변환시키는데, 이에 해당하는 함수 sign은 다음과 같다.

s i g n x = + 1 i f x ≧ 0, - 1 o t h e r w i s e,

(1)

단, 바이너리 가중치를 이용하여 입력값에 행렬곱 하는 경우, 해당 학습 모델은 학습 속도가 늦는 뿐더러, 각 가중치가 학습 전반에 미치는 영향이 큰 것으로 판단된다. 때문에 정규화하는 과정이 필수인데, 이때 사용하는 BN (Batch Normalization) 알고리즘은 다음과 같다[8].

Fig. 2.

Batch normalization(ϵ is a sufficiently small number)

BN을 취한 이후, 마지막 레이어를 제외한 출력값에 sign 함수를 취해준다. 마지막 레이어를 통과하여 결과값을 얻은 후, 역전파 알고리즘을 수행하여 기울기를 구한다. 이때 기울기는 바이너리 값이 아닐 수 있다. 구한 기울기 값을 바탕으로 ADAM(ADAptive Moment Estimation) 알고리즘을 활용해 파라미터를 업데이트한다[9]. 마지막으로, 파라미터의 값에 다음과 같은 clip 함수를 취한다.

c l i p x = - 1 x < 1 x x ≦ 1 + 1 x > 1

(2)

2-2 MLP

일반적으로, 딥러닝에서의 다층 퍼셉트론 MLP (Multilayer Perceptron)는 입력값이 여러 개의 단층 퍼셉트론과 비선형함수 등을 통과하게 설계된 알고리즘을 말한다. 여기서 단층 퍼셉트론 Dense(x)는 입력값 x, 가중치 행렬 W, 편향값 b에 대해 다음과 같은 함수를 통과하는 알고리즘을 말한다.

D e n s e x = x W + b

(3)

단층 퍼셉트론을 통과한 출력값은 입력값과 선형 관계에 놓이는데, 이를 ReLU와 같은 비선형함수를 통과하게 하여 선형성을 지울 수 있다. 그리고 이 과정을 여러 번 거치는 것이 MLP가 된다. 최근에는 MLP를 다른 딥러닝 모델의 일부로 사용하는 추세이다.

2-3 LSTM

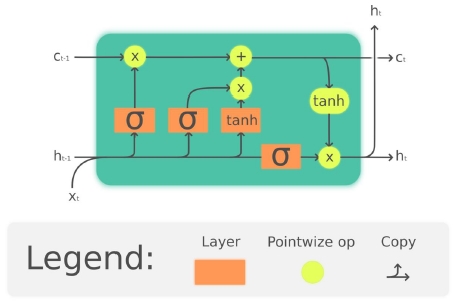
LSTM에서는, 순환 모델의 장기 의존성 문제를 해결하기 위해 LSTM 이라는 순환 인공 신경망 (RNN)을 제안하였다[10]. 이 방법은 시계열 데이터의 서로 멀리 떨어진 값 간의 관계를 학습하기 힘들어하는 문제를 해결하기 위해, 입력 게이트, 출력 게이트, 망각 게이트를 도입하여 메모리를 선별적으로 갱신한다.

Fig. 3.

Outline of LSTM processing time series data

LSTM에서 입력값 x에 대해 입력 게이트 i, 출력 게이트 o, 망각 게이트 f는 각각 다음과 같다.

f t = σ g W f x t + U f h t - 1 + b f i t = σ g W i x t + U i h t - 1 + b i o t = σ g W o x t + U o h t - 1 + b o

(4)

여기서, W, U는 가중치 행렬, b는 편향값, σ는 시그모이드 함수, t는 time step이다. 그리고 h는 LSTM의 은닉 상태 벡터이자 출력값으로, 그 수식은 다음과 같다.

h t = o t ∘ σ h c t

(5)

여기서, c는 셀 상태 벡터로, 그 수식은 다음과 같다.

c t = f t ∘ c t - 1 + i t ∘ σ c W c x t + U c h t - 1 + b c

(6)

여기서 c₀ = 0, h₀ = 0이다.

Ⅲ. 이산 산술 신경망 설계

본 장에서는 입력값, 출력값, 가중치 등 모든 값들이 0 혹은 1로 고정되도록 학습시키는 딥러닝 알고리즘인 이산 산술 신경망(Discrete Arithmetic Neural Networks : DANN)을 제안한다. DANN에 사용되는 모델은 크게 두 가지가 있다. 하나는 BLL(Binary Linear Layer)이고, 다른 하나는 RBL(Recurrent Binary Layer)이다.

Fig. 4.

Outline of BLL

3-1 BLL

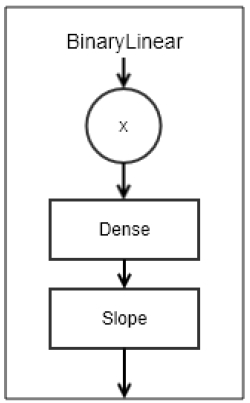
BLL은 입력값에 선형변환 가중치 W를 행렬 곱한 후, Slope 함수를 취해준다.

Fig. 5.

Graph of Slope function

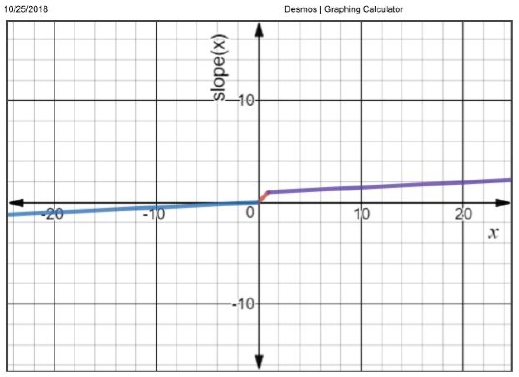
여기서 Slope 함수는 HardTanh 함수를 누수(leaky)하게 구현한 것으로, 한쪽으로 크게 치우친 값이 역전파를 통해 학습이 진행되도록 한다. Slope 함수는 입력값 x, 기울기 α에 대해 다음과 같다.

S l o p e α, x = α x x α x - 1 + 1 x < 0 0 ≦ x ≦ 1 x > 1

(7)

다만, 가중치 또한 0 혹은 1로 고정되어야 한다. 여기서는 가중치에 sigmoid 함수를 취하여 그 역할을 모방하였다. 따라서, BLL을 수식화하면 다음과 같다.

B L L α, x, W = S l o p e α, x * s i g m o i d W

(8)

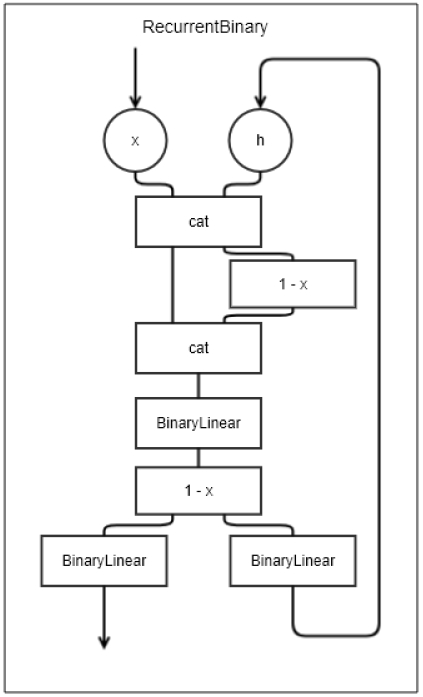
3-2 RBL

DANN에 사용되는 두 번째 모델로는 RBL이며, BLL에 기억 능력을 더한 것으로, 이전의 행동을 0 혹은 1로 기억해 두었다가, 새로운 입력이 들어오면 이에 반영한다. RBL를 이용하면 시계열 데이터에 대한 처리가 가능하다. RBL의 각 시계열 입력값의 뉴런들은 순서를 섞을 수 있다고 가정한다. 또한 이를 구현하는 함수를 shuffle 함수라고 가정하겠다.

RBL을 활용하려면, 먼저 메모리 h를 0으로 초기화시킨다. 메모리는 이전 행동의 형태를 기억했다고 간주한다. 그리고 x_t와 h_t을 결합하여 shuffle 함수를 취해준 a_t을 만들고, 또 a_t과 1 - a_t을 결합하여 b_t를 만든다. 이를 통해 b_t는 x_t, x_t´, h_t, h_t´을 모두 표현할 수 있다. 이후 BLL에 b_t를 입력하여 c_t을 만들고, 여기서 k_t = 1 - c_t을 구한다. 여기서 k_t는 b_t에 대한 부울 함수의 관계를 가진다. 마지막으로, k_t를 BLL에 입력하여 각각 y_t과 h_t₊₁을 구한다.

a t = s h u f f l e c a t x t, h t b t = c a t a t, 1 - a t c t = B L L α, b t, W 1 k t = 1 - c t y t = B L L α, k t, W 2 h t + 1 = B L L α, k t, W 3

(9)

Fig. 6.

Outline of RBL

Ⅳ. 실험 및 평가

4-1 실험 방법

제안된 방법의 성능을 평가하기 위해, 32비트의 부호 없는 두 정수의 덧셈을 출력하는 모델을 구현한다. 두 입력값 x,y가 기댓값 z에 대해 다음의 관계(식 10)를 가진다.

B = 0,1, x ∈ B 32, y ∈ B 32 z = a d d x, y

(10)

식 (10)에서 add는 두 부울 벡터 x,y를 전가산기를 이용하여 덧셈 연산하는 함수를 의미한다. 다음 실험의 평가를 위한 오차 loss는 제곱평균오차를 사용하며, 기댓값 z와 예측값 z´에 대해 다음의 관계를 가진다.

l o s s = z - z' 2

(11)

실험에 사용될 데이터 셋으로는 훈련 데이터 셋, 평가 데이터 셋이 있다. 훈련 데이터 셋은 0부터 10,000 사이의 세 개의 수 x,y,z의 쌍 중 10,000 개를 가진다. 평가 데이터 셋은 100,000부터 1,000,000 사이의 세 개의 수 x,y,z의 쌍 중 1000 개를 가진다. 본 실험은 [Ubuntu 18.04.1 LTS (Bionic Beaver)] 운영체제, 64GB 메모리, CPU로 [Intel(R) Core(TM) i7-8700K CPU @ 3.70GHz]를 사용한다.

4-2 실험 그룹 정의

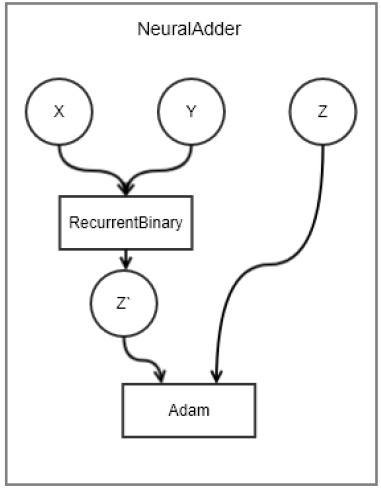
DANN의 RBL을 이용하여 실험군 모델은 그림 7에 나타내었다. 여기서 add = RBL이며, 학습은 Adam을 이용하여 훈련 데이터 셋에 대해 10개 배치 단위로 학습한다. 만약 loss가 0.001 이하로 감소할 경우, 데이터 셋을 모두 학습하지 않고 마친다.

Fig. 7.

Outline of experimental group model

4-3 비교 그룹 정의

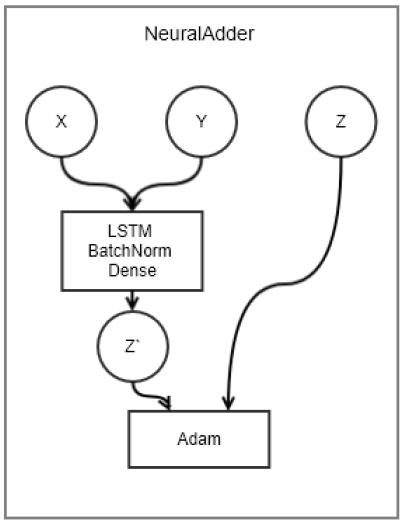
실험의 비교를 위한 대조군은 LSTM과 MLP를 이용한다. 그림 8은 LSTM 모델 개요도를 보이고 있고, 여기서 add는 순서대로 LSTM, BatchNorm, Dense 레이어를 통과하는 것을 의미한다. 학습은 Adam을 이용하여 훈련 데이터 셋에 대해 10개 배치 단위로 학습한다. 만약 loss가 0.001 이하로 감소할 경우, 데이터 셋을 모두 학습하지 않고 마친다.

Fig. 8.

Outline of comparative group(LSTM) model

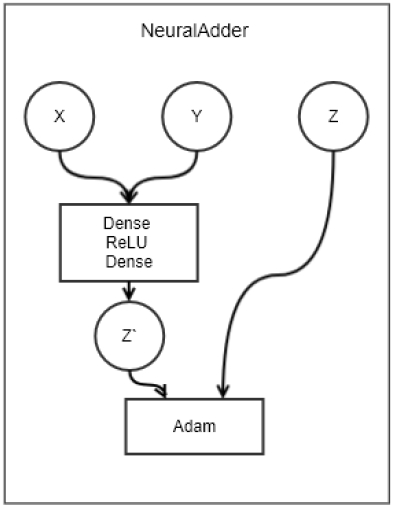
그림 9는 MLP 모델 개요도를 보이고 있고, 여기서 add는 순서대로 Dense, ReLU, Dense 레이어를 통과하는 것을 의미한다. 학습은 Adam을 이용하여 훈련 데이터 셋에 대해 10개 배치 단위로 학습한다. 만약 loss가 0.001 이하로 감소할 경우, 데이터 셋을 모두 학습하지 않고 마친다.

Fig. 9.

Outline of comparative group(Dense) model

4-4 성능 평가

실험군과 대조군의 성능을 평가하기 위해, 두 척도를 이용하기로 한다. 첫 번째로 평가 데이터 셋의 loss를 단순 비교한다. 두 번째로 예측값의 정확도를 측정한다. 정확도는 예측값과 기댓값의 각 자릿값의 맨해튼 거리가 0.5 이하일 때 1점, 아닐 때 0점을 주어 전체 자릿값에서 그 평균을 구한 것이다. 각 척도는 위의 실험을 30번 반복하여 그 평균을 낸 값을 기록한다.

실험군과 대조군 모두 훈련 데이터 셋의 loss는 학습이 중단되는 지점인 0.001에 접근하였다. 표 1은 위의 평가 방법을 토대로 각 모델의 성능을 평가한 것이다. 표에서 DANN은 실험군을, LSTM은 LSTM을 이용한 대조군을, Dense는 Dense를 이용한 대조군을 의미한다. 제안 방법은 100%의 평균 정확도를 가졌다. 반면 LSTM과 Dense는 0%의 평균 정확도를 가졌다. 결론적으로 제안 방법은 학습이 정상적으로 이루어졌으나, 대조군의 경우 학습이 이루어졌다고 볼 수 없었다.

Table 1.

Experimental Results

Ⅴ. 결 론

본 연구는 딥러닝 모델이 훈련값의 패턴에 대해 추론하기보단 훈련값을 외우려는 현상을 진화하기 위해 DANN 이라는 알고리즘을 제시하였다. 이는 훈련값에서 벗어난 데이터에 대해서는 추론능력이 크게 떨어지는 오버핏 현상을 해결하기 위해, 실수 공간의 입력값과 출력값을 부울 공간으로 한정시키는 접근을 하였다. DANN은 입력값과 출력값이 부울 공간으로 한정될 수 있는 경우, 부울 대수만을 이용하여 딥러닝을 설계할 수 있음을 보였다. 본 연구에서 제안한 방법을 사용했을 때, LSTM 등 기존의 딥러닝 알고리즘으로 학습이 진행되지 않던 문제를 해결할 수 있음을 보였다.

References

Yann Lecun, Yoshua Bengio, and Geoffrey Hinton, “Deep learning“, Nature, 521, p436-444, (2015).
Nitich Srivastava, Georey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov, “Dropout: A Simple Way to Prevent Neural Networks from Overfitting”, Journal of Machine Learning Research, 15, p1929-1958, (2014).
Andrew Trask, et al., “Neural Arithmetic Logic Units”, (2018).
Saito Goki, ReLU Deep Learning from Scratch, p76, (2017).
Himanshu Sharma, Activation Functions : Sigmoid, ReLU, Leaky ReLU and Softmax basics for Neural Networks and Deep Learning, http://medium.com.
Kaiming He, and et al., PReLU : Delving Deelp into Rectifiers : Surpassing Human-Level Performance on ImageNet Classification, (2015).
M. Courbariaux, and Y. Bengio, “Binarized neural networks: Training deep neural networks with weights and activations constrained to +1 or −1.”, http://arxiv.org/abs/1602.02830 Feb.), (2016.
Sergey Ioffe, and Christian Szegedy, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift“, Proceedings of the 32nd Int’l Conference on Machine Learning, 37, p1-15, Mar.), (2015.
Diederik P. Kingma, and Jimmy Ba, “Adam: A Method for Stochastic Optimization”, ICLR 2015, p1-15, Jan.), (2015.
F. A. Gers, J. Schmidhuber, and F. Cummins, “Learning to forget: continual prediction with LSTM”, 9th International Conference on Artificial Neural Networks: ICANN '99, p850-855, (1999). [https://doi.org/10.1049/cp:19991218]