CUDA 기반 병렬 6차원 shifted sort를 이용한 근사 k-최근접 이웃 정보 검색 구현
Copyright ⓒ 2019 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문에서는 shifted sort 기반 병렬 kANN(k-Approximate Nearest Neighbor) 기법을 다차원(n > 3) 벡터로 확장하기 위한 중간 단계로서 CUDA에서 지원하는 네이티브 자료형 중 가장 큰 크기를 제공하는 128비트 크기의 uint4 자료형을 이용한 6차원 shifted sort 기반 병렬 kANN의 구현 및 그 결과를 논의한다. 이러한 목표를 달성하기 위해서 6차원 Morton 코드 생성 알고리즘을 구현하였으며 테스트를 위해 3차원 삼각형 mesh에서 6차원 벡터의 추출 방안과 그 기하학적인 의미에 대해 분석한 후 기존 방식과 실행 결과를 비교하였다. 실행 결과 3차원에서 6차원으로 확장한 경우에도 실행 시간 상의 변화는 상대적으로 적었으며 향후 6차원 이상의 다차원 벡터로 shifted sort 기반 병렬 kANN을 확장하기 위한 기본적인 정보를 확보할 수 있었다.
Abstract
This paper presents a way to implement six dimensional shifted sort based parallel kANN with the 128 bit uint4 data type and comparison results of the proposed method. This research is an intermediate process to improve shifted sort based parallel kANN method to handle more general vectors with more than six dimensions. For this goal, the author implements six dimensional Morton code and proposes the method to extract six dimensional vectors from three dimensional triangle meshes. Also, the author discusses the geometrical meaning of six dimensional extension for the three dimensional triangle meshes. As a result, the time difference between the three dimensional version and six dimensional one is relatively small. From this result, the author has gained some insight to expand the proposed method to larger vectors.
Keywords:
Six dimensional Morton code, Parallel shifted sort, CUDA, GPU, Approximate nearest neighbor search키워드:
6차원 Morton 코드, 병렬 shifted sort, CUDA, GPU, 근사 최근접 이웃 정보 검색Ⅰ. 서 론
1-1 문제 정의 및 연구 배경
k 근사 최근접 이웃 정보 검색(kANN, k-approximate nearest neighbor search)[1]은 d 차원 벡터 n개로 구성되는 데이터 벡터 집합 P = {p1, p2,....pn}와 질의 벡터 q (즉, pi, q∈ Rd, 1≤ i≤n)에 대해 일정한 오차를 허용하면서 질의 벡터 q에 가장 가까운 거리에 있는 k개의 데이터 벡터를 구하는 알고리즘으로 정의된다. 이 때 거리는 임의의 Minkowski Lm distance metric[1]으로 정의된다. 즉,
| (1) |
특히 식 (1)에서 m=2일 때 거리는 유클리드 거리가 된다.
이러한 벡터 간의 최근접 이웃 검색 기술은 데이터베이스 검색[2], 구간 검색[3], 3차원 공간 정보 처리[4, 5] 등 다양한 목적으로 활용된다.
본 논문에서는 3차원 벡터를 위해 구현된 기존 연구[4, 5]를 확장하여 6차원 벡터에 대해 GPU 아키텍처에 최적화된 k 근사 최근접 이웃 정보 검색 알고리즘을 제안하고 구현 결과를 논의한다. 제안하는 연구는 보다 일반적인 길이(d > 3)의 벡터로의 구현을 위한 예비 단계로 볼 수 있으며 GPU 아키텍처에서 네이티브 자료형 수준에서 처리 가능한 최대 크기의 자료형인 128비트 uint4형에 기초해서 6차원 Morton 코드를 구성하고 기존 연구[4, 5]에서 제안한 병렬 kANN 기법을 확장한다.
제안하는 기법은 일반적인 길이를 가지는 벡터로의 확장을 위한 예비 조사를 수행하기 위한 연구로 볼 수 있다. 특히 본 논문에서는 6차원 kANN 기법을 활용해서 일반적으로 AABB (Axis Aligned Bounding Box) [6] 형태로 표현되는 3차원 공간 상의 범위(interval)를 6차원 벡터로 표현하고 이 6차원 벡터 사이의 Euclidean 거리의 기하학적인 의미에 대해 논의한다.
1-2 기존 연구
Chan[7]과 Arya et al.[8]은 k개의 최근접 벡터를 정확하게 구하지 않고 일정한 오차를 허용해서 근사화된 k개의 최근접 벡터를 구할 경우 실행 시간 측면에서 상당한 개선을 실현할 수 있음을 증명하였다. 이러한 오차를 허용하는 k개의 최근접 이웃 벡터의 검색 문제는 다음과 같이 정리할 수 있다[8].
| (2) |
이 때 식 (2)에서 p*는 질의 벡터 q에서 실제로 가장 가까운 최근접 벡터를 의미하며 위 식을 만족시키는 벡터 p는 q의 ‘(1+ϵ) 근사 최근접 이웃 벡터((1+ϵ) -approximate nearest neighbor)’라고 정의한다. 또한 ϵ 값이 무한하게 큰 경우를 허용한다면 근사 최근접 검색의 효용성이 없기 때문에 ϵ<1로 한정하는 것이 일반적이다. 본 논문에서 다루는 k 근사 최근접 이웃 정보 검색 문제(kANN)는 식 (2)의 조건을 만족시키는 데이터 벡터 p를 사용자가 원하는 개수인 k개만큼 구하는 것이 목적이다.
Li et al.[9]은 Chan의 증명[8]에 기초해서 GPU 상에서 shifted sort에 기초한 kANN 알고리즘을 제안하였다. 이 연구에서는 일반적인 길이의 벡터에 대한 GPU 상의 구현을 위한 유사 코드를 제시하였으나 GPU 아키텍처 측면에서의 구현 세부 사항은 다루지 않았다. Park[10]은 Li et al.[9]에서 제안한 알고리즘을 구현하기 위한 기본 구성요소인 Morton code 변환의 의미를 분석하였으며 Park[4]과 Kim et al.[5]은 실제 CUDA(Compute Unified Device Architecture)[11]에서 3차원 기하 정보 애플리케이션을 위한 구현에서 최신 GPU 하드웨어 아키텍처 및 물리적 실행의 최소 단위인 warp 구조에 최적화된 방법을 제안하고 기존 GPU 기반 kd-tree와의 비교 분석을 수행하였다.
본 연구에서는 기존 연구[4,5]를 확장하여 CUDA에서 표현할 수 있는 최대 크기의 자료형인 128 비트 uint128 타입을 이용해서 6차원 Morton 코드를 구성하고 shifted sort 방식에 기초한 kANN을 구현한다. 본 논문의 근간을 이루는 shifted sort 기법과 3차원 기하 정보에 대한 kANN 병렬 처리와 관련된 세부 내용은 내용 상의 중복을 피하기 위해 특별히 필요한 경우에 한해서만 본 논문에서 간략하게 서술하고자 한다. 자세한 세부 정보는 해당 문헌[4, 5, 7, 9]을 참고한다.
Ⅱ. 이 론 및 구 현
2-1 6차원 벡터 표현을 위한 128 비트 Morton 코드 구현
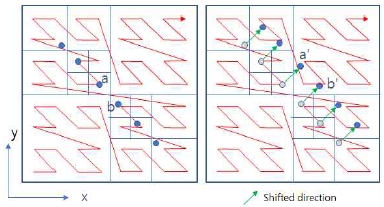
그림 1[5]에서는 2차원 벡터 공간에서 데이터 및 질의 벡터(파란색 점)이 존재하는 범위(좌우 그림에서 주변의 파란색 사각형 외곽선)에 대해 공간 채움 곡선(space-filling curve)으로 Morton 코드(빨간색 선)를 적용한 후(왼쪽 사각형) shifted sort [7] 알고리즘을 적용하여 질의 벡터와 데이터 벡터를 우상향 방향으로 shift 시킨 결과(오른쪽 사각형)를 제시하고 있다.
Morton code shifting direction in 2D space [5]
그림 1에서 확인할 수 있는 것처럼 2D Morton 코드는 본질적으로 quadtree [12]의 탐색 구조와 동일하며 3D Morton 코드는 octree [13]의 탐색 구조와 동일하다. 또한 임의의 d 차원(d>3) 벡터에 대해서도 Morton 코드를 적용할 수 있으며 각 축(즉, 벡터의 각 차원)에 대해 독립적으로 이진 탐색을 적용한 탐색 구조라고 볼 수 있다. Karras는 3차원 벡터의 Morton 코드를 32비트 데이터형(unsigned int)으로 표현하는 방법을 제안하였다[14]. 이 방식은 각 차원 당 10비트를 할당하고 나머지 2비트에 추가 정보를 저장할 수 있다. 일반적으로 본 연구의 대상이 되는 d 차원의 질의 벡터와 데이터 벡터는 [0, 1]d 공간의 hypercube에 포함되도록 균일화(normalize)가 가능하다. 이렇게 균일화할 경우 각 차원의 값은 [0, 1] 구간에 포함되며 IEEE 754 표준에 의거한 float 변수 형식[15]으로 표현하면 23비트 가수(fraction) 부분에 대부분의 정보가 저장된다. 따라서 Keras의 방식대로 각 차원 당 10 비트만을 할당할 경우 float 데이터형으로 표현 가능한 정보의 정밀도가 크게 감소한다[10].
이 문제를 해결하기 위해서 64비트 변수 형식(unsigned long long)으로 3차원 벡터의 Morton 코드를 생성하는 방법이 제안되었다[9]. 3차원 벡터 하나에 64비트를 할당할 경우 각 차원 당 21비트 할당이 가능하고 나머지 1비트를 특정한 목적에 할당할 수 있다. S. Li et. al의 연구[9]에서는 이 여분의 비트를 질의/데이터 벡터 구분 목적으로 사용하였다.
본 논문에서는 S. Li et. al의 연구를 확장하여 128비트 변수형(uint4)에 기초한 6차원 벡터 Morton 코드를 구현하였다.
표 1에서는 CUDA 표준 라이브러리인 vector_types.h에 정의된 uint4 데이터형을 제시하였다. CUDA C 확장 키워드(__device_builtin__ __builtin_align__(16))를 제외하면 기본적으로 C/C++ 표준 struct 타입임을 확인할 수 있다.
Definition of CUDA standard uint type (in “vector_types.h”)
표 2에서는 128비트 Morton 코드 연산을 위한 실제 CUDA 코드를 제시한다. 이 코드는 Ⓐ 21비트 패턴 변환([10]의 2.1절 참고), Ⓑ 128비트 길이의 uint4 변수에 할당하기 위한 상대적인 6비트 shift 이동(그림 2참고), Ⓒ 128 비트 변수형에 대한 bitwise OR 연산 수행(표 3 참고)을 여러 스레드가 병렬로 실행한 후 128비트 Morton 코드를 반환한다. 기존 64비트 Morton 코드[10] 루틴과 다른 부분은 그림 2에서 제시한 6비트 shift 이동 복제 부분이며 이 루틴은 향후 임의의 d 차원으로의 확장을 위한 기초적인 코드로 활용할 계획이다.
morton6D128 function
The bit placement patterns of expandBits128XX functions in Table 2
bitwOR function
2-2 3차원 벡터 정보의 6차원 벡터로의 확장
지금까지 논의한 방식을 바탕으로 기존 3차원 병렬 shifted sort 기반 kANN 알고리즘[4]을 6차원으로 확장하였다. CUDA 하드웨어에 최적화된 기존 알고리즘[4]을 기반으로 하고 데이터 차원만 확장하였기 때문에 구현 가능한 k 값은 CUDA에서의 물리적 동시 실행 단위인 warp 크기의 1/2인 16개까지 가능하다(k = 2, 4, 8, 16).
본 논문에서는 이 병렬 알고리즘으로 실행 속도 테스트를 수행하기 위해서 3차원 공간 내 질의 벡터와 근사적으로 가장 가까운 삼각형을 찾는 문제 상황을 가정한다. 이 알고리즘에 투입할 6차원 데이터를 위해 3차원 mesh 데이터를 구성하는 각 삼각형 face의 AABB를 계산하고 이 AABB의 최소점과 최대점으로 6차원 벡터를 구성한다. 3차원 mesh 정보로부터 6차원 벡터를 구성하는 방식은 두 가지를 생각할 수 있다.
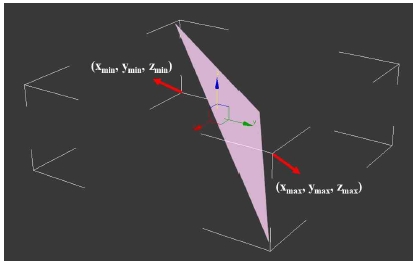
첫 번째 방식(그림 3)에서는 AABB의 최소점 좌표가 (xmin, ymin, zmin)이고 최대점 좌표가 (xmax, ymax, zmax)이라면 3차원 공간에서 interval 또는 hypercube 에 해당되는 이 AABB는 6차원 벡터 (xmin, ymin, zmin, xmax, ymax, zmax)으로 표시할 수 있다. 이러한 형식에서 3차원 질의 점 (x, y, z)는 6차원 벡터 (x, y, z, x, y, z)로 표현 가능하다.
The first approach to convert a triangle face in 3D space to a 6D vector
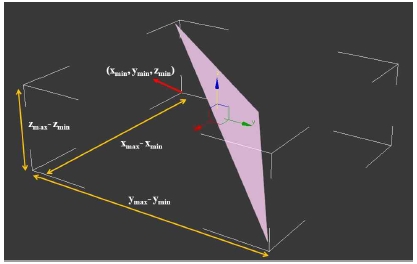
두 번째 방식(그림 4)은 첫 번째 방식에서의 4, 5, 6번째 벡터 요소의 동적 변동폭(dynamic range)을 줄이기 위해 고안되었다. 삼각형의 AABB 최소점 좌표 (xmin, ymin, zmin)와 최대점 좌표 (xmax, ymax, zmax)에 대해 이 형식에서는 AABB의 6차원 벡터를 (xmin, ymin, zmin, xmax – xmin, ymax - ymin, zmax- zmin)으로 표현하며 3차원 질의 점 (x, y, z)는 (x, y, z, x-x, y-y, z-z) = (x, y, z, 0, 0, 0)으로 표현한다.
The second approach to convert a triangle face in 3D space to a 6D vector
다시 말해 두 번째 방식에서는 AABB를 최소점 좌표와 각 축 방향으로의 hypercube의 변의 길이로 표현한다. 이 방식에서는 점의 경우 각 축 방향으로 변의 길이가 0인 hypercube로 볼 수 있다.
3차원 shifted sort 기반 병렬 kANN 기법[4, 5]은 3차원 벡터, 즉, 3차원 공간 상의 점들 사이의 거리만 고려한다. 따라서 질의 점과 가장 가까운 삼각형을 구해야 하는 거리장 계산 등에서는 무한히 많은 점들로 구성되는 삼각형과 같은 점들의 집합과 한 점 사이의 최소 거리 계산에 바로 적용할 수 없다는 한계가 있다. 본 논문에서는 앞서 논의한 대로 3차원 점과 삼각형 face를 6차원으로 확대하고 6차원 벡터 사이의 최소값을 이 논문에서 제안하는 6차원 shifted sort 기반 병렬 kANN 기법에 적용하며 그 기하학적인 의미를 논의하고자 한다.
본 논문에서 구현한 6차원 벡터의 경우, 시각화가 어렵기 때문에 논의를 위해 일반화를 유지하며 2차원 벡터를 4차원 벡터로 확장하는 경우를 고려한다.
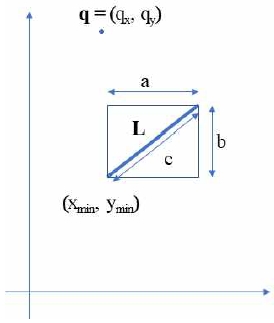
앞서 서술한 두 번째 방식(그림 4)을 적용하여 3차원 공간 상에서 한 점과 삼각형 사이의 거리를 구하는 방법을 2차원 공간 상으로 전환하면 3차원 공간 상의 삼각형은 2차원 공간 상에서 선분으로 표현할 수 있다. 이 상황에서 질의점 q = (qx, qy)와 최소점이 (xmin, ymin)이고 AABB의 각 변의 길이가 각각 a, b인 선분 사이의 거리를 계산하는 상황을 가정한다(그림 5).
distance calculation between the query point q and the segment in 2D space
이 선분과 점 사이의 거리를 계산하는 알고리즘은 이미 최적화된 알고리즘[16]이 연구되어 있으나 본 논문에서는 4차원 벡터로 확장했을 때 Euclidean 거리의 의미를 논의하고자 한다.
그림 4에서 설명한 방식대로 2차원 벡터를 4차원으로 확장시키면 점 q4=(qx, qy, 0, 0), 선분 L은 (xmax, ymax, a, b)로 표현 가능하다. 이 두 4차원 벡터 사이의 Euclidean 거리 D2(q4, L)은 다음과 같이 계산된다.
| (3) |
식 (3)에서 s는 2차원 공간에서 질의점 (qx, qy)와 선분 L의 AABB의 최소점 (xmin, ymin) 사이의 Euclidean 거리에 해당된다. 또한 c는 선분 L의 AABB의 대각선 길이에 해당된다. 따라서 이 4차원 벡터 사이의 Euclidean 거리는 질의 점과 AABB 구간을 차지하는 선분 L 사이의 최소 거리와는 무관하며 ‘최소점에서 질의점으로 향하는 벡터’와 AABB의 대각선 방향 벡터가 서로 직교하는 특수한 상황(그림 6)에서 식 (3)으로 계산되는 4차원 벡터 사이의 Euclidean 거리는 질의점 q’과 AABB의 최대점 사이의 거리가 된다는 사실을 확인할 수 있다.
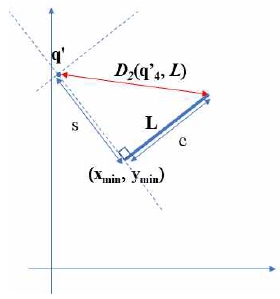
a special case where “the vector from the query point q’ to the minimum point of the AABB” and “the vector along the diagonal direction of the AABB” are orthogonal
따라서 식 (3)으로 계산하는 4차원 벡터 사이의 거리는 질의점과 선분 사이의 거리와는 다르다. 그러나 식 (3)을 Talyor 시리즈로 전개하면,
| (4) |
이 때 s가 선분 L의 길이인 c에 비해 충분히 크다면(즉, s >> c, 다시 말해 질의점 q가 선분 L에서 멀리 떨어져 있는 경우),
| (5) |
즉, 질의점과 선분이 충분히 멀리 떨어져 있는 경우에는 D2(q4, L)를 질의점과 선분의 대략적인 거리의 근사값으로 사용 가능함을 알 수 있다. 이와 마찬가지로 6차원 벡터의 경우에도 삼각형의 넓이에 비해 삼각형과 질의점 사이의 거리가 충분히 클 경우 6차원 벡터의 Euclidean 거리를 3차원 공간 상에서의 삼각형과 질의점 사이의 거리 근사값으로 사용할 수 있으리라 유추한다.
2-3 6차원 병렬 shifted sort 기반 kANN 루틴 구현 테스트
지금까지 논의한 병렬 알고리즘을 NVIDIA CUDA 10.0에서 구현하였다. 실행 환경은 Intel i7-8700 CPU (3.70GHz), RAM 32GB, 64비트 Windows 운영체제, GeForce RTX 2080 Ti (멀티프로세서 68개, GPU 메모리 11GB)으로 구성되었다.
테스트용으로 사용된 mesh는 horse 모델로 꼭지점 19851개, 삼각형 39698개가 적용되었다(그림 7).
Test mesh. Number of vertices = 19851, number of triangles = 39698
테스트는 3차원 데이터의 shifted sort 기반 kANN[4]과 본 논문에서 제안하는 6차원 데이터에 대한 shifted sort 기반 kANN을 비교하였으며 3차원 벡터와 6차원 벡터 각각을 CPU에서 최적화된 성능과 비교하기 위해 ANN[17]과 결과를 비교하였다. 단, 3차원 벡터 비교의 경우 데이터 벡터로 삼각형 mesh의 꼭지점 좌표를 이용하고 6차원 벡터의 경우 삼각형 mesh의 삼각형을 둘러 싸는 AABB로 6차원 벡터를 데이터 벡터로 이용했기 때문에 데이터 벡터의 개수가 서로 다르다(3차원의 경우 19851개, 6차원의 경우 39698개). 그러나 두 차원 모두 비슷한 order를 가지며 상대적으로 질의 벡터의 개수가 최대 223 = 8388608개에 달하기 때문에 성능 추세 비교라는 측면에서 데이터 벡터 개수 차이가 큰 의미를 가지지 않는다고 볼 수 있다.
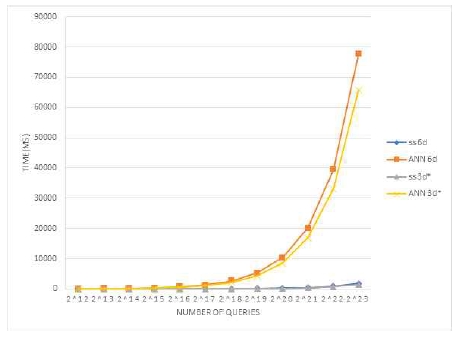
표 4에서는 6차원과 3차원에 대해 제안하는 방식(shifted sort 6D)와 3차원 shifted sort (shifted sort 3D), ANN 6D, ANN3D의 결과를 정리하였다. 그림에서 기존 연구[4]에서 제시한 대로 CPU 기반의 ANN과 제안하는 방법은 큰 성능 차이를 보이고 있다. 그러나 3차원 벡터와 6차원 벡터 사이의 차이는 동일한 방식(GPU 또는 CPU)에서 상대적으로 큰 차이를 보이지 않음을 확인할 수 있다.
Performance comparison between 3D and 6D vectors for ANN and warp-based shifted sort (blocksize = 512, k=8)
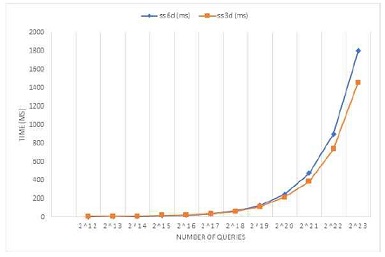
표 5는 GPU 기반 shifted sort에서의 벡터 차원에 따른 처리 시간 변화를 비교한다. 질의 벡터 개수가 상대적으로 적을 경우, 데이터 벡터의 차이 등으로 인해 오히려 3차원 벡터에서보다 6차원 벡터의 처리 속도가 빠른 것을 확인할 수 있으나 질의 벡터 개수가 증가함에 따라 3차원 벡터의 경우가 좀 더 빠르게 실행됨을 확인할 수 있다. 그러나 그 차이는 상대적으로 미미함을 확인할 수 있다. 단 한가지 사례로 일반화하기에는 부족한 측면이 있으나 struct 구조로 벡터 길이를 확장한 6차원 벡터에서 성능이 크게 저하되지 않음을 고려한다면, 보다 일반적인 벡터(d > 6)로의 확장에서도 큰 성능 저하가 일어나지 않을 수도 있다고 가정할 수 있다.
Performance comparison between 3D and 6D vectors for warp-based shifted sort (blocksize = 512, k=8)
Ⅲ. 결 론
3-1 결과 논의
본 논문에서는 GPU에서 shifted sort 기반으로 3차원 데이터를 위해 구현된 kANN 알고리즘을 6차원으로 확장하는 방안을 제안하고 그 기하학적인 의미를 논의하였다. 일반적으로 차원이 증가할 경우, 처리 속도 증가폭이 상당히 큰 것이 일반적이나 표5의 결과를 토대로 볼 때 shifted sort 기반 kANN에서는 차원 증가로 인한 처리 성능의 저하가 그렇게 크지 않음을 실험적으로 확인하였다.
3-2 향후 연구 방향
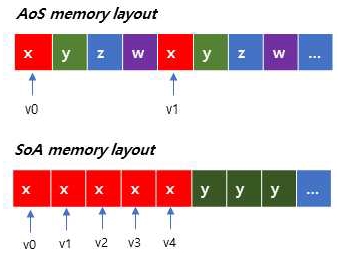
현재 6차원 Morton 코드를 구현하기 위해 struct형의 uint4를 사용하고 이 struct를 배열 형식으로 구성하였기 때문에(표 1) 데이터 구조 측면에서는 AoS(Array of Structures)에 해당된다(그림 8). 일반적으로 GPU 메모리 대역폭 측면에서 이러한 AoS 구조보다는 SoA(Structure of Arrays)가 유리한 것으로 알려져 있다[18].
AoS vs. SoA
따라서 향후 d > 6의 일반적인 벡터로 제안하는 방식을 확장하면서 현재의 AoS 구조를 SoA 구조로 전환하고 그 영향을 분석하는 연구를 수행하고자 한다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제임 (No.20161210200610).
이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임 (NRF-2016R1D1A1B03933660).
본 연구는 한국전력공사의 2018년 착수 에너지 거점대학 클러스터 사업에 의해 지원되었음 (과제번호:R18XA01).
참고문헌
- Minkowski distance in Wikipedia. Available: https://en.wikipedia.org/wiki/Minkowski_distance
- A. N. Papadopoulos, and Y. Manolopoulos, Nearest Neighbor Search: A Database Perspective, 2005 ed., Springer, (2004).
-
S. Arya, and D. M. Mount, “Approximate range searching”, in Proceedings of the eleventh annual symposium on Computational geometry (SCG '95), ACM, Vancouver, British Columbia, Canada, p172-181, (1995).
[https://doi.org/10.1145/220279.220298]
- T. Park, “Optimization of Warp-wide CUDA Implementation for Parallel Shifted Sort Algorithm”, The Journal of Digital Contents Society, 18(4), p739-745, July), (2017.
- H. Kim, and T. Park, “Analysis of GPU-based Parallel Shifted Sort Algorithm as an Alternative to General GPU-based Tree Traversal”, The Journal of Digital Contents Society, 18(6), p1151-1156, October), (2017.
- Axis-Aligned Bounding Box in Gamasutra. Avaiable: https://www.gamasutra.com/view/feature/131833/when_two_hearts_collide_.php
-
T. M. Chan, “Approximate Nearest Neighbor Queries Revisited”, in Proceedings of the thirteenth annual symposium on Computational geometry (SCG '97), ACM Nice, France, p352-358, (1997).
[https://doi.org/10.1145/262839.263001]
-
S. Arya, D. M. Mount, N. S. Netanyahu, R. Silverman, and A. Y. Wu, “An optimal algorithm for approximate nearest neighbor searching fixed dimensions”, Journal of the ACM, 45(6), p891-923, November), (1998.
[https://doi.org/10.1145/293347.293348]
- S. Li, L. Simons, J. B. Pakaravoor, F. Abbasinejad, J. D. Owens, and N. Amenta, "kANN on the GPU with shifted sorting", in Proceedings of the Fourth ACM SIGGRAPH / Eurographics conference on High-Performance Graphics (EGH-HPG'12), Switzerland, p39-47, (2012).
-
T. Park, “Analysis of Morton Code Conversion for 32 Bit IEEE 754 Floating Point Variables”, The Journal of Digital Contents Society, 17(3), p165-172, June), (2016.
[https://doi.org/10.9728/dcs.2016.17.3.165]
- CUDA(Compute Unified Device Architecture) official site. Available: https://developer.nvidia.com/cuda-zone
- Quadtree in Wikipedia. Available: https://en.wikipedia.org/wiki/Quadtree
- Octree in Wikipedia. Available: https://en.wikipedia.org/wiki/Octree
- T. Karrass, Thinking Parallel, Part III: Tree Construction on the GPU, Available: https://devblogs.nvidia.com/parallelforall/thinking-parallel-part-iii-tree-construction-gpu/.
- EEE 754 standard in Wikipedia. Available: https://en.wikipedia.org/wiki/IEEE_floating_point
-
C. Ericson, Real-Time Collision Detection, 1st ed., CRC Press, (2004).
[https://doi.org/10.1201/b14581]
- ANN: A Library for Approximate Nearest Neighbor Searching website. Available: https://www.cs.umd.edu/~mount/ANN/
- J. Cheng, M. Grossman, and T. McKercher, Professional CUDA C Programming, 1st ed., Wrox, chapter 4, (2014).
저자소개
1997년 : 서울대 전기공학부 (공학사)
1999년 : 서울대 전기공학부 대학원 (공학 석사, 반도체 물리 전공)
2006년 : 서울대 전기컴퓨터공학부 대학원 (공학박사, 컴퓨터 그래픽스 전공)
2006년~2013년 : 고려대학교 연구교수
2013년~2017년 : 덕성여자대학교 정보미디어대학 디지털미디어학과 조교수
2018년~현재 : 덕성여자대학교 공과대학 IT미디어공학과 부교수
※관심분야： 컴퓨터그래픽스, 병렬처리, 인공지능, 수치해석, 3차원 모델링
