합성곱 신경망 기반의 PPG 신호 동잡음 구간 검출

Ⅰ. 서 론

정보사회의 네트워크 기술의 획기적인 발전으로 디지털 컨버전스와 유비쿼터스 환경이 구축되면서 이른바 u-Life 시대가 도래하고 있다. 이미 세계 유수의 기관들은 미래의 유망 전략 연구 분야로 컴퓨터 건강 관리 (Computerized Health Care)를 지속적으로 선정하고 있다.

새로운 의료서비스의 패러다임으로 u-헬스 시대가 도래하고 있다. u-헬스는 인간의 평균 수명이 점점 길어지면서 인구의 노령화와 이에 따른 만성질환자가 증가되어, 평소 생활하는 가운데 건강과 질병 관리에 대한 필요성이 증대되면서 새로운 연구 분야와 유망 서비스산업으로 등장하게 되었다. u-헬스의 서비스영역은 크게 의료기관 내, 의료기관과 의료기관 사이, 의료기관과 개인 사이에서 건강 관리 관련 정보 및 서비스를 제공하는 영역으로 나누어진다. 국내의 현황에 비춰볼 때 기관과 개인 사이의 서비스는 원격진료의 법적 문제로 인하여 제한점이 많은 상황이며, 기관과 기관 사이의 서비스 전달 및 공유는 개인 정보 보호로 인하여 활용이 어려운 실정이다. 상용화의 측면에서 선택과 집중을 할 수 있는 분야는 대형병원의 의료기관 내 u-헬스 서비스가 되겠으며, 이를 위한 시스템 구축 기술은 활발하게 연구되고 있다.

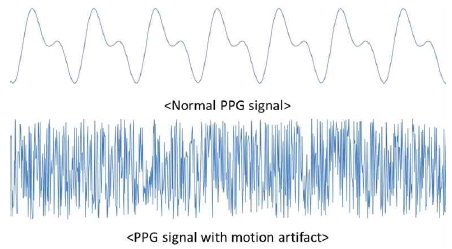
u-헬스 서비스들 중에서 가장 주된 것이 생체신호의 측정 및 모니터링 기술이다. 개개인의 건강 관련 정보를 정확히 측정하는 것은 u-헬스 서비스의 가장 기본적인 필요조건이면서 가장 민감한 영역이기도 하다. 생체신호 데이터에 대한 사용자의 민감도는 매우 크지만, 생체신호 데이터의 획득은 사용자의 상태와 주변 환경에 많은 영향을 받기 때문에 데이터에 대한 정확성, 신뢰도가 중요해진다. u-헬스 서비스를 위해 사용하는 대표적인 생체신호는 심전계 (ECG, Electrocardiograph), 뇌파계 (EEG, Electroencephalograph), 근전계 (EMG, Electromyograph), 광맥파계 (PPG, Photoplethysmograph) 등이 있다. 또한, 생체신호는 각종 디지털 콘텐츠의 휴먼팩터 평가 도구로 활용될 수 있다. 휴먼팩터는 콘텐츠 시청 시 발생하는 시각피로나 신체적 불편감을 유발하는 요인들과 인간의 공간 지각 사이의 함수관계를 규명하여 인간이 다양한 시스템과 안전하게 상호작용 할 수 있는 최적의 환경을 조성하는 것을 목적으로 한다. 휴먼팩터에서 생체신호는 시청자가 느끼는 피로감이나 불편감을 객관적으로 평가하기 위한 지표로 사용될 수 있다. 다양한 생체신호들 중에서 실시간으로 모니터링하기에 간편한 신호는 PPG이다. PPG는 ECG와 유사한 신호로, 빛을 투과하여 혈류량의 흐름을 감지함으로써 심박 및 산소포화도 측정에 사용된다[1]. PPG 신호는 측정에 사용되는 기기가 저렴하며, 다른 기기에 비해 사용자의 움직임이 자유롭다는 장점이 있지만, 움직임으로 인한 신호의 왜곡이 발생하기 쉽다는 단점도 있다[2]. PPG 신호는 0.5Hz에서 5Hz까지의 주파수 대역에서 활성화 되는데, 이러한 활성 주파수 대역 이외에서 발생하는 잡음의 경우 저역 통과 필터와 같은 방법으로 잡음을 제거할 수 있다[3]-[5]. PPG 신호에서 발생할 수 있는 잡음은 전기신호의 잡음에 의해 발생하는 잡음, 생체 전위에 의한 잡음, 사용자의 움직임에 의한 잡음 등으로 다양한 주파수 대역을 갖는다. 잡음의 주파수는 0Hz부터 60Hz, 혹은 그 이상의 대역에서도 발생할 수 있다. PPG 신호에 비해 상대적으로 고주파대역의 잡음들은 미러필터, 평균 이동 필터, 단순 대역 필터 등을 이용하여 제거할 수 있다. 하지만 사용자의 움직임으로 인한 동잡음은 고주파에서뿐 아니라 모든 주파수 대역에서 발생할 수 있는데, 여러 대역의 동잡음 중 고주파 대역에서 발생하는 잡음은 제거할 수 있지만 생체 신호와 비슷한 주파수 대역에서도 잡음이 발생하기 때문에 필터를 이용한 방법으로는 제거하기 어렵다. PPG 신호의 동잡음을 제거하기 위한 많은 노력들이 시도되어왔는데, 적응형 필터를 사용하거나[6]-[8], 시간-주파수 분석을 이용하거나[9]-[10], 블라인드 신호 분리 방법[11] 등이 이용되었다. 하지만 동잡음에 심하게 오염된 PPG 신호는 파형 형태에 심한 변화를 초래하고 이는 신호의 품질을 저하시키기 때문에 추가적인 분석이 필요하다. 뿐만 아니라 병원에서 사용 중인 다양한 생체신호 모니터링 어플리케이션의 경우, 동잡음을 제거하는 대신 동잡음에 오염된 신호구간을 검출하여 분석에서 제외하는 방법을 사용하고 있다. 따라서 PPG 신호에서 동잡음이 포함된 구간을 검출하여 일반적인 잡음제거 방법을 적용할 수 있는 신호와 불가능한 신호를 구분할 수 있는 기술이 적용되어야 한다.

동잡음 구간 검출에는 형태학적 분석이나 고차 통계 분석 기법을 활용한 방법 등이 제안되었다. Sukor등[12]은 PPG 신호의 형태학적 특성 분석에 기반을 둔 알고리즘을 제안하여 약 83%의 정확도로 동잡음 구간을 검출하였다. Selvaraj등[13]은 첨도와 섀넌 엔트로피를 활용한 통계적 접근을 통해 PPG 신호의 동잡음 구간을 추출하였으며 약 88.8%의 정확도를 보였다. Couceiro등[14]은 시간 영역과 주파수 영역에서 특징점을 추출하기 위한 NMIFS 알고리즘[15]과 서포트 벡터 머신 (SVM)을 이용하여 기계학습 기반의 방법을 이용하여 동잡음 구간을 검출하였으며 약 88.5%의 정확도를 보였다. 앞서 서술한 대부분의 연구들이 나쁘지 않은 정확도를 보이는 것은 사실이나 딥러닝을 활용한다면 기존의 방법보다 정확도를 더 높일 수 있을 것이라 생각한다.

딥러닝은 깊은 신경망 (DNN: Deep Neural Network) 알고리즘과 이를 학습하는 방법을 의미한다[16]. 깊은 신경망은 입력층과 출력층을 제외한 은닉층이 2개 이상인 구조의 신경망으로 1980년대에 제안되었으나 학습에 오랜 시간이 걸리고 학습 데이터가 과적합 (overfitting)되는 단점 때문에 일반적인 문제에 사용할 수 없었다. 이러한 문제들은 2000년대 이후 병렬연산이 가능한 GPU (Graphics Processing Unit)의 대거 등장과 과적합을 방지할 수 있는 기법이 제안되며 해결되었다. 이후 딥러닝은 급속도로 발전하였고 현재는 음성인식, 장면인식, 영상복원 등의 다양한 분야에서 딥러닝이 사용되고 있다[17]-[19].

여러 깊은 신경망 중 합성곱 신경망 (CNN, Convolutional Neural Network)은 객체 분류, 탐지, 영역 판독 등 다양한 컴퓨터 비전 분야에 활용되는 깊은 신경망의 구조이다[20]. 층 사이의 노드쌍들 중 일부만 연결하는 합성곱 층 (Convolution layer)과 풀링층 (Pooling layer)이 전체 신경망의 앞쪽에 위치하며 층 사이의 노드를 모두 연결하는 완전연결 층 (Fully connected layer)이 신경망의 뒤쪽에 위치한다. 신경망을 학습할 때는 출력층 뒤에 손실층 (Loss layer)이 추가로 위치하여 신경망의 파라미터들을 학습시킨다. 합성곱 신경망의 주목할 점은 입력층으로 특징 벡터가 아닌 분류할 데이터가 그대로 입력된다는 점이다. 입력된 데이터는 합성곱 층을 통과하며 특징이 추출되고 완전 연결층을 통해 분류된다. 즉 입력 신호의 형상을 직접 모델링 하지 않아도 합성곱 신경망이 알아서 특징 추출과 분류 역할을 모두 수행하는 것이다[21]. 일반적으로 합성곱 신경망은 고정된 크기의 입력 데이터를 사용한다. 합성곱 신경망의 후반부에 위치한 완전연결 층이 고정된 크기의 입력을 받기 때문이다. 반면 합성곱 층은 입력 데이터의 크기에 따라 출력 데이터의 크기가 결정된다. 때문에 완전연결 층을 마스크 크기가 1인 합성곱 층으로 대체하면 입력 데이터의 크기 제한에서 자유로워진 신경망을 학습할 수 있다. 이러한 구조의 신경망은 학습에 사용한 데이터보다 큰 데이터를 입력하면 데이터를 전역 탐색한 결과와 정확하게 동일한 결과를 출력한다.

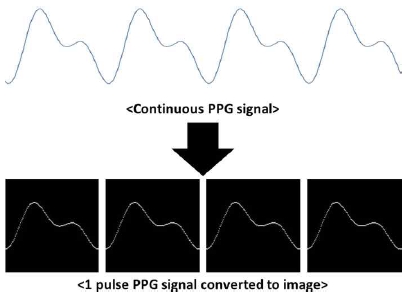
본 연구에서는 합성곱 신경망을 이용하여 PPG 신호의 동잡음 구간을 검출하고자 한다. 연속적으로 획득되는 PPG 신호를 여러 개의 1맥박 구간으로 분리하여 이미지로 변환한 후, 이를 합성곱 신경망을 이용하여 동잡음이 존재하는 구간인지 아닌지 판별하게 된다.

Fig. 1.

Normal and noisy PPG signals

Ⅱ. 연구배경

PPG 신호는 Pulse oximeter를 이용하여 획득되는 신호로, Beer-Lambert 법칙에 따라 광을 인체 특정 부위에 조사하여 조직에 흡수되거나 반사되는 광의 흡수율을 이용하여 혈류를 측정한다. 입사된 빛은 정맥혈과 뼈 조직들을 지나 DC 성분을 생성하며, 동맥혈을 지나는 빛은 AC 성분을 생성하는데, DC 성분은 제거 후 AC 성분만 사용하게 된다. PPG는 측정자의 움직임에 영향을 많이 받으며 호흡에도 영향을 받아 사람마다 신호의 형태가 조금씩 다르며, 특정 질병이 있는 환자의 경우에도 비정상적인 형태의 PPG 신호가 검출될 수 있다. 인간의 일반적인 심박수는 대략 30-300bpm으로, PPG 신호의 주파수는 대략 0.5-5Hz로 제한된다. PPG 신호의 주파수 성분은 호흡 등에 의한 저주파와 심박수에 의한 기본 주파수, 그리고 제2고조파와 제3고조파로 이루어져 있으며, PPG 신호에 동잡음이 유입될 경우, 기본 주파수 부분과 제2고조파, 제3고조파 부분의 주파수 성분이 확연히 구분된다. 움직임에 의한 동잡음은 PPG 신호와 주파수 대역이 겹치고, PPG 신호보다 큰 진폭을 갖는다.

Ⅲ. PPG 신호 동잡음 구간 검출

센서를 통해 획득되는 PPG 신호의 경우, 대략 0.5Hz에서 5Hz까지의 주파수 대역에서 활성화되므로, 해당 주파수 대역 이외에서 발생하는 잡음을 제거할 필요가 있다. 고주파 노이즈와 직류성 노이즈의 경우 대역통과 필터를 이용하여 제거하며, 사용자의 호흡으로 발생하는 기저선을 Q-차 이동 평균 필터와의 차로 제거한다[22]. 기저선이 제거된 PPG 신호 P(n)은 식 (1)과 같이 나타낼 수 있다. 여기서 LBPF(n)은 대역통과필터로 고주파 잡음과 직류성 잡음이 제거된 PPG 신호이다.

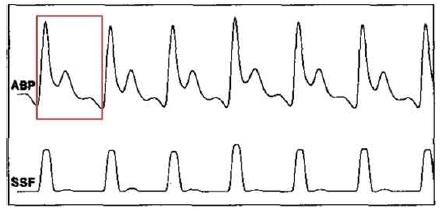
기저선을 제거 후에는 연속적인 PPG 신호를 1맥박 단위의 신호로 분리해야 한다. 이를 위해 Slope Sum Function (SSF)을 적용하여 각각의 맥박을 분리한다. SSF의 목적은 PPG의 맥박 신호에서의 upslope 성분을 강화하고 나머지의 성분은 억제하는 것이다. 시간 i에서 SSF가 적용된 신호 zi는 다음과 같다[23].

여기서 Δyk = yk － yk-1이며, yk는 필터를 통해 잡음이 제거된 PPG 신호이며 w는 윈도우 사이즈이다. SSF 결과를 최대화하기 위해서는 윈도우 사이즈 w를 통상적인 PPG의 맥박 신호에서의 upslope 시간과 비슷하게 설정한다. 이는 125Hz로 샘플링된 신호에서 약 128 ms (또는 16 샘플) 정도이다. PPG의 맥박 신호와 SSF 결과신호 사이의 관계는 그림2와 같다. SSF 결과신호를 획득한 후에는 각 맥박이 시작하는 지점을 찾아 신호를 분리하면 된다. 마지막으로, 그림3과 같이 분리된 맥박신호를 이미지로 변환한다.

Fig. 2.

Relationship between pulse signals in PPG and SSF signals[23]

Fig. 3.

Images of PPG pulse signal

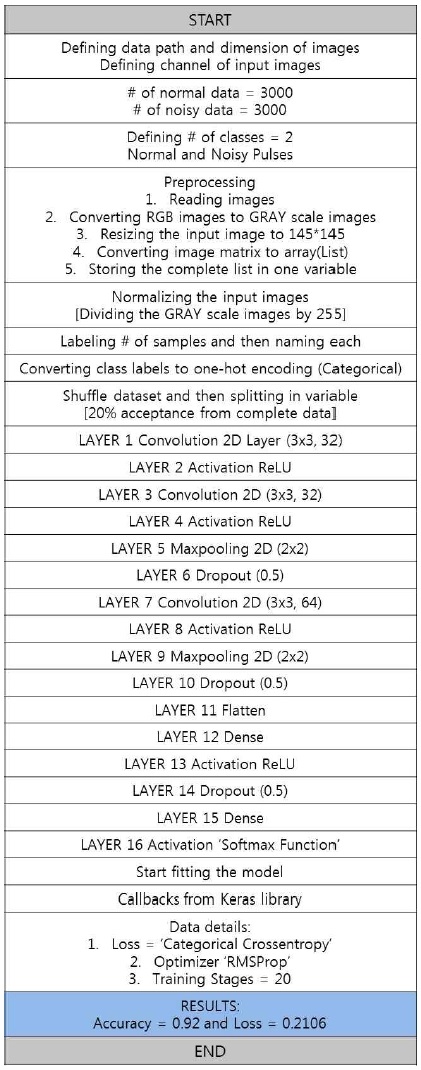
그림4는 합성곱 신경망을 이용한 PPG 신호의 동잡음 구간 검출 과정을 나타낸 순서도이다. 학습에 사용된 데이터는 PhysioNet에서 제공하는 생체신호 데이터베이스를 사용하였다[24]-[26]. 3000개의 정상 신호와 3000개의 동잡음이 포함된 신호를 사용하였으며, 입력 데이터를 랜덤하게 섞은 뒤 80%를 학습데이터로 사용하고 20%를 검증데이터로 사용하였다. 신경망 학습 시 손실함수로 범주형 교차 엔트로피 오차 함수를 사용하였으며, 가중치 업데이트를 위한 최적화 기법으로는 RMSProp[27]를 사용하였다. 이는 학습률을 감소시키는 방법인 AdaGrad[28]를 개선한 방법으로, AdaGrad는 과거의 기울기 값을 제곱해서 계속 더하는 식으로 학습률을 낮추는데, 학습이 진행될수록 제곱의 값으로 학습의 정도가 떨어진다. 하지만 학습이 계속되면서 학습률이 0에 가까워져 학습이 진행이 안 되는 문제가 발생한다. RMSProp은 과거의 모든 기울기를 균일하게 더하지 않고 새로운 기울기의 정보만 반영하도록 해서 학습률이 0에 가까워지는 것을 방지하였다. 또한, 드롭아웃을 설정하여 50%의 비율로 유닛을 제거함으로써 과적합 문제를 방지하였다.

Fig. 4.

Flowchart of motion artifact detection in PPG based on CNN

Ⅳ. 실험 및 결과 분석

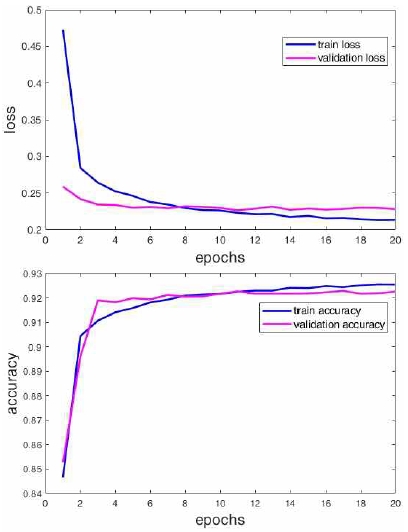
그림 5는 제안된 방법으로 총 20회의 에포크 동안 학습한 결과를 나타낸다. 학습이 진행됨에 따라 손실은 감소하고 정확도는 증가하고 있다. 손실 곡선의 경우 에포크가 증가함에 따라 학습 손실과 검증 손실이 유사한 경향을 보이며, 정확도 곡선의 경우도 마찬가지로 에포크 증가에 따른 학습 정확도와 검증 정확도의 경향이 유사한 것을 확인할 수 있다. 이를 통해 학습된 모델에서 과적합 혹은 과소적합 문제가 발생하지 않는다는 것을 알 수 있다. 제안된 방법은 최종적으로 약 92%의 정확도와 0.21의 손실을 보였으며, Couceiro등[14]과 Selvaraj등[13]이 제안한 방법의 정확도에 비해 약 4%, 그리고 Sukor등[12]이 제안한 방법의 정확도에 비해 약 9% 정도의 향상이 있음을 확인하였다.

Fig. 5.

Training results obtained from the proposed method. (upper)loss curve, (bottom)accuracy curve

Ⅴ. 결 론

본 연구에서는 합성곱 신경망을 이용하여 PPG 신호의 동잡음 구간을 검출하는데 성공하였다. 연속된 신호를 각각의 1맥박 신호로 분리하고 이미지로 변환한 후, 합성곱 신경망을 이용하여 학습하였다. 학습에는 3,000개의 정상신호와 3,000개의 동잡음이 포함된 신호가 사용되었으며, 최종 학습 결과 약 92%의 정확도와 0.21의 손실을 보였다. 결과적으로, 딥러닝을 활용함으로써 기존 방법보다 4 ~ 9% 가량 정확도를 향상할 수 있었다. 본 연구에서 사용된 합성곱 신경망은 PPG 뿐만 아니라 ECG, EEG 등 다양한 생체신호에도 적용이 가능한 기술로서, 유비쿼터스 맞춤형 헬스케어의 핵심 요소기술 중 하나인 생체 신호 처리 분야에서 활용될 수 있다. 이를 통해 환자 모니터링, 원격 진료, 피트니스 등 다양한 헬스케어 분야에 활용이 가능할 것으로 기대된다.

Acknowledgments

본 연구는 2018년도 서경대학교 교내연구비 지원 과제로 수행됨.

참고문헌

• J. Y. Cha, H. S. Choi, J. Y. Shin, and K. J. Lee, “Unconstrained detection of Heart Rate and Respiration using PPG sensor”, in Proceedings of the KIEE Conference, p482-483, Oct.), (2008.
• J. Allen, “Photoplethysmography and its application in clinical physiological measurement”, Physiological Measurement, 28(3), p1-39, February), (2007. [https://doi.org/10.1088/0967-3334/28/3/R01]
• D. Oh, B. Min, S. Kwon, and H. Kim, “Effective PPG signal processing method for detecting emotional stimulus”, Journal of Korea Information Communication Society, 37(5), p393-402, May.), (2012. [https://doi.org/10.7840/kics.2012.37c.5.393]
• J. W. Lim, and E. K. Kim, “Noise reduction by filter improvement in mixed noise image”, Journal of the Institute of Electronics and Information Engineers, 50(5), p231-241, May), (2013. [https://doi.org/10.5573/ieek.2013.50.5.231]
• J. Lee, Y. J. Woo, Y. J. Jeon, Y. J. Lee, and J. Y. Kim, “Moving artefacts detection system for a pulse diagnosis system”, Journal of the Institute of Electronics Engineers of Korea SC, 45(5), p21-27, Sep.), (2008.
• J. Foo, and S. Wilson, “A computational system to optimise noise rejection in photoplethysmography signals during motion or poor perfusion states”, Medical and Biological Engineering and Computing, 44, p140-145, (2006). [https://doi.org/10.1007/s11517-005-0008-y]
• J. M. Graybeal, and M. T. Petterson, “Adaptive filtering and alternative calculations revolutionizes pulse oximetry sensitivity and specificity during motion and low perfusion”, in Engineering in Medicine and Biology Society, 2004. IEMBS '04. 26th Annual International Conference of the IEEE, p5363-5366, (2004). [https://doi.org/10.1109/iembs.2004.1404497]
• S. Kunchon, T. Desudchit, and C. Chinrungrueng, “Comparative evaluation of adaptive filters in motion artifact cancellation for pulse oximetry”, in Signal Processing & Its Applications, 2009. CSPA 2009. 5th International Colloquium on, p307-311, (2009). [https://doi.org/10.1109/cspa.2009.5069240]
• K. A. Reddy, B. George, and V. J. Kumar, “Motion artifact reduction and data compression of photoplethysmo-graphic signals utilizing cycle by cycle fourier series analysis”, in Instrumentation and Measurement Technology Conference Proceedings, p176-179, (2008). [https://doi.org/10.1109/IMTC.2008.4547026]
• Y. S. Yan, C. C. Poon, and Y. T. Zhang, “Reduction of motion artifact in pulse oximetry by smoothed pseudo Wigner-Ville distribution”, Journal of NeuroEngineering and Rehabilitation, 2(1), p3, (2005). [https://doi.org/10.1186/1743-0003-2-3]
• B. S. Kim, and S. K. Yoo, “Motion artifact reduction in photoplethysmography using independent component analysis”, Biomedical Engineering, IEEE Transactions on, 53, p566-568, (2006). [https://doi.org/10.1109/tbme.2005.869784]
• J. A. Sukor, S. J. Redmond, and N. H. Lovell, “Signal quality measures for pulse oximetry through waveform morphology analysis”, Physiological measurement, 32(3), p369, (2011). [https://doi.org/10.1088/0967-3334/32/3/008]
• N. Selvaraj, Y. Mendelson, K. H. Shelley, D. G. Silverman, and K. H. Chon, “Statistical approach for the detection of motion/noise artifacts in Photoplethysmogram”, in Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE, p4972-4975, (2011). [https://doi.org/10.1109/iembs.2011.6091232]
• R. Couceiro, P. Carvalho, R. P. Paiva, J. Henriques, and J. Muehlsteff, “Detection of motion artifact patterns in photoplethysmographic signals based on time and period domain analysis”, Physiological measurement, 35(12), p2369, (2014). [https://doi.org/10.1088/0967-3334/35/12/2369]
• P. A. Estévez, M. Tesmer, C. A. Perez, and J. M. Zurada, “Normalized mutual information feature selection”, IEEE Transactions on Neural Networks, 20(2), p189-201, (2009). [https://doi.org/10.1109/TNN.2008.2005601]
• J. Schmidhuber, “Deep learning in neural networks: An overview”, Neural Networks, 61, p85-117, Jan.), (2015. [https://doi.org/10.1016/j.neunet.2014.09.003]
• P. Y. Simard, D. Steinkraus, J. C. Platt, “Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis”, Proceedings of Seventh International Conference on Document Analysis and Recognition, Edinburgh, UK, Aug), (2003. [https://doi.org/10.1109/ICDAR.2003.1227801]
• A. Graves, A. -R. Mohamed, G. Hinton, “Speech recognition with deep recurrent neural networks”, 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, p6645-6649, May), (2013. [https://doi.org/10.1109/ICASSP.2013.6638947]
• X. -J. Mao, C. Shen, Y. -B. Yang, “Image Restoration Using Very Deep Convolutional Encoder-Decoder Networks with Symmetric Skip Connections”, Proceedings of the 30th International Conference on Neural Information Processing System, p2810-2818, Barcelona, Spain, Dec), (2016.
• Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition”, Proceedings of the IEEE, 86(11), p2278-2324, (1998). [https://doi.org/10.1109/5.726791]
• C. Neubauer, “Evaluation of Convolutional Neural Networks for Visual Recognition”, IEEE Transaction on Neural Networks, 9(4), p685-696, July), (1998. [https://doi.org/10.1109/72.701181]
• B. -R. Lee, and J. -W. Lee, “Design of Motion Artifacts Filter of PPG Signal based on Kalman filter and Adaptive filter”, Journal of the Korea Institute of Information and Communication Engineering, 18(4), p986-991, April), (2014. [https://doi.org/10.6109/jkiice.2014.18.4.986]
• W. Zong, T. Heldt, G. B. Moody, and R. G. Mark, “An open-source algorithm to detect onset of arterial blood pressure pulses”, in Computers in Cardiology, p259-262, (2003). [https://doi.org/10.1109/CIC.2003.1291140]
• A. E. W. Johnson, T. J. Pollard, L. Shen, H. L. Li-wei, M. Feng, M. Ghassemi, B. Moody, P. Szolovits, L. A. Celi, and R. G. Mark, “MIMIC-III, a freely accessible critical care database”, Scientific data, 3, p160035, (2016). [https://doi.org/10.1038/sdata.2016.35]
• T. J. Pollard, and A. E. W. Johnson, The MIMIC-III Clinical Database, (2016).
• A. L. Goldberger, L. A. Amaral, L. Glass, J. M. Hausdorff, P. C. Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C. K. Peng, and H. E. Stanley, “PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals”, Circulation, 101(23), pe215-e220, (2000). [https://doi.org/10.1161/01.CIR.101.23.e215]
• T. Tieleman, and G. Hinton, Lecture 6.5 - RMSProp, COURSERA: Neural Networks for Machine Learning, University of Toronto, Toronto, ON, Technical report, (2012).
• J. Duchi, E. Hazan, and Y. Singer, “Adaptive subgradient methods for online learning and stochastic optimization”, Journal of Machine Learning Research, 12, p2121-2159, July), (2011.