게이미피케이션 개발을 위한 게임 메커닉스와 PLEX 최적 개수

Ⅰ. 서 론

게이미피케이션(Gamification)은 게임을 구성하는 요소를 게임이 아닌 맥락(Non-Game Context)에 적용하여 새로운 가치를 만들어 내는 기법이다[1, 2]. 게이미피케이션을 적용하여 사용자에게 게임적 경험(Gameful Experience)을 제공하고, 업무환경 혁신, 교육환경 혁신 사례가 발표되기 시작했다. Stanculescu et. al.[3]은 업무 환경에 게이미피케이션을 적용했다. 적용 목적은 지원들의 사회성 향상, 업무 관련 전문지식 습득이었다. 206명의 직원을 대상으로 2달간 실험을 진행했으며, 게이미피케이션이 직원들의 고관여 향상, 전문 지식 습득 개선, 사회성 향상에 긍정적인 영향을 미치는 것으로 나타났다. 뿐만 아니라, 게이미피케이션으로 의사소통 및 관계 개선도 가능하다. Kang et. al.[4]는 게이미피케이션이 적용된 앱을 통해 의사소통의 장벽을 낮추고, 친목도모가 가능하며, 관계 개선도 가능함을 증명했다.

이처럼 게이미피케이션은 다양한 분야에서 새로운 가치를 만들어내기 시작했다. 가치 창출과 더불어 더욱 정교하고 효율적인 게이미피케이션을 개발하기 위한 연구도 시작됐다. 체계적인 게이미피케이션 개발 방법론을 통해 실패 가능성을 최소화하고 효율적인 게이미피케이션을 개발하기 위해서다. 현재 발표된 게이미피케이션 개발 방법론으로 4F 프로세스[5], 6D 프로세스[6], 옥탈리시스[7]등이 존재한다. 뿐만 아니라, 기존에 발표된 개발 방법론에 메타 분석(Meta-Analysis)를 적용한 게이미피케이션 디자인 프레임워크[8]도 존재한다.

하지만 대부분의 게이미피케이션 개발 방법론은 일정 수준 이상의 게이미피케이션 지식을 가지고 있거나, 게이미피케이션 개발 전문가만 사용이 가능했다. Park & Kim[5]에 따르면, 대부분의 게이미피케이션 개발 방법론은 절차에 따라 개발 할 경우, 큰 문제없이 게이미피케이션 개발이 가능하나, 게임 메커닉스(Game Mechanics)나 재미 경험 설정 등 일부 절차는 노하우(Know-How)적 요소이기 때문에 게이미피케이션 관련 지식이 없거나 상대적으로 부족한 사람들은 사용하기가 어렵다는 것이었다. 여기서 언급한 노하우적 요소는 게임 메커닉스를 몇 개나 적용할지, 재미 경험은 얼마나 설정을 해야 하는 것이다. 적용 가능한 게임 메커닉스의 종류나 재미 경험의 종류를 제시하지만 어떤 요소를 어떻게 적용해야 하는지에 대해서는 언급한 방법론이 존재하지 않는다[9].

또한, 4차 산업혁명으로 인해 과거에 비해 비교적 머신러닝을 쉽게 개발이 가능한 시대이다. 간단한 라이브러리를 참고하거나, 전용 툴을 사용한다면, 간단한 머신러닝 구현이 가능하다. 본 연구에서도 게이미피케이션 개발에 도움을 주는 머신러닝 개발에 대한 필요성을 인지했다. 과거 개발된 게이미피케이션 사례를 바탕으로 앞으로 게이미피케이션을 개발 할 때, 필요한 요소에 대한 힌트를 얻을 수 있다면 실패 가능성이 최소화된 개발이 가능할 것이다[9].

이러한 문제를 해소하고, 머신러닝 활용의 가능성을 알아보기 위해 마르코프 체인[10]을 활용한 연구를 진행했다.

Ⅱ. 마르코프 체인과 안정상태

마르코프 체인[10]은 특정 사건이 과거에 발생한 확률을 기반으로 미래를 예측하는 모형이다. 특정 사건이 과거에 일어난 관측치 X₀, X₁, ..., X_{n - 1}과 현재의 상황 X_n을 통해 미래의 예측치 X_{n + 1}을 예측한다. 미래의 예측치는 현재 상태 X_n에 의존한다고 가정한다. X_n은 n 시점에서의 확률 과정 상태(state)라고 정의한다. 이러한 상태의 집합을 상태 공간(state space)라고 정의한다. 시공간이 연속적인 형태로 분포하는 사건을 마르코프 과정(Markov Process)에 있다고 하며, 확률 과정의 상태 공간 S와 시간 공간 T는 이산(Discrete)의 형태로 분포할 경우, 마르코프 특성(Markovian Property)이라고 정의된다(1).

마르코프 특성은 미래의 조건부 확률이 과거의 특정 사건과 현재의 상태를 감안할 때, 해당 사건은 과거 사건과 무관하며 현재 상태에 의존한다. 마르코프 체인에 대한 조건부 확률을 전이 확률(Transition Probability)라고 정의한다. 또한 과거 전이 확률로부터 마르코프 특성을 활용해 다음 단계의 조건부 확률을 구할 수 있으며, 이를 n단계 전이확률(n-Step Transition Probability)라고 정의한다. 초기시점 n에서 상태 I에 있다가 n+1 시점의 j로 바뀔 때, 확률은 P_ij로 표현이 가능하다. 이것은 조건부 확률을 의미한다(2).

전이 확률은 n×n의 정방형 행렬로 표현이 가능하며 이를 전이확률행렬(Transition Matrix)라고 정의한다. 전이확률행렬 내의 P_ij는 0과 1사이의 값을 가지고 있으며, 상태 I에서 다음 상태로 전이할 때, 상태 j와 나머지 상태를 합한 확률의 값은 1이 되어야 한다[10].

상태 공간 S = {0, 1, 2, ..., n}를 갖는 마르코프 체인의 1단계 전이확률 P_ij(i, j ∈ S)라고 표시하고, k번째 전이확률을 $$ P_{ij}^{\left(k\right)}\left(i,j\in S\right)$$로 나타낸다. k단계 전이확률 P^k는 k-1단계 전이행렬과 1단계 전이확률의 곱으로 구할 수 있으며 이를 채프만-콜모고로프 방정식(Chapman-Kolmogorov Equation)이라고 한다(3).

채프만-콜모고로프 방정식에서 몇 차례의 전이를 겪으면 초기분포의 영향이 사라지고 안정된 확률분포로 수렴한다. 이를 안정 상태(Steady State)에 있다고 한다[10].

Ⅲ. 연구 방법

게이미피케이션 개발 절차 중에서 게임 메커닉스와 재미경험 설정 개수를 예측하기 위해 사례를 수집하고, 각 사례 별 적용된 게임 메커닉스와 재미 경험을 분석하고, 적용된 개수를 바탕으로 전이확률행렬을 만들었다. 전이확률행렬을 구한 뒤, 마르코프 체인을 적용하여 적용해야 할 게임 메커닉스와 재미 경험의 개수를 예측했다. 게임 메커닉스와 재미 경험은 [5]의 기준을 따랐다. 사례 분석 및 마르코프 체인을 적용하기 위해 R Studio – Markov Chain Package를 사용했다.

3-1 게이미피케이션 사례 수집

게임 메커닉스와 재미경험을 분석하기 위해 사례를 수집했다. 사례는 구글 검색과 ‘엔터프라이즈 게이미피케이션 위키(Enterprise Gamification Wiki)’페이지에 기록된 사례를 포함하여 869개를 수집했다. 기간은 2017년 12월부터 2018년 8월까지 수집했다. 논문에 소개된 사례는 제외했다.

‘좋은 게이미피케이션’에 대한 기준은 명확하지 않다. 본 연구는 일반 대중이 플레이가 가능하며, 콘텐츠가 일정 기간 이상 플레이 가능(했었던)한 게이미피케이션만 수집했다. 대중에게 공개된 사례는 효과검증을 통해 불특정 다수에게 유의미한 효과가 있음을 검증했기 때문에 일반 사례만 수집했다.

게이미피케이션 사례는 본 연구진이 직접 플레이가 가능하거나, 소개 영상이 가능한 사례만 취급했다. 논문 사례는 스크린 샷(Screen Shot) 위주로 설명되어 있어서 분석이 불가능하다. 다음의 표 1은 수집된 사례의 연도분포이다. 연도는 2012년 이전, 2012 ~ 2017년으로 구분했다.

Table 1.

Distribution of Published Year

Table 2.

Applied Game Mechanics Summary

사례 분석은 분석결과의 타당성을 확보하기 위해 개발 방법론을 적용했다. 4F 프로세스[5]에 제시된 게임 메커닉스와 PLEX(PLayful EXperience) 재미 요소[11]을 기반으로 분석했다. PLEX 모델은 기존 상업성 게임을 분석하여 인간이 경험 할 수 있는 재미 유형을 정리한 모델이며, 22가지 재미 경험이다. 게임 메커닉스는 4F 프로세스가 제시한 25가지 중에서 분석이 가능한 18개의 게임 메커닉스로 사례를 분석했다. 분석에 사용된 게임 메커닉스는 표 2와 같다. PLEX 재미 경험[11]은 표 3과 같이 요약된다.

Table 3.

Applied PLEX Fun Factors Summary

수집한 사례의 게임 메커닉스(표 4)와 PLEX 재미 요소(표 5)을 분석하고, 적용된 개수를 정리했다. 사례는 연도 별로 정리했다. 2012년 이전은 B12년으로 표시했다. 게임 메커닉스는 최소 3개부터 최고 18개 까지 적용된 것으로 나타났다. PLEX 재미 유형은 최소 2개, 최고 18개가 적용된 것으로 나타났다.

Table 4.

Applied Number of Game mechanics in each Cases

Table 5.

Applied Number of PLEX Fun Factors in each Cases

3-3 예측 결과 검증

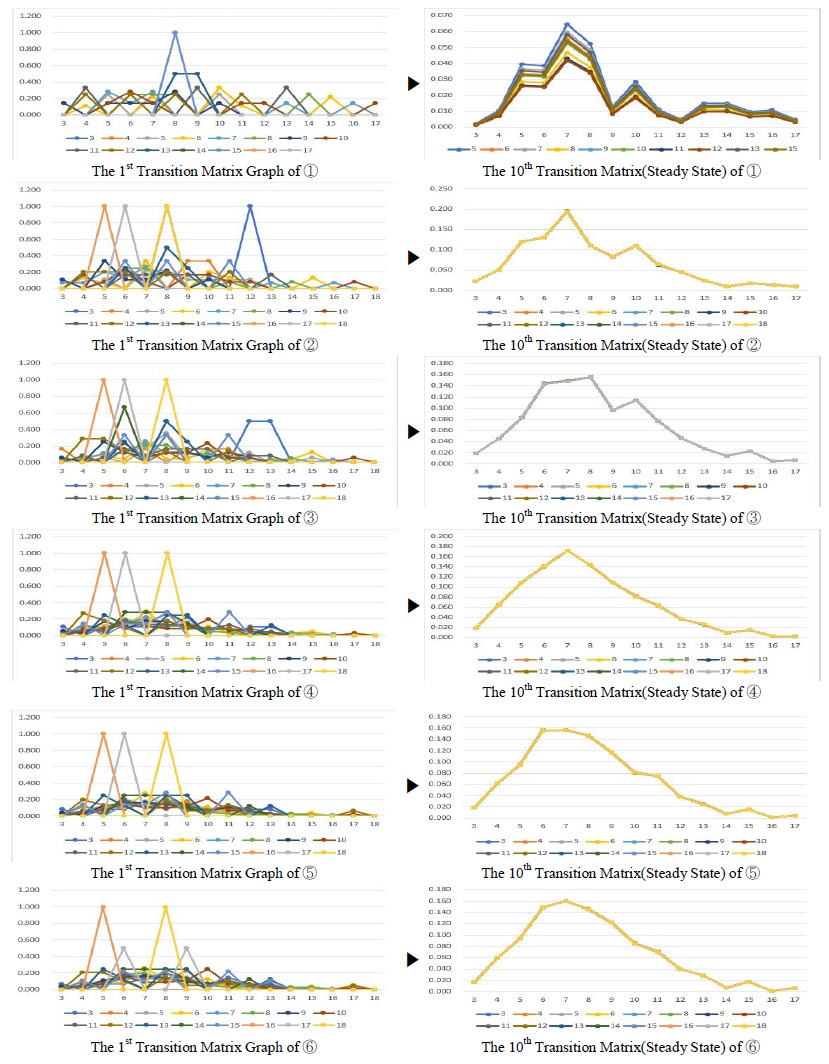
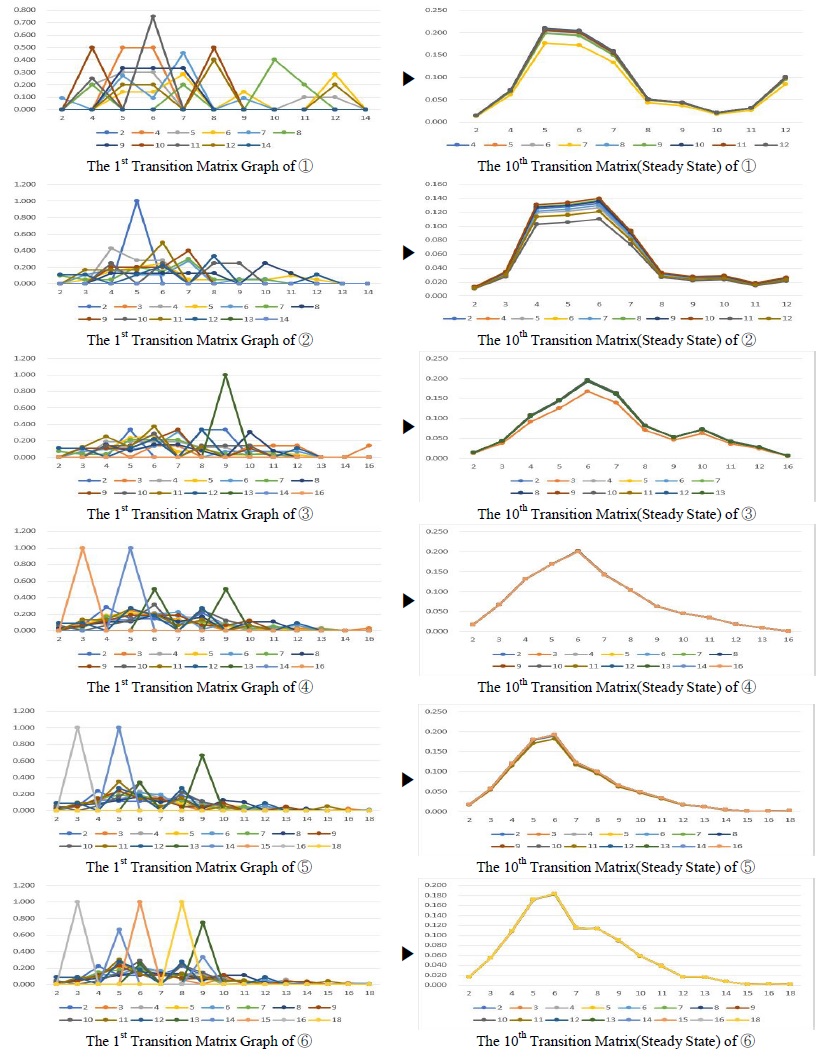
2012이전 사례부터 2016년 사례를 적용하여 2017년 실제 사례를 비교한 결과는 다음의 표 6, 7과 같다. 연도 표시는 분석 방법에서 제시한 1~ 5번으로 표시했다. 표 6은 게임 메커닉스개수의 예측치와 실제 관측치를 비교한 결과이며, 표 7은 PLEX 재미 유형의 예측치와 실제 관측치를 비교한 결과이다. 그림 1과 2는 ① ~ ⑤의 1단계 전이확률행렬과 안정 상태를 그래프로 표현한 것이다.

Table 6.

The Comparison Results of # of Game Mechanics

Table 7.

The Comparison Results of # of PLEX Fun Factors

Fig. 1.

1st Transition Matrix and 10th Transition Matrix(Steady State) for ① ~ ⑥ of # of Game Mechanics

Fig. 2.

1st Transition Matrix and 10th Transition Matrix(Steady State) for ① ~ ⑥ of # of PLEX Fun Factors

분석 결과에 따르면, 5개 예측 결과 모두 통계적으로 유의미했다. 이는 마르코프 체인을 활용한 예측치와 실제 관측치가 같은 방향성을 띄고 있음을 의미한다. 게임 메커닉스 개수의 ① ~ ⑤ 모두 0.8이상의 피어슨 상관계수를 확인했으며, 0.5 이상의 켄달 상관계수를 확인했다. 두 결과 모두 통계적으로 유의미한 결과임을 확인했다(p < 0.01). PLEX 재미 유형 개수의 경우, ① ~ ⑤ 모두 0.4 이상의 피어슨 상관계수를 확인했으며, 0.4이상의 켄달 상관계수를 확인했다. 두 결과 모두 통계적으로 유의미한 결과임을 확인했다.(p < 0.01, p < 0.05).

그림 1과 2에서는 그래프가 가장 높은 곳의 개수가 유의미한 개수임을 나타낸다. 과거 사례의 게임 메커닉스 개수는 5 ~ 8개 사이가 적절한 것으로 나타났다. PLEX 재미 유형은 4 ~ 6개 사이가 적절한 것으로 나타났다.

Ⅳ. 게임 메커닉스와 PLEX 개수 예측 결과

본 연구진이 수집한 사례를 바탕으로 향후 게이미피케이션 개발에 필요한 게임 메커닉스와 PLEX 재미 유형의 예측 개수는 표 8과 같다. N은 게임 메커닉스와 PLEX 재미 유형 개수를 의미하며, Ratio는 2012년 이전 사례 ~ 2017년 사례 분석 결과에 마르코프 체인을 적용한 안정 상태 비율이다. S/R은 채택여부이다. S(Suggestion)는 지지, R(Rejection)은 기각을 의미 한다.게임 메커닉스의 경우 6개 ~ 8개가 가장 적절한 개수로 예측됐다. PLEX 재미 유형의 경우, 5개 ~ 6개가 가장 적절한 개수로 예측됐다.

Table 8.

The Prediction Results of This Study

표 8에 대한 그래프는 그림 1, 2에서 확인 가능하다. 그림 1의 ⑥은 2012년 이전 사례부터 2017년 사례의 게임 메커닉스에 마르코프 체인을 적용한 안정 상태를 그래프로 표현한 것이다. 그래프 상으로도 6 ~ 8이 가장 높은 값을 기록한 것으로 나타났다. 그림 2의 ⑥은 2012년 이전 사례부터 2017년 사례에 PLEX 재미 유형에 마르코프 체인을 적용한 안정 상태를 그래프로 표현한 것이다. 그래프 상으로도 5 ~ 6이 가장 높은 값을 기록한 것으로 나타났다.

Ⅴ. 결 론

본 연구는 게이미피케이션 개발 방법론에 대한 문제점을 해결하기 위한 연구이다. 기존에 발표된 게이미피케이션 개발 방법론은 해당 절차에 따라 게이미피케이션 개발이 가능하다. 하지만, 게임 메커닉스나 플레이어에게 제공하는 재미 경험을 적용하는 것은 노하우적인 요소이다.

이러한 문제점을 해결하기 위해 마르코프 체인을 통해 게임 메커닉스와 재미 요소 개수를 예측하는 연구를 진행했다. 2017년 12월부터 2018년 8월까지 게이미피케이션 사례를 수집했으며, 4F 프로세스[5]에 근거하여 게임 메커닉스를 분석했고, 재미 경험은 PLEX 모델을 적용했다. 총 869개 사례를 수집 및 분석했으며, 마르코프 체인을 적용하여 적절한 게임 메커닉스와 PLEX 재미 유형 개수를 예측했다.

연구결과, 게임 메커닉스는 6개 ~ 8개, PLEX 재미 유형은 5개 ~ 6개가 적절한 것으로 예측됐다.

본 연구결과는 게이미피케이션에 대한 지식이 부족하거나, 게이미피케이션 개발에 어려움을 느끼는 사용자에게 선택의 폭을 제한하여 효율적인 의사결정을 유도하는 것이 목적이다. 힉스의 법칙[14]은 사용자에게 적절한 선택지를 제공하여 의사결정에 소요되는 시간을 최소화한다. 적절한 게임 메커닉스와 PLEX 재미 유형 개수를 제안하여 사용자가 효율적으로 방법론을 사용할 수 있도록 유도해야 한다. 뿐만 아니라, 너무 많은 요소를 적용했을 경우, 해당 게이미피케이션을 사용하는 사용자에게 기능 피로감을 경험한다. 기능 피로감으로 인해 게이미피케이션이 전달하고자 하는 본질을 제대로 전달하지 못할 가능성도 존재한다[154]. 그렇기 때문에 적절한 개수를 제안하여 효율적인 게이미피케이션 개발이 가능하도록 해야 한다.

인공지능을 이용한 방법은 우리가 찾지 못한 것을 알려준다. 본 연구결과를 토대로 게이미피케이션 개발에 도움을 주는 머신러닝을 개발의 필요성을 제언한다. 마르코프 체인은 강화학습(Reinforcement Learning) 알고리즘 중 하나이다. 앞으로는 머신러닝을 활용한 연구가 지속적으로 진행되어야 한다. 본 연구 결과를 바탕으로 게이미피케이션 개발에 도움이 되는 머신러닝을 개발할 때, 유의미한 영향을 미칠 것으로 추측된다. Park et. al.[16]은 비지도 학습 분야 중 하나인 데이터 클러스터링을 활용하여 플레이어 유형을 분류하는 연구를 진행했으며, 바틀의 플레이어 유형[17]이 비교적 우수한 이론임을 증명했다.

본 연구의 한계점 및 향후 연구 방향은 다음과 같다. 본 연구진이 수집한 사례의 분포가 비교적 2013년과 2015년으로 치중되어 있다. 추가 연구를 진행하기 전 연도별 사례를 추가하여 향후 연구를 진행해야 한다. 뿐만 아니라, 본 연구진의 전이확률행렬은 추정치이다. 그렇기 때문에 해당 추정치를 검증 할 수 있는 통계적 기법이 필요하다. 추가 연구에서는 추정치 검증 방법을 적용하여 연구의 타당도, 신뢰도, 일반화 가능성을 확보해야 한다. 게임 메커닉스를 분석하는 것은 기준과 적용방법이 명확하기 때문에 큰 차이가 없다. 하지만 재미 경험의 경우, 사용자마다 받는 느낌이나 경험이 다르다. 재미 경험은 수치적으로 측정이 불가능하기 때문에 분석하기가 모호하다. 해당 한계점을 개선하기 위해 분석 결과를 게이미피케이션 전문가 자문을 통해 분석 결과의 신뢰도를 확보한다면, 본 연구 결과의 신뢰도 개선이 가능할 것이다.

Acknowledgments

본 연구는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구로서, 관계부처에 감사드립니다(No.2017R1A2B2002798).

References

• S. Deterding, et al , "From game design elements to gamefulness: Defining gamification,", in Proceedings of the 15th International Academic MindTrek Conference: Envisioning Future Media Environments, (2011), p9-15.
• I. Bunchball, "Gamification 101: An introduction to game dynamics,", (2012).
• L. C. Stanculescu, et al , "Work and play: An experiment in enterprise gamification,", in Proceedings of the 19th ACM Conference on Computer-Supported Cooperative Work & Social Computing, (2016), p346-358. [https://doi.org/10.1145/2818048.2820061]
• S. Kang, J. Jung, S. Park, S. Kim, "Communication Effects of Gamification App: Focused on <Everybody's Neghbor>", Journal of Digital Contents Society, 19(7), p1245-1251, (2018).
• S. Park, S. Kim, "Gamification Development Methodology – Design and Comparative Analysis of 4F Process,", Journal of Digital Contents Society, 19(6), p1131-1144, (2018).
• K. Werbach, and D. Hunter, The Gamification Toolkit: Dynamics, Mechanics, and Components for the Win, Wharton Digital Press, (2015).
• Y. Chou, Actionable Gamification: Beyond Points, Badges, and Leaderboards. Octalysis Group, (2015).
• A. Mora, et al , "A literature review of gamification design frameworks,", in 2015 7th International Conference on Games and Virtual Worlds for Serious Applications (VS-Games), (2015), p1-8. [https://doi.org/10.1109/vs-games.2015.7295760]
• S. Park, S. Kim, "A Prediction of the Number of Game mechanics and PLEX Fun Factors applying Markov Process", Korea Game Society Spring Academical Conference 2018, (2018).
• F. S. Hillier, Introduction to Operations Research, Tata McGraw-Hill Education, (2012).
• J. Arrasvuori, M. Boberg, and H. Korhonen, "Understanding playfulness-an overview of the revised playful experience (PLEX) framework,", in Proc. of Design & Emotion 2010 Conference, Design and Emotion Society, (2010).
• H. C. Kim, S. K. Choi, and D. H. Choi, "A simulation comparison on the analysing methods of Likert type data,", Journal of the Korean Data and Information Science Society, 27(2), p373-380, (2016). [https://doi.org/10.7465/jkdi.2016.27.2.373]
• G. F. Tondello, et al , "The gamification user types hexad scale,", in Proceedings of the 2016 Annual Symposium on Computer-Human Interaction in Play, (2016), p229-243. [https://doi.org/10.1145/2967934.2968082]
• W. E. Hick, "On the rate of gain of information,", Q. J. Exp. Psychol., 4(1), p11-26, (1952).
• S. Kim, Engineering and Management, Hanbit Academy, (2017).
• S. Park, B. Kang, S. Kim, S. Kim, “An Analysis of Player Types using Data Clustering in Gamification”, Journal of Korea Game Society, 17(6), p77-88, (2017).
• R. Bartle, “Hearts, Clubs, Diamonds, Spades: Players who suit MUDs”, Journal of MUD research, 1(1), (1996).