단일 자연 영상에서 그림자 검출 및 제거를 위한 선형 회귀 기반의 1D 불변 영상

Ⅰ. 서론

그림자(shadow)는 자연 경관에서 관찰되는 일반적인 현상으로 자연 영상(natural scene image)의 구조와 의미를 이해하는데 효과적지만 특징 검출(feature detection), 물체 인식(object recognition) 및 장면 분석(scene analysis)등과 같은 인식을 복잡하게 할 수 있다 [1][2]. 따라서 그림자 검출 및 제거는 디지털 영상 분석 과정에서 필수적으로 고려되어야 한다.

그림자는 장면의 조명에서 가장 두드러진 효과 중의 하나로 주요 특징은 크게 밝기(intensity), 국부블록의 최대치(local max) 및 왜도(skewness) 등과 같은 변형성과 근접화소의 조도불변(illumination-invariant), 기울기(gradient)와 텍스처(texture) 유사도 등과 같은 불변성 특징을 갖는다 [2-4].

본 논문에서는 RGB 칼라 모델 기반의 단일 자연 영상에서 그림자 특징인 1D 불변 영상(1D invariant image, 이하, 불변 영상)을 획득하는 기존의 방법들을 기술하고, 칼라 영상의 각 채널의 밴드 비의 로그(the log of the band-ratios)와 선형 회귀(linear regression)를 통한 불변 영상 획득 방법을 제안한다. 본 논문의 구성은 다음과 같다. 2장에서는 기존의 불변 영상들을 설명하고, 3장에서 선형 회귀 기반의 불변 영상을 획득하는 제안하는 방법을 기술한다. 4장에서는 기존과 제안 방법을 비교 분석하고, 5장에서 결론을 맺는다.

Ⅱ. 기존의 불변 영상들

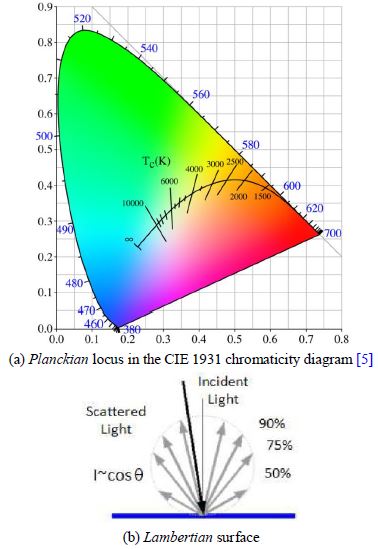
본 장에서는 단일 자연 영상에서 그림자를 검출하고 제거하는 과정에서 특징요소로 적용되는 불변 영상들에 대해 기술한다. 불변 영상은 다양한 선행 연구들에서 Planckian locus와 Lambertian surface 이론을 적용하였으며 [5][6], 선행 연구들은 단일 자연 영상의 각 채널의 밴드 비의 로그를 이용한다는 점에서 공통점을 갖는다.

2-1 디지털 영상의 형성 모델 기반의 불변 영상

선행 연구 [7]에서 디지털 영상은 그림 1의 Planckian locus의 스펙트럼 분포와 3개의 빛 파장에 의해 Lambertian surface에 반사되어 형성되며, 이때 이미지화되는 조도불변 영상은 식 1에 의해 획득할 수 있다. 식 1에서 빛 파장의 센서 응답 R₁, R₂ 및 R₃는 Planckian light에 따라 RGB 칼라 모델의 blue, green 및 red 채널과 상관되며 [7], α는 3채널 카메라의 빛 파장 응답으로 결정된다. 따라서 RGB 칼라 모델 기반의 영상에서 조도불변 영상 ℑ는 식 2에 의해 획득할 수 있다.

$\[ I=log\left(R_2\right)-\alpha log\left(R_1\right)-\left(1-\alpha \right)log\left(R_3\right). \]$

(1)

$\[ \Im =0.5+log\left(G_{ch}\right)-\alpha log\left(B_{ch}\right)-\left(1-\alpha \right)log\left(R_{ch}\right). \]$

(2)

Fig. 1.

Planckian locus and Lambertian surface

2-2 Finlayson의 불변 영상

선행연구 [8]에 의하면 Planckian light가 Lambertian surface에 이미지화된다면 RGB 칼라 영상의 각 채널의 밴드 비의 로그 영상은 점으로 표출되고, 식 3과 식 4에 의해 계산된다.

$\[ \begin{array}{cc}{c}_{ k}=\frac{R_k}{R_p},\hfill & k=1,2.\hfill \end{array} \]$

(3)

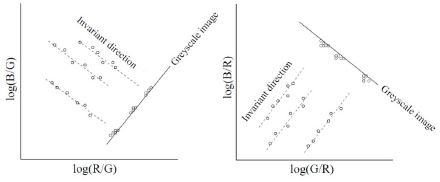
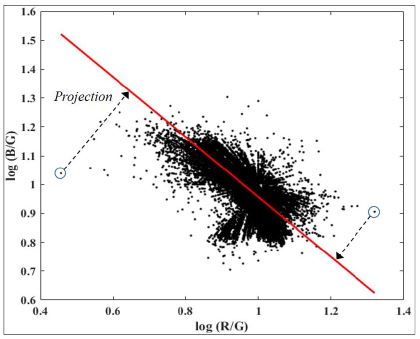
식 3에서 p는 RGB 칼라 영상의 하나의 채널을 나타내며, k는 나머지 두 채널을 의미한다. 식 4는 식 3에 로그를 취한 것으로 그림 2와 같이 그레이스케일(grayscale) 영상으로 투영(projection) 시 최상의 방향을 찾기 위해 적용된다.

$\[ \begin{array}{cc}{\rho }_k\equiv log\left(c_k\right),\hfill & k=1,2.\hfill \end{array} \]$

(4)

Fig. 2.

Acquisition of grayscale image line by projection in the invariant direction [8]

그림 2에서 보여주듯이 직교 방향 e^⊥≡(e_k - e_p) 으로 ρ_k를 투영한 후 지수함수를 취하면 불변 영상을 획득 할 수 있으며 [8], 식 5와 같다. 보정되지 않은 카메라의 경우 투영 방향이 지정되지 않기 때문에 식 5에 의해 구해진 불변 영상 ℑ의 엔트로피(entropy)를 최소화할 수 있는 각도 θ 방향으로 투영하여야 하며, 최종 불변 영상은 식 6에 의해 획득된다.

$\[ \begin{array}{cc}{I}_{\perp }={\rho }_k•e^{\perp },\hfill & \Im =exp\left(I_{\perp }\right).\hfill \end{array} \]$

(5)

$\[ \therefore \Im ={\rho }_{1}cos\left(\theta \right)+{\rho }_{2}sin\left(\theta \right). \]$

(6)

식 6에서의 각도 θ는 ρ₁과 ρ₂ 간의 엔트로피 η_k를 계산한 후 최소값을 취득하며 [9], 투영 각도 θ는 식 7에 의해 구해진다.

$\[ \theta =min\left({\eta }_k\right). \]$

(7)

그림 3은 RGB 칼라 영상을 식 3부터 식 7에 의해 획득한 주요 결과 영상들과 불변 영상을 보이고 있으며, 식 3에서 p는 blue, k = 1,2는 각각 red와 green 채널로 설정하였다.

Fig. 3.

Images obtained by (3) to (7)

2-3 기하 평균 기반의 불변 영상

기하 평균(geometric mean)은 n개의 양수 값을 모두 곱한 것의 n제곱근으로, 집합 {a₁,a₂,...,a_n}의 기하 평균은 식 8과 같이 정의할 수 있다.

$\[ \begin{array}{c}{\left(\prod _{i=1}^n{a}_i\right)}^{1/n}={\left(a_1\times a_2\times \cdots \times a_n\right)}^{1/n}\hfill \\ =\sqrt[n]{a_1\times a_2\times \cdots \times a_n}.\hfill \end{array} \]$

(8)

RGB 칼라 영상에서의 기하 평균은 $$ \sqrt[3]{R\times G\times B}$$를 나타내며, 식 3은 식 9와 같이 재정의 된다.

$\[ \begin{array}{cc}{c}_k=\frac{R_k}{R_p},k=\mathrm{1,2},3,\hfill & p=\sqrt[3]{R\times G\times B}.\hfill \end{array} \]$

(9)

$\[ \begin{array}{cc}{\rho }_k\equiv log\left(c_k\right),\hfill & k=\mathrm{1,2},3.\hfill \end{array} \]$

(10)

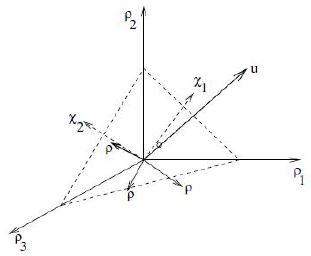
RGB 칼라 영상의 기하 평균을 이용한 선행 연구 [10]에서는 그림 4에서와 같이 로그 공간에서 ρ는 $$ u={\left(\mathrm{1,1},1\right)}^T/\sqrt{3}$$에 직교하며, 식 11과 같이 투영자 $$ P_u^{\perp }$$를 정의하였다.

Fig. 4.

Relationship between ρ and u in log space [10]

$\[ P_u^{\perp }=I-u{u}^T=U^{T}U, \]$

(11)

여기서 U는 2×3 크기의 직교 행렬이며, 식 12에서와 같이 U는 χ = 2×1 좌표계로 로그 공간 ρ_k를 로그 공간으로 회전시키고 있다. 최종 불변 영상은 식 7과 식 13에 의해 구해지며, 주요 결과 영상들과 불변 영상은 그림 5에서 보이고 있다.

$\[ \begin{array}{cc}\chi \equiv U\rho ,\hfill & U=\left[\begin{array}{ccc}\frac{1}{\sqrt{2}}\hfill & \frac{-1}{\sqrt{2}}\hfill & 0\hfill \\ \frac{1}{\sqrt{6}}\hfill & \frac{1}{\sqrt{6}}\hfill & \frac{-2}{\sqrt{6}}\hfill \end{array}\right].\hfill \end{array} \]$

(12)

$\[ \Im ={\chi }_{1}cos\left(\theta \right)+{\chi }_{2}sin\left(\theta \right). \]$

(13)

Fig. 5.

Images obtained by (9) to (13)

그림 5의 영상들은 그림 3(a)의 RGB 칼라 영상을 이용하여 획득한 결과 영상들로 최종 불변 영상은 투영 각도 θ = 35°로 출력되었다.

Ⅲ. 제안하는 불변 영상

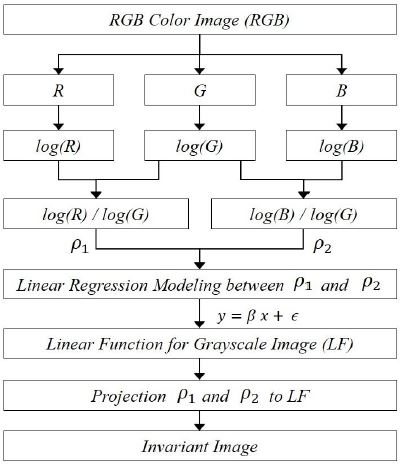
본 논문에서 제안하는 불변 영상을 획득하는 과정은 그림 6과 같다. 먼저 식 14의 RGB 칼라 영상의 각 채널의 밴드 비의 로그 ρ_k=1,2 간의 선형 회귀를 통해 그레이스케일 라인(line)으로 투영 시 최적의 기울기를 획득한다.

Fig. 6.

Proposed process for acquiring the invariant image

선형 회귀는 집합 $$ {\left\{y_i,x_{i1},\dots ,x_{ip}\right\}}_{i=1}^n$$에 대해 y_i와 p개의 변수 x_i 사이의 선형 관계를 모델링하며 [11], 1차 함수인 경우 식 15와 같이 직선의 방정식을 구할 수 있다. 식 14에서 계산된 2차원 행렬 ρ₁과 ρ₂ 간의 분포는 그림 7에서 보이고 있으며, 그림 3(a)의 RGB 칼라 영상을 이용하였다. 또한 2차원 행렬 ρ₁과 ρ₂를 각각 1차원 벡터로 변환한 후 선형 회귀를 수행하면 기울기 β와 종속 변수 y의 오차 요인인 ϵ을 획득할 수 있다. 그림 7에서 보이는 일차 함수는 최종 그레이스케일 영상을 나타내며, 일차 함수의 기울기 β는 -1.0396, ϵ은 1.9966으로 계산되었다. 그림 8은 그림 3(a)의 RGB 칼라 영상을 이용한 제안한 방법의 불변 영상들을 보이고 있다.

Fig. 7.

istribution between ρ1 and ρ2, and the linear regression-based linear function

Fig. 8.

Invariant images obtained by (16)

Ⅳ. 실험 및 고찰

본 논문의 2장에서 그림자 검출 및 복원을 위한 특징요소 중의 하나인 불변 영상을 획득하는 기존의 방법들을 설명하였다. 3장에서는 제안하는 방법인 RGB 칼라 영상의 각 채널의 밴드 비의 로그 {log(R/G),log(B/G)} 간의 선형 회귀 기반의 최적의 기울기로 일차 함수를 검출한 후 밴드 비의 로그 ρ_k의 화소들을 일차 함수, 즉 그레이스케일 영상 라인으로 투영시켜 불변 영상을 획득하는 과정을 제안하였다.

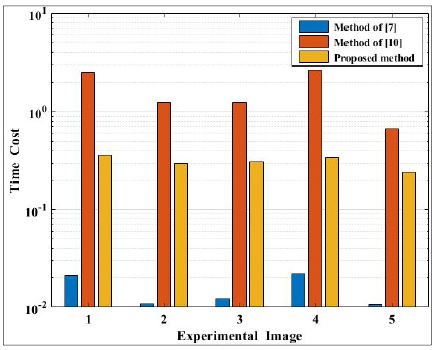
그림 9는 기존의 방법과 제안하는 방법으로 획득한 불변 영상들을 보이고 있다. 그림 9(b) 영상들은 [7]의 방법으로 식 2의 α 값은 표 1의 α 값들의 평균값을 적용하여 출력된 불변 영상들이다. 그림 9(c)와 (d)는 Finlayson이 제안한 방법으로 그림 4에서와 같이 투영자 $$ P_u^{\perp }$$를 이용하여 밴드 비의 로그 ρ_k를 회전시켜 불변 영상을 획득하고 있다. 이때 투영 각도 θ는 그림 1의 Lambertian surface에 반사되는 각도로 식 7과 같이 엔트로피 최소화 기반으로 추정된다. 그림 9(e)는 제안하는 방법으로 밴드 비의 로그 영상 ρ_k 정보 간의 선형 회귀를 통해 식 15와 같이 일차 함수를 취득하고, 식 16을 이용하여 ρ_k를 그레이스케일 영상 라인으로 투영시켜 불변 영상을 획득하였다. 그림 10은 기존 방법들과 제안방법의 불변 영상 획득 시간 비용을 비교한 것으로 [7]의 방법, 제안 방법 및 [10]의 방법 순으로 계산 복잡도가 낮음을 알 수 있었다.

Fig. 9.

Comparison of invariant images; (a) experimental images; (b) method of [7]; (c) method of [8]; (d) method of [10]; (e) proposed method

Table 1.

Choice of α value for Point Grey camera [7]

Fig. 10.

Time cost comparison of the existing and proposed method

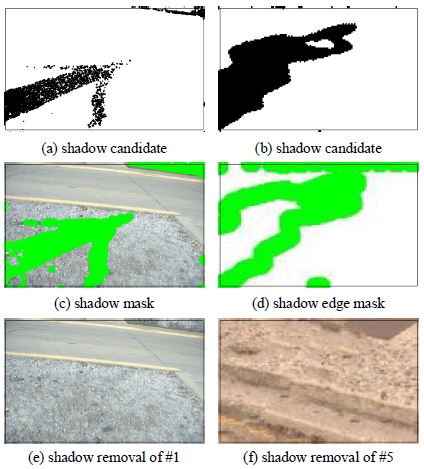
그림 10에서 [7]의 방법이 불변 영상 획득을 위한 시간 비용이 우수하지만 α의 값 추정이 적응적이지 않고, 그림자 제거 시 별도의 그림자 검출 과정이 필요하다. 반면 [10]의 방법과 제안하는 방법은 불변 영상을 이용한 그림자 검출 및 제거 과정에서 불변 영상을 활용한다는 장점을 가진다. [10]의 방법은 식 10의 밴드 비의 로그 ρ_k를 그레이스케일 영상 라인으로 투영하기 위해 0°부터 180°사이의 엔트로피 최소값으로 투영 각도 θ를 추정하였다. 반면 제안하는 방법은 ρ_k 간의 선형 회귀를 통해 최적의 그레이스케일 영상라인을 획득하고, 이 일차함수로 ρ_k를 투영하였다. 그림 10에서 보여주듯이 [10]의 방법보다 제안하는 방법이 계산 복잡도가 낮음을 알 수 있다. 그림 11(a)와 (b)는 제안하는 방법으로 획득한 불변 영상과 그레이스케일 영상간의 차이를 통해 얻어진 그림자 후보군들이며, 그림 11(c)부터 (f) 까지는 [12]의 방법으로 그림자 영역 또는 그림자 에지 영역을 이용하여 그림자가 제거되고 복원된(re-integrated) 영상들을 보이고 있다. 그림 11의 결과 영상들에서 보여주듯이 그림자 제거 및 복원을 위해서는 그림자 후보군 검출이 정확하게 이루어져야 한다. 향후, 본 논문에서 제안한 불변 영상을 이용한 그림자 후보군 검출 정확도를 높이고, 그림 11(e)와 (f)와 같이 부정확한 그림자 제거 및 복원을 개선하는 연구를 계속하고자 한다.

Fig. 11.

Shadow removal images by [12]

Ⅴ. 결론 및 향후 연구

본 논문에서는 단일 자연 영상에 포함된 그림자를 검출하고 제거하는 주요 특징요소 중의 하나인 불변 영상을 획득하는 기존의 방법들을 기술하였고, 밴드 비의 로그 영상들 간의 선형 회귀 기반의 그레이스케일 영상 라인을 추정하여 불변 영상을 획득하는 방법을 제안하였다. [7]의 방법은 카메라의 종류마다 식 2의 α 값을 추정해야 하는 단점을 가진다. [10]의 방법과 제안하는 방법은 밴드 비의 로그 영상들을 그레이스케일 영상 라인으로 투영시키는 방법론은 동일하지만, 제안하는 방법이 선형 회귀 기반 그레이스케일 영상 라인을 획득함으로서 엔트로피 최소화를 통한 투영 각도를 계산하는 [10]의 방법보다 계산 복잡도를 줄일 수 있었다. 향후, 불변 영상 기반의 그림자 영역 검출의 정확도를 향상시키는 연구와 [12]의 그림자 제거 및 복원 과정을 개선하고자 한다.

Acknowledgments

이 성과는 2017년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2017R1C1B5018143).

References

• M. Xu, J. Zhu, Lv P., B. Zhou, M. F. Tappen, and R. Ji, “Learning-Based Shadow Recognition and Removal From Monochromatic Natural Images”, in Proceedings of IEEE Transactions on Image Processing, 26(12), p5581-5824, Dec.), (2017. [https://doi.org/10.1109/TIP.2017.2737321]
• Zhj, J., Samuel, K. G. G., Masood, S. Z., Tappen, M. F., “Learning to recognize shadows in monochromatic natural images,”, in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), p223-230, San Francisco, CA, June), (2010. [https://doi.org/10.1109/CVPR.2010.5540209]
• J.-F. Lalonde, A. A. Efros, and S. G. Narasimhan, , in European Conference on Computer Vision (ECCV), LNCS, 6312, p322-335, Sep.), (2010.
• K. H. Park, and Y. S. Lee, “Definition and Analysis of Shadow Features for Shadow Detection in Single Natural Image,”, The Journal of Digital Contents Society, 19(1), p165-171, Jan.), (2018.
• Wikipedia, Planckian locus [Internet], Available: https://en.wikipedia.org/wiki/Planckian_locus.
• Wikipedia, Lambertian reflectance [Internet], Available: https://en.wikipedia.org/wiki/Lambertian_reflectance.
• W. Maddern, A. Stewart, C. McManus, B. Upcroft, W. Churchill, and P. Newman, “Illumination invariant imaging: Applications in robust vision-based localisation, mapping and classification for autonomous vehicles,”, in Proceedings of the Visual Place Recognition in Changing Environments Workshop, IEEE Intl. Conf. on Robotics and Automation, (2014).
• M. S. Drew, G. D. Finlayson, and S. D. Hordley, "Recovery of Chromaticity Image Free from Shadows via Illumination Invariance", in IEEE Workshop on Color and Photometric Methods in Computer Vision (ICCV), p32-39, Oct.), (2003.
• G. D. Finlayson, M. S. Drew, and C. Lu, “Intrinsic Images by Entropy Minimization,”, in European Conference on Computer Vision (ECCV), LNCS, 3023, p582-595, May), (2004.
• G. D. Finlayson, M. S. Drew, and C. Lu, “Entropy Minimization for Shadow Removal”, International Journal of Computer Vision, 85(1), p35-57, Oct.), (2009. [https://doi.org/10.1007/s11263-009-0243-z]
• Wikipedia, Linear regression [Internet], Available: https://en.wikipedia.org/wiki/Linear_regression.
• A. Criminisi, P. Perez, and K. Toyama, “Object Removal by Exemplar-Based Inpainting”, in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Madison, WI, p739-743, June), (2003. [https://doi.org/10.1109/CVPR.2003.1211538]