빅데이터 군집 분석을 이용한 학습성취도 예측 : 종단 연구를 중심으로

Ⅰ. 서론

최근 정보량이 급격히 증가함에 따라 국내는 물론 세계 각국에서 자료를 관리하고 분석하여 가치 있는 자료로 만들기 위한 노력을 기울이고 있다. 빅데이터란 데이터를 관리, 분석하여 대용량으로 취합하는 형태로 공공기관에서 공개한 양질의 자료를 이용하여 사회적 가치 창출을 할 수 있다. 특히, 빅데이터 분석 기술은 선호도가 비슷한 상품을 추천하는 상업 분야나 교육 등의 다양한 분야에 적용이 되어 연구 성과를 보여 왔다[1, 2].

2016년도에 조사가 완료된 한국아동·청소년패널조사(KCYPS-Korea Children and Youth Panel Survey)[3]는 2010년에 선정된 초등학교 1학년과 4학년, 중학교 1학년의 3개 연령집단 표본 7071명을 대상으로 2016년 까지 7개년에 걸쳐 실시된 종단조사 연구이다. KCYPS를 이용한 연구는 많으나 빅데이터를 이용한 연구로는 데이터마이닝을 활용한 다문화수용성 결정요인의 연차별 분석[4], 신경망 분석을 활용한 학교폭력의 예측요인 분석 및 해결방안 모색[5], 군집 분석을 활용한 아동의 학교생활적응 유형 분류와 영향요인 연구[6] 등이 있다.

본 연구에서는 KCYPS 자료 중 중학교 1학년 패널 자료를 사용하여 빅데이터 군집 분석을 통하여 종단적으로 학습성취도를 예측하는 방법을 제안한다. 중학교 1학년, 중학교 3학년, 고등학교 3학년, 대학교 1학년의 패널 자료를 학습 집합과 테스트 집합으로 분류한다. 학습 집합을 대상으로 군집하고 종단 연구를 통하여 7년에 걸쳐서 나타내는 학습성취도를 분석하고, 군집된 그룹의 특징을 추출한다. 다음으로 학습한 자료를 기반으로 테스트 집합의 학생들에 대해 그룹의 특징을 이용하여 비슷한 학습 습관 유형의 그룹으로 분류한 후, 7년에 걸쳐 나타나는 학습성취도를 예측한다.

학습 집합을 군집하는 빅데이터 군집 방법으로는 Kmeans 군집 방법[7], 신경망(Artificial Neural Network)[8], SVD(Support Vector Machine)[9] 등의 방법이 있다. 본 논문에서 제안한 방법에서는 군집을 위해 대용량 자료에서도 수행 속도가 빠른 Kmeans 군집 방법을 중학교 1학년의 패널 자료를 대상으로 사용한다. 또한, 테스트 집합의 학생을 K-최근접 이웃 기법(K_NN-K-Nearest Neighbor)을 이용하여 학습 습관이 비슷한 학생들이 모인 그룹으로 분류한 후, 가장 유사도가 비슷한 이웃 학생을 선정한다. 이러한 경우, 유사도 계산 방법을 어떤 방법을 사용하는가에 따라 정확도에 있어서 많은 차이를 나타낸다. 유사도 계산 방법으로는 유클리드 거리(E​uclidean distance), 코사인 유사도(Cosine similarity), 피어슨 상관 계수(Pearson correlation coefficient) 등 여러 방법이 있다[10]. 유사도 계산 방법의 성능은 자료의 크기와 희소성의 정도에 따라 크게 달라지므로 실험을 통하여 가장 정확도가 높은 유사도 계산 방법을 제안한 방법에 적용한다.

본 논문은 다음과 같은 순서로 구성되어 있다. 2장에서는 한국아동·청소년패널조사자료를 정규화하고 Kmeans알고리즘을 사용하여 군집하는 방법을 기술한다. 3장에서는 2장에서 군집된 그룹들을 대상으로 군집 분석을 하여 중학교 1학년의 학습 습관이 종단적으로 어떤 영향을 미치는가를 기술한다. 4장에서는 그룹의 특징을 추출하고 학습성취도를 종단적으로 예측하는 방법을 기술한다. 5장에서는 4장에서 기술된 방법의 성능 평가를 기술하고, 6장에서는 결론을 기술한다.

Ⅱ. Kmeans알고리즘을 이용한 군집과 정규화

한국아동·청소년패널조사 자료를 기반으로 연구한다면 중학교 1학년 때의 학습 습관이 고등학교, 대학교의 학습성취도에 어떠한 영향을 미치는가를 규명할 수 있다. 그러나 개인별로 중학교 1학년의 학습 습관이 성장하면서 학습성취도에 어떤 영향을 끼치는가를 분석할 경우, 개인별 상황과 변인에 따라 다르기 때문에 정확한 결론을 얻기 어렵다. 본 논문에서는 이를 해결하기 위한 방법으로 중학교 1학년 학생들을 대상으로 비슷한 학습 습관을 갖는 학생들을 군집하고, 군집된 학생들의 학습 습관이 종단적으로 학습성취도에 어떠한 영향을 미치는가를 연구하고자 한다. 대상이 가지고 있는 정보의 유사성에 따라 대상을 분류하는 기법을 군집화(Clustering)이라고 하며, 본 논문에서 제안한 방법에서는 비계층적 군집 분석 방법을 사용하는 Kmeans 군집 분석을 이용하여 군집한다. Kmeans 군집 분석 방법은 계산량이 적기 때문에 대용량 자료도 빠르게 처리할 수 있는 장점이 있기 때문이다.

2-1 Kmeans 알고리즘

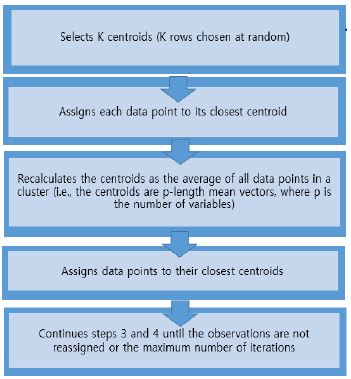
군집은 같은 군집 내의 객체들과는 비슷한 성향을 나타내고, 다른 군집의 객체들과는 다른 특성을 나타내는 집합이다. 그림 1은 Kmeans 알고리즘을 나타낸다.

Fig. 1.

Kmeans algorithm

Kmeans 군집 분석은 분할기법의 하나로, n개의 객체가 주어진 경우 이를 군집으로 분류하기 위하여 K개로 분할을 시도한다[11]. 그림 1의 알고리즘은 제곱 오차 함수를 최소화할 수 있도록 K개의 분할을 만든다. 식 (1)은 제곱오차를 적용하여 객체를 임의의 K개의 그룹으로 분류하기 위한 식이다.

$\[ E=\sum _{i=1}^K\sum _{p\in c_i}{\left|p-m_i\right|}^2 \]$

(1)

식 (1)에서 E는 데이터베이스에서 모든 학생들의 제곱오차를 합한 값이며, n은 전체 학생수이고 K는 군집의 수, t는 반복의 수이다. 또한, p와 m_i는 다차원이며 p는 해당 학생을 나타내는 공간의 점이고, m_i는 군집 c_i의 평균이다.

2-2 군집을 위한 정규화

Kmeans 알고리즘을 사용하여 군집할 대상은 전국의 중학교 학생들을 대상으로 2010년부터 2016년까지 7년 동안 반복적인 추적조사를 실시한 자료 중 중학교 1학년 자료이다. 2010년 중학교 1학년을 대상으로 여러 가지 변인을 추출하여 비슷한 학들끼리 군집을 실시한다. 아이디(ID)를 기본으로 공부 습관에 관한 변인들을 추출 한다. 추출된 변인은 아이디를 제외하고 17개의 변인이다. 표 1은 17개의 변인과 변인설명, 그리고 변인값을 나타낸다.

Table 1.

Seventeen variables of the first grade at middle school

표 1의 변인을 기준으로 2351명의 아이디를 포함한 18개의 변인에 대한 평가한 값을 추출한다. 추출한 자료는 결측치가 없었으므로 그대로 결측치를 처리하지 않고 사용한다. 표 2는 17개의 변인에 대해 중학교 1학년의 학생들이 평가한 값의 예를 나타낸다.

반면, 표 2의 자료를 가공하지 않고 학생이 평가한 값을 기준으로 군집할 경우 값의 가중치가 다른 변인들과 비교하여 상대적으로 얼마나 큰가 작은가를 반영할 수 없으므로 비슷한 학생을 찾았을 경우 정확도가 낮아진다. 예를 들어, 표 2에서 ID 14201의 INT2A07w1은 ‘2’의 값, ID 14204의 INT2A02w1도 ‘2’로 값은 값을 나타낸다. 그러나 INT2A07w1의 ‘2’와 INT2A02w1의 ‘2’는 다른 가중치를 나타낸다. 따라서 변인에 대해 평가한 값이 다른 학생들이 평가한 값과 비교하여 어떤 가중치를 나타내는가를 표시할 필요가 있다. 따라서, 학생이 변인에 대해 평가한 값이 다른 학생들과 비교하였을 경우 상대적으로 어느 정도의 위치에 있는가를 가중하여 군집을 해야 한다. 이와 같이 평가한 값에 대하여 상대적으로 얼마의 가중치를 나타내는가를 계산하기 위하여 정규화를 실시한다.

Table 2.

Examples of values assessed by first grade students at middle school for 17 variables

정규화를 위한 방법으로 z점수(z_score)를 이용하여 원점수의 상대적 위치를 계산한다. z점수란 특정 점수가 평균으로부터 얼마나 떨어져 있는가를 알려주는 함수로 평균과 표준편차를 이용해서 계산하는 일종의 표준점수이다. ‘+’는 특정 점수가 평균보다 클 때를 나타내고, ‘–’는 특정 점수가 평균보다 작을 때를 나타낸다. 자료 집합의 모든 원소에 대해 각각의 z점수를 계산하여 자료를 정규화한다.

이와 같이 정규화된 결과는 서로 다른 변인들의 평가값에 대해 서로 상대적인 비교를 가능하게 한다. z점수의 평균은 항상 0, 표준편차는 1을 나타낸다. 표 3은 표 2를 z점수에 의하여 정규화한 결과를 나타낸다.

2-3 Kmeans 알고리즘을 이용한 군집

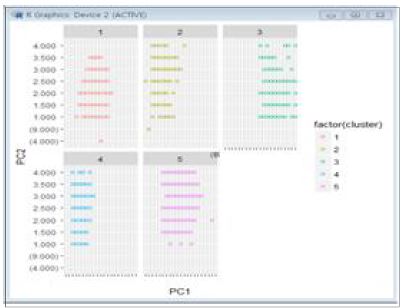
표 3과 같이 정규화를 한 후 Kmeans 알고리즘에 의하여 중학교 1학년 자료를 5개의 군집으로 분류한다. 군집 결과, 각 그룹의 크기는 602, 329, 299, 408, 713 등이다. 그림 2는 군집된 5개의 그룹에 대한 결과를 나타낸다. 그림 2와 같이 군집된 그룹을 그래프로 나타내기 위하여 17개의 변인 중 표준편차가 큰 10개의 변인을 추출하고, 그 중 5개 변인에 대한 평가값의 평균을 PC1으로 지정한다, 그리고, PC2는 나머지 5개의 변인에 대한 평가값의 평균을 나타낸다.

Table 3.

Normalization by z_score

Fig. 2.

Five groups clustered by Kmeans algorithm

Ⅲ. 군집 분석

Kmeans 알고리즘에 의하여 군집된 중학교 1학년 학생들은 비슷한 학습 습관을 나타내므로 군집별 학생들의 학습 습관 특징을 종단적으로 분석할 수 있다[12]. 먼저, 같은 군집의 학생들이 2년 후인 중학교 3학년이 되었을 경우와 고등학교 3학년이 되었을 경우의 학습성취도의 특징을 분석한다. 다음으로, 대학교 1학년이 되었을 경우의 학습성취를 통한 대학 및 전공 만족도를 분석함으로써 중학교 1학년 때의 학습 습관이 중학교 3학년, 고등학교 3학년, 그리고 대학교 1학년의 학습성취도에 어떠한 영향을 주는가를 분석한다.

3-1 군집된 그룹별 학습 습관의 특징 분석

표 4는 그림 2와 같이 군집된 그룹의 각 변인에 대한 중앙값을 나타낸다. 표 5는 표 4를 기반으로 분석한 각 그룹별 특징과 학습 습관이 좋은 순위를 나타낸다.

Table 4.

Size and median of each group

Table 5.

Characteristics of each group

표 5에서 군집된 각 그룹별 특징의 특이사항을 보면 학습 습관이 가장 좋은 Group2의 경우 학업시간 관리를 비롯한 모든 변인이 대부분 우수하나 학교 공부의 중요성에 대해서는 다소 낮은 평가를 하였다. Group3은 전반적으로 학습 습관이 가장 좋지 않으나 자기 통제 항목에서는 Group1보다는 높은 평가를 하였다.

3-2 군집된 그룹별 학습성취도의 특징 종단 분석

2010년 중학교 1학년의 데이터를 기반으로 비슷한 학습 습관을 갖는 5개의 그룹으로 군집된 학생들이 중학교 3학년이 되는 2012년도에는 각 그룹의 학생들이 국어, 수학, 영어, 과학에 대하여 어떠한 성적 분포를 나타내는가를 분석할 수 있다. 표 6은 2012년도인 중학교 3학년 학생들의 성적 분포를 분석하기 위하여 추출한 변인과 변인 설명을 나타낸다.

Table 6.

Variables derived from the third year at middle school students

표 7은 2010년의 자료에 기반하여 그림 2와 같이 군집된 학생들이 중학교 3학년이 되는 2012년도에 국어, 수학, 영어, 과학에 대해 평가한 각 과목의 평균을 나타내는 표이다. 표 5의 학생들에 비하여 Group1은 36명, Group2는 21명, Group3은 25명, Group4는 15명, 그리고 Group5는 35명의 학생이 평가를 하지 않아서 중학교 1학년 자료에 비하여 그룹의 크기가 감소하였다. 표 6과 표 7을 비교하면 학습 습관이 우수한 학생들의 그룹인 Group2가 중학교 3학년이 되었을 때도 모든 성적이 가장 높았으며, 학습 습관이 가장 안좋은 그룹인 Group3의 경우 성적이 최하위였다. 그림 3은 표 7을 기반으로 그려진 그룹별 4과목의 평균을 나타낸다. 그림 3에서 4과목 중 수학 과목은 국어 과목과 비교하였을 때 학습 습관이 가장 좋았던 Group2에서는 국어와 수학의 차이가 다른 그룹보다 작다는 것을 알 수 있다. 즉, 학습 습관의 영향을 가장 많이 받는 과목은 수학이며, 학습 습관에 가장 적게 영향을 받는 과목은 국어라는 것을 알 수 있다.

Table 7.

Average of each subject group for the third grade at middle school

Fig. 3.

Average of 4 subjects by group

다음으로, 2015년 고등학교 3학년과 2016년 대학교 1학년이 평가한 여러 변인 중 학습성취도에 관한 변인 7개와 6개를 각각 추출하여 비슷한 학생들끼리 군집된 그룹의 학생들이 어떠한 학습성취도를 나타내는가를 분석하였다. 표 8은 고등학교 3학년 자료로부터 추출한 7개 변인과 대학교 1학년 자료로부터 추출한 6개의 변인을 나타낸다.

Table 8.

Variables extracted from third grade at high school and first grade at university

표 8의 변인을 기준으로 학습성취도와 삶의 만족도를 고등학교 3학년 때와 대학1학년으로 구분하여 그룹별로 비교한다. 고등학교 3학년이 되는 자료는 중학교 3학년 학생들의 자료에 비하여 Group1은 26명, Group2는 34명, Group3은 33명, Group4는 19명, 그리고 Group5는 51명의 학생이 평가를 하지 않아서 중학교 3학년 자료에 비하여 그룹의 크기가 감소하였다. 또한, 대학교 1학년이 되는 자료도 고등학교 3학년 학생들의 자료에 비하여 Group1은 182명, Group2는 92명, Group3은 90명, Group4는 128명, 그리고 Group5는 213명의 학생이 평가를 하지 않아서 자료의 수가 대폭으로 감소하였다. 고등학생이 대학생이 되면서 재수를 하는 학생들이 발생하는 등 평가를 하지 못한 여러 가지 원인이 있을 것으로 추정한다.

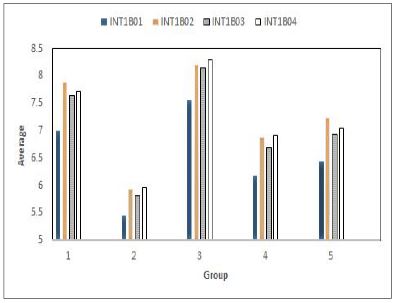
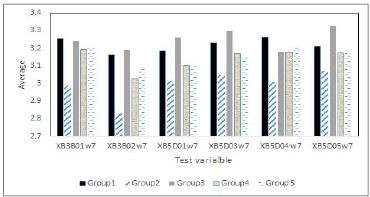
표 9는 고등학교 3학년 자료와 대학교 1학년 자료 중 표 8의 변인에 대해 평가한 값의 평균을 나타낸다. 그림 4는 표 9에서 2015년도 고등학교 3학년 자료의 그룹별 학습성취도 및 삶의 만족도의 변인에 대한 그룹 별 평균을 나타낸다.

Fig. 4.

Achievement of learning by group for high school 3rd grade data

Table 9.

Average for each variable by group

그림 4에서 중학교 1학년 때의 학습 습관은 고등학교 3학년이 되었을 때도 연관이 되어서 학습 습관이 좋았던 학생의 학습성취도가 고등학교 3학년 때도 높았다. 특히, 성적의 주관적 평가 변인에서 Group2에 속한 학생들이 평가한 값의 평균이 다른 그룹들과 비교할 때 현저하게 높았다. 그러나 숙제를 빠짐없이 하는 부분에서는 다른 그룹에 비하여 높지 않은 평가를 하였다. 또한, 성적의 만족도 변인에서는 Group2가 다소 높긴 하지만 전반적으로 모든 그룹의 학생들이 현재의 성적보다 향상되기를 희망하였다.

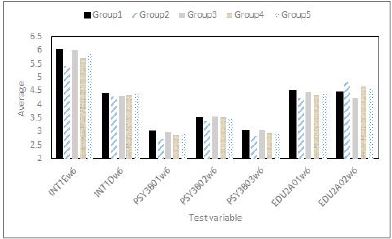
그림 5는 표 9에서 2016년도 대학교 1학년 자료 중 대학 및 전공 만족도의 변인에 대한 그룹별 평균을 나타낸다. 표 10은 비슷한 학습 습관의 학생들이 고등학교 3학년과 대학교 1학년이 되었을 경우의 학습성취도를 기술한 표이다.

Fig. 5.

The comparison of university satisfaction for the first grade at university

Table 10.

Characteristics of learning achievement by group

Ⅳ. 그룹의 특징 추출과 학습성취도 종단 예측

중학교 1학년 학생의 학습 습관에 대한 변인의 평가값을 안다면 그 학생을 5개 그룹 중 하나의 그룹으로 분류할 수 있다. 이를 위하여 그림 2와 같이 군집된 학생들을 기반으로 그룹의 특징을 추출하는 것이 필요하다. 즉, 학생이 평가한 값과 그룹의 특징을 비교하여 가장 유사한 그룹으로 학생을 분류하고, 그룹에 속한 이웃 학생을 기반으로 학습성취도를 예측할 수 있다.

4-1 그룹의 특징 추출

그림 2와 같이 군집된 학생들을 기반으로 각 그룹의 특징 벡터를 추출할 수 있다. 그룹의 특징을 추출하기 위해 중학교 1학년이 학생들이 학습 습관에 대해 평가한 17개의 각 평가 문항에 대해 평가한 값을 가중치로 정의한다. 각 그룹의 학생들이 문항에 대해 평가한 값의 각 항목 별 평균을 사용하여 17개의 변인으로 이루어진 특징 벡터를 산출한다. 식 (2)는 학생이 평가한 변인에 대해 평가한 값을 행렬 V_ck로 나타낸 식이다. V_ck는 k번째 군집에 속한 n명의 학생과 m개의 변인으로 구성된 행렬이다. 식 (2)에서 v_ckij는 i번째 학생이 변인 j에 대해 평가한 값이다.

$\[ V_{ck}=\left[\begin{array}{c}{v}_{c{k}_{11}}\cdot \cdot \hfill \\ \cdot \cdot \hfill \\ v_{c{k}_{i1}}\cdot \cdot \hfill \\ v_{c{k}_{n1}}\cdot \cdot \hfill \end{array}\begin{array}{c}{v}_{c{k}_{1j}}\cdot \cdot \hfill \\ \cdot \cdot \hfill \\ v_{c{k}_{ij}}\cdot \cdot \hfill \\ v_{c{k}_{nj}}\cdot \cdot \hfill \end{array}\begin{array}{c}{v}_{c{k}_{1m}}\hfill \\ \cdot \cdot \hfill \\ v_{c{k}_{im}}\hfill \\ v_{c{k}_{nm}}\hfill \end{array}\right] \]$

(2)

식 (2)에서와 같이 k번째 군집에 속한 학생이 평가한 변인에 대해 평가한 값을 행렬 V_ck로 나타냈을 경우 k번째 그룹의 특징을 나타내기 위한 요소를 식 (3)으로 표현할 수 있다.

$\[ w_{ckINT2A01w1}=\sum _{i=1}^n\left(v_{{ck}_{i1}}\right)/n \]$

(3)

식 (4)은 k번째 그룹의 특징을 나타낸다. 식 (4)에서 w_ckINT2A01w1은 식 (3)과 같이 INT2A01w1의 변인에 대하여 k번째 군집의 학생들이 이 변인에 대하여 평가한 값의 평균을 나타낸다.

$\[ f_{ck}=\left\{w_{ck}INT2A01w1,w_{ck}INT2A02w1,...,w_{ck}INT2D03w1\right\} \]$

(4)

표 11은 식 (2), 식 (3), 식 (4)을 이용하여 정의한 그룹별 특징 벡터를 나타낸다.

Table 11.

Group feature vectors

4-2 그룹의 특징을 이용한 학습성취도 예측

중학교 1학년인 새로운 학생이 표 1의 변인에 대해 평가를 하였을 경우, 표 11과 같이 추출된 그룹의 특징을 기반으로 이 학생을 가장 성향이 비슷한 그룹으로 분류한다. 이 학생이 분류된 그룹의 학생들의 속성을 기반으로 이 학생이 중학교 3학년, 고등학교 3학년, 고등학교를 졸업한 후 대학에 간 경우의 학습성취도와 대학 및 전공 만족도를 예측할 수 있다.

1) K-최근접 이웃 기법을 이용한 학생 분류

추출한 그룹의 특징을 기반으로 새로운 학생을 5개 그룹 중 한 그룹으로 분류하기 위하여 K-최근접 이웃 기법을 사용한다. K-최근접 이웃 기법의 기본사상은 분류하고자하는 새로운 학생과 유사한 학습용 집합에 있는 K개의 관찰치를 확인하는 것이다[13, 14]. 인접한 학생들을 사용하여 새로운 학생을 이들 이웃한 자료들 중에서 우세한 집단으로 분류한다. 여기서 가장 중요한 문제는 예측 변수에 기초하여 학생들간의 거리를 어떻게 측정하는가에 있다. 학생들간의 유사도를 계산하는 방법은 유클리드 거리와 코사인 유사도, 그리고 피어슨 상관 계수 등 여러 방법이 있다.

유클리드 거리를 이용한 유사도 측정방법은 가장 일반적인 방법으로 두 레코드 v_ck1, v_ck2,...,v_ckp와 u₁, u₂,...,u_p사이의 거리를 식 (5)로 측정한다[15].

$\[ d\left(v_{ck}, u\right)=\sqrt{\sum _i{\left(v_{cki}-u_i\right)}^2} \]$

(5)

코사인 유사도는 내적공간의 두 벡터 간 각도의 코사인 값을 이용해 측정된 벡터 간의 유사한 정도를 의미한다. 벡터의 크기가 아니라 방향의 유사도를 판단하는데 주 목적이 있으며, 식 (6)으로 정의된다[16].

$\[ sim\left(v_{ck},u\right)=\frac{\sum _i{v}_{cki}{u}_i}{\sqrt{\sum _i{\left(v_{cki}\right)}^2}\sqrt{\sum _i{\left(u_i\right)}^2}} \]$

(6)

피어슨 상관 계수는 두개의 수치들의 집합이 있을 때 이 두개의 수치들은 각각의 순서쌍에 대해서 연결 관계가 있다고 할 때 두 수치가 서로 관련이 있는지를 확인하는 방법이다. 식 (7)은 피어슨 상관 계수를 이용하여 학생간의 유사도를 계산하는 식이다.

$\[ sim\left(v_{ck},u\right)=\frac{\sum _{i\in I_v\cap I_v}\left(v_{cki}-{\mu }_v\right)\left(u_i-{\mu }_u\right)}{\sqrt{\sum _{i\in I_v\cap I_u}{\left(v_{cki}-{\mu }_v\right)}^2}\sqrt{\sum _{i\in I_v\cap I_u}{\left(u_i-{\mu }_u\right)}^2}} \]$

(7)

본 논문에서는 식 (5), 식 (6), 식 (7)의 유사도들 중 희소한 데이터집합에서 가장 높은 정확도를 나타내는 코사인 유사도를 이용하여 학생간의 유사도를 계산한다.

새로운 학생과 비슷한 이웃을 선정하기 위하여 K를 지정해야 한다. K의 값이 증가될수록 분류의 정확도가 높아지다가 일정 수이상이 되면 정확도는 변함이 없다. 따라서 정확도가 일정해지는 K의 값을 찾아서 이 값을 이웃의 수로 지정한다. 본 논문에서는 K의 값을 10을 지정하여 새로운 학생의 이웃을 찾고, 이 이웃 학생을 기반으로 새로운 학생에 대한 학습성취도를 종단적으로 예측한다. 표 12는 새로운 학생이 17개의 변인에 대해 평가한 값이다.

Table 12.

17 variables evaluated by new student

표 12의 학생은 표 1의 기준에서 학교 공부에 중요한 의미를 두나 공부가 지루하면 끝가지 못하고 공부를 끝날 때까지 공부에 집중하지 못하며 노는 것을 그만두지 못해 공부를 시작하기가 어려운 학생이라는 특성을 갖는다.

표 13은 새로운 학생이 평가한 값과 표 11의 그룹의 특징간의 코사인 유사도를 식 (6)에 따라 계산한 결과이다.

Table 13.

Similarities between a new student and features of each group

표 13을 기반으로 새로운 학생은 Group1로 분류되었다. 표 5에 기술한 Group1의 특징이 전반적으로 학습 습관이 좋지 않고 학업시간관리가 부족하다는 그룹의 특징과 새로운 학생의 특징과 유사한 면이 많다는 것을 알 수 있다.

2) 학습성취도 종단적 예측

새로운 학생을 특정한 그룹으로 분류한 후, 그룹안에 속한 학생들과의 유사도를 계산하여 가장 유사도가 비슷한 이웃을 선정한다. 표 14는 표 12의 새로운 학생이 Group1로 분류되었을 경우 Group1의 학생들 중 가장 유사도가 비슷한 K명의 이웃 학생을 선정하기 위해 식 (5), 식 (6), 식 (7)을 이용하여 계산한 결과를 나타낸다. 표 14에서 ID_P는 피어슨 상관 계수에 의해 추출된 이웃의 ID를, ID_C는 코사인 유사도에 의해 추출된 이웃의 ID, 그리고 ID_E는 유클리드 거리에 의해 추출된 이웃의 ID를 나타낸다. 표 14의 유사도 중 코사인 유사도를 이용하여 10명의 이웃이 변인에 대하여 평가한 값의 평균을 이용하여 이웃을 선정하고, 2년 후인 중학교 3학년이 되었을 때 이웃이 평가한 과목의 점수를 기반으로 새로운 학생이 각 과목에서 획득할 점수를 예측한다.

Table 14.

10 neighbors extracted using similarity calculation formula

표 15는 새로운 학생이 중학교 3학년이 되었을 경우의 국어, 수학, 영어, 과학의 점수와 고등학교 3학년이 되었을 경우 주관적 성적이나 성적에 대한 만족도 등을 예측한 결과이다. 또한, 대학교 1학년이 되었을 경우의 대학과 전공에 대한 만족도도 예측하였다.

Table 15.

Predicting learning achievement

Ⅴ. 성능 평가

본 논문에서 학습성취도 예측 방법의 성능을 평가하기 위하여 K개의 이웃을 지정하여 이웃의 수를 변경시켜가면서 제안한 방법의 성능을 평가하였다. 또한, 본 논문에서 학생간의 유사도를 계산하기 위하여 유클리드 거리를 사용한 경우(Cluster_Eu), 피어슨 상관계수(Cluster_P)를 사용한 경우, 그리고 본 논문에서 제안한 코사인 유사도를 사용한 경우(Cluster_Cos)로 나누어서 예측의 정확도를 비교하였다.

5-3 실험 및 결과

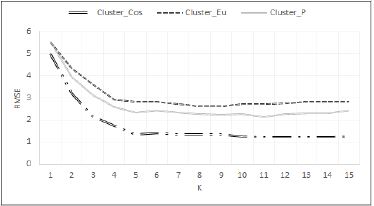
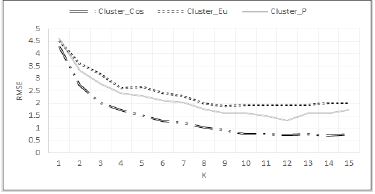
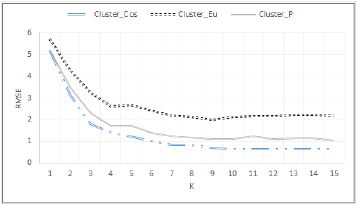
본 논문에서 제안한 방법(Cluster_Cos)의 성능을 평가하기 위해 테스트 집합 학생 851명을 대상으로 중학교 1학년 때 17개의 변인에 대해 평가한 값을 기반으로 각 그룹으로 분류하고, 분류된 그룹의 학생들 중 K명의 이웃을 선정한다. K명의 이웃을 기반으로 테스트 집합의 학생들이 학습성취도에 관한 변인에 대하여 평가할 값을 예측하였다. 그리고 식 (8)을 이용하여 예측한 값과 실제로 평가한 값이 얼마의 차이가 있는가를 계산하고 그 정확도를 평가하였다. 표 16은 이웃의 수 K의 값을 변경함에 따라 본 논문에서 제안한 Cluster_Cos방법, Cluster_Eu, 그리고 Cluster_P방법의 예측 정확도를 비교한 표이다. 그림 6은 중학교 3학년 성적에 대한 예측의 정확도를 식 (8)을 이용하여 비교한 그림이다. 그림 7은 고등학교 3학년 학습성취도에 대한 예측의 정확도를 비교하였으며, 그림 8은 대학교 1학년의 대학 및 전공 만족도에 대한 예측의 정확도를 비교하였다.

Table 16.

The accuracy of the prediction by changing the value of K

Fig. 6.

Accuracy of predicting scores for the third grade at middle school

Fig. 7.

Accuracy of predicting learning achievement for the third grade at high school

Fig. 8.

Accuracy of predicting university satisfaction for the first grade at university and major

표 16과 그림 6에서 보면, 중학교 3학년 성적에 대한 예측의 정확도는 Cluster_Cos 방법이 가장 정확하였으며, Cluster_Eu의 방법은 안정적이기는 하나 Cluster_P의 방법보다 정확도가 낮았다. 또한, 그림 7에서와 같이 고등학교 3학년의 학습성취도는 중학교 3학년 성적에 대한 예측의 정확도보다 높았으며, 중학교 3학년대상 실험의 성능과 같이 Cluster_Cos의 방법이 정확도가 높았다. 마지막으로 대학교 1학년의 대학 및 전공에 대한 만족도에 대한 예측은 고등학교 3학년의 학습성취도를 예측한 경우의 정확도보다 높았으며 다른 경우와 같이 Cluster_Cos의 방법이 정확도가 높았다. 결론적으로 중학교 3학년, 고등학교 3학년, 대학교 1학년으로 올라오면서 변인을 평가하는 학생들의 수가 줄어들면서 보다 평가를 정확하게 하는 이웃들이 증가함에 따라 정확도가 높아진다는 것을 알 수 있다. 또한, 한국아동·청소년패널조사 자료와 같이 학습 자료에 희소성이 거의 없는 자료를 대상으로 유사도를 측정하는 방법은 피어슨 상관 계수를 이용한 방법이나 유클리드 거리를 이용하는 방법보다 코사인 유사도를 이용한 방법이 정확도가 높다는 결과를 보였다. 유클리드 거리를 이용한 방법은 피어슨 상관 계수보다는 정확도가 낮으나 안정적인 결과를 보였다.

Ⅵ. 결론

본 연구에서는 빅데이터 군집 분석을 이용하여 한국아동·청소년패널조사에 기반을 둔 중학교 1학년 패널의 7년에 걸친 자료를 사용하여 학습 습관이 종단적으로 학습성취도와 대학교 1학년시기의 대학 및 전공 만족도에 어떠한 영향을 미치는가와 학생들의 학습성취도를 종단적으로 예측하는 방법을 연구하였다.

종단적으로 분석한 결과, 중학교 1학년 학생의 학습 습관은 중학교 3학년까지 크게 영향을 주었다. 특히, 국어, 수학, 영어, 과학 4과목 모두 영향을 받았으나 가장 영향을 많이 받는 과목은 수학이고, 가장 적게 받는 과목은 국어였다. 군집된 그룹별 고등학교 3학년 때의 학습성취도를 분석하였을 때 중학교 1학년 때의 학습 습관이 좋은 학생이 고등학교 3학년 때도 주관적 성적이 높았다. 반면, 성적에 대한 만족도는 상대적으로 다른 그룹들에 비하여 크게 높지는 않았다. 마지막으로, 대학교 1학년 때의 대학 및 전공 만족도도 학습 습관과 비례하였다. 종합적으로, 중학교 1학년의 학습 습관은 중학교 전반과 고등학교 및 대학교까지 학생들의 성적과 삶의 만족도까지 영향을 미친다는 것을 분석할 수 있었다. 그러나 중학교 1학년 학생들을 5개의 그룹으로만 군집하고 그 군집의 특징을 기반으로 종단적으로 학생들의 학습성취도를 분석함으로 인하여 5개의 특징과는 다른 특징을 보이는 학생들에 대한 분석에는 한계가 있다.

또한, 이와 같은 분석 자료를 기반으로 테스트 집합의 학생의 학습성취도를 종단적으로 예측하였고, 예측의 결과는 코사인 유사도를 이용할 경우 가장 정확도가 높음을 증명하였다. 다만, 학년이 올라갈수록 변인에 대해 평가한 값의 결측치로 인해 발생하는 오차에 대한 해결방법이 필요하다.

향후, Kmeans 군집 방법 뿐 아니라 기계학습에서 사용되는 기존의 다른 군집 방법을 사용하여 학생들을 군집함으로써 보다 정확도가 높은 예측 시스템을 구현하고자 한다.

References

• K. Lee, and E. Park, “The Study of the System Development on the Safe Environment of Children’s Smartphone Use and Contents Recommendations”, Journal of Digital Contents Society, 19(5), p845-852, (2018).
• B. Gupta, M. Goul, and B. Dinter, "Business Intelligence and Big Data in Higher Education: Status of a Multi-Year Model Curriculum Development Effort for Business School Undergraduates, MS Graduates, and MBAs", Journal of CAIS, 36(23), p449-476, (2015).
• National Youth Policy Institute, 1st 7th Survey Data User's guide in Korea Children and Youth Paner Survey(KCYPS), National Youth Policy Institute, Seoul, (2017).
• S. Lee, and Y. Lee, "An Analysis of Annual Changes on the Determining Factors Multicultural Acceptability for Using Data Mining", Korean Journal of Youth Studies, 24(4), p1-26, (2017). [https://doi.org/10.21509/KJYS.2017.04.24.4.1]
• M. Lee, "Analysis of Predictive Factors of School Violence Behavior and Its Solution Using Neural Network Analysis", Korean Journal of Association for Learner centered Curriculum and Instruction, 17(22), p537-561, (2017).
• K. Jung, W. Jeong, "Identifying Latent Classes in Children`s School Adjustment Using the Cluster Analysis and Testing Eco-system Variables as Predictors of Latent Classes", Korean Journal of Forum for youth culture, 32, p119-143, (2012).
• K. Lee, M. Lee, and Y. Kim, “Research on blog search technique using Kmeans”, The Proceeding of Korea Intelligent Information Systems Society - The Fall Conference, p269-275, (2009).
• M. Arif, "Application of Data Mining Using Artificial Neural Network : Survey", International Journal of Database Theory and Application, 8(1), p245-270, (2015). [https://doi.org/10.14257/ijdta.2015.8.1.25]
• M. Chen, S. Mao, and Y. Liu, "Big Data: A Survey", Journal of Mobile Networks and Applications, 19(2), p171-209, (2014). [https://doi.org/10.1007/s11036-013-0489-0]
• Soo Jung Lee, “Performance Analysis of Similarity Reflecting Jaccard Index for Solving Data Sparsity in Collaborative Filtering”, Journal of Computer Education, 19(4), p59-66, (2016).
• S. Kwon, S. Kim, O. Tak, and H. Jeong, “A Study on the Clustering Method of Row and Multiplex Housing in Seoul Using Kmeans Clustering Algorithm and Hedonic Model”, Journal of Intelligence and Information System, 23(3), p95-118, (2017).
• Kabacoff Robert, R in Action-Data analysis and graphics with R, Oreilly & Associates Inc, (2015).
• J. Herlocker, J. A. Konstan, and J. Riedl, “An Empirical Analysis of Design Choices in Neighborhood-Based Collaborative Filtering Algorithms”, Information Retrieval, 5(4), p287-310, (2002). [https://doi.org/10.1023/A:1020443909834]
• Kwang-Sung Jun, Kyu-Baek Hwang, “An Efficient Collaborative Filtering Method Based on k-Nearest Neighbor Learning for Large-Scale Data”, Korea Information Science Society, 35(1C), p376-380, (2008).
• M. Khoshneshin, W. Nick Street, “Collaborative filtering via euclidean, embedding”, The Proceedings of the fourth ACM conference on Recommender systems, p87-94, (2010).
• Jun Wang, Arjen P. De Vries, and Marcel J. T. Reinders, “Unifying user-based and item-based collaborative filtering approaches by similarity fusion”, In SIGIR ’06: Proceedings of the 29th annual international ACM SIGIR conference on Research and development in information retrieval, (2006).
• T. Chai, and R. R. Draxler, “Root mean square error (RMSE) or mean absolute error (MAE)? – Arguments against avoiding RMSE in the literature“, Geoscientific Model Development, 7(3), p1247-1250, (2014). [https://doi.org/10.5194/gmd-7-1247-2014]