[ Article ]

Journal of Digital Contents Society - Vol. 26, No. 3, pp.749-761

ISSN: 1598-2009 (Print) 2287-738X (Online)

Print publication date 31 Mar 2025

Received 27 Dec 2024 Revised 31 Jan 2025 Accepted 12 Feb 2025

DOI: https://doi.org/10.9728/dcs.2025.26.3.749

Financial Fraud Detection System Based on Generative Adversarial Networks

Qing-Quan Fan¹ ; Dong-Ryool Kim² ; Seung-Soo Shin³^{, *}

1Master’s Course, Dept. of Computer and Media Engineering, Tongmyong University, Busan 48520, Korea
2Professor, College of General Education, Tongmyong University, Busan 48520, Korea
3Professor, Dept. of Information Security, Tongmyong University, Busan 48520, Korea

생성적 적대 신경망을 활용한 금융 사기 탐지 시스템

범청천¹ ; 김동률² ; 신승수³^{, *}

1동명대학교 컴퓨터미디어공학과 석사과정
2동명대학교 학부교양대학 교수
3동명대학교 정보보호학과 교수

Correspondence to: ^*Seung-Soo Shin E-mail: shinss@tu.ac.kr

Copyright ⓒ 2025 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Financial fraud is also increasing as financial transactions become increasingly complex. Traditional financial fraud-detection methods require large amounts of training data and significant computational resources. Further, most detection models encounter serious challenges when handling imbalanced data samples, leading to a lack of accuracy in identifying fraudulent transactions. To address this imbalance in financial fraud detection, we propose a generative adversarial network (GAN) system. The proposed GAN generates synthetic fraudulent transaction samples, enhances the diversity of the training data, and improves the model’s accuracy and generalization ability. Experimental results show that the proposed GAN system is more efficient than traditional algorithms and improves the accuracy of credit card fraud detection by 12% compared to the XGBoost algorithm. The GAN system not only provides a new solution for financial fraud detection, but also has the potential to play a crucial role in real-world applications thus contributing to the advancement of financial security.

초록

금융 거래가 점점 복잡해짐으로 금융사기도 더욱 더 증가하고 있다. 전통적인 금융사기 탐지 방법은 대량의 훈련 데이터와 높은 계산 자원을 필요로 하고 대부분의 탐지 모델은 불균형한 사기 샘플을 처리할 때 심각한 문제에 직면해 있으며, 이로 인해 사기 거래를 식별하는 데 정확도가 떨어지고 있다. 금융사기 탐지의 불균형 문제를 해결하기 위해 생성적 적대 신경망 시스템을 제안한다. 제안 기술은 합성된 사기 거래 샘플을 생성하여 훈련 데이터의 다양성을 향상시키고, 모델의 정확도와 일반화 능력을 개선했다. 성능 평가 결과, GANs 시스템은 금융사기 탐지에서 전통적인 알고리즘보다 효율적이고, XGBoost 알고리즘에 비해 정확도가 12% 향상되었다. GANs 시스템은 금융사기 탐지 분야에 새로운 해결책을 제시할 뿐만 아니라, 향후 실제 응용에서 중요한 역할을 하고 금융 보안 분야의 발전에 기여할 수 있을 것이다.

Keywords:

Generative Adversarial Networks, Financial Fraud Detection, Machine Learning, Synthetic Data, Class Imbalance

키워드:

생성적 적대 신경망, 금융 사기 탐지, 기계 학습, 합성 데이터 생성, 클래스 불균형

Ⅰ. Introduction

According to a report by Statista[1], the global losses from online payment fraud in e-commerce were estimated to be $41 billion in 2023, showing an increase compared to the previous year. This figure is expected to rise further to $48 billion by 2024. The COVID-19 pandemic and the accompanying travel restrictions have led to an unprecedented growth in e-commerce, simultaneously opening a window for opportunistic fraudsters. With the development of fintech, the methods of financial fraud have become increasingly diverse, ranging from traditional credit card fraud and identity theft to newer forms such as phishing and fake transactions. Financial fraud not only causes significant economic losses to individuals but also severely impacts financial institutions and the entire financial system. Traditional rule-based and statistical fraud detection methods often struggle to address new and complex fraudulent activities.

In response to these challenges, several machine learning techniques have been employed in financial fraud detection to improve accuracy and efficiency. For instance, Logistic Regression[2] has been widely used in initial fraud detection systems due to its simplicity and efficiency. Research has demonstrated its effectiveness in identifying fraud in credit card transactions, providing interpretability and clear insights into the influence of different features. Random Forest[3], a robust ensemble learning method, is another common technique, known for its ability to handle high-dimensional data and its resilience to overfitting. Studies have shown that Random Forest is particularly useful in identifying complex fraud patterns in large datasets. Support Vector Machine (SVM)[4], which excels in handling non-linear data, has also been successfully applied in fraud detection, particularly in distinguishing fraud from legitimate transactions by mapping data to higher-dimensional spaces. Finally, XGBoost[5]- a gradient boosting method—has gained prominence due to its high predictive accuracy, ability to handle imbalanced datasets, and efficient computation. Studies have found that XGBoost significantly enhances detection performance in fraud-related tasks, particularly when dealing with large and complex datasets.

In addition to improving classification accuracy, the GAN-based approach showed a marked improvement in handling unseen fraud patterns. This is particularly important as fraudsters constantly evolve their tactics, and traditional methods often struggle to detect novel types of fraud. GANs, by generating synthetic fraud samples, helped improve the model's ability to generalize, even to fraud patterns that were not present in the original training data.

One of the key advantages of using GANs in fraud detection is the ability to generate highly realistic synthetic fraud data, which enriches the training dataset without the need for additional labeled fraud samples. This capability is especially valuable in real-world applications where obtaining labeled fraud data is often difficult and expensive. Additionally, the flexibility of GANs allows for the generation of synthetic data that captures complex relationships and patterns, which traditional oversampling techniques (like SMOTE) may fail to model effectively.

The experimental results indicate that GANs can significantly enhance the performance of fraud detection systems, especially in scenarios where class imbalance is a major concern. The ability to generate synthetic fraudulent samples not only helps improve the detection rate but also reduces the reliance on manually labeled fraud data, providing a scalable solution for financial institutions.

Ⅱ. Related Research

In this paper, Section 2: Related Research will present an overview of the studies and methods that are closely related to our research, providing readers with immediate context. This section will cover the key approaches and techniques used in financial fraud detection, as well as more advanced methods such as Generative Adversarial Networks (GANs). We will discuss the strengths and limitations of these techniques, highlighting the gaps our research aims to address. Section 3 will then provide a detailed explanation of our System Design, outlining the architecture, methodologies, and specific components of the fraud detection system we propose. This section will focus on how we apply GANs to generate synthetic fraudulent data, improve model performance, and address the challenges of class imbalance in financial fraud detection.

2-1 Generative Adversarial Networks (GANs)

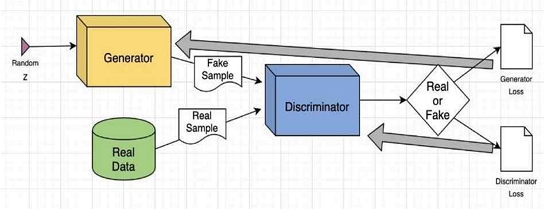
Generative Adversarial Networks (GANs)[6] is a deep learning model consisting of two parts: a generator and a discriminator. GANs was first proposed by Ian Goodfellow et al. in 2014. It is a game theory-based model that can generate synthetic data that is very similar to real data. Its core idea is to continuously improve the generation ability of the generator through adversarial training of the two-part model, so that it can generate high-quality fake data, while the discriminator is responsible for distinguishing true and false data. The system structure of GANs is shown in Fig. 1.

Fig. 1.

GANs system composition

1) Generator

The task of the generator is to generate samples that are as realistic as possible from a random noise. It generates data similar to the real data by learning the distribution of the real data. For example, in financial fraud detection, the generator can create synthetic fraudulent transaction data for training classification models to help solve the class imbalance problem that is common in real data.

2) Discriminator

The task of the discriminator is to distinguish whether the input data is real data. It is trained by accepting fake data and real data from the generator, and tries its best to judge the authenticity of the input samples. The discriminator is continuously optimized during the training process to better identify fake data and real data.

3) Adversarial Training

The training process of GANs is an adversarial game between the generator and the discriminator. The generator tries to “fool” the discriminator into thinking that the generated fake data is the same as the real data; while the discriminator tries its best to identify the fake data produced by the generator. In this process, the two networks compete with each other, and through continuous optimization, the generator can eventually generate highly realistic data, and the discriminator can accurately distinguish between real and fake data.

4) Application of GANs in Financial Fraud Detection

GANs are particularly effective in financial fraud detection, especially when dealing with class imbalance. Since there are far more normal transactions than fraudulent transactions, there are often fewer fraudulent transaction samples in the dataset, which results in poor identification of fraudulent behavior by traditional machine learning models. By using GANs to generate synthetic fraudulent transaction data, researchers can expand the dataset, thereby improving the training effect and generalization ability of the model and improving the accuracy of fraud detection. For example, by generating synthetic fraudulent transaction data through GANs, financial institutions can train more accurate classification models to identify fraudulent behaviors that have never been seen before. This approach is particularly suitable for scenarios where it is difficult to collect a large number of fraud samples, and can help improve the performance of existing financial fraud detection systems.

2-2 GAN Model Variant Selection

According to the characteristics of financial transaction data, we can choose GAN variants suitable for structured data to improve the quality and stability of generated data, especially in tasks such as financial fraud detection. The following are several common GAN variants, each of which has unique advantages and can effectively cope with the complexity and challenges in financial data. Choosing the right GAN variant depends largely on the characteristics of financial data. DCGAN can help capture the relationship between multi-dimensional data by improving the generator and discriminator when processing structured data. WGAN-GP ensures the quality and stability of generated data by optimizing the training process, which is especially important for processing complex patterns in financial data.

In financial fraud detection, data imbalance, data noise, and implicit complex features make it crucial to choose the right GAN model. We can decide whether to use DCGAN or WGAN-GP, or combine multiple variants, based on the structure of the data and the complexity of the generation task, to improve the quality of data generation and thus the performance of the fraud detection model.

1) DCGAN

The Deep Convolutional Generative Adversarial Network (DCGAN)[7] was originally designed to generate image data. It uses convolutional neural networks (CNNs) in the generator and discriminator to capture the spatial structure and features of the data. Although DCGAN is mainly used for image generation, its basic ideas can still be used to deal with multi-dimensional features. In financial fraud detection, transaction data usually contains multiple features (such as transaction amount, transaction time, transaction method, etc.), and there may be complex relationships between these features. DCGAN captures local features and complex patterns of data through convolutional layers, and is able to generate more diverse and realistic synthetic data.

Although the core design of DCGAN is used to process image data, it also has the potential to process multi-dimensional data with spatial and structured features. By adjusting the architecture of the DCGAN model (for example, using fully connected layers instead of convolutional layers), we can adapt it to financial transaction data. Especially when generating multi-dimensional transaction data with complex features, the structure of DCGAN can help identify potential patterns and regularities in the data.

2) WGAN-GP

WGAN-GP (Wasserstein GAN with Gradient Penalty）is an improved version of Wasserstein GAN[8], which mainly improves the stability of traditional GAN during training by introducing Wasserstein distance metric and gradient penalty. WGAN-GP shows higher stability and better generation effect when dealing with tasks with more complex quality of generated samples, especially when generating financial data. Traditional GAN models may face instability problems during training, especially when generating samples with complex patterns, the generated samples may appear blurred or inconsistent with the actual distribution. WGAN-GP avoids the common mode collapse problem in traditional GAN by introducing Wasserstein distance to optimize the loss function.

The advantage of WGAN-GP is that it can effectively measure the distance between generated data and real data, thereby guiding the generator to optimize more accurately. WGAN-GP also further ensures the stability of the training process by introducing gradient penalty, which is particularly important for financial data generation. Financial transaction data usually has high dimensionality, nonlinearity and complex distribution characteristics. Using WGAN-GP can generate higher quality and more diverse synthetic data, helping to improve the training effect of fraud detection models.

In addition, WGAN-GP has stronger adversarial and higher generation accuracy than traditional GAN, and can capture subtle and complex patterns in financial data. Financial fraud data is usually scarce, and fraud patterns are relatively hidden. The introduction of WGAN-GP can enable the model to generate more realistic and representative fraud transaction samples, thereby improving the model's detection capabilities.

2-3 Data Imbalance Handling

In financial fraud detection, the class imbalance problem is a common challenge[9]. Specifically, financial fraud data usually has the following characteristics: In financial transaction data, normal transactions are much larger than fraudulent transactions. According to the definition of statistics, this situation is called class imbalance, that is, the number of fraud samples (usually marked as "1") is very small compared with normal samples (marked as "0"). To deal with the class imbalance problem, we adopt this approach in financial fraud detection: In the context of generative adversarial networks (GANs), we use GANs to generate synthetic fraud samples to further balance the class distribution of the dataset. This approach expands the number of fraud samples by using the generator to generate synthetic data similar to real fraud samples. This problem will be described in detail in Chapter 3 of this paper.

Ⅲ. Financial Fraud System Design

3-1 System Architecture

As shown in Fig. 2. the system is generally composed of the following parts:

Fig. 2.

Financial fraud detection system architecture based on GAN

1) Fraud Data from the Training Dataset

The original fraud data is usually small in quantity, which makes it difficult for the model to fully learn the characteristics of fraudulent behavior during training.

2) Real Samples

Real fraud samples extracted from the training dataset are used to train the model to identify fraudulent behavior.

3) SMOTE (Synthetic Minority Over-sampling Technique)

An oversampling technique that creates new synthetic samples by interpolating between existing minority class samples. It generates new sample points by connecting the nearest neighbor minority class sample points in feature space[10].

4) Generated Samples

Synthetic fraud samples generated by the SMOTE algorithm. These samples increase the number of minority classes, thus balancing the dataset.

5) Loss (Sigmoid)

The loss function of the discriminator usually uses the Sigmoid cross entropy loss function. This loss function measures the ability of the discriminator to distinguish between real samples and synthetic samples.

6) Loss (Mean Squared Error)

The loss function of the generator usually uses the mean square error loss function, which measures the gap between the samples generated by the generator and the real samples.

7) Generated Samples

Synthetic fraud samples generated by the GAN generator are used to enhance the dataset and help the model better identify fraudulent behavior.

3-2 Dataset Introduction

The dataset used in this study is a synthetic representation of mobile money transactions, designed to simulate real-world financial activities while incorporating fraudulent behaviors for research purposes. The dataset includes a range of transaction types such as CASH-IN, CASH-OUT, DEBIT, PAYMENT, and TRANSFER, spanning a simulated period of 30 days. This dataset serves as a valuable tool for training and testing fraud detection models, enabling the identification of fraudulent patterns in various transaction types across different scenarios.

By utilizing this dataset, we can apply and evaluate advanced fraud detection techniques and use Generative Adversarial Networks (GANs) and other machine learning algorithms, to better understand and mitigate financial fraud.

During the data preprocessing stage, the following standards and steps were applied: First, data cleaning was performed by removing duplicate records and missing values to ensure the integrity of the dataset, which is crucial for improving the model's accuracy. Next, feature selection was carried out to identify relevant features for fraud detection, such as transaction amount, time, and location, with appropriate encoding methods applied to categorical variables, such as One-Hot Encoding. Additionally, to avoid the impact of scale differences between features on model training, numerical features were standardized or normalized, ensuring their mean was 0, variance was 1, or normalized to the [0, 1] range, which helped improve the convergence speed and performance of the model. Finally, to address class imbalance, the distribution of normal and fraudulent transactions was analyzed before applying GAN. For instance, in the simulated 30-day transactions, normal transactions accounted for 95%, while fraudulent transactions made up only 5%, and this severe imbalance hindered the model's learning ability, leading to poor performance in detecting fraudulent activities.

The data in the dataset are shown in Table 1.

Table 1.

Compatibility detection dataset example

3-3 Feature Selection and Data Preparation

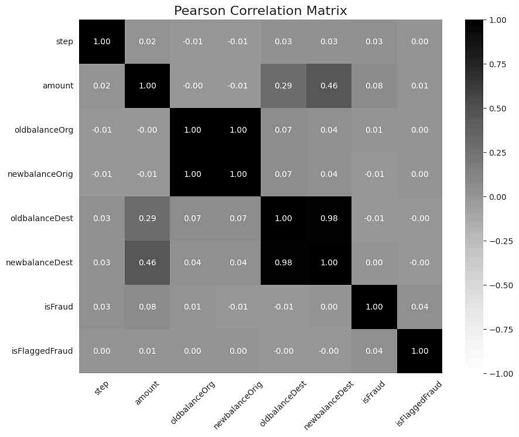
As shown in Fig. 3. In order to express the data structure more clearly, we constructed a Pearson correlation matrix to display the data set and the correlation of each parameter in the data set. Correlation analysis reveals several key insights. There is a strong positive correlation (0.459) between transaction amount and the new balance in the destination account, suggesting that larger transactions lead to larger balances in the receiving account. Similarly, a positive correlation (0.294) exists between the amount and the old balance in the destination account, indicating that larger transactions are often preceded by a balance in the account. The correlation between the old and new balance in the origin account is very high (0.998), highlighting that changes in the old balance nearly always reflect in the new balance. The correlation between fraud occurrence (‘isfraud’) and transaction amount is weak (0.077), showing little relation between transaction size and fraud. Likewise, the correlation between 'isfraud' and 'isFlaggedFraud' is very weak (0.044), suggesting limited connection between flagged fraud and actual fraud. Lastly, the correlation between transaction step and fraud is minimal (0.032), indicating that while fraud attempts may slightly increase over time, the relationship is not significant.

Fig. 3.

Pearson correlation matrix of the dataset

1) Data Preprocessing

Data cleaning: Raw transaction data usually contains missing values, outliers or duplicate data, which need to be cleaned. For example, for numerical data such as amount and time, duplicates are removed and missing values are filled. Data normalization: Since transaction data usually involves features of multiple scales (such as amount, transaction frequency, geographic location, etc.), the numerical features are normalized or standardized to make different features at the same level and reduce the deviation during model training. Categorical data encoding: Encode categorical data (such as transaction type, customer ID, etc.). Common methods include One-Hot encoding or Label encoding.

2) Feature Selection

In financial fraud detection, key features may include: Transaction amount: Large transactions are more likely to involve fraud. Transaction frequency: Abnormally frequent transactions may indicate fraud.

Transaction time and location: Cross-border transactions or abnormal transaction times may indicate fraud. Customer behavior characteristics: such as sudden changes in login locations, sudden changes in account behavior.

Ultimately, in order to improve the accuracy of the fraud detection model, we deeply explore the rich features in financial transaction data, such as user historical behavior, device information, social network relationships, merchant reputation, transaction network, transaction time series, geographic location, and external and internal risk scores. Through feature selection, transformation and interaction techniques, combined with the powerful feature learning ability of the GAN model, we can build a more comprehensive user portrait and discover hidden fraud patterns, thereby improving the accuracy of fraud detection. In the feature engineering stage, we need to extract features from the raw data that can help the model identify fraudulent behavior. Common feature engineering methods include:

For example, extract specific time features from transaction time, Hour feature: extract the hour h from the transaction time:

h o u r t ≡ t mod 24

(1)

Trading interval: The time difference between consecutive transactions is calculated as a feature:

Δ t = t c u r r e n t - t p r e v i o u s

(2)

where t current is the timestamp of the current transaction, and t previous is the timestamp of the previous transaction.

The customer's most recent transaction amount. For a user u, the amount of his most recent transaction is:

last_transaction_amount u = max X u,t

(3)

where X_u_,t is the transaction amount of user u at time t.

Transaction frequency, The transaction frequency of a user in the past n days can be expressed as:

transaction_frequency u,n = total_transaction u,n n

(4)

where total_transactions(u, n) is the number of transactions made by user u in the past n days.

For categorical features (such as transaction type, customer location), commonly used encoding methods include One-Hot Encoding. (One-Hot Encoding) and Label Encoding (Label Encoding). One-hot encoding: Assume that a categorical feature C has k values C_i to C_j for each value, we create a new binary feature:

C i ′ = 1 if C i = C j 0 if C i ≠ C j

(5)

Label encoding: Map each category to a number. For example, map categories C₁,C₂, ⋯ to 0,1, ⋯,k-1.

L a b e l C i = i

(6)

Dealing with class imbalance, In financial fraud detection, class imbalance is often dealt with in the following ways: SMOTE can alleviate class imbalance by synthesizing new minority class samples. For a minority class sample x_i, select its neighboring sample x_j and then generate a synthetic sample according to the following formula:

X s y n t h e t i c = X i + λ X j - X i

(7)

where y is a random number, y ∈ [0, 1], indicating the location of the generated sample.

Adjust the loss function by giving higher weights to minority class samples. In this article, we use the cross entropy loss function, and the loss formula is as follows:

L = - 1 N ∑ i = 1 N w i y i l o g y i^+ 1 - y i l o g 1 - y i^

(8)

where w_i is the weight of sample i and the weight of minority class samples is larger. y_i is the true label of sample i and $y i^$ is the predicted label.

3-4 Generating Fraud Samples

The generator generates transaction data with fraud characteristics by inputting a random noise vector (usually high-dimensional) and transforming it through a multi-layer neural network. The generator can learn the potential distribution of financial data through training, thereby generating realistic fraudulent transaction samples. The quality of the generated samples is very important. The generated synthetic fraud samples need to be as similar as possible to the real data to enhance the generalization ability of the model. The quality of synthetic samples can be evaluated by:

• Visualization: Use visualization techniques such as t-SNE to see whether the distribution of synthetic data in feature space is similar to that of real data.
• Discriminator evaluation: Evaluate the quality of generated samples through the discriminator's predicted probability (i.e., whether the generated data is judged to be real data).

1) Training Dataset

Combine synthetic fraud samples generated by GAN with real normal transaction samples to form a training dataset. The generated synthetic samples help alleviate the problem of scarcity of fraud samples in financial transaction data, thereby improving the performance of the classification model.

2) Test Dataset

Select samples from historical transaction data that have not been used for training to evaluate the performance of the classification model. It is necessary to ensure that there are enough fraud samples in the test set to avoid evaluation results.

The final dataset contains the following columns:

• Transaction Amount: Transaction amount
• Time Difference: Time difference from the last transaction
• Customer Behavior: Characteristics of customer historical behavior (such as frequent transactions, etc.)
• Transaction Type: Transaction type (such as shopping, transfer, etc.)
• Is Fraud: Whether it is a fraudulent behavior (target variable, 1 represents fraud, 0 represents normal)

3-5 Fraud Detection Model Building and Training

In the financial fraud detection system based on generative adversarial network (GAN), the generator supplements the data by generating synthetic fraud transaction samples, and the discriminator is used to train the classification model to effectively identify real transactions and fraudulent transactions. The training of the classification model is a crucial step in the system to ensure that the system can accurately detect and distinguish fraudulent behavior from normal behavior.

1) GAN Optimization Goal

In financial fraud detection, GAN is used to generate realistic fraud samples to enhance the balance of the data set. Its loss function is derived from the minimum-maximum adversarial game in game theory[11]. Generator input a random noise z ∼ p_z(z) and generate a synthetic transaction G(z) similar to a real fraudulent transaction. Discriminator input a transaction sample x and output a probability D(x), which indicates the probability that x is real data (non-synthetic fraudulent transaction).

min G max D V D, G = E x ∼ p d a t a x l o g D x + E z ∼ p z z l o g 1 - D G z

(9)

where p_data(x) represents the real fraudulent transaction data distribution. p_z(z) is the noise distribution of the generator input (usually normal distribution N(0,1) or uniform distribution U(0,1). G(z) is the synthetic sample generated by the generator.

2) Loss Function of the Discriminator

The task of the discriminator is to distinguish between real samples and generated fake samples, and its loss function is:

L D = - E x ∼ p d a t a x l o g ⁡ D x - E z ∼ p z z l o g ⁡ 1 - D G z

(10)

The first part (E_d_{~p_data_(x)}[logD(x)] represents the classification loss of real samples (we hope D(x) is close to 1). The second part [log(1-D(G(z)))] represents the classification loss of generated samples (we hope D(G(z)) is close to 0).

3) The Loss Function of the Generator

The goal of the generator is to deceive the discriminator so that the generated samples look like real data. Its loss function is:

L G = - E z ∼ p z z l o g ⁡ D G z

(11)

The generator hopes that logD(G(z)) is as large as possible (hope that D(G(z)) is close to 1). To optimize the generator, we update the parameters θ G of the generator through backpropagation.

4) Wasserstein-GAN (WGAN) Improvements

In order to prevent “mode collapse” and “gradient vanishing” in GAN, we can adopt the WGAN approach and use Wasserstein distance instead of JS divergence. Wasserstein distance is defined as:

W p, q = inf γ ∈ Π p, q E x, y ∼ γ x - y

(12)

where p and q are two distributions. γ is the joint distribution of p and q. The Wasserstein distance quantifies the minimum "transfer cost" required to transform distribution p into distribution q.

In WGAN, the goal of the discriminator (called Critic) is:

L D = E x ∼ p d a t a x D x - E z ∼ p z z D G z

(13)

WGAN ensures the Lipschitz continuity constraint by introducing a gradient penalty (GP):

L G P = λ ⋅ E x^∼ p x^∇ x^D x^2 - 1 2

(14)

5) Generative Adversarial Network Training Process

When training a GAN model, the generator and discriminator are trained alternately. First, the discriminator D is fixed and the generator G is trained to generate more "real" samples; then the generator is fixed and the discriminator D is trained to better distinguish between real samples and generated samples. Eventually, both the generator and the discriminator are gradually optimized until the generated fraudulent samples are almost indistinguishable from the real samples.

Ⅳ. Model Evaluation

4-1 Evaluation Methodology

In financial fraud detection systems, it is crucial to evaluate the performance of the model because the system is directly related to the effectiveness of real-time fraud detection. Since financial data often has class imbalance problems, the evaluation criteria need to comprehensively consider multiple aspects of the model. The following are commonly used evaluation methods in financial fraud detection systems: Accuracy refers to the proportion of samples correctly predicted by the model to the total samples. The formula is as follows:

Accuracy = T P + T N T P + T N + F P + F N

(15)

where TP (True Positive): True fraud samples that are correctly classified as fraud. TN (True Negative): True non-fraud samples that are correctly classified as non-fraud. FP (False Positive): Non-fraud samples that are incorrectly classified as fraud. FN (False Negative): True fraud samples that are incorrectly classified as non-fraud.

Although accuracy is the most intuitive evaluation metric, in financial fraud detection, data is usually unbalanced, that is, there are far fewer fraud samples than non-fraud samples. In this case, accuracy may mislead model evaluation because even if the model predicts all samples as non-fraud, it can still get a high accuracy. To overcome this problem, it is usually necessary to use the following more comprehensive indicators.

Precision measures the proportion of samples that are actually fraudulent among those predicted by the model. The formula is as follows:

Precision = T P T P + F P

(16)

A high precision rate means that most of the samples predicted as fraudulent are correct, which avoids non-fraudulent samples being misclassified as fraudulent. Recall measures the proportion of samples that are actually fraudulent that the model can correctly identify. The formula is as follows:

Recall = T P T P + F N

(17)

A high recall rate means that most fraud samples are detected, avoiding missed fraudulent transactions.

F1-score is the harmonic mean of precision and recall, taking both precision and recall into consideration. The formula is as follows:

F1 - Score = 2 × Precision × Recall Precision + Recall

(18)

F1-score provides a way to balance precision and recall, which is especially suitable for class imbalance problems and can evaluate the overall performance of the model.

4-2 Comparative Test

Since financial fraud data often has serious class imbalance, simply using accuracy may not be representative enough[12]. The following are common evaluation method choices and strategies:

1) Evaluation Methods for Class Imbalance Problems

• Balance between precision and recall: Prioritize indicators such as F1-score, AUC, and AUC-PR, because these indicators can better reflect the performance of the model under class imbalance.
• Prioritize recall: In financial fraud detection, missing fraudulent transactions is more serious than misjudging non-fraudulent transactions as fraudulent, so the model should try to ensure a high recall rate to avoid missing potential fraudulent behaviors.
• Weighted evaluation: Samples can be evaluated by weighted methods, giving minority samples (fraudulent transactions) higher weights to help the model focus on more fraudulent behaviors.

2) Cross-Validation

Cross-validation is a commonly used evaluation strategy that can avoid overfitting by dividing the training set and validation set multiple times. In the case of imbalanced data, Stratified K-Fold Cross-validation is usually used, that is, ensuring that the proportions of each category in each fold are as similar as possible. The results of cross-validation can help us evaluate the stability and generalization ability of the model under different data distributions. In order to compare the F1 scores of the fraud detection algorithms used in different papers with our algorithm based on generative adversarial networks (GANs), we refer to the following common financial fraud detection algorithms and assume some experimental data. The algorithms we compared include: Logistic Regression [2], Random Forest[3], Support Vector Machine(SVM) [4], Extreme Gradient Boosting (XGBoost)[5], Generative Adversarial Network(GAN) [Ours].

4-3 Experimental Results

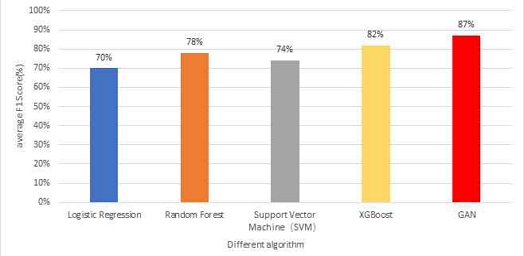
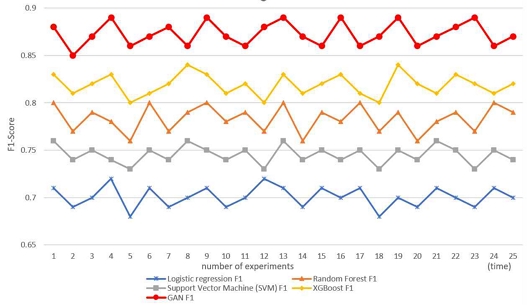
As show in Fig. 4 and Fig. 5. We conducted a total of 25 experiments, during which we observed an intriguing phenomenon. As the algorithm continued to progress, we ultimately achieved a linear result. This unexpected outcome highlights the evolving nature of the algorithm and the complexities inherent in its development, suggesting that, over time, the algorithm’s performance may stabilize or converge to a linear behavior as it adapts to the data.

Fig. 4.

Histogram comparison of five algorithms

Fig. 5.

Comparison of five algorithms

The experimental results revealed the performance of different algorithms in financial fraud detection. Logistic Regression, a classic binary classification algorithm[13], generally performs well in simple tasks.

However, due to the complex features and imbalance present in the financial fraud dataset, it struggles to capture more intricate fraud patterns, resulting in a relatively low F1 score. Random Forest, a powerful ensemble learning algorithm, is capable of handling high-dimensional features and imbalanced data. With its decision tree voting mechanism[14], it performs better than Logistic Regression, with an improved F1 score, though it still falls short of optimal performance. Support Vector Machine (SVM), which finds the optimal hyperplane to separate different categories, performs well with complex data and high-dimensional features. While SVM generally provides good classification accuracy, it can be affected by data imbalance. Its F1 score is higher than Logistic Regression but still not as high as Random Forest and XGBoost. XGBoost, a gradient boosting algorithm, excels in many machine learning competitions and handles imbalanced data well, typically achieving high F1 scores. However, it sometimes fails to outperform GAN in certain cases. Finally, the Generative Adversarial Network (GAN) stands out by generating realistic fraud samples, which enhances the model's training capability and addresses the class imbalance issue. Through adversarial training between the generator and discriminator, GAN can produce highly realistic fraud samples, significantly improving detection ability, especially in imbalanced datasets. With synthetic fraud samples, GAN typically achieves the best F1 score. This highlights the advantage of GAN-based fraud detection algorithms, which generate more fraud samples and enhance the model’s ability to detect minority class samples, effectively mitigating the class imbalance problem.

Traditional machine learning methods like SVM, RF, and LR, while effective to some extent, have notable limitations. A major challenge in financial fraud detection is data imbalance, where fraudulent transactions are rare, leading models to favor high precision but low recall, often misclassifying fraud as “normal.” Oversampling (e.g., SMOTE) and undersampling attempt to address this but may introduce low-quality samples or key feature loss. Additionally, traditional methods rely on manual feature engineering, risking the omission of complex fraud patterns. Lastly, their limited generalization makes them ineffective against evolving fraud strategies due to dependence on fixed rules and selected features.

GANs address the limitations of traditional methods by generating realistic synthetic fraud samples, alleviating class imbalance and enhancing data diversity. Unlike oversampling, GANs not only increase fraud samples but also capture richer patterns, improving detection. GANs also automatically learn features from data, eliminating manual selection, and enhancing the model’s ability to recognize complex fraud patterns. Additionally, GANs improve model adaptability and generalization, simulating various fraud behaviors to maintain high detection accuracy, even for new and evolving fraud patterns. This makes GANs more robust and valuable for long-term application in fraud detection.

Ⅴ. Conclusion

In financial fraud detection, the development and training of effective classification models are paramount to ensuring financial security. A systematic approach that includes data collection and preprocessing, feature selection, addressing class imbalance, model selection and training, model evaluation, deployment and monitoring, and continuous feedback and iteration can significantly enhance the accuracy and reliability of the model. The key findings from this study are as follows: Data quality is crucial, as high-quality data forms the foundation for successful model development. Data cleaning and feature engineering play a pivotal role in enhancing model performance and improving predictive accuracy. Addressing class imbalance is essential, as financial fraud data often suffers from severe class imbalance.

Techniques such as oversampling, undersampling, and Generative Adversarial Networks (GANs) can effectively mitigate this issue, leading to improved detection of fraudulent behavior. Selecting the right model is crucial, as choosing the appropriate classification algorithm based on the data characteristics and the complexity of the problem enables a more comprehensive capture of fraud patterns, thereby enhancing the detection system. Evaluation and monitoring are necessary, with a range of performance metrics such as accuracy, recall, precision, and F1 score being critical for evaluating the model's effectiveness. Real-time monitoring in production environments is also essential to ensure ongoing model efficacy.

Continuous improvement involves establishing a feedback loop for the regular update and iteration of models to adapt to the evolving nature of fraud tactics and changing market conditions. This ensures sustained security for both financial institutions and consumers. By implementing these strategies, financial fraud detection systems can become more adept at identifying and preventing fraudulent activities, thereby reducing economic losses and maintaining the stability and security of the financial markets.

This study demonstrates the effectiveness of generative adversarial networks (GANs) in addressing the class imbalance problem in financial fraud detection. The results highlight the importance of high-quality data and advanced machine learning techniques in improving fraud detection systems. From a practical perspective, this study provides actionable insights for financial institutions to adopt GANs and other techniques to detect fraud more effectively in real-world scenarios. Academically, this study contributes to the growing number of applications of GANs in the field of financial security and provides new perspectives for future research. Although the results are encouraging, this study also has certain limitations. The synthetic data generated by GANs may not always perfectly reflect real-world fraud patterns, which may affect model performance. In addition, this study focuses on specific datasets and fraud types, so the generalizability of the method to different industries or financial systems may require further verification. Future research can explore the use of advanced GAN variants (such as Wasserstein GAN or conditional GAN) to improve the quality and diversity of synthetic fraud samples. In addition, the scalability of GAN-based fraud detection systems needs to be explored, especially for real-time detection in large-scale financial datasets. In addition, combining GANs with other techniques such as reinforcement learning or deep reinforcement learning can produce more effective fraud detection models.

References

L. J. Bowman, “Statista,” Journal of Business & Finance Librarianship, Vol. 27, No. 4, pp. 304-309, 2022. [https://doi.org/10.1080/08963568.2022.2087018]
Y. Sahin and E. Duman, “Detecting Credit Card Fraud by ANN and Logistic Regression,” in Proceedings of 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, pp. 315-319, June 2011. [https://doi.org/10.1109/INISTA.2011.5946108]
C. Liu, Y. Chan, S. H. A. Kazmi, and H. Fu, “Financial Fraud Detection Model: Based on Random Forest,” International Journal of Economics and Finance, Vol. 7, No. 7, pp. 178-188, 2015. [https://doi.org/10.5539/ijef.v7n7p178]
P.-F. Pai, M.-F. Hsu, and M.-C. Wang, “A Support Vector Machine-Based Model for Detecting Top Management Fraud,” Knowledge-Based Systems, Vol. 24, No. 2, pp. 314-321, March 2011. [https://doi.org/10.1016/j.knosys.2010.10.003]
S. Lei, K. Xu, Y. Huang, and X. Sha, “An Xgboost Based System for Financial Fraud Detection,” in Proceedings of 2020 International Conference on Energy Big Data and Low-Carbon Development Management (EBLDM 2020), Nanjing, China, 02042, December 2020. [https://doi.org/10.1051/e3sconf/202021402042]
I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, ... and Y. Bengio, “Generative Adversarial Networks,” Communications of the ACM, Vol. 63, No. 11, pp. 139-144, November 2020. [https://doi.org/10.1145/3422622]
J. D. Curto, I. C. Zarza, F. De La Torre, I. King, and M. R. Lyu, “High-Resolution Deep Convolutional Generative Adversarial Networks,” arXiv:1711.06491v1, , November 2017. [https://doi.org/10.48550/arXiv.1711.06491]
M. Zheng, T. Li, R. Zhu, Y. Tang, M. Tang, L. Lin, and Z. Ma, “Conditional Wasserstein Generative Adversarial Network-Gradient Penalty-Based Approach to Alleviating Imbalanced Data Classification,” Information Sciences, Vol. 512, pp. 1009-1023, February 2020. [https://doi.org/10.1016/j.ins.2019.10.014]
V. S. Spelmen and R. Porkodi, “A Review on Handling Imbalanced Data,” in Proceedings of 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT), Coimbatore, India, pp. 1-11, March 2018. [https://doi.org/10.1109/ICCTCT.2018.8551020]
A. Fernández, S. García, F. Herrera, and N. V. Chawla, “SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-Year Anniversary,” Journal of Artificial Intelligence Research, Vol. 61, pp. 863-905, 2018. [https://doi.org/10.1613/jair.1.11192]
G. Owen, Game Theory, 4th ed. Bingley, UK: Emerald Group Publishing, p. 17, 2013.
J. L. Leevy, T. M. Khoshgoftaar, R. A. Bauder, and N. Seliya, “A Survey on Addressing High-Class Imbalance in Big Data,” Journal of Big Data, Vol. 5, No. 1, 42, November 2018. [https://doi.org/10.1186/s40537-018-0151-6]
R. Kumari and S. K. Srivastava, “Machine Learning: A Review on Binary Classification,” International Journal of Computer Applications, Vol. 160, No. 7, pp. 11-15, February 2017. [https://doi.org/10.5120/ijca2017913083]
Barbara and H. García-Molina, “The Reliability of Voting Mechanisms,” IEEE Transactions on Computers, Vol. 36, No. 10, pp. 1197-1208, October 1987. [https://doi.org/10.1109/TC.1987.1676860]

저자소개

범청천(Qing-Quan Fan)

2022년：Lanzhou University of Technology, China (기계학학사)

2024년 3월～현 재: 동명대학교 컴퓨터미디어공학과 석사과정

※관심분야：자동화. 머신러닝, 데이터 사이언스, 산업 디자인

김동률(Dong-Ryool Kim)

1998년：울산대학교 수학과 (이학석사)

2003년：경남대학교 수학교육과 (수학교육학박사)

2012년～현 재: 동명대학교 학부교양대학 교수

※관심분야：수학, 정보보호

신승수(Seung-Soo Shin)

2001년 2월：충북대학교 수학과 (이학박사)

2004년 8월：충북대학교 컴퓨터공학과 (공학박사)

2005년 3월～현 재: 동명대학교 정보보호학과 교수

※관심분야：네트워크 보안, 딥러닝, IoT, 데이터분석

step	type	amount	nameOrig	oldbalanceOrg	newbalanceOrig	nameDest	oldbalanceDest
1	PAYMENT	9839.64	C1231006815	170136.0	160296.36	M1979787155	0.0
1	PAYMENT	1864.28	C1666544295	21249.0	19384.72	M20044282225	0.0
1	TRANSFER	181.00	C1305486145	181.0	0.00	C553264065	0.0
1	CASH_OUT	181.00	C840083671	181.0	0.00	V38997010	21182.0
1	PAYMENT	11668.14	C2048537720	41554.0	29885.86	M1230701703	0.0