기계학습을 이용한 미세먼지 측정 음영지역의 농도 예측 연구

Ⅰ. 서 론

미세먼지는 지름 10마이크로미터 이하의 먼지를 말한다. 지름이 2.5 마이크로미터 이하인 먼지를 PM2.5라고 지름이 2.5 보다 큰 미세먼지를 PM10이라 한다. 이렇게 입자가 작은 미세먼지가 폐로 흡입되면 다양한 질병을 유발하게 된다. 미세먼지와 관련된 호흡기질환에는 만성폐쇄성폐질환, 천식, 기도염증 등의 질병들이 있다. 또한, 미세먼지는 심장순환기질환인 허혈성심장질환, 고혈압 등에도 영향을 미치는 뿐만 아니라 장기간 노출될 경우 인지능력과 기억력 감소에도 영향을 미친다[1]. 따라서 지역 주민에게 미세먼지 농도를 정확하게 예보하거나 경보발령을 통해 미세먼지에 장시간 노출을 막고 실외활동보다 실내활동을 할 수 있게 유도하거나 시민들이 마스크를 착용하고 외출할 수 있도록 안내하는 것이 중요하다.

시민의 편의를 위해서는 정확한 예보와 함께 미세먼지 측정소가 없어서 정확한 예보가 어려운 미세먼지 측정 음영지역이 최소화되어야 한다. 하지만 예산상의 문제나 측정소 설치의 어려움 때문에 미세먼지 측정소가 없는 지역이 존재하기 때문에 정확한 예보가 어려운 지역이 존재하고 있다.

또한 미세먼지 농도의 정확한 예측을 위해 대기질과 관련된 변수만 넣는 것이 아니라 기상인자도 함께 넣어 분석해야 한다. 다양한 연구에서 미세먼지 농도에 영향을 미치는 요인들을 분석한 논문에서 기상인자들이 미세먼지 농도에 영향을 미친다는 연구들이 존재한다. 박애경 외 연구에서는 미세먼지 농도에 영향을 미치는 요인 분석을 진행하였다. 분석결과 미세먼지 농도에 가장 큰 영향을 미치는 요인은 풍향과 풍속이었다[2]. 신문기 외 연구에서는 인천의 PM10 농도에 영향을 미치는 기상인자인 풍향, 풍속, 상대습도 등을 살펴보고 미세먼지로 인한 대기 오염 현상의 주요 원인 분석을 하였다. 분석결과 서풍계열 바람이 불 때 연안지역에서 발생한 오염물질이 내륙으로 수송된 영향과 대기환기량이 감소하여 오염물질 확산에 불리한 조건이 형성된 것으로 판단하였고, 미세먼지 농도는 황사 시에 가장 높았고, 강우 시에는 가장 낮은 것으로 나타났다[3]. 채희정의 연구에서는 서울 지역의 PM10 생성에 풍속과 풍향이 미치는 영향과 계절별 특성을 조사하였다. 계절과 상관없이 풍속이 강하면 PM10이 낮아지는 경향을 보였으며, 풍속은 계절별로 일정하게 영향을 미치지 않고 서풍이 강할 때 PM10이 급격히 상승하였다[4].

본 연구에서는 미세먼지 측정소가 존재하지 않는 음영지역의 농도를 예측하고자 한다. 미세먼지 측정가 많이 존재하며 유동인구가 가장 많은 서울과 경기도를 분석 지역으로 설정하였다. 예측하고자 하는 지역의 미세먼지 농도를 주변 측정소의 미세먼지 농도와 대기질 데이터, 기상관측 값인 평균기온, 일강수량, 평균풍속 데이터를 가지고 여러 모형을 설정하여 기계학습의 종류 중 다중선형회귀(Linear Regression), 서포트 벡터 머신(Support Vector Machine), 의사결정나무(Decision Tree), 랜덤포레스트(Random Forest), XGBoost, TabNet 기법을 이용하여 예측을 실시하여 예측 정확도를 평가하였다. 예측 정확도를 비교 분석하여 최적의 모형과 분석기법을 도출하고, 연구결과의 실용적 활용에 대해 제안하고자 한다.

2장에서는 미세먼지 농도 예측과 관련된 연구들을 살펴보았고, 3장에서는 연구 방법에 대한 제시하고, 4장에서는 연구방법에 따라 분석한 결과를 보여주며, 5장에서는 결론과 연구 결과의 활용방안에 대해 설명한다.

Ⅱ. 선행 연구

미세먼지 농도에 관한 연구는 수많은 문헌 연구의 주제이며, 다양한 방향의 연구가 진행되고 있다. 이러한 연구는 크게 단일 예측 모델을 적용하는 방법과 예측 성능을 향상시키기 위해 여러 방법을 결합한 하이브리드 방법으로 나뉠 수 있다.

Hu 등은 에어로졸 광학 깊이(AOD) 데이터, 기상 필드 및 토지 이용 변수를 사용하여 2011년 미국 인접 지역의 일일 24시간 평균 지상 PM2.5 농도를 추정하는 랜덤포레스트 모델을 개발하였다[5]. Maleki 등은 인공 신경망 알고리즘을 사용하여 이란(Iran)의 시간별 기준 대기 오염 물질 농도와 두 가지 대기 질 지표인 대기 질 지수(AQI)와 대기 질 건강 지수(AQHI)를 예측하였다[6]. Suleiman, Tight, & Quinn은 교통, 기상 및 오염 물질 데이터와 함께 인공 신경망, 부스트 회귀 트리(BRT, Boosted Regression Tree), 서포트 벡터 머신 등 기계학습 기반 모델을 사용하여 도로변 PM10 및 PM2.5 감축 시나리오의 효과를 평가하는 새로운 방법을 제시하였다[7]. Zhao와 Hasan은 데이터 마이닝을 사용하여 인공신경망과 서포트 벡터 머신 모델을 사용하여 홍콩 센트럴의 PM2.5 농도를 예측한 결과, 서포트 벡터 머신 모델이 인공신경망 모델보다 성능이 뛰어나다는 사실을 발견하였다[8]. 다른 연구에서는 기계학습 기법, 특히 서포트 벡터 머신과 인공신경망을 활용하여 2년 주기(2016~2018년)의 기상 및 오염 물질 파라미터를 사용하여 델리의 일일 PM2.5 농도를 예측한 결과 인공신경망 모델이 서포트 벡터 머신에 비해 예측 정확도가 더 높은 것으로 나타났다[9]. 또한 조경우 외의 연구에서도 다중선형회귀와 인공신경망을 이용하여 미세먼지 예측을 진행하였다. RMSE를 비교한 결과 다중선형회귀보다 인공신경망이 더 좋은 성능을 보였다[10].

예측을 위해 장단기 기억(LSTM)과 같은 딥러닝 모델을 사용하는 논문이 점점 더 많아지고 있다. Huang과 Kuo는 컨볼루션 신경망(CNN)과 장단기 기억(LSTM)을 결합하여 PM2.5 농도를 모니터링하고 예측하는 방법에 관해 연구하였다[11]. Yang 등은 장단기 기억과 게이트 리커런트 유닛(Gate Recurrent Unit)이라는 두 가지 딥러닝 방법의 강점을 결합한 하이브리드 모델을 제안하여 서울시 39개 측정소의 미세먼지 농도를 예측하는 데 사용하였다[12].

Park과 Chang은 인위적인 휘발성 유기 화합물에 의해 생성되는 PM2.5(미세먼지)에 대해 일정 시간 후 농도의 증가 또는 감소 여부를 예측할 수 있는 모델은 장단기 기억(LSTM) 및 인공 신경망 모델을 기반으로 시간 단위로 모델을 선택할 수 있는 알고리즘을 사용하여 개발했는데, 이는 LSTM, 인공신경망 또는 랜덤 포레스트 모델만 사용한 것보다 높은 F1 점수를 나타내었다[13].

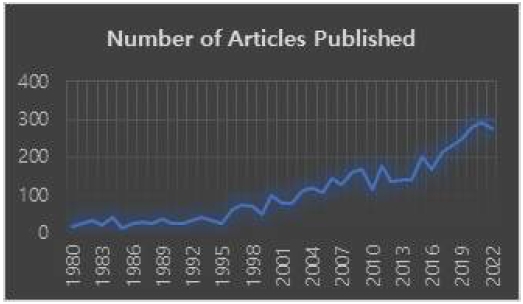
그림 1은 연도별 미세먼지 관련 논문 발표 건수의 추이를 나타낸다. 그림에서도 알 수 있듯이 논문의 수가 지속적으로 증가함을 볼 때 ESG(Environmental Social, Governance)와 건강에 대한 관심이 반영된 결과로 판단하였다.

Fig. 1.

Number of articles on particular matter by year

Ⅲ. 연구 방법

3-1 기간, 지역설정

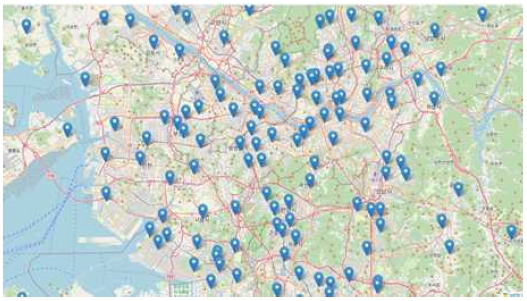
본 연구에서는 대한민국의 수도권을 중심으로 지역을 설정하였다. 수도권에 속해 있는 지역은 서울과 경기도이다. 지역을 서울과 경기도로 선정한 것은 인구가 가장 많고 충분한 미세먼지 측정소를 가지고 있는 지역이기 때문이다.

Fig. 2.

Air quality monitoring stations in Seoul and Kyung-Gi area

본 연구에 기간은 2022년 1월 2일부터 2022년 6월 15일로 설정하였다. 1월 1일부터가 아닌 1월 2일부터 기간을 설정한 것은 주변 관측소의 데이터가 같은 날에 영향을 미치는 것이 아니라 하루 전날에 데이터가 당일에 영향을 미치는 것으로 보아 1월 2일을 시작일로 설정하였다.

3-2 데이터 수집 및 전처리

1) 데이터 수집

미세먼지 농도 데이터는 환경공단에서 운영하는 에어코리아 사이트에서 오픈 API를 이용해 서울과 경기도의 미세먼지 농도 데이터를 수집하였다. 수집한 자료는 PM2.5, PM10, SO2, CO, O3, NO2의 6가지 측정값이다. 기상관측데이터와 합치기 위해 서울과 경기도의 미세먼지 측정소 정보 데이터도 수집하였다.

기상관측데이터는 시 ∙ 군 ∙구 단위의 기상관측데이터를 얻기 위해 종관기상관측데이터가 아닌 방재 기상관측데이터를 기상자료개방포털에서 CSV 파일 형태로 서울과 경기도의 데이터를 수집하였다.

방재 기상관측자료는 기상현상에 따른 자연재해를 막기 위해 실시하는 지상관측을 말한다. 관측 공백 해소 및 국지적인 기상 현상을 파악하기 위하여 전국 약 510여 지점에 자동 기상관측장비(AWS)를 설치하여 자동으로 관측한다. 서울과 경기도의 방재기상관측지점 정보 데이터도 수집하였다.

Fig. 3.

Procedure of acquiring and preprocessing the data

2) 데이터 전처리

미세먼지 농도 예측을 위해 각 미세먼지 측정소의 위도와 경도를 이용하여 가까운 5개의 측정소의 PM2.5, PM10, SO2, CO, O3, NO2의 6가지 측정값을 V1, V2, V3, V4, V5로 표시하여 변수로 나타냈다. V1이 가장 가까운 측정소를 나타낸 것이고, 주변 측정소의 6가지 측정값은 하루 전의 측정값이다. 미세먼지 측정소 정보 데이터의 주소변수에서 행정구역과 시도명을 추출하여 변수를 추가하여 미세먼지 농도 데이터와 미세먼지 측정소정보 데이터를 지점 코드를 기준으로 하나의 데이터프레임으로 합쳤다.

기상관측데이터로 사용한 평균기온, 일강수량, 평균풍속의 측정값도 하루 전의 측정값이다. 방재기상관측지점 정보 데이터의 주소변수에서 행정구역과 시도명을 추출하여 변수를 추가하여 기상관측데이터와 방재기상관측지점 정보 데이터를 지점 코드를 기준으로 하나의 데이터 프레임으로 합쳤다.

미세먼지 데이터와 기상데이터를 하나의 데이터프레임으로 합치기 전에 기상데이터에 한 지역의 기상관측지점이 여러 개 있는 경우가 있어 하나의 관측지점을 임의로 선택 후 미세먼지 데이터와 기상데이터를 합쳤다. 미세먼지 데이터와 기상데이터를 결합하였을 때 기상데이터가 존재하지 않는 경우가 있어 결합 후 결측값 제거하였다.

결측값을 제거 후 난수를 고정하여 데이터를 훈련용 데이터 세트와 테스트용 데이터 세트로 나누었다. 대부분의 기계학습 분석에서는 트레인 세트를 70~80%로 테스트 세트를 20~30%로 나누어 진행하는 것처럼 본 연구에서는 훈련용 데이터 세트를 80%로 테스트 세트를 20%를 분할하여 분석을 진행하였다.

3-3 모형 설정 및 분석 기법

미세먼지 농도를 정확하게 예측하기 위해 PM2.5와 PM10을 종속변수를 둔 모형 12가지를 만들어 기계학습에 종류인 다중회귀분석, 서포트 벡터 머신, 의사결정나무, 랜덤포레스트, XGBoost, TabNet을 사용하여 분석을 진행하였다.

다중회귀분석은 통계적 기법에서 출발하여 독립변수의 선형 결합으로 종속변수를 예측하는 모델로 그 영향 관계를 직관적으로 파악하기 용이하여 연구모델의 포함되었다.

서포트 벡터 머신은 주로 두 개의 클래스를 분류하는 데 사용되며, 데이터 포인트들 중에 두 개의 다른 범주로 나누는 최적의 경계(결정 경계 또는 초평면)를 찾는다. 서포트 벡터 머신의 핵심 아이디어는 두 범주 사이의 마진을 최대화하는 것인데 마진은 두 범주 사이의 간격을 의미하며, 이 간격을 최대화하면 새로운 데이터 포인트를 더 정확하게 분류할 수 있다. 서포트 벡터 머신은 이 최적의 마진을 찾기 위해 서포트 벡터(Support Vector)라는 데이터를 사용하는데 서포트 벡터는 결정 경계에 가장 가까운 데이터 포인트들로, 이 포인트들에 의해 경계가 결정된다. 서포트 벡터 머신은 높은 차원의 데이터를 효과적으로 처리하고, 작은 데이터 세트에서도 높은 성능을 보이는 장점이 있으나 큰 데이터 세트에서는 학습 시간이 오래 걸릴 수 있는 단점을 가지고 있다.

의사결정나무는 나무 구조로 표현되며, 각 노드는 특정한 질문이나 조건을 나타낸다. 뿌리 노드에서 시작하여, 각 질문에 따라 데이터를 분할해 나가며 가지를 뻗어나간다. 분할된 가지는 다시 다른 질문으로 세분화하는 과정을 반복하여 잎사귀 노드에 도달하게 된다. 잎사귀 노드는 최종적인 결정이나 예측 결과를 나타낸다. 의사결정나무는 직관적으로 해석하기 쉬운 장점이 있지만, 과적합(Overfitting) 문제를 일으킬 수 있어 이를 방지하기 위해 가지치기(Pruning) 등의 기법을 사용한다.

랜덤포레스트 모델은 머신러닝에서 널리 사용되는 앙상블 학습기법 중 하나입니다. 앙상블 학습은 여러 개의 기본 모델을 결합하여 최종 예측성능을 향상 시키는 방법이다. 랜덤포레스트는 이러한 앙상블 학습의 대표적인 예로, 다수의 의사결정나무를 생성하고 각 나무는 학습 데이터의 무작위 샘플링(Bootstrap Sampling)과 특정 변수의 무작위 선택(Random Subspace Method)을 통해 생성된다. 각각의 나무는 독립적으로 학습되며, 서로 다른 데이터와 변수를 사용하기 때문에 서로 다른 예측을 생성하게 되고 모든 나무의 예측 값 평균을 최종 예측 값으로 제시하는 모델이다.

XGBoost(eXtreme Gradient Boosting)는 의사결정 트리 기반의 앙상블 머신러닝 알고리즘이다. 그래디언트 부스팅의 개선된 버전으로, 이전 모델의 잔차(residual)를 보완하는 새로운 트리를 순차적으로 만들어가며 학습한다[14].

주요 특징으로는 i) L1(Lasso), L2(Ridge) 정규화를 통한 과적합 방지, ii) 자체적인 결측치 처리 방법 제공, iii) 트리 가지치기(pruning)로 모델 복잡도 제어, iv) CPU 병렬 처리 지원으로 빠른 학습 속도, v) 조기 중단(early stopping) 기능으로 효율적인 학습제공 등이 있으며 정형 데이터에서 뛰어난 성능을 보이며, 하이퍼파라미터 튜닝을 통해 다양한 문제에 적용 가능하다[15].

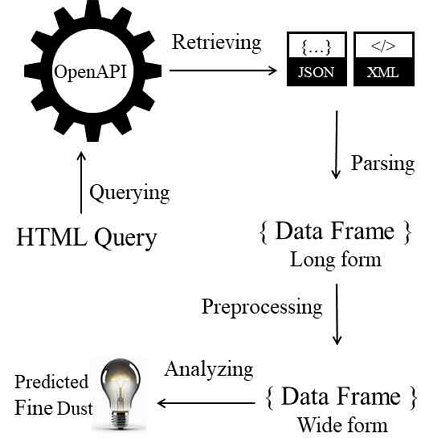
그림 4는 본 연구를 수행한 절차를 도식화한 것이다.

Fig. 4.

Research procedure

TabNet은 2021년 구글에서 발표한 정형 데이터를 위한 딥러닝 알고리즘이다[16]. 트랜스포머의 어텐션 메커니즘을 활용하여 중요한 특성을 선택적으로 학습한다. 주요 특징으로는 i) 순차적 어텐션 - 각 단계마다 다른 특성 조합에 집중, ii) 특성 선택의 해석 가능성 - 어떤 특성이 예측에 중요한지 확인 가능, iii) 자가 지도 학습 지원 - 레이블이 없는 데이터도 활용 가능, iv) 마스크 메커니즘 - 이전 단계에서 사용된 정보는 다음 단계에서 덜 중요하게 취급, v) 배치 정규화와 Sparse 정규화를 통한 과적합 방지가 가능하다.

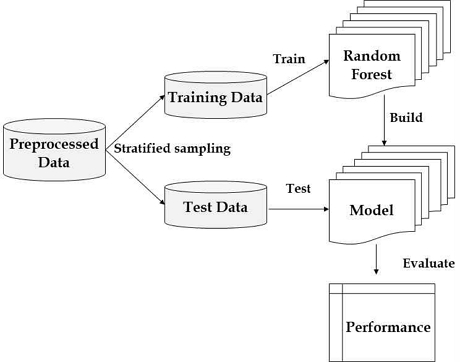
수집된 데이터를 전처리하고 기계학습에서 사용되는 샘플링 방법으로 훈련용 데이터와 테스트용 데이터로 분할한 후 훈련용 데이터를 6개의 모델로 학습시킨다. 이때 종속변수는 각각 미세먼지의 측정항목인 PM2.5와 PM10이 되며 종속변수 하나에 대해 6개의 독립변수 조합을 구성하여 72개의 모델을 형성하게 하였다. 수립된 모델은 정형데이터의 예측모형의 성능평가에 많이 사용되는 RMSE(평균제곱근오차), MSE(평균제곱오차), Adusted R2(조정된 R제곱), MAE(평균절대오차)를 측정하였다.

표 1은 종속변수가 PM 2.5로 둔 6가지 모형이다.

Table 1.

Model with PM2.5 as dependent variable

표 2는 종속변수가 PM 10으로 둔 6가지 모형이다.

Table 2.

Model with PM10 as dependent variable

다중회귀분석의 경우 독립성이 가정된다. 다중공선성을 확인하여 변수의 VIF값이 10 이상인 경우 독립성이 위반되기 때문에 VIF 값이 10 이상인 변수를 제거해야 한다. VIF 값이 10 이상인 변수를 제거하게 되면 모형의 들어가는 독립변수가 다른 5가지의 분석기법과 다르게 독립변수가 들어가게 되는 경우가 있다.

Ⅳ. 분석결과

4-1 예측성능

모델의 예측 성능을 평가하기 위한 지표로 오차 값 종류의 하나인 RMSE를 사용하였다. RMSE는 실제값과 예측값 차의 제곱합의 평균을 계산한 것으로 RMSE 식은 아래와 같다.

$\[ RMSE=\sqrt{\frac{\sum _{i=1}^n{\left(A_i-P_i\right)}^2}{n}} \]$

(1)

P_i, A_i는 각각 예측 값과 실제 값을 의미하며 n은 예측에 사용된 사례 수를 의미한다. RMSE는 실제값과 예측값의 차이인 오차가 커질수록 증가하는 지표이므로 RMSE 값이 낮은 모델일수록 좋은 예측 성능을 가진 모델이라고 할 수 있다.

Adjusted R²은 R² 값에서 조정된(Adjusted) 값으로 독립변수가 종속변수 변동을 설명하는 비율을 나타내는 통계적 지표이다. 다중선형회귀분석 모델의 정확성을 나타내는 지표로 사용된다. R² 값이 0과 1 사이의 값을 가지며 1에 가까울수록 모델이 설명하는 종속변수의 변동이 크다는 의미이나 무의미한 변수를 독립변수로 추가하여도 R² 값이 무조건 증가되는 문제를 해결하기 위해 독립변수의 개수를 고려한 지표가 Adjusted R²이다.

$\[ Adjusted R^2=1-\frac{SSR/\left(n-k-1\right)}{SST/\left(n-1\right)} \]$

(2)

MAE는 평균제곱오차를 의미하며 RMSE를 제곱한 값으로 계산된다. MAE는 평균절대오차로

$\[ MAE=\frac{\sum _{i=1}^n\left|A_i-P_i\right|}{n} \]$

(3)

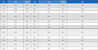
표 3은 PM2.5를 종속변수로 하고 설정된 6개 모형 - 다중회귀분석, 서포트 벡터 머신, 의사결정나무, 랜덤포레스트, XGBoost, Tabnet – 을 이용하여 예측한 결과의 성능을 나타낸 것이다.

Table 3.

PM2.5 prediction performance by model

표 3에서 가장 예측성능이 우수한 모델은 3번 데이터 세트를 사용하고 XGBoost 모델을 사용한 것으로 나타났다. 이 모델은 RMSE 값이 7.643으로 가장 낮은 것이고 동시에 Adjusted R² 값 또한 0.716으로 가장 높으며 MAE도 5.190으로 최저의 값을 가지고 있었다.

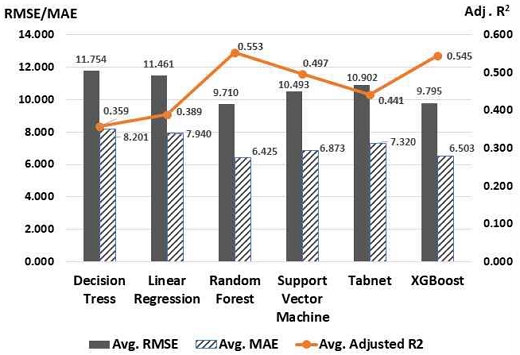
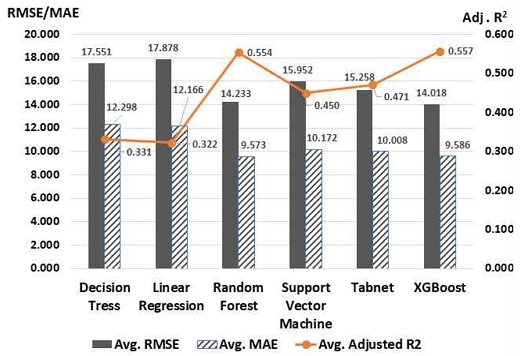
그림 5는 모형 1, 2, 3, 4, 5, 6에서 사용된 6가지 모델의 평균적인 성능을 나타낸 것이다. 분석결과로 도출된 평가지표의 값을 그래프로 표현한 것이다. 그림에서 알 수 있듯이 평균적으로는 랜덤포레스트 모델의 성능이 XGBoost보다 근소하게 우수하였으나 가장 우수한 하나의 모델을 뽑는 과정에서 XGBoost 모델이 선정되었다.

Fig. 5.

Performance comparison among models – PM2.5

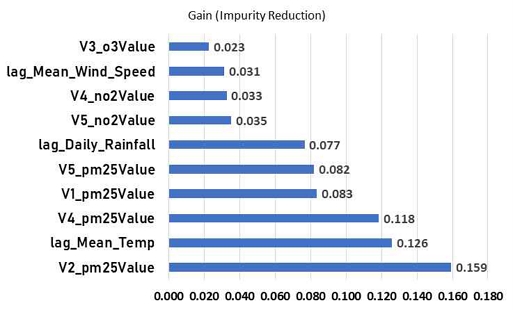
그림 6은 최적의 성능을 나타낸 XGBoost 모델에서 PM2.5 값을 예측하는데 가장 영향을 미치는 상위변수 10개를 나타낸 그래프이다. Gain은 정보이익(Information Gain)을 의미하며 특정 변수를 의사결정나무의 분할 포인트로 사용했을 때 얻을 수 있는 정보 손실 함수의 감소량을 의미한다. 이는 물리학에서 사용하는 엔트로피의 개념을 차용한 것으로 Gain이 높다는 의미는 해당 변수로 분할했을 때 모델의 성능 향상에 크게 기여하며 트리 구조에서 상위에 위치할 가능성이 높음과 동시에 예측력이 상대적으로 우수한 변수로 해석 가능함을 의미한다.

Fig. 6.

Variable importance of the best model – PM2.5

Information Gain에 가장 영향을 많이 미친 독립변수는 Station 2의 PM2.5 값(V2_pm25Value)이며 그 다음으로는 하루 전 평균기온(lag_Mean_Temp), Station 4와 Station 1의 PM2.5 값 순으로 나타났다.

PM2.5의 값을 예측하는 경우에 대체적으로 주변 Station의 하루 전날 PM2.5 농도가 중요하다는 것을 알 수 있었으며 기상 정보는 전날 평균기온과 전날 강수량이 중요한 것으로 나타났다.

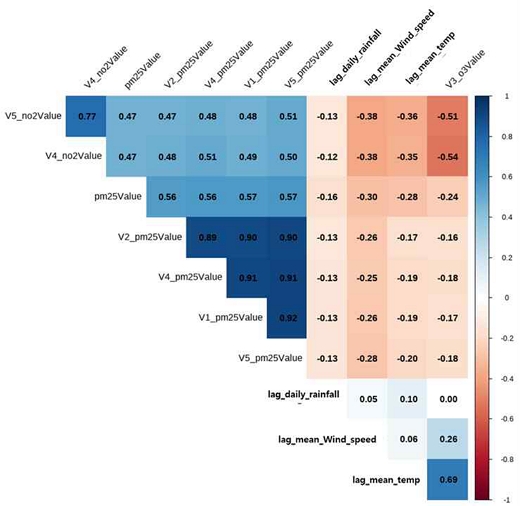
그림 7은 주요 변수 10개와 PM2.5의 상관관계를 시각화한 것으로 PM2.5는 전날 주변 Station의 PM2.5 농도가 높으면 상승하고 전날 평균기온이 높거나, 일강수량이 많거나 풍속이 높은 경우에는 내려가는 것으로 나타났다. 이는 평균기온이 높거나 풍속이 높은 경우 데워진 공기에 의해 타 지역이동이 용이하고 강수량이 높은 경우 공기 중 미세먼지가 비와 함께 지표로 떨어지기 때문으로 해석된다.

Fig. 7.

Correlation between 10 variables – PM2.5

표 4는 PM10을 종속변수로 하고 설정된 6개 모형 - 다중회귀분석, 서포트 벡터 머신, 의사결정나무, 랜덤포레스트, XGBoost, Tabnet – 을 이용하여 예측한 결과의 성능을 나타낸 것이다.

Table 4.

PM10 prediction performance by model

표 4에서 가장 예측성능이 우수한 모델은 12번 데이터 세트를 사용하고 XGBoost 모델을 사용한 것으로 나타났다. 이 모델은 RMSE 값이 10.6653으로 가장 낮은 것이고 동시에 Adjusted R² 값 또한 0.762로 가장 높으며 MAE도 7.305로 최저의 값을 가지고 있었다.

이는 PM10을 예측하는 모델에서와 동일하게 XGBoost 모델이 우수한 성능을 나타낸 것이며 상대적으로 학습하는 시간이 짧은데 비해 좋은 결과를 나타내었다.

그림 4는 모형 7, 8, 9, 10, 11, 12에서 사용된 6가지 모델의 평균적인 성능을 나타낸 것이다. 그림에서 알 수 있듯이 평균적으로는 XGBoost 모델의 성능이 우수하였으며 랜덤포레스트 모델의 성능지표보다 근소하게 우수하였다. 이는 PM2.5를 예측하는 경우 XGBoost 모델이 근소한 차이로 2위였던 것과 반대되는 상황이었다. 대체적으로 미세먼지를 예측하는데 XGBoost 모델과 랜덤포레스트모델이 좋은 성능을 나타냄을 알 수 있었다.

Fig. 8.

Performance comparison among models – PM10

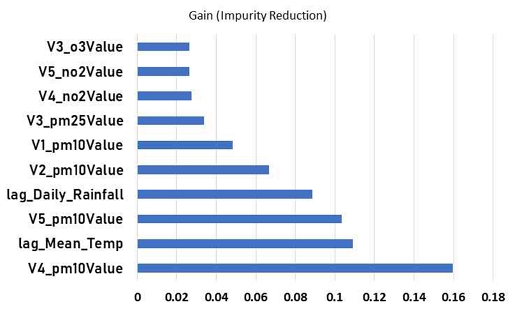
그림 9는 그림 6과 마찬가지로 최적의 성능을 나타낸 XGBoost 모델에서 PM10 값을 예측하는데 가장 영향을 미치는 상위변수 10개를 나타낸 그래프이다. 기준은 GINI를 통한 불순도 감소량을 기준으로 이용하였다. 계산한 후 변수별로 GINI 값의 감소량에 기여하는 정도가 큰 변수를 사용하였다. Information Gain에 가장 영향을 많이 미친 독립변수는 인근 Station 4의 PM10 값(V4_pm10Value)이며 그 다음으로는 하루 전 평균기온(lag_Mean_Temp), Station 5의 PM10 값(V5_pm10Value)으로 나타났다.

Fig. 9.

Variable importance of the best model – PM10

PM10의 값을 예측하는 경우에는 PM2.5의 예측과 유사하게 대체적으로 주변 Station의 하루 전날 PM10 농도가 중요하다는 것을 알 수 있었으며 기상 정보는 전날 평균기온과 전날 강수량 역시 중요한 것으로 나타났다.

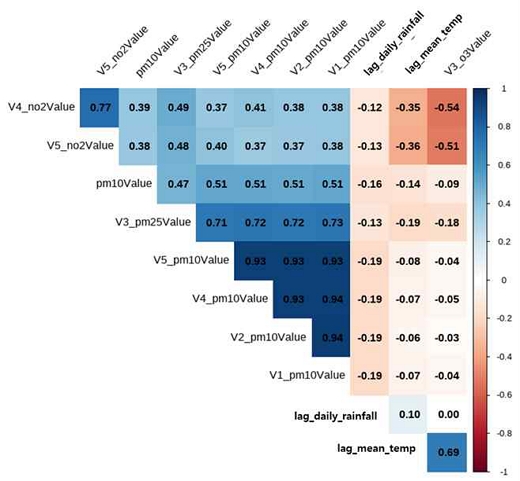
그림 10은 주요 변수 10개와 PM10의 상관관계를 시각화한 것으로 그림 7과 유사한 결과를 나타낸다. PM10은 전날 주변 Station의 PM10 농도가 높으면 상승하고 전날 평균기온이 높거나, 일강수량이 많은 경우에는 내려가는 것으로 나타났다. 이는 평균기온이 높은 경우 데워진 공기에 의해 타 지역으로 이동이 용이하고 강수량이 높은 경우 공기 중 미세먼지가 비와 함께 지표로 떨어지기 때문으로 해석할 수 있다.

Fig. 10.

Correlation between 10 variables – PM10

XGBoost가 가장 좋은 성능을 보인 것에는 Gradient Boosting의 개선된 버전이라는 점과 과적합 방지를 위한 정규화(Regularization) 기능 내장하고 다양한 손실 함수(loss function) 지원하는 특징이 반영된 결과로 판단된다.

PM2.5의 예측 성능이 좋았던 모형은 주변 미세먼지 측정소 5개의 PM25, SO(이황산가스), CO(일산화탄소), O3(오존), NO2(이산화질소)와 기상관측 변수인 평균기온, 일강수량, 평균풍속만 고려한 모형이였고, PM10의 예측 성능이 좋았던 모형은 주변 미세먼지 측정소 5개의 PM2.5, PM10, SO2(이황산가스), CO(일산화탄소), O3(오존), NO2(이산화질소)와 기상관측변수인 평균기온, 일강수량, 평균풍속을 모두 고려한 모형이었다. PM2.5와 PM10을 예측한 기계학습 분석기법에서는 XGBoost 기법이 가장 우수한 성능을 나타내었다.

Ⅴ. 결 론

미세먼지에 대한 관심이 높아지고 미세먼지가 건강에 미치는 영향이 점점 밝혀지고 있다. 그렇기 때문에 미세먼지 농도를 정확하게 예보하는 것이 중요하지만 미세먼지 측정소가 없는 지역이 존재하여 정확한 예보하는 것이 힘들다. 또한 미세먼지 농도를 시민들에게 정확하게 예보하는 것이 중요한 이유는 미세먼지는 지형과 날씨의 영향을 많이 받는다. 산간지역의 경우 비나 바람이 불지 않으면 계속 머물러 있는다. 같은 지역이라도 날씨와 지형이 다르기 때문에 측정소가 없는 음영지역의 농도 예측이 필요한 것이다. 본 연구의 목적은 미세먼지 측정소가 없는 지역인, 즉 미세먼지 음영지역의 농도를 기계학습 기법을 이용하여 예측하고자 한다. PM2.5와 PM10을 종속변수로 한 12가지 모형을 설정하였다. 12가지 모형은 주변 측정소 5개의 PM2.5, PM10, SO2, CO, O3, NO2 측정값과 기상관측 변수인 평균기온, 일강수량, 평균풍속으로 조합하여 설정하였다. 분석결과 PM2.5는 모형 3에서 PM10은 모형 12에서 분석기법인 XGBoost에서 RMSE 값과 MAE 값이 가장 낮게 나왔으며 Adjusted R² 값이 가장 높게 나와 예측 성능이 좋은 것을 확인할 수 있었다.

또한 PM2.5와 PM10의 값을 예측하는 경우 모두에서 주변 Station의 하루 전날 PM2.5 또는 PM10 농도가 중요하다며 기상 정보에서는 전날 평균기온과 전날 강수량 역시 중요한 것으로 나타났다. 이는 미세먼지 측정 음영지역의 농도예측을 위해서는 전날 주변의 미세먼지 농도와 전날 기온 및 강수량을 활용하여 예측이 가능함을 시사하고 있다.

가장 좋은 미세먼지 측정의 방법은 관측장비의 수를 음영지역에 배치하는 것이 좋겠으나 예산상의 문제나 관측장비의 설치 및 운영이 어려운 지역의 경우 본 연구의 결과를 활용하여 기계학습을 통한 간접적인 추정 방법도 활용 가능할 것으로 보인다. 또한 추가적인 활용 방안을 제안하자면 다음과 같다. 첫 번째, 미세먼지 주의보/경보 발령이다. 각 지역의 미세먼지를 정확히 예보하여 주의보/경보를 발령하여 시민들이 마스크를 쓰고 외출할 수 있게 한다. 두 번째, 살수차를 운영한다. 예측한 미세먼지 농도를 가지고 농도가 높은 지역의 경우 살수차를 운영할 수 있게 한다. 세 번째, 취약 지역 및 기관의 통보이다. 병원, 학교, 노약자 시설, 요양병원 등에 통보하여 외출을 자제할 수 있도록 활용한다. 네 번째, 웹사이트 운영이다. 미세먼지 측정 음영지역의 미세먼지 농도를 알려 줄 수 있는 사이트를 운영하여 시민들에게 보다 정확한 미세먼지 농도 정보를 제공한다.

Acknowledgments

이 논문(저서)은 2023년도 한림대학교 교비연구비(HRF-202307-001)에 의하여 연구되었음

이 논문(저서)은 2022년 대한민국 교육부와 한국연구재단의 지원을 받아 수행된 연구임(NRF-2022S1A5C2A03091539)

References

• S. Y. Kyung and S. H. Jeong, “Adverse Health Effects of Particulate Matter,” Journal of the Korean Medical Association, Vol. 60, No. 5, pp. 391-398, May 2017. [https://doi.org/10.5124/jkma.2017.60.5.391]
• A. K. Park, J. B Heo, and H. Kim, “Analyses of Factors that Affect PM₁₀ Level of Seoul Focusing on Meteorological Factors and Long Range Transferred Carbon Monooxide,” Particle and Aerosol Research, Vol. 7, No. 2, pp. 59-68, June 2011.
• M.-K. Shin, C.-D. Lee, H.-S. Ha, C.-S. Choe, and Y.-H. Kim, “The Influence of Meteorological Factors on PM10 Concentration in Incheon,” Journal of Korean Society for Atmospheric Environment, Vol. 23, No. 3, pp. 322-331, June 2007. [https://doi.org/10.5572/kosae.2007.23.3.322]
• H. Chae, “Effect on the PM10 Concentration by Wind Velocity and Wind Direction,” Journal of Environmental and Sanitary Engineering, Vol. 24, No. 3. pp. 37-54, September 2009.
• X. Hu, J. H. Belle, X. Meng, A. Wildani, L. A. Waller, M. J. Strickland, and Y. Liu, “Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach,” Environmental Science & Technology, Vol. 51, No. 12, pp. 6936-6944, June 2017. [https://doi.org/10.1021/acs.est.7b01210]
• H. Maleki, A. Sorooshian, G. Goudarzi, Z. Baboli, Y. Tahmasebi Birgani, and M. Rahmati, “Air Pollution Prediction by Using an Artificial Neural Network Model,” Clean Technologies and Environmental Policy, Vol. 21, No. 6, pp. 1341-1352, May 2019. [https://doi.org/10.1007/s10098-019-01709-w]
• A. Suleiman, M. R. Tight, and A. D. Quinn, “Applying Machine Learning Methods in Managing Urban Concentrations of Traffic-Related Particulate Matter (PM10 and PM2.5),” Atmospheric Pollution Research, Vol. 10, No. 1, pp. 134-144, January 2019. [https://doi.org/10.1016/j.apr.2018.07.001]
• Y. Zhao and Y. A. Hasan, “Machine Learning Algorithms for Predicting Roadside Fine Particulate Matter Concentration Level in Hong Kong Central,” Computational Ecology and Software, Vol. 3, No. 3, pp. 61-73, September 2013.
• A. Masood and K. Ahmad, “A Model for Particulate Matter (PM2.5) Prediction for Delhi Based on Machine Learning Approaches,” Procedia Computer Science, Vol. 167, pp. 2101-2110, 2020. [https://doi.org/10.1016/j.procs.2020.03.258]
• K.-W. Cho, Y.-J. Jung, C.-G. Kang, and C.-H. Oh, “Conformity Assessment of Machine Learning Algorithm for Particulate Matter Prediction,” Journal of the Korea Institute of Information and Communication Engineering, Vol. 23, No. 1, pp. 20-26, January 2019. [https://doi.org/10.6109/jkiice.2019.23.1.20]
• C.-J. Huang and P.-H. Kuo, “A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities,” Sensors, Vol. 18, No. 7, 2220, July 2018. [https://doi.org/10.3390/s18072220]
• G. Yang, H. M. Lee, and G. Lee, “A Hybrid Deep Learning Model to Forecast Particulate Matter Concentration Levels in Seoul, South Korea,” Atmosphere, Vol. 11, No. 4, 348, March 2020. [https://doi.org/10.3390/atmos11040348]
• J. Park and S. Chang, “A Particulate Matter Concentration Prediction Model Based on Long Short-Term Memory and an Artificial Neural Network,” International Journal of Environmental Research and Public Health, Vol. 18, No. 13, 6801, June 2021. [https://doi.org/10.3390/ijerph18136801]
• T. Chen and C. Guestrin, “XGBoost: A Scalable Tree Boosting System,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco: CA, pp. 785-794, August 2016. [https://doi.org/10.1145/2939672.2939785]
• J. Li, X. An, Q. Li, C. Wang, H. Yu, X. Zhou, and Y. Geng, “Application of XGBoost Algorithm in the Optimization of Pollutant Concentration,” Atmospheric Research, Vol. 276, 106238, October 2022. [https://doi.org/10.1016/j.atmosres.2022.106238]
• S. Ö. Arik and T. Pfister, “TabNet: Attentive Interpretable Tabular Learning,” in Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI-21), Online, pp. 6679-6687, February 2021. [https://doi.org/10.1609/aaai.v35i8.16826]