UAV 드론의 정밀 착륙 성능 향상을 위한 강화학습 기반 PID 제어기 연구
Copyright ⓒ 2024 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
도심항공교통 시스템의 핵심 요소인 무인기 드론이 도심의 목적지에 도달할 때 정밀 착륙 제어 기술은 필수이다. 특히, GPS 같은 위성 항법 시스템이 전파 방해 및 장애물로 인해 제한된 경우, 독립된 컴퓨터 비전 기반 PID 제어기를 사용해야 한다. 이때, 기존 Ziegler-Nichols 방식은 급변하는 동적 환경에 적응하기 어려워 PID 제어기 튜닝 성능을 향상하기가 어렵다. 따라서 본 논문에서는 강화학습을 이용한 PID 제어기 튜닝 방법을 제안하며 UAV 드론의 정밀 착륙 성능을 향상하고자 한다. 이를 위해, 다양한 풍속 조건에서 UAV 드론의 위치 제어 성능을 평가한 결과, 강화학습 방식은 Ziegler-Nichols 방식보다 낮은 오차율과 평균 제곱 오차 값을 기록하여 더욱 안정적인 제어 성능을 입증하였다. 본 연구를 통해 강화학습 기반 PID 제어기 튜닝 방식이 비선형 불안정 상황에서도 강인하게 작동하여 UAV 드론의 정밀 착륙 성능 향상에 기여할 것이다.
Abstract
In urban air traffic systems, precise landing control for unmanned aerial vehicles (UAVs) is critical when navigating within cities. This need becomes particularly urgent when satellite navigation systems, such as GPS, are compromised by radio interference or physical obstacles. In such cases, an independent computer vision-based proportional-integral-derivative (PID) controller must be used. However, the conventional Ziegler-Nichols method struggles to adapt to rapidly changing environments, making it challenging to optimize the tuning performance of a PID controller. This paper proposes a reinforcement learning-based method for tuning PID controllers to enhance the precision landing capabilities of UAVs. The UAV's position control performance was tested under various wind conditions, with the reinforcement learning approach achieving more stable control and lower error rates and mean square error values than the Ziegler-Nichols method. This study demonstrates that the reinforcement learning-based PID controller tuning method performs robustly in nonlinear and unstable environments, ultimately improving precision landing for UAVs.
Keywords:
UAV, Reinforcement Learning, Precision Guidance, Vision-Based, Autonomous Landing키워드:
강화학습, 정밀 유도, 비전 기반, 자동 착륙Ⅰ. 서 론
도심항공교통(UAM, Urban Air Mobility)은 도심 내 UAV(UAV, Unmanned Aerial Vehicle) 드론을 이용하여 사람이나 화물을 운송하는 항공 교통 체계로서, 조종사 없이 드론이 스스로 자율 비행하는 것이 핵심 기술이다. 특히, 도심 환경 내 목적지 도달 시 장애물 또는 빌딩풍과 같은 예상치 못한 변화를 극복할 수 있는 정밀 착륙 제어 기술이 요구되고 있다. 또한, GPS(GPS, Global Positioning System)와 같은 위성 항법 시스템은 장애물 또는 전파 방해로 사용이 불가능해질 수 있으므로, 드론에 탑재된 컴퓨터 비전 시스템을 이용한 독립적인 정밀 제어에 대한 연구가 필요하다[1].
UAV 드론은 컴퓨터 비전을 통해 착륙 지점을 인식한 후 PID(Proportional-Integral-Derivative) 제어 방식으로 드론의 자세를 조정한다. PID 제어기는 단순함과 범용성으로 인해 널리 활용되고 있으나, 고정된 환경을 기준으로 최적화되기 때문에 동적인 환경 변화에 적절하게 대응하기 어렵다는 한계가 있다[2],[3]. 특히, 도심 환경의 빌딩풍과 예측 불가능한 난류와 같은 비선형 불안정 상황에서는 PID 제어기를 제대로 조정하는 것은 어려운 문제이다[4],[5].
PID 제어기 튜닝 방법 중 널리 사용되는 지글러-니콜스(Ziegler-Nichols) 방식[6]은 시스템 반응 곡선을 기반으로 PID 제어기의 Kp, Ki, Kd 인자 값을 설정하기 때문에 비교적 단순하고 빠르다는 장점이 있다. 하지만, 고정된 시스템 모델에 의존하기 때문에 동적으로 변화하는 환경에서 효과적인 성능을 확보하는데 한계가 있다. 특히, 지글러-니콜스 방식은 불안정한 시스템 프로세스 모델에 전적으로 의존하기 때문에, 비선형 불안정 상황에서 효과적인 모델 식별이 어렵게 된다. 결국, 전체 성능이 저하되는 경우 불안정한 시스템 출력이 수렴되지 못하고 무한히 변동할 수 있다. 따라서, 복잡한 환경에 맞는 새로운 PID 제어기 튜닝 방법이 필요하다.
강화학습(Reinforcement Learning)은 지속해서 환경과 상호작용하면서 에이전트의 행동 정책을 학습하는 방식으로, 최근 UAV의 PID 제어기 튜닝에 적용되고 있다[7]-[9]. 강화학습은 학습 단계에서 환경을 랜덤하게 변화시키며 진행되기 때문에, 모델 의존도와 튜닝 민감도를 낮출 수 있다[9],[10]. 이는 다양한 외부 조건에 따라 동작 특성이 크게 변할 수 있는 UAV의 동역학적 시스템 요소를 고려할 수 있으며, 비행 중 바람의 세기나 방향이 급변할 때도 즉각적이고 유연하게 PID 제어 인자를 조정할 수 있다. 하지만, 잘못된 PID 제어기 튜닝은 성능 저하나 시스템 불안정을 초래할 수 있어서 안정적인 성능을 보장할 방법이 추가로 필요하다.
본 논문에서는 위치 오류를 직접 UAV 시스템에 전달하는 기존의 제어 방식[11]이 아닌, PID 제어기의 인자 값을 강화학습 출력값으로 설정하여 동적인 PID 제어기를 학습하는 방식을 제안한다. 이러한 접근 방식은 고전적인 PID 제어기의 안정성과 강화학습의 환경 변화 적응력을 결합함으로써 보다 향상된 제어 성능을 확보할 수 있다. 특히, PID 제어기의 인자 값을 강화학습 에이전트를 통해 동적으로 조정[12]함으로써, 시스템의 기본적인 안정성을 유지하면서 급변하는 환경에 능동적으로 대응할 수 있게 된다. 또한, 고전적인 제어 이론 기반 안정성과 신뢰성을 유지하면서도 강화학습 에이전트가 환경 변화에 적응할 수 있다. 이를 활용하며 UAV 드론의 동역학적 관점에서 다양한 환경적 변화에도 강인하게 적응할 수 있도록 PID 제어기 튜닝이 가능하다.
본 논문에서는 강화학습을 활용하여 PID 제어기 튜닝을 자동화하고, 동적인 환경에서도 UAV 정밀 착륙이 가능하게 한다. 이러한 접근법은 고전적인 PID 제어기의 안정성과 강화학습의 환경 적응력을 결합하여 향상된 제어 성능을 제공할 것으로 기대된다. 본 연구에서는 실제와 같은 다양한 풍속 조건에서 무인기 UAV 위치 제어 성능을 평가하며, Ziegler-Nichols 방식과 비교하여 제안된 강화학습 방식의 PID 제어기 튜닝의 우수성을 입증한다.
Ⅱ. 기존 PID 제어 방법
2-1 PID 제어기
UAV 드론에 활용되는 PID 제어기[13]는 비행체의 자세 제어, 고도 제어, 출력 제어 등에 널리 사용되고 있으며, 시스템의 현재 상태를 기반으로 오차값을 계산하고 이를 줄이도록 제어 출력값을 계산하는 형태로 작동된다.
| (1) |
PID 제어기는 수식 (1)과 같이 비례(Proportional), 적분(Integral), 미분(Derivative)의 세 가지 요소로 제어 값이 도출된다. MV(t)는 제어 출력 값으로, 제어 시스템에서 제어기를 통해 출력되는 값이다. Kp는 비례 항에서 사용되는 비례 상수이며, 현재 시점에서의 오차 e(t)에 비례하는 제어 신호를 생성하는데 사용된다. Ki는 적분 항에서 사용되는 적분 상수이며, 과거 오차의 누적 값을 반영하여 장기간에 거친 오차를 보정할 수 있다. Kd는 미분 항에서 사용되는 미분 상수이며 오차의 변화율을 고려하여 급격한 오차 변화에 대응한다. 기존 PID 제어 방법의 비례 항(P)은 현재 오차에 비례하여 제어 입력을 생성하며, 목표 지점(Setpoint)과의 편차를 최소화한다. 적분 항(I)은 시간에 따른 오차의 누적값을 반영하여, 지속적인 오차를 줄이고 정상 상태 오차(Steady-State Error)를 보정 하는 역할을 한다. 미분 항(D)은 현재 오차와 직전 오차를 비교하여 변화율을 계산하고, 급격한 변화에 대응할 수 있도록 제어 신호를 생성한다. 이는 시간에 따른 오차의 변화율을 미분하는 것으로, 변화의 속도를 제어하는 데 기여한다. 이러한 세 요소의 조합을 통해 PID 제어 방법은 안정적이고 신뢰성 있는 제어 성능을 제공하여 왔다.
2-2 Ziegler-Nichols PID 튜닝
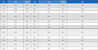
본 논문에서는 주기적 진동법을 이용한 PID 제어기 튜닝 방법인 Ziegler-Nichols[14]를 비교군으로 설정하였다. Ziegler-Nichols 방법은 정적인 환경에서 PID 제어기의 게인 값을 설정하는 고전적인 방법의 하나로서 다음 절차에 따라 작동된다. 1) 시스템에 대한 피드백 제어를 통해 비례 제어기(P-Controller)만을 사용하여 시스템을 제어한다. 2) 비례 게인(Kp)을 점진적으로 증가시켜 시스템이 안정한 한계에서 주기적인 진동을 발생하도록 한다. 3) 주기적인 진동이 발생하는 임계 게인(Ku)과 주기(Tu)를 기록한다. 4) 기록된 Ku와 Tu 값을 기반으로 PID 제어기의 각 게인을 표 1과 같이 설정한다.
Ziegler-Nichols 방법은 표 1과 같이 비교적 간단하고 빠르게 튜닝을 수행할 수 있지만, 고정된 파라미터 값만을 가지고 목표 지점에 도달하도록 제어를 진행한다. 따라서, 실제 비행 환경과 같은 비선형 불안정 상황에서 환경에 따른 유동적인 위치 제어가 불가하다는 한계가 있다.
2-3 Reinforcement Learning
강화학습[15]은 에이전트가 환경과 상호작용 하면서 주어진 환경에서 누적 보상을 최대화하도록 정책(Policy)을 학습한다. 강화학습에서는 마르코프 결정 과정(MDP, Markov Decision Process)으로 상태, 행동, 보상, 상태 전이 확률, 감각률을 정의한다. 여기서 에이전트는 현재 상태(State)를 관찰하고, 최적의 행동(Action)을 선택하며, 행동의 결과로 보상(Reward)을 받는다. 또한, 강화학습 에이전트가 탐색(exploration)과 활용(exploitation)의 균형을 맞추어가며 최적의 정책을 학습하기 때문에, 비선형 불안정 상황에서의 환경 피드백을 즉각적으로 받을 수 있어 위치 제어기 튜닝 방법으로 적합하다.
2-4 Advantage Actor-Critic (A2C) 알고리즘
Advantage Actor-Critic (A2C) 알고리즘[16]은 강화학습에서 널리 사용되는 방법의 하나로, 정책 기반 방법과 가치 기반 방법의 장점을 결합한 방식이다. A2C는 정책 함수와 가치 함수를 동시에 학습하여, 에이전트가 주어진 환경에서 최적의 행동을 선택하도록 한다. 이 알고리즘은 정책 함수의 기울기를 업데이트하는 '액터(Actor)'와 상태 가치 함수를 평가하는 ‘크리틱(Critic)’으로 구성된다. 액터는 정책 πθ(a|s)를 업데이트하여, 주어진 상태 s에서 행동 a를 선택할 확률을 출력한다. 정책은 파라미터 θ로 구성되며, 기대 보상에 대한 목적함수 J(θ)를 최대화하는 것으로 정의한다. 정책의 기울기 업데이트는 다음과 같이 이루어진다.
| (2) |
여기서 πθ(a|s)는 정책 함수이며, ∇θ는 정책 파라미터에 대한 기울기이고, A(s,a)는 어드밴티지 함수로서 특정 상태 s에서 행동 a를 취했을 때의 기대 보상이 얼마나 더 나은지를 나타낸다. 어드밴티지 함수는 다음과 같이 정의된다.
| (3) |
여기서 Q(s,a)는 행동 가치 함수로서 상태 s에서 행동 a를 취했을 때의 예상 보상을 의미하고, V(s)는 상태 가치 함수로서 상태 s에서 얻을 수 있는 예상되는 총보상을 의미한다. 이를 통해 에이전트는 주어진 상태에서 최적의 행동을 선택할 수 있도록 학습하게 된다. 크리틱은 상태 가치 함수 V(s)를 평가하는 역할을 하며, 상태 가치 함수는 다음과 같이 갱신된다.
| (4) |
여기서 α는 학습률이고 r은 현재 상태 s에서의 보상을 의미한다. 또한, γ는 할인 인자이고 s'는 다음 상태를 의미한다. 크리틱은 상태 가치 함수를 정확하게 평가 함으로써 액터가 정책을 더욱 효과적으로 업데이트할 수 있도록 유도한다. 즉, 액터는 주어진 상태에서 최적의 행동을 선택하도록 정책을 업데이트하고, 크리틱은 해당 행동의 가치를 평가하여 피드백을 제공한다. 이 과정에서 Advantage 함수를 활용하여 상태 가치 함수에서 행동 가치 함수를 빼는 방식으로 특정 행동의 상대적인 우월성을 평가한다. 이를 통해 정책 기울기 업데이트 과정에서의 분산을 줄여 더 안정적인 학습을 가능하게 한다.
Ⅲ. 강화학습 기반 PID 제어 방법
3-1 Markov Decision Process 정의
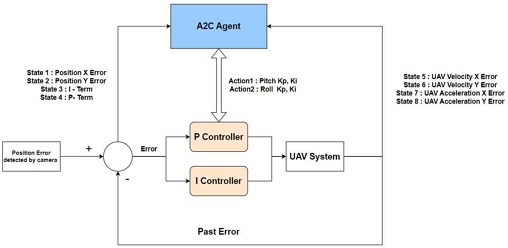
본 연구에서는 그림 1과 같이 UAV 드론의 마커 추적 문제를 마르코프 결정 과정으로 상태(State), 행동(Action), 보상(Reward)을 정의하고 각 요소는 UAV의 마커 추적 성능을 최적화하기 위해 세밀하게 설정되었다. 우선 상태(State)로는 카메라 중심과 마커의 x축 및 y축 차이, 적분 항(I-Term), 현재 오차 값(Error), 그리고 비례 항(P)을 포함하였다. 이들 상태 변수는 UAV의 현재 상태를 정확히 반영하며 마커 추적 성능을 최적화하는 데 중요한 역할을 한다. 행동(Action)으로 PID 제어기의 출력을 활용한 두 가지 제어 변수인 Pitch Output과 Roll Output을 정의하였다. Pitch Output은 UAV의 피치(Pitch) 조정을 담당하고, Roll Output은 UAV의 롤(Roll) 조정을 담당하도록 하여 UAV의 움직임을 직접적으로 제어하고 마커를 추적하도록 한다.
| (5) |
| (6) |
| (7) |
보상(Reward) 함수는 UAV의 성능을 평가하는 기준으로서 마커 추적의 효율성을 극대화하기 위한 핵심 요소이다. 수식 (5)와 같이 기본 보상으로 각 스텝 당 10점을 부여하며, 오차 변화 속도 vx,t, vy,t와 가속도 ax,t, ay,t에 따라 –10%씩 보상을 감산한다. 여기서 오차 변화 속도 vx,t, vy,t는 각 방향에서의 속도 변화율로, 현재 Step에서의 속도와 이전 Step에서의 속도 차이를 나타낸다. 가속도ax,t, ay,t는 각 방향에서 현재 Step에서의 가속도와 이전 Step에서의 가속도 차이를 의미한다. 수식 (6)에서는 오차 기반 보상 Rerror이 지수 함수로 계산된다. 오차 ex,t, ey,t는 각 방향으로 UAV과 목표 지점 간의 거리 오차를 의미한다. 오차가 작을수록 보상이 커지며, 이를 통해 목표 지점으로 유도한다. 마지막으로, 보상을 합산하여 최종 보상 Rt를 도출한다. 이러한 설계는 UAV의 급격한 기동으로 인한 비행 안정성 저하를 방지하고, 과도한 움직임을 억제하여 안정적인 비행을 유지하도록 유도한다.
오차 변화 속도와 가속도에 대한 페널티는 UAV가 목표 마커를 추적하는 과정에서 발생할 수 있는 불필요한 진동과 불안정을 줄이는 데 기여한다. 결과적으로 UAV는 더욱더 부드럽고 일관된 움직임을 유지하며 마커 추적의 정확성을 향상시킬 수 있다. 이러한 방식은 UAV가 중심점으로 정확히 정렬되도록 유도하며, 마커 추적의 효율성을 극대화하는 데 중요한 역할을 한다.
Ⅳ. 실험 및 결과
4-1 실험 목적
본 연구의 목적은 A2C 알고리즘을 활용한 자동화된 PID 제어기 튜닝 방식을 제안하며 UAV의 정밀 착륙 성능을 개선하는 것이다. UAV와 마커 간의 정렬 정확도를 평가하기 위해, A2C 알고리즘을 사용하여 PID 제어기의 파라미터를 동적으로 조정하고, UAV가 다양한 환경 조건에서도 안정적이고 정확하게 착륙할 수 있는지를 확인한다. 마커 기반 착륙 지점 인식을 통해 UAV의 정밀 착륙을 시뮬레이션하고, UAV와 마커 간의 정렬 성능을 분석하여 강화학습 기반 제어기의 효과를 검증한다. 또한, UAV가 다양한 동적 환경 변화에 어떻게 적응하는지를 분석하고, A2C 알고리즘을 통한 PID 제어기 튜닝의 적응력을 평가한다. 실시간으로 변화하는 환경 조건에서 UAV의 제어 입력 변화를 관찰하여 제어기의 안정성을 분석하고 강화학습 기반 제어기가 얼마나 효율적으로 작동하는지를 확인한다. 이러한 목표를 달성하기 위해 ROS과 Gazebo를 활용한 시뮬레이션 환경[17]을 구축하고, 다양한 시나리오에서 UAV의 착륙 성능을 실험하였다. 실험 결과를 통해 A2C 기반 PI 튜닝 방식의 실효성을 입증하고 UAV 정밀 착륙 시스템의 실용성을 제시하고자 한다.
4-2 실험 환경 구축
본 연구에서는 ROS(Robot Operating System)를 기반으로 UAV의 정밀 착륙 시스템을 테스트하기 위한 실험 환경을 구축하였다. 실험 환경은 Gazebo 시뮬레이터와 카메라 노드를 포함하여 구성되었으며, Gazebo를 활용하여 UAV의 다양한 동작과 환경 상호작용을 정확하게 모델링할 수 있는 3D 시뮬레이터를 구축하였다. 카메라 노드는 Gazebo의 카메라 플러그인을 이용해 이미지 데이터를 수집하고, 이를 ROS 네트워크를 통해 전송하는 역할을 수행한다.
실험에서는 UAV와 카메라 노드 간의 통신을 설정하여 UAV의 위치 데이터를 수집하며, Gazebo를 이용해 물리 시뮬레이션을 제공하고 UAV의 비행 및 착륙 시나리오를 모델링하였다. UAV는 시뮬레이션 된 카메라를 통해 착륙 지점을 표시하는 마커를 인식하고 위치를 조정하여 정밀 착륙을 시도한다. 이를 통해 UAV는 마커를 기준으로 착륙 지점을 탐색하고 다양한 시나리오에서 정밀한 착륙 실험을 할 수 있도록 하였다.
본 연구에서는 MAVSDK[18]를 활용하여 UAV의 비행 제어 및 정밀 착륙 시스템을 구현하였다. MAVSDK의 주요 기능으로 UAV의 이륙, 착륙, 호버링 및 경로 비행 등의 제어 명령 수행이 있으며, 이를 통해 UAV가 자동으로 특정 고도까지 이륙하거나 정해진 경로를 따라 비행할 수 있다. 이러한 기능은 UAV의 기본적인 비행 제어를 가능하게 하여 실험 목적에 맞게 드론의 동작을 쉽게 조정할 수 있게 해준다. 특히, MAVSDK를 사용하면 미리 정의된 경로를 계획하고 실행하여 드론이 자동으로 비행할 수 있다. 또한, 비행경로 계획 기능은 UAV가 복잡한 환경에서도 정확한 경로를 따라 비행할 수 있도록 하여, UAV가 목표 지점까지 최적의 경로를 따라 이동할 수 있도록 지원한다. 본 연구에서는 ROS를 통해 수집된 데이터와 MAVSDK를 통합하여 UAV의 비행 제어를 수행한다. 이를 통해 UAV가 다양한 환경 조건에서도 안정적이고 정확하게 착륙할 수 있도록 하였으며, 실험 중에는 MAVSDK를 통해 드론의 이륙과 착륙을 자동화하고, 실시간 데이터 수집 기능을 통해 드론의 상태를 지속해서 모니터링하였다.
본 연구에서는 ArUCo 마커와 포즈 추정 기술[19],[20]을 활용하였다. ArUCo 마커는 높은 인식률과 정확성을 제공하며, 다양한 조명 조건과 각도에서도 마커를 안정적으로 검출한다. 이는 UAV가 비행 중 실시간으로 착륙 지점을 정확하게 인식할 수 있어 착륙 오차를 최소화할 수 있다. 실험에서는 Gazebo 시뮬레이터 내에서 ArUCo 마커를 착륙 지점으로 설정하였으며, UAV는 시뮬레이션 된 카메라를 통해 마커를 실시간으로 인식한다. 특히, 포즈 추정 기술을 통해 UAV는 마커의 위치와 방향을 정확하게 판단할 수 있다. 이러한 위치 추정 기능 덕분에 UAV는 목표 착륙 지점을 보다 더 명확하게 판단할 수 있어 안정적인 착륙이 가능하다.
4-3 실험 조건
본 실험에서는 UAV가 마커를 효과적으로 추적하기 위해 마커의 크기를 1미터 x 1미터로 설정하고, UAV의 초기 시작 위치를 마커로부터 3미터 x 3미터 크기의 공간 내에서 무작위로 결정하였다. 이러한 설정은 UAV가 다양한 초기 조건에서 마커를 탐지하고 추적할 수 있도록 하기 위함이다. UAV의 고도는 MAVSDK를 활용하여 20미터로 설정한 후 이륙 명령을 수행하였다. 이를 통해 UAV는 일정한 고도에서 안정적으로 비행을 시작하게 되며, 마커를 탐지하고 추적할 수 있도록 하는 중요한 단계가 된다. UAV가 마커를 탐지한 후, UAV와 마커 간의 거리 차이를 계산하며, 이를 기반으로 UAV를 마커와의 거리 차가 0이 되는 지점으로 유도한다. 이러한 방식으로 각 Tuning 방법을 이용하여 거리 차를 활용한 안정도 판별을 진행하였다.
4-4 Ziegler-Nichols PID 제어기 튜닝 방법
본 연구에서는 Gazebo 시뮬레이션 환경에서 UAV 시스템의 Ku와 Tu 값을 측정하여 Ziegler-Nichols 튜닝 방식을 효과적으로 적용하는 방법을 제시한다. 실험은 먼저 Setpoint를 원점 좌표로 설정하여 UAV가 목표 지점을 향해 안정적으로 이동하도록 하였다. 이후 Kp 값을 점진적으로 증가시키면서 UAV의 반응을 관찰하였다. Kp 값을 단계적으로 증가시키는 동안 UAV의 좌표를 지속해서 모니터링하였고, UAV가 진동하기 시작하는 시점을 파악하였다. 이 시점에서의 Kp 값을 Ku로 기록하였다. Ku는 UAV 시스템이 진동을 시작할 때의 비례 게인 값으로, 지글러-니콜스 방법에서 중요한 파라미터이다. 진동이 시작된 후에는 UAV가 한 주기 동안 진동하는 데 걸리는 시간을 측정하였다. 이를 위해 UAV의 좌표 변화를 시간에 따라 기록하고, 주기적으로 반복되는 진동 패턴을 분석하였다. 이 과정을 통해 한 주기 동안의 진동 시간을 Tu로 도출하였으며, Tu는 시스템이 주기적으로 진동하는 주기를 나타내는 핵심적인 값이다. 이와 같은 실험을 통해 정확한 Ku와 Tu 값을 얻었으며, 표1의 Ziegler-Nichols 튜닝 공식을 적용하여 UAV의 PI 컨트롤러 파라미터를 설정하였다.
4-5 Reinforcement Learning PID 제어기 튜닝 방법
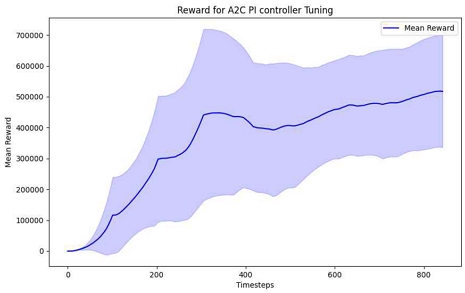
본 연구에서는 UAV 시스템의 PI 컨트롤러 튜닝을 위해 액터-크리틱(A2C) 알고리즘을 적용하여 최적의 Kp 및 Ki 파라미터를 도출하였다. UAV 드론 PX4의 매뉴얼 제어 입력 액션을 통해 피치와 롤을 효과적으로 제어하고자 하였다. 실험은 Gazebo 시뮬레이션 환경에서 수행되었으며, 이는 실제 PX4 펌웨어의 동작 조건을 세밀하게 반영하도록 설정되었다. 강화학습 에이전트는 A2C 알고리즘을 사용하여 PI 컨트롤러의 Kp와 Ki 파라미터를 결정하도록 훈련되었고, UAV의 성능에 따라 보상을 받는 방식으로 학습이 진행되었다. Gazebo 환경은 UAV의 실제 동역학과 제약 조건을 재현하여 높은 정확도로 훈련이 가능하게 하였다. 학습 과정은 40 에피소드로 구성된 세트를 10번 반복하는 것으로 이루어졌으며, 각 반복에서 UAV는 40개의 에피소드를 수행하며 PI 컨트롤러의 파라미터를 조정하였다. A2C 알고리즘은 UAV의 성능을 평가하고 보상을 부여하며, 이를 기반으로 파라미터를 업데이트하였다. 또한, UAV가 다양한 초기 조건을 경험할 수 있도록 매 에피소드 시작 시 ±3m 범위에서 랜덤하게 배치하는 방식을 채택하였다. 이러한 접근은 UAV가 다양한 위치와 상황에서 안정적으로 학습할 수 있게 하여 모델의 강인성을 크게 향상했으며, 학습된 모델이 실제 환경에서도 일관된 성능을 유지할 수 있도록 하였다.
4-6 연구 결과 비교
본 연구에서는 표2와 표3에서와 같이 UAV의 위치 제어 성능이 다양한 풍속 조건에서 강화학습 방식이 지글러-니콜스(Ziegler-Nichols: Zieg) 방식보다 우수하다는 것을, 실험을 통해 확인하였다. UAV는 설정된 목표 지점에서 안정적으로 위치를 유지하였으며, UAV의 제어 성능을 정량적으로 분석하였다.
첫째, UAV와 마커 간의 탐지 가능한 거리인 ±300cm 내에서, UAV의 위치는 실시간으로 Pose estimation을 통해 측정되었다. 측정된 거리는 목표 지점(0cm)에서의 벗어남을 백분율로 환산하여, UAV의 위치 안정성을 평가하는 데 기여하였다. Root Mean Square (RMS) 값을 사용하여 UAV의 위치 안정성을 수치화하였으며, RMS 값이 낮을수록 UAV의 위치가 안정적임을 나타내었다.
둘째, 각 실험은 300초 동안 5회 반복하며, 각 반복에서 측정된 백분율 값과 RMS 값을 기록하였다. 5번의 반복 실험에서 도출된 평균값은 UAV의 목표 지점에서의 벗어남 정도와 위치 안정성을 종합적으로 평가하는 데 사용되었다. 실험 결과는 UAV가 다양한 풍속 조건에서도 목표 지점을 얼마나 정확하게 유지할 수 있는지를 보여주었으며, 평균 백분율 값과 RMS 값을 통해 UAV의 위치 제어 성능을 정량적으로 평가하였다.
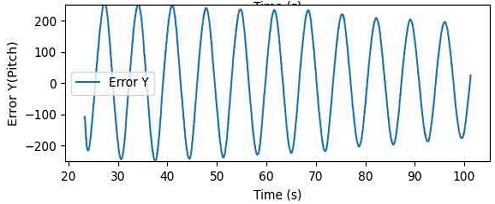
셋째, Cross Wind와 Head Wind 환경에서 RL 방식과 Ziegler-Nichols 튜닝 방식을 비교한 결과, Cross Wind 환경에서는 RL 방식이 Ziegler-Nichols 방식보다 전 구간에서 낮은 오차율과 RMS 값을 기록하여 더욱 우수한 성능을 나타냈다. Head Wind 환경에서도 RL 방식은 대부분 구간에서 더 낮은 오차율과 RMS 값을 보였으며, 이는 Ziegler-Nichols 방식보다 안정적인 제어 성능을 입증하였다.
Ⅴ. 결 론
본 논문에서는 UAV 드론의 정밀 착륙 성능 향상을 위한 강화학습 기반 PID 제어기 튜닝 방식을 제안하였다. UAV가 독립된 컴퓨터 비전 기반으로 정밀 착륙을 수행해야 하는 상황에서 PID 제어기 튜닝 방식에 따른 위치 제어 성능을 다양한 풍속 조건에서 평가하였다. 결과적으로 강화학습 방식이 Ziegler-Nichols 방식에 비해 우수한 성능을 보였으며, Cross Wind와 Head Wind 환경에서 RL 방식은 Ziegler-Nichols 방식보다 낮은 오차율과 RMS 값을 기록하여 더욱 안정적인 제어 성능을 확인하였다. 강화학습 특성상 학습된 정책에서 미세한 오차 및 진동 특성이 발생할 수 있으므로, 향후 연구에서는 제어기의 안정성에 초점을 맞춤 강화학습 알고리즘으로 개선하고자 한다. 또한, 실세계 환경에서 다양한 환경 변화에서 UAV 드론의 정밀 착륙 제어기의 강인성을 확보하기 위해 추가 연구를 진행하고자 한다.
Acknowledgments
이 논문은 동아대학교 교내연구비 지원에 의하여 연구되었음.
References
-
Y. Rao, S. Ma, J. Xing, H. Zhang, and X. Ma, “Real Time Vision-Based Autonomous Precision Landing System for UAV Airborne Processor,” in Proceedings of 2020 Chinese Automation Congress (CAC), Shanghai, China, pp. 532-537, November 2020.
[https://doi.org/10.1109/CAC51589.2020.9326776]

-
M. Yuan, C. Wang, P. Zhang, and C. Wei, “PID with Deep Reinforcement Learning and Heuristic Rules for Autonomous UAV Landing,” in Proceedings of 2022 International Conference on Autonomous Unmanned Systems (ICAUS 2022), Xi’an, China, pp. 1876-1884, September 2022.
[https://doi.org/10.1007/978-981-99-0479-2_174]

-
X. Yu, L. Yan, Z. Guan, Y. Wu, F. Peng, and F. Yan, “Control of Fixed-Wing UAV Using Optimized PID Controller with the Adaptive Genetic Algorithm,” in Proceedings of 2022 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Guiyang, China, pp. 298-303, July 2022.
[https://doi.org/10.1109/RCAR54675.2022.9872224]

-
M. A. Sadi, J. Annisa, and A. M. N. A. Kamaruddin, “Enhancing Quadrotor UAV Efficiency Amidst Turbulent Winds in Mangrove Area: A Hybrid PID-Grey Wolf Optimizer Control Approach,” in Proceedings of 2023 IEEE 9th International Conference on Smart Instrumentation, Measurement and Applications (ICSIMA), Kuala Lumpur, Malaysia, pp. 159-164, October 2023.
[https://doi.org/10.1109/ICSIMA59853.2023.10373472]

-
T. Shuprajhaa, S. K. Sujit, and K. Srinivasan, “Reinforcement Learning Based Adaptive PID Controller Design for Control of Linear/Nonlinear Unstable Processes,” Applied Soft Computing, Vol. 128, 109450, October 2022.
[https://doi.org/10.1016/j.asoc.2022.109450]

-
S. Singh, V. Singh, A. Rani, and J. Yadav, “Optimization of PID Controller Based on Various Tuning Methods,” in Proceedings of 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, pp. 1-6, February 2023.
[https://doi.org/10.1109/PIECON56912.2023.10085805]

-
X. J. Blake and N. Aphiratsakun, “Reinforcement Learning for PID Gain Tuning in Ball-and-Beam Systems: A Comparative Study,” in Proceedings of the 1st International Conference on Robotics, Engineering, Science, and Technology (RESTCON), Pattaya, Thailand, pp. 187-190, February 2024.
[https://doi.org/10.1109/RESTCON60981.2024.10463594]

-
K. B. Trujillo, J. G. Álvarez, and E. Cortés, “PI and PID Controller Tuning with Deep Reinforcement Learning,” in Proceedings of 2022 IEEE International Conference on Automation/XXV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Curicó, Chile, pp. 1-6, October 2022.
[https://doi.org/10.1109/ICA-ACCA56767.2022.10006166]

-
S. Sonmez, S. Martini, M. J. Rutherford, and K. P. Valavanis, “Reinforcement Learning Based PID Parameter Tuning and Estimation for Multirotor UAVs,” in Proceedings of 2024 International Conference on Unmanned Aircraft Systems (ICUAS), Chania, Greece, pp. 1224-1231, June 2024.
[https://doi.org/10.1109/ICUAS60882.2024.10557032]

-
Y. Zhen, M. Hao, and W. Sun, “Deep Reinforcement Learning Attitude Control of Fixed-Wing UAVs,” in Proceedings of the 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, pp. 239-244, November 2020.
[https://doi.org/10.1109/ICUS50048.2020.9274875]

-
K. Dergachov, S. Bahinskii, and I. Piavka, “The Algorithm of UAV Automatic Landing System Using Computer Vision,” in Proceedings of 2020 IEEE 11th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, pp. 247-252, May 2020.
[https://doi.org/10.1109/DESSERT50317.2020.9124998]

-
X. Yu, W. Hu, J. Quan, and R. Wang, “Research on the Optimization of Flight Control Technology for UAVs Based on Reinforcement Learning on Moving Platform,” in Proceedings of the 4th International Conference on Computers and Artificial Intelligence Technology (CAIT), Macao, pp. 200-205, December 2023.
[https://doi.org/10.1109/CAIT59945.2023.10468874]

-
K. H. Ang, G. Chong, and Y. Li, “PID Control System Analysis, Design, and Technology,” IEEE Transactions on Control Systems Technology, Vol. 13, No. 4, pp. 559-576, July 2005.
[https://doi.org/10.1109/TCST.2005.847331]

-
J. C. Basilio and S. R. Matos, “Design of PI and PID Controllers with Transient Performance Specification,” IEEE Transactions on Education, Vol. 45, No. 4, pp. 364-370, November 2002.
[https://doi.org/10.1109/TE.2002.804399]

-
M. Kaloev and G. Krastev, “Experiments Focused on Exploration in Deep Reinforcement Learning,” in Proceedings of the 5th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, pp. 351-355, October 2021.
[https://doi.org/10.1109/ISMSIT52890.2021.9604690]

-
H. Cui, D. Wang, Q. Li, X. Liu, and H. Lu, “A2C Deep Reinforcement Learning-Based MEC Network for Offloading and Resource Allocation,” in Proceedings of the 7th International Conference on Computer and Communications (ICCC), Chengdu, China, pp. 1905-1909, December 2021.
[https://doi.org/10.1109/ICCC54389.2021.9674631]

-
J. García and J. M. Molina, “Simulation in Real Conditions of Navigation and Obstacle Avoidance with PX4/Gazebo Platform,” in Proceedings of 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kyoto, Japan, pp. 979-984, March 2019.
[https://doi.org/10.1109/PERCOMW.2019.8730764]

- MAVSDK. Python·MAVSDK Guide [Internet]. Available: https://mavsdk.mavlink.io/main/en/python/, .
-
R. Wang, H. Guo, X. Wang, and L. Han, “The Effect of ArUco Marker Size, Number, and Distribution on the Localization Performance of Fixed-Point Targets,” in Proceedings of the 6th International Conference on Robotics, Control and Automation Engineering (RCAE), Suzhou, China, pp. 118-123, November 2023.
[https://doi.org/10.1109/RCAE59706.2023.10398770]

-
A. Marut, K. Wojtowicz, and K. Falkowski, “ArUco Markers Pose Estimation in UAV Landing Aid System,” in Proceedings of 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Turin, Italy, pp. 261-266, June 2019.
[https://doi.org/10.1109/MetroAeroSpace.2019.8869572]

저자소개

2024년 7월~2024년 8월: ㈜쿼터니언 학부생 인턴
2019년~현 재: 동아대학교 전자공학과 학사과정
※관심분야 : UAV, 강화학습, 정밀 유도, 인공지능

2001년:동아대학교 전자공학과(공학학사)
2005년:한국과학기술원 대학원(공학석사)
2014년:한국과학기술원 대학원(공학박사)
2001년~2003년 삼성전자 연구원
2005년~2009년: LG전자 선임연구원
2011년~2022년: 한국전자통신연구원 책임연구원
2022년~현 재: 동아대학교 컴퓨터‧AI공학부 조교수
※관심분야:강화학습, 로봇, 인공지능, 군집지능