에이다부스트에서 약한 학습기로 사용하는 결정트리 알고리즘들의 비교: CART, LDA

Ⅰ. 서 론

앙상블(ensemble) 학습은 여러 분류기의 결과를 투표(vote)하여 최종결정하는 것으로 배깅과 부스팅 기법으로 크게 나누어진다. 배깅의 경우 학습 데이터에 샘플링을 다르게 하여 여러 개의 학습 집합으로 나눈 다음, 각각의 학습 집합을 별도의 분류기 모델에 할당하고 학습한다. 그리고 테스트 데이터를 이 모델들에 입력하면 여러 개의 예측 결과가 나오는데, 이들에 투표기법의 다수결을 이용해 최종 결과를 얻는다. 따라서 이 방법은 과적합(overfit)으로 인해 낮은 편기(bias)와 높은 분산(variance)의 특징을 가지며, 각 모델에서 샘플링과 학습을 하는 과정은 모델마다 서로 독립이므로 병렬로 수행할 수 있다. 반면 부스팅은[1],[2] 학습 데이터에 약한 학습기로 학습하여 예측이 틀리는 사건에 대해 샘플링 가중치를 높임으로써 다음 학습기에 학습 데이터로 선택될 확률을 높이는 과정을 여러 번 반복하여 사건들을 정확하게 분류하도록 기회를 주는 것이다. 최종 결과는 학습 결과에 가중치를 반영하는 투표를 통해 결정한다. 따라서 이 방법은 분류기의 성능이 0.5보다 약간 좋은 약한 분류기를 사용하는 과소적합(underfit)으로 인해 높은 편기와 낮은 분산의 특징을 가진다. 또한 다수의 분류가 순차적으로 샘플링과 학습을 반복하며 약한 학습기에서 강한 학습기로 변화해 간다.

결정트리는 수치와 범주형 데이터 모두에 적용하여 데이터 특성을 결정 규칙으로 분류하며 트리 형식으로 나타낸다. 이는 데이터를 시각화해 주어 해석을 쉽게 할 수 있는 장점이 있어 분류와 회귀 분야에 전통적으로 사용되어 오고 있다. 여러 결정트리는 근사 최적의 분류 방법에 따라 구분되며, 정보 이득(IG) 함수로 이를 표현하게 된다. 기존의 알고리즘들의 IG 함수들은 엔트로피, 지니 인덱스, 고유 벡터, 고유값 등을 조합하여 목적을 달성하려 했다. 따라서 결정트리에서 가장 중요한 부분은 IG 함수를 고안하는 것이고, 이 IG 함수의 목표는 근사 최적의 분류면을 구하여 트리의 노드에 표현하는 작업을 반복하여 되도록 작은 트리로 전체 규칙 정보를 대표할 수 있도록 하는 것이다[1],[2].

에이다부스트는 목적지에 빠르게 수렴하고 가설(모델)의 개수인 라운드 수를 제외하고 별도의 매개변수가 필요 없다는 점, 다양한 분류 알고리즘을 약한 분류기로 사용할 수 있다는 장점이 있다. 이에 따라 본 논문은 부스팅 기법의 일종인 에이다부스트에 대해 이론적인 배경과 함께 알고리즘의 발전 과정을 알아본다. 그리고 에이다부스트에서 핵심인 결정트리를 바탕으로 약한 분류기를 구성하는 두 가지 방법인 선형 판별 분석(Linear Discriminant Analysis, LDA) 알고리즘[3],[4]과 CART(Classification And Regression Tree) 알고리즘[5]-[8]을 소개하고 서로의 성능을 비교하여 각각의 차이점에 대해 알아본다. LDA는 Fisher의 선형판별함수를 기반으로 데이터의 특성을 가장 잘 표현하는 속성의 선형조합을 구한다는 점에서 주성분 분석(Principal Component Analysis, PCA)과 유사한 점이 있으며, 부류 간의 관계를 고려하느냐에 따라 차이점을 구분한다. 이러한 LDA는 차원 축소 방법을 사용하며 여러 응용에 사용되어 좋은 결과를 보여왔다. 그리고 CART 방법은 최근에 소개된 앙상블 알고리즘에서 가장 널리 사용되고 있다는 점에서 비교 대상으로 선택하였다.

2장에서는 에이다부스트의 핵심 요소인 약한 분류기를 구성하는 CART와 LDA로 결정트리의 학습 알고리즘을 설명한다. 3장에서는 2장에서 소개된 2가지 약한 분류기를 적용하는 에이다부스트를 소개하고 이론적인 배경을 소개한다. 그리고 이진 분류기에서 다중 분류기로 발전하는 과정을 정리한다. 4장은 이들 2가지 약한 분류기를 에이다부스트 알고리즘에 적용한 결과를 여러 학습 데이터의 실험을 통해 비교해 본다.

Ⅱ. 배 경

결정트리는 계층적 구조, 분할, 학습, 그리고 예측 기준에 따라 종류를 분류하며, 시각적인 해석을 쉽게 한다는 특징을 가진다. 또한 결정트리는 과적합의 가능성 때문에 절단(pruning)이나 앙상블 기법과 결합하여 사용한다.

이 장에서는 결정트리를 구성하는 CART와 LDA의 배경 이론을 설명하여 앙상블의 약한 분류기로 사용되는 과정으로 연결되도록 한다.

2-1 CART 결정트리

CART[5]는 Random Forest[9], GBM[10], XGBoost[8], LGBM[11]과 같은 앙상블 알고리즘에서 결정트리를 위한 기본 모델로 사용된다는 점에서 중요도를 가진다. 그리고 CART는 명목 범주형(nominal categorical) 데이터 보다는 순서가 있는 연속 수치형(continuous numerical) 데이터를 처리하기에 적합한 것으로 알려져 있다. 이는 명목 범주형 데이터가 레이블링(labeling) 과정에서 원-핫 인코딩(one hot encoding)을 사용함으로 인해, 결정트리를 깊은 편향(skewed) 이진 트리 형태로 만들어, 절단 과정을 거치고 나면 성능 저하로 이어지게 하는 경향이 있기 때문이다. 특히 앙상블 모델에서는 약한 분류기를 사용하는데 이때 전체 성능에 영향을 미치게 된다.

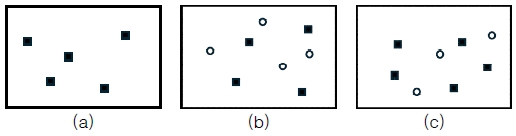
CART 알고리즘은 혼란(impurity)의 정도를 정의하면서 출발하는데 혼란 정도를 측정하기 위하여 식 (1)과 같은 C4.5에서의 엔트로피(entropy)와 CART에서의 지니 인덱스(gini index)가 가장 널리 사용된다. 여기서 c는 부류 수, m은 임의의 노드에서 전체 사건의 수를 의미한다. 엔트로피와 지니 인덱스를 설명하기 위해 그림 1과 같은 예로 식 (1)의 계산 과정을 설명한다.

$\[ \begin{array}{c}\text{Entropy} H\left(m\right)=-\sum _{i=1}^{c}p\left(i|m\right)\cdot {\text{log}}_{\text{2}}p\left(i|m\right)\hfill \\ \text{GiniIndex }G\left(m\right)=1-\sum _{i=1}^{c}p{\left(i|m\right)}^2\hfill \end{array} \]$

(1)

Fig. 1.

Examples of events at random nodes

그림 1의 (a)에서는 하나의 부류만으로 구성되어 가장 낮은 혼란도(0)를 가지며 엔트로피와 지니 인덱스 모두가 0의 값을 가진다.

$\[ H\left(t\right)=-\left(\frac{5}{5}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{5}{5}+\frac{0}{5}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{0}{5}\right)=0, \]$

$\[ G\left(t\right)=1-\left({\left(\frac{5}{5}\right)}^2+{\left(\frac{0}{5}\right)}^2\right)=0 \]$

다음으로, 그림 1의 (b)는 가장 높은 혼란도를 가진다. 여기서, 2개의 부류일 때 가장 높은 엔트로피인 1을, 지니 인덱스에서 가장 높은 값인 0.5를 가지게 된다.

$\[ H\left(t\right)=-\left(\frac{4}{8}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{4}{8}+\frac{4}{8}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{4}{8}\right)=1.0 \]$

$\[ G\left(t\right)=1-\left({\left(\frac{4}{8}\right)}^2+{\left(\frac{4}{8}\right)}^2\right)=0.5 \]$

마지막으로, 그림 1의 (c)는 다음과 같이 혼란도를 계산할 수 있다.

$\[ H\left(t\right)=-\left(\frac{5}{8}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{5}{8}+\frac{3}{8}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{3}{8}\right)=0.95 \]$

$\[ G\left(t\right)=1-\left({\left(\frac{5}{8}\right)}^2+{\left(\frac{3}{8}\right)}^2\right)=0.47 \]$

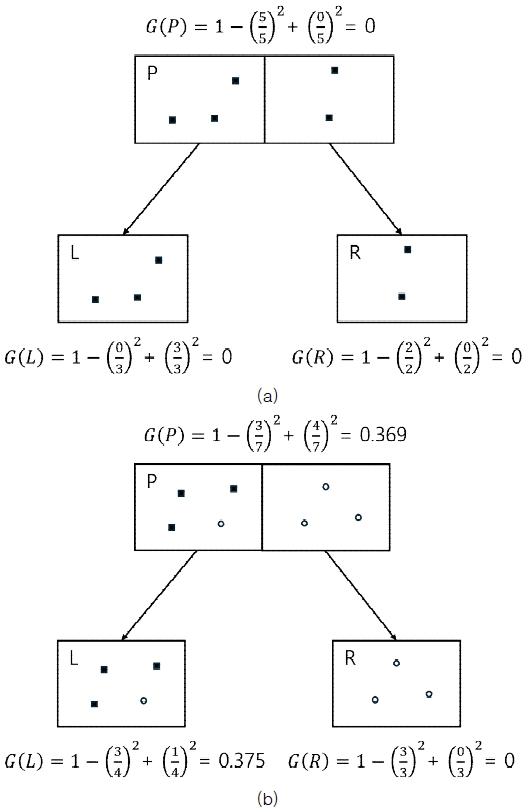
CART에서는 이와 같은 혼란도를 이용해 식 (2)와 같은 정보 이득(Information Gain, IG) 함수를 구하게 되는데, 이는 루트 노드가 왼/오른쪽 노드로 분리될 때 혼란도의 변화량을 의미한다. CART 결정트리 알고리즘은 가장 커다란 IG로 트리를 구성해 나가는 과정이다. 이와 관련해서 그림 2와 같은 예를 들 수 있다. 여기서 P: 부모, L: 왼쪽, R:오른쪽이다.

$\[ IG=G\left(P\right)-\frac{m_L}{m}\times G\left(L\right)-\frac{m_R}{m}\times G\left(R\right) \]$

(2)

Fig. 2.

Example of information gain (IG) in a decision tree

그림 2의 (a)를 식 (2)에 적용하면, 정보 이득 함수는 $$ IG=0-\frac{3}{5}\times 0-\frac{2}{5}\times 0=0$$이고, (b)에서 정보 이득 함수는 $$ IG=0.369-\frac{4}{7}\times 0.375-\frac{3}{7}\times 0=0.155$$이다. 따라서 ((a)의 IG < (b)의 IG))이므로 CART의 임의 노드에서는 (b)를 선택하여 결정트리를 구성하게 된다.

Ⅲ. CART와 LDA 결정트리를 약한 학습기로 사용하는 에이다부스트

3-1 에이다부스트

Yoav Freund[1]는 약한 학습모델을 점진적으로 강하게 하여 강한 학습기로 만들어 가는 에이다부스트 알고리즘을 제안하였다. 이는 학습모델에서 오 분류된 사건의 가중치를 높임으로써 이 사건이 다음 모델의 학습 데이터에 포함되도록 샘플링 확률을 높인다. 그리고 정해진 횟수만큼 이 과정을 직렬방식으로 반복하여 정확도가 증가하도록 한다. 입력 사건에 대한 부류는 마지막 추정 과정에서 여러 모델의 결과들을 결합하여 결정한다. 이러한 학습과 추정 과정을 자세히 살펴보면 다음과 같다. 여기서 학습 데이터는 m개(i=1,⋯,m)이며 속성 벡터는 k개(x₁,...,x_k)이고 부류 값은 y={+1, -1}로 정한다.

먼저 일양 분포에 따르는 가중치(D) 확률과 복원 추출 방법으로 학습 사건들에서 정해진 수만큼(m개) 샘플링 한다.

$\[ D_1\left(i\right)=1/m \]$

결정트리, SVM, LDA 등의 분류 알고리즘을 절단 등의 방법으로 정확도가 0.5보다 약간 우수한 정도의 약한 학습기를 구성하고 이를 모델로 만든 후, 샘플된 데이터를 이 모델(h)로 학습하여 각각 추정치($$ \widehat{y}=h_1\left(x_i\right)$$)를 구한다.

분류된 결과($$ \widehat{y}$$)에 따라 식 (7), (8), (9)의 순서대로, 다음 모델에 입력 데이터를 선택하기 위한 가중치를 구한다.

$\[ {\epsilon }_1=\sum _{i=1}^m{D}_1\left(i\right)I\left(y_i\ne \widehat{y_i}\right) \]$

(7)

$\[ {\alpha }_1=\frac{1}{2}\mathrm{l}\mathrm{n}\left(\frac{1-{\epsilon }_1}{{\epsilon }_1}\right) \]$

(8)

$\[ D_2\left(i\right)=\frac{1}{z}{D}_1\left(i\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\alpha }_1,y_1\widehat{y_1}\right) \]$

(9)

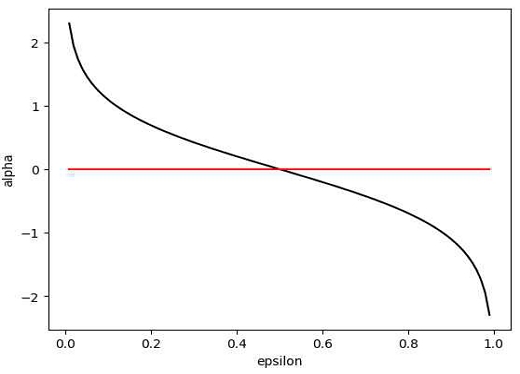
여기서 I(A≠B)는 If(A≠B) 1, Else 0인 함수로 식 (7)은 오 분류된 사건만의 가중치를 모두 더한 것이고, 식 (8)은 그림 3과 같이 에러가 0.5보다 약간 좋은 약한 분류기(ε<0.5)에서 α>0이 되도록 한다. 또한 식 (9)는 다음 모델을 위한 샘플 가중치를 구하는 것으로 오 분류된 사건에 해당하는 가중치를 높여 다음 학습에 선택될 확률을 높이고, 올바르게 분류된 사건에는 가중치를 내리기 위한 정책을 반영한 식이다. 그리고 z는 일반화 상수로 각 사건의 가중치를 모두 더한 값이며 가중치(D)가 확률이므로 [0,1] 범위에서 결정되도록 하는 역할을 한다.

Fig. 3.

Relationship between α(alpha) and ε(epsilon)

여러 개(T개)의 가설 모델들로부터 정보를 모아 강한 분류기가 되기 위한 결과를 산출하는 과정으로 다음과 같다.

$\[ H\left(x\right)=sign\left(\sum _{t=1}^T{\alpha }_t{h}_t\left(x\right)\right) \]$

(10)

식 (10)에서 h_t(x)는 t번째 모델의 추정치이며 α와는 반비례 관계가 있다. 즉 추정치에 오류가 많으면 α는 작고, 반대로 오류가 적으면 α는 크게 되어 이를 전부 합하면 올바르게 판단된 추정치가 더 큰 역할을 하도록 한다는 것이다.

Ⅳ. 실 험

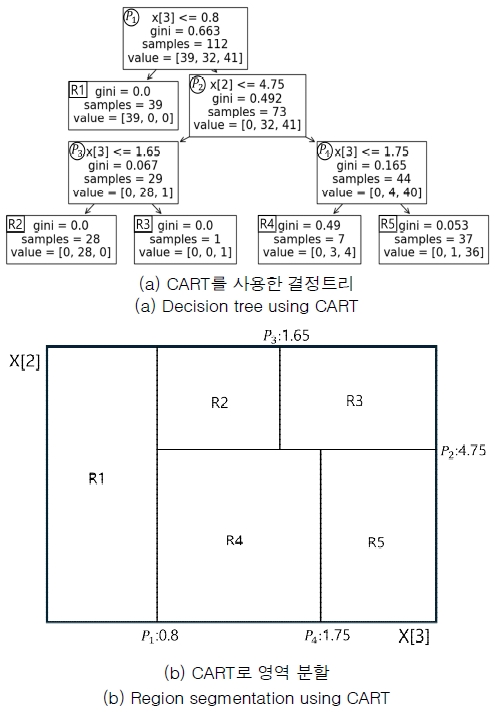
본 논문의 에이다부스트에서 약한 분류기로 사용하는 CART와 LDA에 대해서는 2장에서 서로의 특징을 설명하였다. 이에 대한 실험 결과를 비교하기 위해 학습 과정을 먼저 살펴본다. 우선 지니 계수를 기반으로 하는 결정트리는 이진 트리구조를 가지며, 그림 4에서 IRIS 데이터를 약한 분류기에 입력하여 학습하는 과정을 예로 설명한다. 이 데이터는 4개의 속성값을 가지나 간단히 2, 3번째 속성(X[2], X[3])만으로 결정트리를 구성하는 노드의 예로, 그림 4의 (a)는 깊이를 3으로 하는 경우를 나타낸다. 각 노드 중에 루트 노드의 첫째 줄 “X[3] <= 0.8”은 3번째(4개중) 속성이 0.8보다 작거나 같을 때를 의미하는 것으로 왼/오른쪽의 결정트리로 분리하기 위한 최적의 분리점을 의미한다. 둘째 줄은 이때의 지니 계수를 의미하며, 세 번째는 이 노드에서의 사건 수를 의미한다. 마지막으로 “value=[39,42,41]”은 IRIS 데이터의 부류 중 부류 1의 사건 수가 39, 부류 2, 3의 사건 수가 각각 42, 41을 의미한다. 마지막 말단 노드에서 “value=[0,3,4]”와 같이 부류 2와 부류 3이 같이 존재하여 임의의 노드에서 부류가 완전하게 분류되지 않은 것을 볼 수 있는데 이는 트리의 깊이를 3으로 제한하여 학습 중에 절단이 일어났기 때문이다. 그리고 그림 4의 (b)에서는 (a)의 결정트리로 분류된 데이터 영역을 의미하는 것으로 루트 노드로부터 말단 노드에 이르기까지 분리면에 따라 영역이 분류된 것을 볼 수 있다. 여기서 분류면이 각 축에 따라 직각으로 분류하고 있음을 볼 수 있다.

Fig. 4.

Learning of CART decision tree

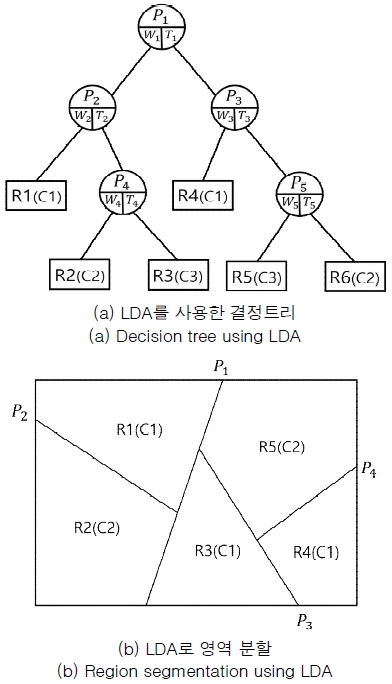
반면 그림 5의 (a)는 임의의 데이터를 LDA로 학습한 경우의 결정트리를 낸다. CART의 결정트리와 같이 이진 트리 형식을 가지며 임의의 노드는 식 (2)에서 B/V를 최대로 하는 공분산 행렬 W와 식 (5)와 같이 투영(W^TX)된 포인트 들 중에서 최적의 분류면을 결정하는 스칼라값인 Th_i로 구성된다. 각 데이터는 식 (6)과 같이 왼/오른쪽으로 분류하며 결정트리를 구성해 간다. 그림 5에서 (b)는 (a)의 결정트리에 따라 분류된 영역을 나타내는데 그림 4 (b)의 영역과 비교하면 분류면이 속성축과 관계없이 임의의 각을 가지는 특성을 가진다. 이는 분류면의 각은 각 노드에서 W와 T_i에 의해 결정되는 LDA 결정트리의 특징으로 그림 4의 결정트리와 비교하여 성능에 영향을 미친다. 이에 대해서는 실험 데이터로 결과를 비교한다.

Fig. 5.

Decision tree learning of LDA

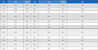
실험을 위해 사용한 데이터는 표 1에 표시된 바와 같이 UCI 기계저장소[12]의 데이터(bs, car_num)와 인간의 수면 상태를 11개의 센서로 수집한 후 양자화한 데이터(sleep)을 사용하였다. 이들 데이터의 실험 결과를 위해 10겹 교차검증 방법을 사용하였고 그 결과가 표 2에 나타나 있다. 그리고 각 데이터에 따라 결과들의 비교를 위한 그래프가 그림 6에 나타나 있다.

Table 1.

Data used in the experiment and its characteristics

Table 2.

The results of the experiment using AdaBoost with two types of decision trees as weak classifiers

Fig. 6.

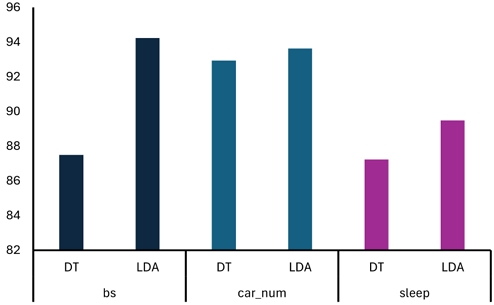
A graph representing Table 2, which compares the performance of two decision tree algorithms on the experimental data using 10-fold cross-validation

실험 결과 정도의 차이는 있으나 실험한 모든 데이터에서 LDA의 결과가 우수한 것을 볼 수 있다. 이는 CART와 유사한 방식인 속성축과 직교로 분류하는 C4.5를 이용한 전 연구[13],[14]에서도 확인할 수 있었는데, 분류면을 속성축에 고정하는 것 보다는 속성값에 따라 자유롭게 각을 가지도록 하여 근사 최적을 분류면을 구한 결과로 해석한다.

Ⅴ. 결 론

지금까지 에이다부스트 알고리즘의 약한 분류기에서 출발하여 오류를 포함하는 사건을 강화하는 방법을 반복하여 강한 분류기로 진화하는 과정을 살펴보았다. 요즘 분류 알고리즘의 성능 향상을 위해서 뛰어난 하나의 알고리즘보다는 여러 분류기의 힘을 합하여 하나의 결론에 이르게 하는 앙상블이 대세가 되고 있다.

본 논문에서는 에이다부스트의 약한 분류기를 위해 일반적으로 사용되는 CART와 CART 대신 Fisher의 선형판별함수로부터 유도된 LDA로 대체하는 2가지 결정트리 구성 방법과 이를 앙상블에 적용하는 이론적인 배경에 대해 알아보았다. 그리고 2가지 결정트리를 적용할 때의 결과에 대해서도 알아보았고 실험에 사용한 학습 데이터에서 LDA의 결과가 다소 우수한 것으로 나타났다. 이러한 결과는 C4.5, CART와 비교하여, LDA가 학습이 이루어짐에 따라 결정트리의 노드를 결정하는 과정에서 선형 분리면으로 공간을 분할하는 방법의 차이에서 오는 결과라고 해석한다.

최근의 앙상블 알고리즘 중에 이용도가 높고 따라서 미래의 대세가 될 Random Forest, GBM, XGBoost, LGBM 알고리즘과 결합하여 성능을 높이려는 연구가 다방면으로 이루어지고 있다[15],[16]. 이러한 연구의 하나로 앙상블 알고리즘들이 CART 결정트리를 기본으로 하고 있으나 이를 본 논문에서 소개한 LDA와 같은 결정트리도 적용해 볼 수 있을 것이다. 또한 전처리로 LDA를 이용하여 차원 축소를 한 후 딥러닝과 같은 다양한 학습을 수행하는 연구들도 앞으로의 연구 주제가 될 수 있을 것으로 본다.

References

• Y. Freund, “Boosting a Weak Learning Algorithm by Majority,” Information and Computation, Vol. 121, No. 2, pp. 256-285, September 1995. [https://doi.org/10.1006/inco.1995.1136]
• Y. Freund and R. E. Schapire, “A Short Introduction to Boosting,” Journal of Japanese Society for Artificial Intelligence, Vol. 14, No. 5, pp. 771-780, September 1999.
• A. Tharwat, T. Gaber, A. Ibrahim, and A. E. Hassanien, “Linear Discriminant Analysis: A Detailed Tutorial,” AI Communications, Vol. 30, No. 2, pp. 169-190, 2017. [https://doi.org/10.3233/AIC-170729]
• W. Loh and N. Vanichsetakul, “Tree-structured Classification via Generalized Discriminant Analysis,” Journal of the American Statistical Association, Vol. 83, No. 403, pp. 715-728, 1988. [https://doi.org/10.2307/2289295]
• L. Breiman, J. Friedman, R. A. Olshen, and C. J. Stone, Classification and Regression Trees, New York: Chapman and Hall/CRC, 1984. [https://doi.org/10.1201/9781315139470]
• R. Rojas, “AdaBoost and the Super Bowl of Classifiers A Tutorial Introduction to Adaptive Boosting,” Freie University, Berlin, Tech Rep 1, Vol. 1, pp. 1-6, 2009. [https://doi.org/10.36227/techrxiv.172107276.63524590/v1]
• J. Zhu, H. Zou, S. Rosset, and T. Hostie, “Multi-Class AdaBoost,” Statistics and Its Interface, Vol. 2, pp. 349-360, 2009. [https://doi.org/10.4310/sii.2009.v2.n3.a8]
• T. Chen and C. Guestrin, “XGBoost: A Scalable Tree Boosting System,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 785-794, 2016. [https://doi.org/10.1145/2939672.2939785]
• L. Breiman, “Random Forests,” Machine Learning, Vol. 45, pp. 5-32, 2001. [https://doi.org/10.1023/A:1010933404324]
• J. H. Friedman, “Greedy Function Approximation: A Gradient Boosting Machine,” The Annals of Statistics, pp. 1189-1232, October 2001. [https://doi.org/10.1214/aos/1013203451]
• G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, ... and T. Liu, “LightGBM: A Highly Efficient Gradient Boosting Decision Tree,” in 31st Conference on Neural Information Processing Systems, pp. 3149-3157, 2017.
• University of California, Irvine. UCI Machine Learning Repository [Internet]. Available: https://archive.ics.uci.edu/ml/index.php, .
• J. C. Lee, “Comparison of Two Classifiers for Handling Incomplete Data with Decision Trees: C4.5, SVM,” Journal of Knowledge Information Technology and Systems, Vol. 18, No. 1, pp. 71-80, 2023. [https://doi.org/10.34163/JKITS.2023.18.1.008]
• J. C. Lee, “Algorithm to Handling Incomplete Data from Decision Tree Using SVM,” Journal of Knowledge Information Technology and Systems, Vol. 17, No. 6, pp. 1145-1153, 2022. [https://doi.org/10.34163/JKITS.2022.17.6.006]
• P. Deng, H. Wang, T. Li, S. Horng, and X. Zhu, “Linear Discriminant Analysis Guided by Unsupervised Ensemble Learning,” Information Sciences, Vol. 480, pp. 211-221, April 2019. [https://doi.org/10.1016/j.ins.2018.12.036]
• R. Garf, M. Zeldovich, and S. Friedrich, “Comparing Linear Discriminant Analysis and Supervised Learning Algorithms for Binary Classification—A Method Comparison Study,” Biometrical Journal, Vol. 66, No. 1, pp. 1-20, January 2024. [https://doi.org/10.1002/bimj.202200098]