겹치는 정도가 높은 학습데이터에서 오토인코더 은닉층 확장의 영향 분석

Ⅰ. 서 론

최근 머신 러닝과 딥 러닝은 끊임없이 발전하고 있으며 특히 딥러닝은 일상생활부터 의료, 기계 설비 등 전문적인 분야까지 다양한 분야에서 복잡한 문제를 해결하는 방법으로 자리 잡고 있다[1]. 딥러닝 모델의 학습 방법의 하나인 비지도 학습(Unsupervised learning)은 정답 값이 주어지는 지도 학습(Supervised learning)과 달리 정답 없이 학습이 진행된다. 비지도 학습의 대표적인 모델인 오토인코더(AE; Auto-Encoder)는 입력 데이터를 더 낮은 차원의 잠재 벡터(Latent vector)로 압축한 뒤 다시 입력 데이터와 최대한 유사한 출력을 재구성하도록 학습되며, 이를 통해 차원 축소(Dimensionality reduction)[2], 특징 추출(Feature extraction)[3], 이상치 탐지(Anomaly detection)[4] 등과 같은 분야와 노이즈 제거(Noise reduction)[5] 또는 생성모델(Generative model)[6]에서 널리 사용되고 있다[1],[11].

하지만 AE와 딥러닝 모델이 더욱 높은 차원의 데이터를 다루게 되면서 각 클러스터 간 겹치는 정도가 높은 학습데이터를 다루게 되고, 이에 따라서 성능이 떨어진다는 문제가 있다[7]. 본 논문에서는 AE의 첫 번째 은닉층의 차원을 크게 확장하면 이러한 문제가 완화될 것이라는 가설하에 첫 번째 은닉층의 차원 확장에 따른 AE의 성능을 분석하였다.

일반적으로 딥러닝 실험에 많이 사용하는 데이터셋인 MNIST[8]나 CIFAR10[9] 등의 학습데이터는 각 클러스터 간 겹침 정도를 측정하기 어렵고 제어하기는 불가능하다. 따라서 본 논문에서는 겹침 정도에 따른 인위적인 데이터를 생성하는 방법을 고안하여 학습 데이터를 만들어 실험하였다. 3가지 방식으로 3가지 겹침 정도에 따른 학습 데이터를 만들었다. 또한 다양한 은닉층 확장 모델을 구현하여 실험하였다. 실험 결과 겹침 정도가 증가할수록 은닉층의 차원을 더 크게 확장한 AE의 성능이 좋아짐을 확인하였다. 이러한 결과를 통하여 본 논문에서 제시한 가설이 옳다는 것을 확인할 수 있었다.

인공 데이터 뿐만이 아닌 MNIST, FashionMNIST와 같은 일반 데이터셋에서도 성능을 측정하였는데, 이때도 일반적으로 은닉층을 확장한 AE가 성능이 더 좋음을 확인하였다. 마지막으로 비지도 학습이 아닌 지도 학습에서의 성능을 확인하기 위하여 AE로 추출된 특징을 이용하여 분류하는 분류 문제에 대해 실험하였다[10]. 실험 결과 겹침 정도가 높을수록 은닉층을 확장한 특징추출기를 사용하였을 때 분류성능이 좋아짐을 확인하였다.

Ⅱ. 실험데이터와 모델

2-1 인공 데이터

제안된 모델이 기존 AE에 비해 클러스터 간 겹치는 정도가 심한 데이터셋에서 더 좋은 성능을 보이는지 확인하기 위해서 겹치는 정도를 조절할 수 있는 인공 데이터를 생성하여 실험하였다. 인공 데이터는 평균 벡터와 공분산 행렬을 매개변수로 가지는 다변량 정규 분포(Multivariate normal distribution)에서 추출하여 사용한다. C개의 클래스에 대해서 각 D차원 데이터를 총 N개 생성하며 각 클래스의 중심 위치는 평균 벡터 통해 구분되고, 겹치는 정도는 분산과 공분산을 통해 조절된다.

1) 데이터 중심 위치

본 논문에서는 인공 데이터의 각 클래스에 속하는 데이터의 중심 위치를 결정하는 평균 벡터를 Interval, Uniform, Normal 3가지 방법으로 결정하였다.

• Interval

Interval 방식은 각 클래스의 중심 위치를 수식 (1)과 같이 주어진 중심 위치의 범위인 (-a,a)를 동일한 간격으로 분할하여 결정된다. 예를 들어 a = 10, C = 3인 경우 각 클래스 c의 평균 벡터 μ_c(1 ≤ c ≤ C)는 μ₁ = -10,μ₂ = 0,μ₃ = 10이다.

$\[ {\mu }_{c,j}=-a+\frac{2a}{C-1}\left(c-1\right)\text{ for }j=\mathrm{1,2},\cdots ,D \]$

(1)

• Uniform

Uniform 방식은 수식 (2)와 같이 각 클래스의 중심 위치를 주어진 중심 위치의 범위인 (-a,a)를 파라미터로 가지는 균일 분포(Uniform distribution)에서 추출한다.

$\[ {\mu }_{c,j}\sim U\left(-a,a\right)\text{ for }j=\mathrm{1,2},\cdots ,D \]$

(2)

• Normal

Normal 방식은 Uniform 방식과 비슷하지만, 수식 (3)에서 보이는 것처럼 평균이 0이고 주어진 중심 위치 범위의 상한인 a를 표준편차로 가지는 정규분포(Normal distribution)에서 추출한다.

$\[ {\mu }_{c,j}\sim N\left(0,a\right)\text{ for }j=\mathrm{1,2},\cdots ,D \]$

(3)

2) 공분산 행렬

다변량 정규 분포의 매개변수 중 공분산 행렬의 대각 성분은 분산으로 해당 변수의 데이터가 얼마나 넓게 퍼져있는지를 나타내고 공분산은 변수 간의 상관관계를 나타내어 어느 방향으로 퍼져있는지를 나타낸다. 본 논문에서는 위와 같은 2가지 특징을 통해 데이터의 겹치는 정도를 조절하였다.

• 분산

데이터의 각 클래스의 중심 위치가 고정되어 있을 때 분산의 크기에 따라 데이터 공간에서의 겹치는 정도가 달라진다. 이때 D차원 항등 행렬(Identity matrix) I_D와 분산에 의한 겹치는 정도를 O_V라고 할 때 클래스 c에 해당하는 공분산 행렬 Σ_c는 수식 (4)와 같다.

$\[ {\Sigma }_c=I_D\times \left(O_V+1\right) \]$

(4)

• 공분산

데이터의 각 클래스의 중심 위치가 고정되어 있을 때 공분산의 크기가 커질수록 조금 더 실제 데이터와 비슷한 모양의 분포를 그리게 된다. 이때 D차원 항등 행렬(Identity matrix) I_D와 분산에 의한 겹치는 정도를 O_C, 가우시안 노이즈를 통해 생성한 D차원 노이즈 행렬 E에 대해 클래스 c에 해당하는 공분산 행렬 Σ_c는 수식 (5)와 같다.

$\[ {\Sigma }_c=I_D+O_C\times E\cdot E^T \]$

(5)

3) 인공 데이터 생성

수식 (6)과 같이 위에서 소개한 평균 벡터와 공분산 행렬을 매개변수로 가지는 다변량 정규 분포에서 각 클래스에 속하는 데이터를 추출한다.

$\[ \begin{array}{c}{X}_c\sim N\left({\mu }_c,{\Sigma }_c\right)=\hfill \\ \frac{1}{{\left(2\pi \right)}^{\frac{D}{2}}{\left|{\Sigma }_c\right|}^{\frac{1}{2}}}\text{exp}\left(-\frac{1}{2}{\left(x-{\mu }_i\right)}^T{\Sigma }_i^{-1}\left(x-{\mu }_i\right)\right)\hfill \end{array} \]$

(6)

4) 생성된 인공 데이터 샘플

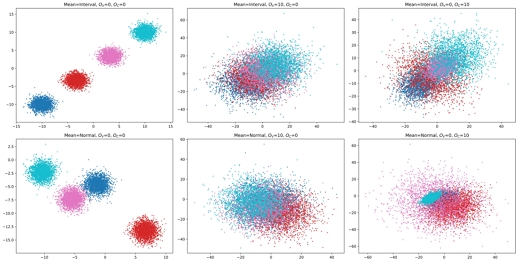
지금까지 소개한 인공 데이터 생성 방법에 따라서 2차원의 데이터 샘플을 생성 및 시각화 하였다. 그림 1의 위 3개의 샘플은 Interval방식을 통해 평균 벡터를 결정하였고, 아래 3개의 샘플은 Normal방식을 통해 결정하였다. 또한 가장 좌측 2개의 샘플은 O_V = 0, O_C = 0을 가지고, 중간에 있는 2개의 샘플은 O_V = 10, O_C = 0을, 마지막으로 가장 우측 2개의 샘플은 O_V = 10, O_C = 10을 가진다.

Fig. 1.

Artificial data samples generated in two-dimensions

Fig. 2.

Model structure of AE(left) and IEAE(right)

2-3 모델 구조

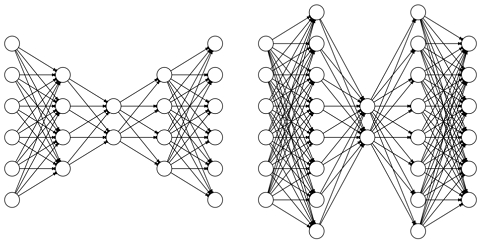
실험에 사용된 모델은 baseline모델인 AE와 본 논문에서 제안하는 모델인 첫 번째 은닉층을 확장한 IE(Input Expansion)AE이다. 두 모델은 은닉층의 구조를 제외하면 모두 같은 하이퍼 파라미터(Hyper parameter)를 공유한다. 은닉층의 활성화 함수는 ReLU를 사용하며, 출력층의 경우 Sigmoid를 활성화 함수로 사용한다. AE의 경우 입력층부터 잠재 벡터까지 은닉층의 노드 개수가 줄어들지만, IEAE의 경우 은닉층 중 한 개의 레이어가 입력층보다 더 큰 차원을 가지게 된다.

딥러닝 모델에서 가중치의 개수는 성능에 중요한 요소이다. AE와 IEAE가 비슷한 가중치 개수를 가지는 상태에서 실험하기 위해 가능한 한 유사한 가중치 개수를 가지도록 모델을 구성하였다.

1) AE

Baseline모델인 AE는 두 가지의 다른 모델을 고안하여 실험하였다. 그 중 AE-1의 경우 다음과 같은 모델 구조를 가진다.

• Encoder: 784 → 650 → 512 → 450 → 350 → 320 → LD
• Decoder: LD → 320 → 350 → 450 → 512 → 650 → 784

반면 AE-2의 경우 AE-1의 깊이가 깊다는 점을 반영하여 가중치의 개수를 무시, 레이어의 깊이만을 고려하도록 구성하였다.

• Encoder: 784 → 512 → 256 → LD
• Decoder: LD → 256 → 512 → 784

2) IEAE

본 논문에서 제안하는 IEAE의 구조는 다음과 같이 구성하였다.

• Encoder: 784 → 1024 → 512 → LD
• Decoder: LD → 512 → 1024 → 784

위 AE와 IEAE의 구조에서 LD는 잠재 벡터의 차원으로 본 논문에서는 2, 16, 64의 값에 대해 실험하였다.

3) 훈련 가중치 개수

AE-1과 IEAE가 서로 비슷한 가중치 개수를 가지게 하도록 AE-1의 레이어 깊이를 더욱 깊게 만들어 실험하였다. 표 1은 LD의 값이 64일 때 AE-1, AE-2, IEAE의 총 훈련 가중치 개수와 모델의 용량을 비교한 표이다.

Table 1.

Training parameters and model capacity of 3 models

Ⅲ. 실험 결과 및 결과 분석

3-1 인공 데이터 실험 결과

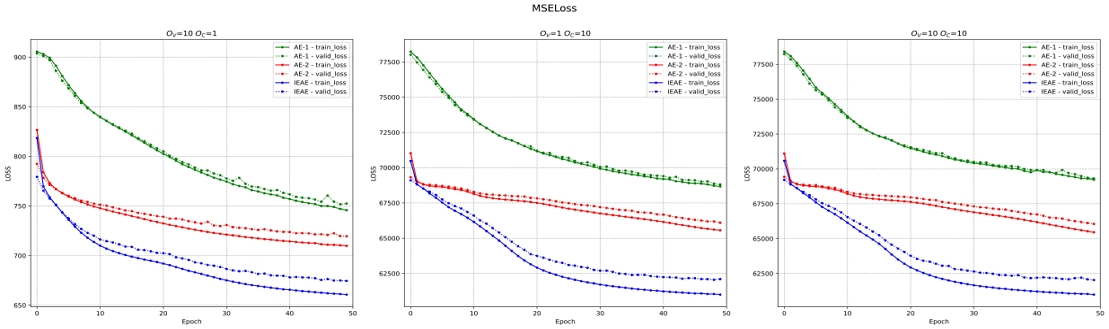
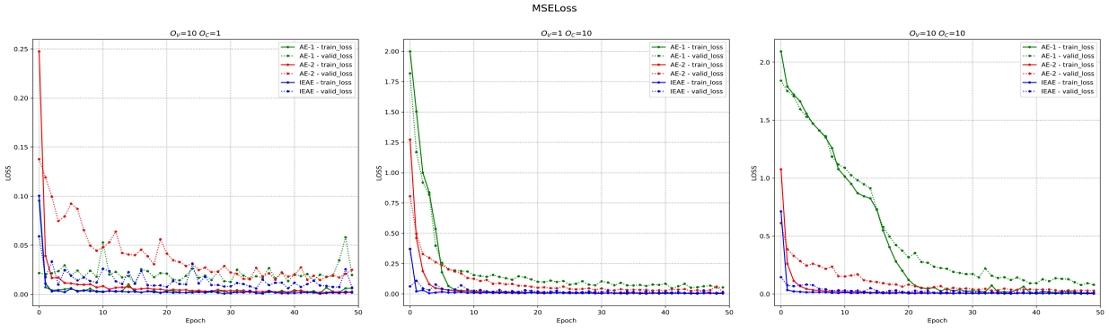
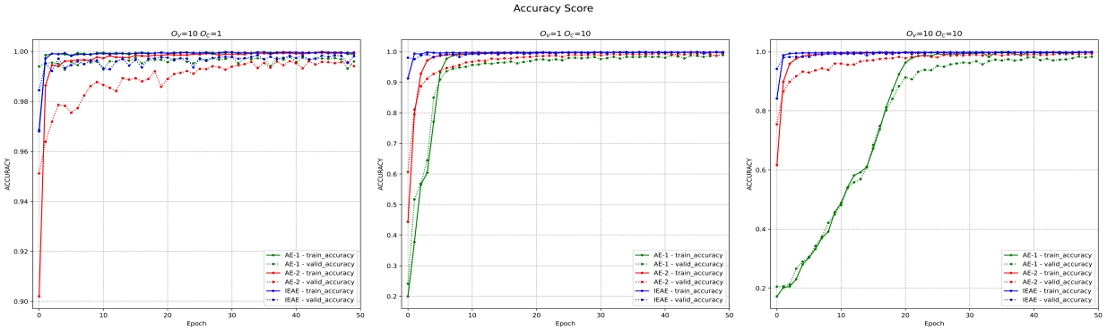
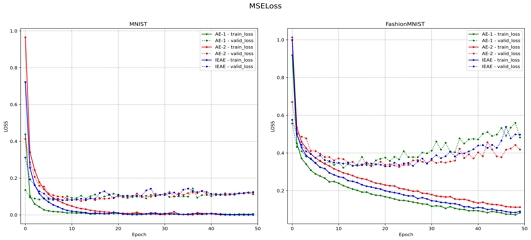
실험에 사용된 인공 데이터는 데이터의 개수, O_C, O_V, 데이터 평균 결정 방법을 다양하게 조절, 생성하여 실험하였다. 본 논문에서는 데이터의 겹침 정도에 따른 성능 평가를 위해 평균 결정 방법을 Interval로 고정하였고, 총 데이터의 개수 300,000개에서 훈련용 데이터를 240,000개 검증용 데이터를 60,000개로 설정하여 실험하였다. 그림 3의 손실 함수의 값을 보았을 때 충분히 데이터가 겹친 상황에서 AE 모델에 비해 IEAE 모델의 재구성 손실 함수의 값이 더 낮은 걸 확인할 수 있다. 특히 O_C의 값이 큰 경우 AE와 IEAE의 성능 차이가 더 크게 나타나는 걸 볼 수 있다. 학습 시간의 경우 계층 수가 동일한 AE-2와 IEAE 가 유사하였으며 계층 수가 가장 많은 AE-1가 가장 오래 걸렸다.

Fig. 3.

Reconstruction loss for artificial data

3-2 실제 데이터 실험 결과

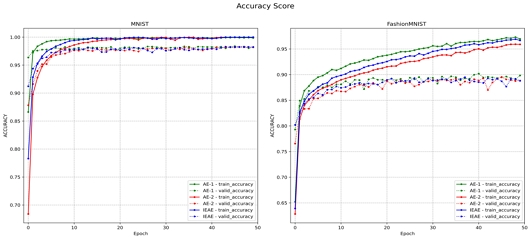
인공 데이터가 아닌 실제 데이터인 MNIST와 FashionMNIST에 대해서 동일한 실험을 진행했다. 실제 데이터에 관한 실험에서는 재구성 손실과 함께 이미지 재구성에 관한 수치를 추가하여 비교했다.

1) 재구성 손실

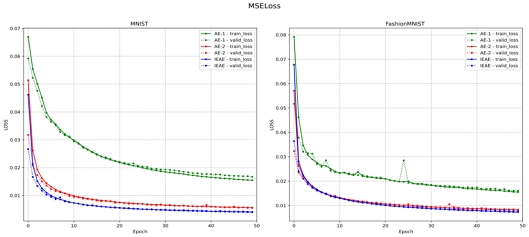
그림 3을 보면 실제 데이터에 대한 실험에서도 IEAE가 AE-1과 AE-2에 비해서 더 낮은 손실을 보이는 걸 확인할 수 있다.

Fig. 4.

Reconstruction loss for MNIST(left) and FashionMNIST(right)

2) 이미지 재구성 점수

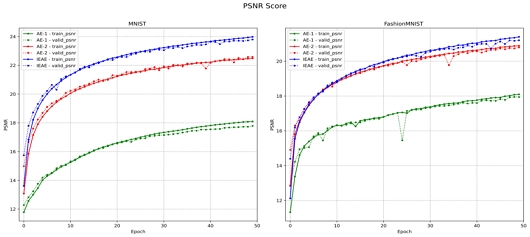
실제 데이터를 통한 실험에서는 이미지 생성 모델에서 사용되는 이미지 품질 평가 수치 PSNR(Peak Signal-to-Noise Ratio)[12]과 SSIM(Structural Similarity Index Map)[12] 2가지를 함께 사용하여 이미지 재구성 능력에 대해 평가하였다. PSNR은 신호가 가질 수 있는 최대치에 대해 잡음의 비율을 나타낸 것이며, 이미지의 경우 각 픽셀이 가질 수 있는 최대값(8-bit Grayscale의 경우 255)에 대해 잡음이 얼마나 많은지에 대한 수치이다. PSNR수치가 높을수록 품질이 좋은 이미지라고 볼 수 있다. PSNR 점수를 그래프로 나타낸 그림 5를 보면 IEAE가 두 개의 AE모델보다 더욱 높은 점수를 보인다. 이는 IEAE가 재구성한 이미지의 품질이 AE가 재구성한 이미지의 품질보다 좋다는 걸 의미한다.

Fig. 5.

PSNR scores for MNIST(left) and FashionMNIST(right)

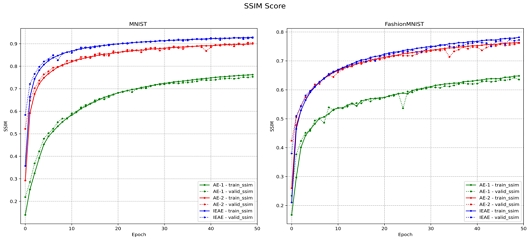
SSIM은 휘도, 대비, 픽셀의 구조 3가지 관점에서 두 이미지를 비교하는 척도로써 인간의 시각 기관이 이미지를 인식하는 방법에서 착안된 방법이다. SSIM은 0과 1사이의 값을 가지고, 1에 가까울 수록 두 이미지는 유사하다. 그림 6에서 MNIST와 FashionMNIST에 대한 SSIM 점수를 보면 IEAE가 두 개의 AE모델보다 더 높은 SSIM 점수를 가지고 있음을 볼 수 있다. 이는 IEAE가 AE모델에 비해 재구성하는 능력이 뛰어남을 나타낸다.

Fig. 6.

SSIM scores for MNIST(left) and FashionMNIST(right)

3-3 분류문제 실험 결과

AE와 IEAE의 성능을 비교하기 위해서 인공 데이터와 실제 데이터에 대해서 분류 문제 실험을 진행하였다. 이 실험은 AE의 응용 중 하나로 AE를 비지도 학습 방법으로 사전 학습(Pre-training)시킨 뒤 분류 문제를 위한 FC Layer(Fully connected layer)를 AE의 인코더 부분에 결합하여 미세조정을 통해 분류 문제에 최적화시키는 방법이다[10].

1) 인공 데이터 분류 결과

그림 7과 그림 8은 인공 데이터에 대한 분류 문제의 MSE 손실과 정확도이다. 결과를 보면 손실과 정확도 모두 훈련이 진행될수록 세 가지 모델 모두 비슷한 값으로 수렴하지만, IEAE의 수렴 속도가 가장 빠른 걸 확인할 수 있다.

Fig. 7.

Classification problem MSE loss for artificial data

Fig. 8.

Classification problem accuracy for artificial data

2) 실제 데이터 분류 결과

그림 9와 그림 10은 MNIST와 FashionMNIST에 대한 분류 문제의 MSE 손실과 정확도이다. 인공 데이터에 비해 데이터 공간상 겹침이 심하지 않아 세 가지 모델 모두 비슷한 수치를 보인다.

Fig. 9.

Classfication problem loss for MNIST(left) and FashionMNIST(right)

Fig. 10.

Classification problem accuracy for MNIST(left) and FashionMNIST(right)

Ⅳ. 결 론

본 논문에서는 AE의 첫 번째 은닉층의 차원을 입력 차원보다 크게 하였을 때 학습데이터의 클러스터가 심하게 겹치는 데이터셋에서 어떤 효과를 주는지를 분석하였다. 이를 확인하기 위해서 겹치는 정도를 조절할 수 있는 인공적인 데이터를 생성하여 겹치는 정도에 따른 성능을 측정하였다. 실험 결과 AE의 첫 번째 은닉층의 차원을 확장한 IEAE가 겹치는 정도가 심한 데이터에서 AE에 비해 성능이 더 좋아짐을 확인하였다. 또한 AE로 추출된 특징을 통한 분류 문제에서도 입력 확장의 효과가 있음을 확인하였다. MNIST와 FashionMNIST에 대한 손실 함숫값과 PSNR, SSIM과 같은 이미지 품질 평가에서도 이미지 재구성 능력이 향상되었다. 이런 결과를 보았을 때 AE와 비슷한 구조를 가진 VAE 모델에서도 효과가 있을 것으로 기대된다.

Acknowledgments

본 연구는 한성대학교 학술연구비 지원과제입니다.

본 논문의 내용은 2024년 한국디지털콘텐츠학회 하계학술대회에서 발표한 “IEAE: 입력 확장을 통한 오토인코더 성능 향상” 연구를 확장하여 실험하고 분석하여 작성하였습니다.

References

• K. Berahmand, F. Daneshfar, E. S. Salehi, Y. Li, and Y. Xu, “Autoencoders and Their Applications in Machine Learning: A Survey,” Artificial Intelligence Review, Vol. 57, No. 2, 28, February 2024. [https://doi.org/10.1007/s10462-023-10662-6]
• Y. Wang, H. Yao, and S. Zhao, “Auto-Encoder Based Dimensionality Reduction,” Neurocomputing, Vol. 184, pp. 232-242, April 2016. [https://doi.org/10.1016/j.neucom.2015.08.104]
• Q. Meng, D. Catchpoole, D. Skillicorn, and P. J. Kennedy, “Relational Autoencoder for Feature Extraction,” in Proceedings of 2017 International Joint Conference on Neural Networks, Anchorage, AK, pp. 364-371, May 2017. [https://doi.org/10.1109/IJCNN.2017.7965877]
• C. Zhou and R. C. Paffenroth, “Anomaly Detection with Robust Deep Autoencoders,” in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, Canada, pp. 665-674, August 2017. [https://doi.org/10.1145/3097983.3098052]
• P. Vincent, H. Larochelle, Y. Bengio, and P.-A. Manzagol, “Extracting and Composing Robust Features with Denoising Autoencoders,” in Proceedings of the 25th International Conference on Machine learning, Helsinki, Finland, pp. 1096-1103, 2008. [https://doi.org/10.1145/1390156.1390294]
• D. P. Kingma and M. Welling, “Auto-Encoding Variational Bayes,” arXiv preprint arXiv:1312.6114, , 2013. [https://doi.org/10.48550/arXiv.1312.6114]
• P. Vuttipittayamongkol, E. Elyan, and A. Petrovski, “On the Class Overlap Problem in Imbalanced Data Classification,” Knowledge-Based Systems, Vol. 212, 106631, January 2021. [https://doi.org/10.1016/j.knosys.2020.106631]
• Y. LeCun, C. Cortes, and C. J. C. Burges. The MNIST Database of Handwritten Digits [Internet]. Available: http://yann.lecun.com/exdb/mnist/
• A. Krizhevsky and G. Hinton, Learning Multiple Layers of Features from Tiny Images, University of Toronto, Toronto, Canada, Technical Report, 2009.
• M. Gogoi and S. A. Begum, “Image Classification Using Deep Autoencoders,” in Proceedings of 2017 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, December 2017. [https://doi.org/10.1109/ICCIC.2017.8524276]
• T. Li, R. Mehta, Z. Qian, and J. Sun, “Rethink Autoencoders: Robust Manifold Learning,” in Proceedings of the ICML 2020 Workshop on Uncertainty and Robustness in Deep Learning, 2020.
• W. Preedanan, T. Kondo, P. Bunnun, and I. Kumazawa, “A Comparative Study of Image Quality Assessment,” in Proceedings of 2018 International Workshop on Advanced Image Technology, Chiang Mai, Thailand, January 2018. [https://doi.org/10.1109/IWAIT.2018.8369657]