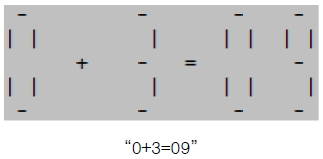성냥개비 등식 퍼즐 게임 알고리즘 설계 및 구현

Ⅰ. 서 론

성냥개비는 기원전 3,500년 경 이집트인들이 가연성 유황 혼합물로 코팅된 작은 소나무 막대를 만들었고, 서기 1,400년 경 가연성 화학 물질을 코팅한 코드나 전선을 만들었다는 데에서 유래한다. 현대적인 성냥개비는 1,805년 파리에서 루이 자크 테나르(Louis Jacques Thenar) 교수의 조수였던 샤넬(K. Chanel)에 의해 발명되었다[1]. 이후 진보를 거듭한 성냥개비는 불을 붙이는 기본적인 용도 외에 특정 모양을 만들고 그림을 그리는 것뿐만 아니라 브레인스토밍 퍼즐과 퀴즈를 만드는 등 다양한 분야에 사용된다. 이중 성냥개비 퍼즐은 장소의 구애를 받지 않고, 남녀노소 부담 없이 즐길 수 있는 보편화된 놀이 중의 하나이다. 이 게임은 단순한 흥미 위주를 벗어나 건전한 수학적 두뇌 활동에도 도움을 준다[2]. 성냥개비 퍼즐 놀이 중 어린이들의 수학적 두뇌 활동과 관련이 깊은 등식 맞추기 게임을 들 수 있다.

이 연구에서는 성냥개비를 이용한 등식 맞추기 퍼즐 게임을 위한 알고리즘을 개발하고 실험한다. 이를 위하여 II 장에서 성냥개비의 활용 분야를 살펴보고, III 장에서 등식 맞추기 게임을 위한 기본 자료구조를 제시하며, IV 장에서 등식 탐색을 위한 알고리즘을 설계·구현하고 평가한다. 그리고 마지막 V 장의 결론으로 이 논문을 맺는다.

Ⅱ. 성냥개비 활용 게임

근대 이래 성냥개비의 활용 분야는 다양하다. 우선 학문적인 측면에서의 활용은 기업 경영의 공급망 관리를 위한 시뮬레이션 게임을 들 수 있다[3]-[5]. 이들 게임에서 성냥개비는 각종 제품이나 재화의 재고 상황 및 교환 수단으로 유용하게 활용된다. 성냥개비를 이용한 영어 어휘 교수학습법[6]은 성냥개비로 만드는 모형이나 그림을 이용하여 학습 성과를 높인다. 성냥개비는 모형이나 미니어처 제작에도 활용되는데, 최근에 제작된 7.2 m 높이의 에펠탑이 그 대표적인 예이고[7], 그밖에 여러 가지 모형 제작에 이용된다[8].

성냥개비의 원래 목적 외 대중적 활용 분야는 무엇보다도 퍼즐 게임이다. 수학적 이론을 배경으로 하는 대표적인 퍼즐 게임으로 성냥개비 줄여가기 게임을 들 수 있다[9],[10]. 이 게임은 A, B 두 사람이 N개의 성냥개비 더미에서 1~ m개를 번갈아 제거하되 마지막 차례에 제거하게 되는 사람이 이기는 규칙으로 진행되는데, N%(m+1)이 0이면 B가 이길 수 있고, 그렇지 않은 경우 첫 시도에서 A가 N%(m+1) 개를 제거하면 A가 이길 수 있음을 증명할 수 있다.

‘0’~‘9’의 숫자를 의미하는 길이가 서로 다른 성냥개비 열 개를 종이상자에 임의의 순서로 꽂아두고 한 사람이 한 번씩 자리를 바꿔가면서 가장 큰 수를 만드는 사람이 이기는 게임도 있는데, 흥미를 더 높이기 위해 성냥개비 대신 다양한 수치 표현 진법으로 원래의 숫자를 은유해서 적은 카드를 이용하기도 한다[11].

남녀노소 누구라도 장소와 시간에 구애받지 않고 즐길 수 있는 성냥개비 게임 유형은 주어진 초기 배치에서 성냥개비 몇 개를 옮겨 조건에 맞게 변환시키는 퍼즐 게임이다. 요구 조건은 크게 기하학적 도형과 등식 맞추기로 나눌 수 있다. 성냥개비를 옮겨 정사각형 혹은 정삼각형 만들기, 도형 내부에 갇힌 공 꺼내기, 건축물 모형의 방향 바꾸기 등[12],[13]이 도형 맞추기에 해당한다.

등식 맞추기 퍼즐 게임의 조건은 “0+3=09” 모양의 배치에서 성냥개비를 옮겨 등식을 만족시키는 것인데, 특히 어린이들의 산술 학습에 도움이 된다[14],[15]. 이 퍼즐 게임은 숫자의 개수와 허용되는 성냥개비의 이동 횟수에 따라 난이도가 달라지므로 성장과정에 알맞게 수준을 조절할 수 있다.

이 논문에서는 등식 맞추기 퍼즐에 대한 해답을 찾는 알고리즘을 구현하고 실험한다. 구현된 알고리즘은 새로운 퍼즐을 고안하는 데에도 활용될 수 있다.

Ⅲ. 성냥개비 등식 퍼즐 개임을 위한 기본 자료구조

3-1 설계 목표

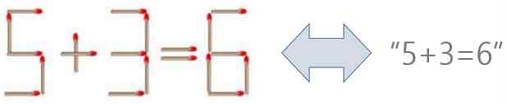
등식 맞추기 성냥개비 퍼즐 게임의 설계 목표는 그림 1과 같이 문자열로 주어진 초기 수식을 성냥개비 배치 저장 구조로 변환한 후, 주어진 개수 이내의 성냥개비를 옮겨 등식이 만족되는 경우가 있는지를 탐색하는 데 있다. 이때, 수식은 성냥개비 배치 저장 구조를 등식 문자열로 변환하여 계산하는 방법이 편리하다. 그림 2에 등식 맞추기 성냥개비 퍼즐 게임의 전체적인 깊이우선 재귀호출 알고리즘을 보였다.

Fig. 1.

Conversion between internal structure of matchstick layout and equation string

Fig. 2.

Rough algorithm for the matchstick equation puzzle game

3-2 성냥개비 숫자 식별 및 배치 표현을 위한 자료구조

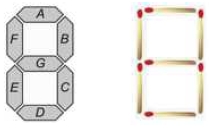
성냥개비를 이용하여 숫자를 표현하는 방법은 그림 3의 7-세그먼트 형식과 동일하다. 그림 4에 7-세그먼트의 각 요소를 ‘0’ ~ ‘9’의 숫자와 ‘+’, ‘-’ 연산자의 모양에 따라 7-세그먼트의 A에서 G까지의 순서로 0~6번 비트에 대응시킨 각각의 비트 패턴 및 이들과 아스키 코드와의 변환 테이블을 위한 구현 코드를 보였다. 여기서 Seg_bit[]는 ‘0’~‘9’, ‘+’, ‘-’에 대한 7-세그먼트 비트 패턴을, Seg_map[]은 7-세그먼트 비트 패턴에 대한 ‘0’~‘9’, ‘+’ ,‘-’을 대응하는 테이블이다.

Fig. 3.

7-segment for digit presentation of matchstick

Fig. 4.

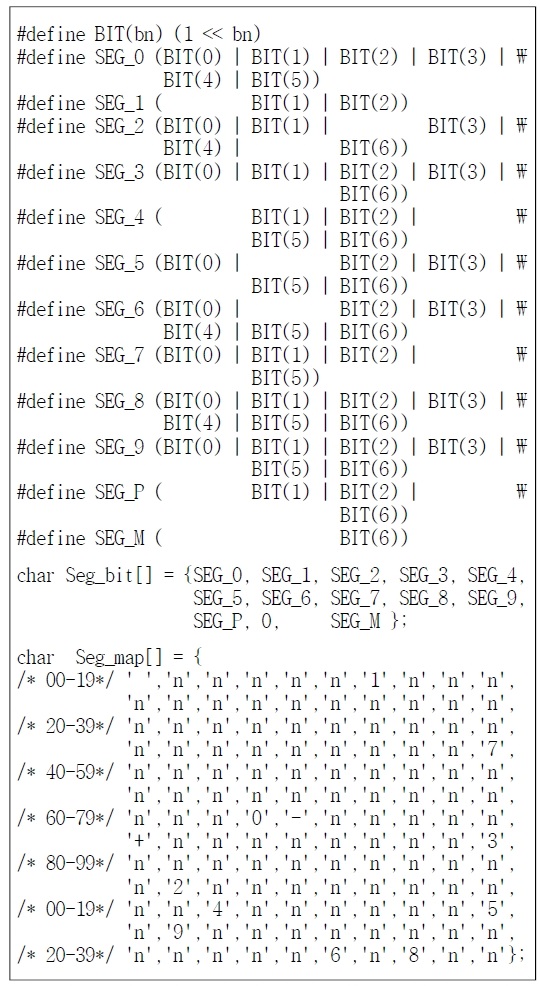
Implemented code for 7-segment bit [attern for digit and operator, and conversion table with ASCII code

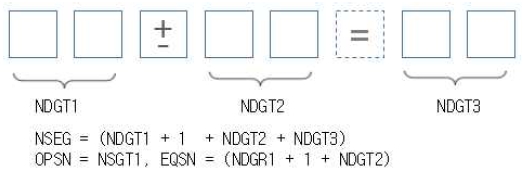
성냥개비 등식 퍼즐 게임의 일반적인 배치는 7-세그먼트를 기반으로 그림 5와 같이 모델링할 수 있고, 이 모델에서 ‘=’을 위한 세그먼트는 실제로 배치할 필요가 없다. 그림 5에 나타난 약어들의 의미는 아래와 같고, 이를 구현한 코드는 그림 6에 보였다. 여기서 Seg_lay[]는 7-세그먼트로 표현되는 성냥개비의 전체 배치를 저장하는 내부 구조이다.

• ∘ NDGT : number of digits
• ∘ NSEG : number of 7-segment for matchstick layout
• ∘ OPSN : segment position of operator symbol
• ∘ EQSN : segment position of equal symbol

Fig. 5.

Modeling for matchstick equation puzzle game layout

Fig. 6.

Implemented code for model of fig. 5

3-3 등식 문자열과 7-세그먼트간 상호 변환 및 출력

초기 등식 문자열은 성냥개비 이동 과정을 추적하기 위해 내부의 7-세그먼트 배치로 변환되어야 한다. 또한, 성냥개비가 이동된 후 등식의 만족 여부를 판단하기 위해서는 7-세그먼트 배치의 내부 구조가 등식 문자열로 변환되어야 한다. 그림 7에 이들 상호간의 변환 프로시저를 보였는데, seg_get() 프로시저는 현재 숫자가 완성되지 않은 상태라면 flase(=0)를 리턴한다. 그림 9는 그림 5의 성냥개비 배치의 내부 저장 내용을 그림 8의 예와 같이 각각의 7-세그먼트를 다섯 줄로 나누어 콘솔 화면에 출력하는 프로시저이다.

Fig. 7.

Procedure for conversion between equation string and 7-segment

Fig. 8.

An example of console output for matchstick layout

Fig. 9.

Procedure for outputting matchstick layout to console

Ⅳ. 성냥개비 등식 퍼즐 탐색 알고리즘

4-1 성냥개비 이동 처리 프로시저

7-세그먼트 ss의 bs 구성 요소(비트)를 세그먼트 sd의 bd 구성 요소로 옮기기 위해서는 아래의 세 가지 절차가 필요하다.

• ∘ ss 세그먼트의 bs 구성 요소가 채워져 있는지 체크한다.
• ∘ sd 세그먼트의 bd 구성 요소가 비어있는지 체크한다.
• ∘ 위 두 가지 사항이 만족한다면 ss 세그먼트의 bs 구성 요소를 비우고, sd 세그먼트의 bd 구성 요소를 채운다.

‘±’의 연산자 세그먼트에 대해서는 특정 구성 요소가 아닌 현재 값을 기준으로 채움과 비움이 결정되어야 하는데, 현재 값이 ‘+’라면 더 이상 받을 수 없는 채움 상태이고, ‘-’이면 하나를 받아 ‘+’가 될 수 있는 비움 상태로 판단한다. 그림 10에 성냥개비의 이동을 처리하는 프로시저를 보였다.

Fig. 10.

Procedure for movement process of matchstick

4-2 성냥개비 등식 퍼즐 탐색 알고리즘

일반적인 게임 트리는 현재 선택 가능한 행동별로 이후에 이루어질 수 있는 가능한 모든 행동 조합들을 경우의 수로 분류하여 이번에 취할 최선의 선택을 제안하는 이잡기식 혹은 완전 알고리즘(exhaustive algorithm, brute-force algorithm)[16],[17] 형태이다. 이잡기식 알고리즘은 미래의 상태 변화가 고정되는 결정론적 게임 트리에서 가능하고, 그 구현 방법은 간단명료하지만 요구되는 메모리 용량이나 계산량이 한계를 넘으면 트리 전체를 전개할 수 없기 때문에 곤란하다. 따라서 대부분의 게임 트리는 주어진 일정 단계까지만 전개하고, 그 시점에서의 승리 가능성에 AI 기법등을 활용하는 평가 함수를 도입한다.

성냥개비 등식 퍼즐 게임에서는 옮기는 성냥개비 개수가 1~3개 정도로 제한되므로 게임 트리를 끝까지 전재할 필요가 없고, 각 단계에서의 평가는 등식의 성립 여부이므로 그림 1에 보였던 결정론적 게임 트리 유형의 적용을 고려할 수 있다. 다만, 성냥개비를 옮긴 후의 새 국면(배치)에서 이전의 국면으로 되돌아가거나 이미 탐색되었던 등식과 중복된 결과를 얻을 수 있다는 점이 다르기 때문에 이에 대한 대응책이 필요하다.

우선, 이전 국면으로 되돌아가는 상황은 다음과 같이 식별할 수 있다.

• ∘ 옮겨 놓은 성냥개비를 또 다른 곳으로 옮기려고 하는 경우
• ∘ 이미 한 번 옮겨서 비어있는 곳으로 옮기려고 하는 경우

이를 위한 방법은 새로운 국면으로 진입하는 과정 즉, 성냥개비의 이동 이력을 스택 구조로 관리하고, 옮기려는 성냥개비의 출발지나 도착지가 스택에 존재하는지를 체크함으로써 가능하다. 그림 11에 성냥개비 이동 과정 추적 및 체크를 위한 trc_*() 프로시저들을 보였다.

Fig. 11.

Procedure for matchstick movement tracking

다음으로, 탐색 결과가 이미 탐색을 마친 등식과 중복되는 지는 아래와 같이 식별할 수 있다.

• ∘ 동일한 이동이지만 순서만 다른 경우
• 　이를테면 a→x, b→>y의 이동 결과는 b→y, a→x의 이동 결과와 동일하다.
• ∘ 이동은 다르지만 결과가 동일한 경우
• 　이를테면 a→x, b→>y의 이동 결과는 a→y, b→x의 이동 결과와 동일하다.

위 두 가지 모두를 체크하는 방법으로, 지금까지 발견된 이동 경로 각각에 대한 출발지점들의 집합 Sk, 도착지점들의 집합 D_k, 이번에 발견된 이동 경로의 출발지점 집합 S, 도착지점 집합 D를 각각 정의하고, “S_k ≡ S and D_k ≡ D ”인 k가 존재하는지를 체크하는 방안을 생각할 수 있다. 그런데, 출발지점 집합과 도착지점 집합이 동일하면 그 결과인 등식도 동일하므로 여기서는 발견된 등식들을 관리하여 비교하는 방법을 적용한다. 그림 12에 탐색 결과의 중복성을 체크하는 seg_new() 프로시저를 보였다.

Fig. 12.

Procedure for checking redundancy of equation

앞에서 언급한 자료구조 및 프로시저들을 기반으로 그림 2의 알고리즘을 구현한 코드를 그림 13에 보였고, 그 개략적인 내용은 다음과 같다.

Fig. 13.

Implemented code for algorithm of Fig. 1

• ∘ 성냥개비 하나를 옮길 때마다 등식 만족 여부를 체크하여 만족하는 경우 그 결과를 출력한다.
• 　- move(), seg_new()
• ∘ 변화된 새 국면으로 내려가 이전 국면에서와 동일한 과정으로 새로운 탐색을 진행한다.
• 　- game_DFS()
• ∘ 새로운 국면으로 내려왔을 때 국면의 깊이가 한계에 다다르면 리턴한다.
• ∘ 이동이 가능한 모든 조합(성냥개비가 놓인 곳의 위치와 비어있는 곳의 위치) 각각을 하나씩 특정한다.
• 　- ss: source segment number
• 　- sb: source bit number in the ss segment.
• 　- ds: destination segment number
• 　- db: destination bit number in the ds segment
• ∘ 특정된 이동 조합에 대하여 위 과정을 반복한다.

4-3 실험 결과

1) 알고리즘 기능

구현된 알고리즘의 기능을 검증하기 위해 시험용 초기 배치(등식) “0+3=09”에 대한 알고리즘의 처리 결과를 분석한다.

• 등식의 중복성 식별

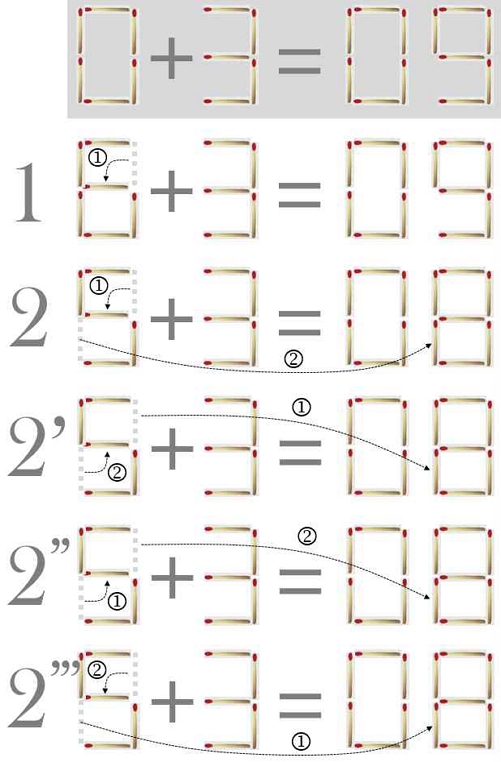
시험용 초기 배치에 대하여 성냥개비 2개까지의 이동으로 등식을 만족시키는 서로 다른 이동 조합은 그림 14와 같다. 이 그림에서 “1”은 한 개의 이동으로 얻은 결과이고, “2”~“2^‘’‘”은 두 개의 이동으로 얻은 결과인데, “2”~“2^‘’‘”은 이동의 순서만 다를 뿐 모두 동일하다. 따라서, 맨 처음 발견된 “2” 외에 나중에 발견된 “2^‘”~“2^‘’‘”은 모두 버려야 한다.

Fig. 14.

Analysis on the solution for the test layout

그림 15에 시험용 배치에 대한 구현 알고리즘의 처리 결과를 보였는데, 그림 14와 일치함을 알 수 있다.

Fig. 15.

Redundancy checking of the implemented algorithm for the found equations

• 이전 국면으로의 회귀 예방

그림 14의 “1”에서, (0, 1) 위치의 성냥개비가 (0, 6)의 위치로 이동된 후, 비어있는 (0, 1) 위치로의 이동이나, 옮겨간 (0, 6) 성냥개비의 다른 곳으로의 이동은 불허되어야 한다. 그림 16에서 구현 알고리즘이 이전 국면으로의 회귀를 예방하는 모습을 볼 수 있다.

Fig. 16.

Skipping situation recognition of the algorithm

2) 알고리즘 시간 복잡도

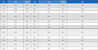
7-세그먼트의 개수를 n(=NSEG)이라 했을 때 구현된 알고리즘은 성냥개비 하나의 이동에 대하여 O(n²)의 복잡도를 가지므로, 성냥개비를 m개 옮기는 경우의 복잡도는 O(n^2m)이다. 이는 NP(Non Polynomial)에 속하는 높은 복잡도로서, 이동 가능한 모든 조합에 대한 탐색을 목표로 하는 이 논문의 범위 안에서는 불가피하다. 구현 알고리즘의 실용성 측면에서의 타당성을 살펴보기 위해 “□±□=□”(Type 1), “□±□=□□”(Type 2), “□□±□□=□□”(Type 3) 등 세 가지 유형별로 모든 가능한 배치에 대하여 성냥개비 두 개의 이동으로 만족하는 등식이 존재하는지에 대한 탐색 시간을 표 1의 환경에서 측정하고 그 결과를 표 2에 보였다. 이 표로부터 구현된 알고리즘의 현실적 활용가치가 있는 것으로 판단할 수 있다.

Table 1.

Experiment Environment

Table 2.

Experiment Results(Number of movements: 2)

Ⅴ. 결론 및 향후 계획

성냥개비 등식 맞추기 퍼즐 게임은 어린이를 포함한 온 가족이 언제 어디서나 즐겁고 편안하게 즐길 수 있는 건전하고 학습 지향적인 게임이다. 이 논문에서 구현된 알고리즘은 성냥개비 등식 맞추기 퍼즐 게임을 즐길 때 주어진 등식 퍼즐 문제에 대한 답이 존재하는지, 존재한다면 또 다른 답은 없는지를 확인하거나 새로운 등식 퍼즐 문제 고안에 아주 유용하게 활용될 것으로 기대된다. 아울러, 향후 계획으로서 구현 알고리즘의 시간적 복잡도 측면에서 개선할 여지가 있는지와 기하학적 모양 맞추기 알고리즘에 대한 연구를 계속 진행할 예정이다.

References

• The Hans India. History of Matchsticks: Know Its Origin and Why Matchboxes Were Made [Internet]. Available: https://www.thehansindia.com/life-style/history-of-matchsticks-know-its-origin-and-why-matchboxes-were-made-794212
• Y. B. Lim, “Thought about Game and Math Through [The Genius],” Newsletter of the Korean Society of Mathematical Education, Vol. 36, No. 6, pp. 44-46, November 2016.
• A. C. Johnson and A. M. Drougas, “Using 'Goldratt's Game' to Introduce Simulation in the Introductory Operations Management Course,” INFORMS Transactions on Education, Vol. 3, No. 1, pp. 20-33, September 2002. [https://doi.org/10.1287/ited.3.1.20]
• E. M. Goldratt and J. Cox, The Goal: A Process of Ongoing Improvement, 3rd ed. Great Barrington: MA, North River Press, 2004.
• C. H. Martin, “A Simulation Based on Goldratt’s Matchstick/Die Game,” Decision Sciences Journal of Innovative Education, Vol. 5, No. 2, pp. 423-429, July 2007. [https://doi.org/10.1111/j.1540-4609.2007.00152.x]
• S. Dhamala, Enhancing Vocabulary of Young Children through the Use of Matchstick Figures and Pictures, Master’s Thesis, Kathmandu, Nepal, Tribhuvan University, September 2023.
• ChosunMedia. The Reason Why the 7.2m ‘Matchstick Eiffel Tower’, Built Over 8 Years, Failed to Enter the Guinness Book of Records [Internet]. Available: https://www.chosun.com/international/international_general/2024/02/06/WALPKESN7JBMDNU7BZVUKYSVKI/, .
• The Herald Economy Report. How Long Did It Take to Create a World Made of Matchsticks? [Internet]. Available: https://mbiz.heraldcorp.com/view.php?ud=20150406000087, .
• Coding Interview: The Matchstick Game [Internet]. Available: https://nestedsoftware.com/2019/03/05/coding-interview-the-matchstick-game-43a8.88358.html, .
• Nested Software. Coding Interview: The Matchstick Game [Internet]. Available: https://www.geeksforgeeks.org/game-of-matchsticks/, .
• Q.-S. Ye, “A Magic Game of Numbers Based Intelligent Properties of VCR: You Don't Know Who I Am,” in Proceedings of 2008 First International Conference on Intelligent Networks and Intelligent Systems, Wuhan, China pp. 400-403, November 2008. [https://doi.org/10.1109/ICINIS.2008.52]
• Maths Week Ireland. Matchstick Puzzles [Internet]. Available: https://www.mathsweek.ie/2023/puzzles-for-all/matchstick-puzzle/, .
• A Magic Classroom. Match Stick Puzzles [Internet]. Available: https://amagicclassroom.com/uploads/3/4/5/2/34528828/matchstick_puzzles.pdf, .
• LogicLike. Matchstick Puzzles with Answers for Kids and Adults [Internet]. Available: https://logiclike.com/en/matchstick-puzzles, .
• MathEasily. MaMath Matchstick Puzzle for TODAY [Internet]. Available: https://matheasily.com/matchstick-puzzles.html, .
• K. Ishihata, Algorithm and Data Structure, J. H. Park and J. G. Kim, trans. Seoul: Hongreung Publishing Company, 1999.
• J. M. Koo, Algorithm Problem Solving Strategies, Seoul, Insight Press, 2012.