회귀 분석을 이용한 청소년 맞춤 메타버스 프로그램 추천

Ⅰ. 서 론

최근 디지털 기술의 혁신적 발전은 가상현실(VR), 증강 현실(AR), 그리고 메타버스(Metaverse)와 같은 새로운 상호작용 기술의 제공을 가능하게 하였다[1]. 이중 메타버스는 게임, 교육, 업무 등 다양한 분야에서 활용되며 그 중요성이 점차 증대되고 있다[2]. 메타버스 기술은 현실과 가상을 넘나드는 다층적 경험을 제공함으로써, 그 가능성이 더욱 확대됨에 따라 청소년들 사이에 빠르게 수용되어 청소년들의 학습과 성장, 사회화 과정에 새로운 기회와 도전을 다양한 방향으로 제시하고 있다[3]. 청소년들 사이에서 메타버스는 새로운 소통의 장을 제공하며, 학습과 여가 활동의 장으로서도 큰 가능성을 내포하고 있다[4]. 이와 같이 청소년들 사이에서 메타버스가 새로운 소셜 미디어 플랫폼과 학습 도구로 부상함에 따라 청소년들이 메타버스를 이용할 경우의 이용 행태를 탐색한 연구도 있다[5]. 또한 한국청소년정책연구원에서는 2022년 메타버스를 활용한 청소년 전국 현신모델 구축방안 연구를 위한 설문 조사[6]를 실시하였으며, 본 연구에서는 연구를 위하여 이 설문자료 중 메타버스를 경험하거나 하지 않은 학생들의 메타버스에 대한 반응과 선호도의 데이터를 수집하였다.

본 연구에서는 메타버스를 경험해본 청소년들의 선호도와 인식을 분석함으로써 메타버스 기술을 더욱 효과적으로 활용할 수 있는 방안을 모색한다. 구체적으로, 회귀 분석[7]을 이용한 청소년 맞춤 메타버스 프로그램 추천 시스템 개발 연구를 제안한다. 먼저, 예측 모델을 생성하기 위하여 데이터 분석을 실시한다. 수집된 데이터에서 결측치와 이상치를 제거하여 분석의 정확도를 높이도록 데이터의 전처리 과정을 거친다. 이 정제된 데이터를 이용하여 분석을 실시한 후 이를 이용하여 메타버스를 경험해본 학생들의 선호도에 기반을 둔 예측 모델을 생성한다. 생성된 모델을 활용하여 메타버스를 경험해보지 않은 학생들이 관심을 가질 만한 메타버스 프로그램을 예측하고 추천한다. 추천한 결과의 정확도는 실제 학생들이 선호하는 프로그램과 추천한 맞춤형 프로그램이 일치하는지 여부를 통해 추천 모델의 유효성을 검증한다.

Ⅱ. 데이터 분석

한국청소년정책연구원의 메타버스 관련 청소년 실태 조사의 자료[6]를 이용하여 초등학교 4학년부터 고등학교 3학년까지 교육 단계별로 메타버스 경험 유무, 활용 분야, 활용 중 불편함의 원인, 선호 프로그램 등을 분석하였다.

2-1 교육 단계별 메타버스 경험 분석

설문자료를 기반으로 메타버스를 얼마나 경험하였는가를 분석하였다. 그 결과는 표 1과 그림 1이다.

Table 1.

Elementary, middle, and high school students' experience with Metaverse

Fig. 1.

Number of students by educational level based on whether they have experienced the Metaverse

표 1과 그림 1에서 Q1의 ‘1’의 값은 메타버스에 대한 경험이 있음을 나타내며, ‘2’의 값은 경험이 없음을 나타낸다. 표 1과 그림 1에서 초등학교, 중학교, 고등학교의 다양한 교육 수준에서 메타버스의 경험유무에 대한 결과는 상이하다는 것을 나타낸다. 초등학교와 고등학교는 메타버스에 대해 경험이 중학교보다 낮았다. 또한, 초등학교는 응답률이 매우 낮았으나 중학생은 응답률이 가장 높았다.

2-2 메타버스 활용 분야 분석

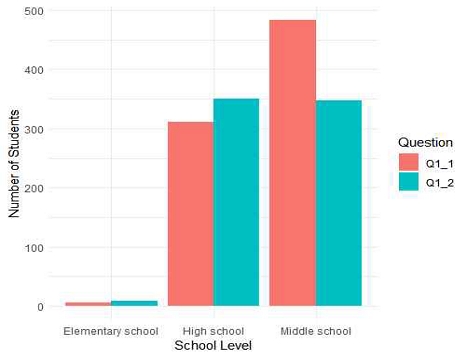
청소년들이 메타버스를 어떤 분야에서 활용하는가를 분석하고자 한다. 표 2는 DM3의 값을 1부터 9까지 정의한다. 이 값은 초등학교 4학년부터 고등학교 3학년까지를 구분하는 코드를 의미한다. 그리고, Q2A1부터 Q2A8까지의 코드는 메타버스를 활용하는 각각의 분야를 나타낸다. Q2A1는 학습, Q2A2는 또래와의 소통과 교류, Q2A3는 창작물의 공유, Q2A4는 정보검색, Q2A5는 개인적 공간 및 아바타 꾸미기, Q2A6는 친구와 대화하는 공간 만들기, Q2A7는 현실에 없는 가상의 공간에 대한 체험, 마지막으로 Q2A8는 가상화폐를 이용한 물건 거래에 이용하는 경우를 나타낸다.

Table 2.

Metaverse applications code for elementary, middle, and high school students

표 3과 그림 2는 학년이 올라감에 따라 청소년들이 Q2A1부터 Q2A8까지 메타버스를 어느 분야에 많이 활용하는가를 분석한 결과이다.

Table 3.

Metaverse usage stats for elementary, middle, and high school students

Fig. 2.

Statistical graph of metaverse utilization by elementary, middle, and high school students

초등학교 4학년은 학습과 현실에 없는 가상의 공간에 대한 체험 항목에서 흥미를 느끼고 있다. 초등학교 6학년은 친구와 대화하는 공간 만들기 항목에 흥미를 보인다. 개인적 공간 및 아바타 꾸미기와 친구와 대화하는 공간 만들기는 중학생과 고등학생들이 가장 많이 활용하는 메타버스 분야임을 알 수 있다.

반면, 고등학교 2학년은 가상화폐를 통한 물건 거래에 흥미가 낮아서 낮은 평균값을 기록하였다. 즉, 고등학생은 아직까지는 가상 화폐를 통한 물품 거래에 대한 관심이나 만족도가 상대적으로 낮음을 알 수 있다. 전반적으로 각 항목별 평균 값은 교육 단계(DM3)에 따라 변화하는 경향을 보이며, 이는 학생들의 관심사와 만족도가 교육 단계에 따라 다르게 나타날 수 있음을 시사한다.

2-3 메타버스 활용 불편한 이유 분석

온라인 활동(줌, 화면공유, 제페토, 로블록스 등)에 참여할 때 불편하다고 느낀 부분에 대해 초등학교 4학년부터 고등학교 3학년들이 표 4의 문항에 대하여 설문한 결과를 분석한다.

Table 4.

Statistics on reasons for inconvenience while using Metaverse

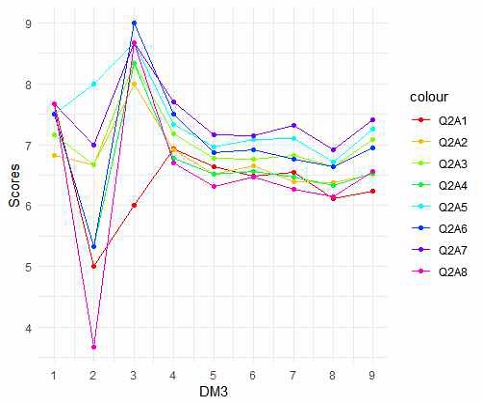
표 4에서 Q6A1는 장비 사용, Q6A2는 컨텐츠 부족, Q6A3은 지도자 역량 부족, Q6A4는 소통 한계, Q6A5는 사생활 노출의 부담감, Q6A6은 친밀감 차이를 나타내는 코드임을 시사한다. 그림 3은 불편하다고 느낀 부분에 대한 통계를 나타낸다.

Fig. 3.

Reasons for inconvenience while using Metaverse Statistical curve

그림 3에서 장비 사용에 대한 불편함은 초등학생에서 고등학생으로 올라갈수록 점차 상승함을 알 수 있다. 학년이 높아질수록 더욱 고가의 장비가 필요하나 이에 대한 공급의 어려움을 나타낸다는 것을 알 수 있다. 콘텐츠 부족의 항목 또한 장비 사용에 대한 불편함과 같이 학년이 올라갈수록 양이 부족하여 불편할 수 있다. 지도자의 역량 부족 역시 학년이 올라갈수록 증가함을 볼 수 있다. 소통의 한계는 다른 항목에 비하여 점차적으로 증가하는 양상을 보인다. 사생활 노출에 대한 두려움은 중학생 이후로 눈에 띄게 증가하며, 나이가 들어갈수록 사생활 노출 문제에 대한 우려 또는 인식이 증가함을 보인다.

온 오프라인의 친밀감 차이 항목에서는 초등학생 4학년에서 가장 높은 점수인 7.25에서 시작하여 학년이 올라갈수록 점점 감소하는 양상을 보인다. 초등학생은 오프라인으로 사람들을 대하는 경우가 많기에 메타버스를 온라인으로 활용할 경우 친밀감이 저하된다는 인식이 있다는 의미를 시사한다. 전반적으로, 불편함의 이유는 초등학생, 중학생, 고등학생이 장비 사용, 콘텐츠 가용성, 리더십 능력, 그리고 소통 등에서 뚜렷한 차이를 나타내지 않는다. 단, 사생활 우려는 주목할만하게 증가함을 볼 수 있다.

2-4 메타버스 선호 프로그램 분석

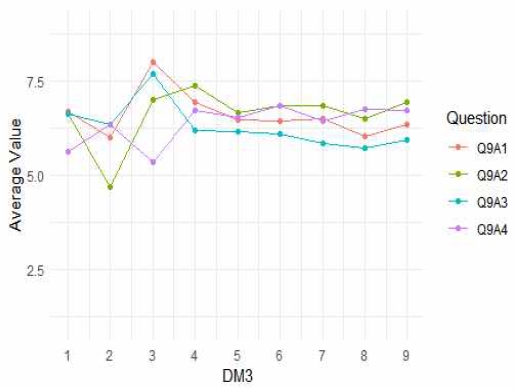
청소년들이 메타버스의 어떤 프로그램을 선호하는가를 분석하고자 한다. 표 5는 선호 프로그램 설문에 대한 코드의 설명이며, 표 6과 그림 4는 학생들이 선호하는 프로그램을 분석한 결과이다.

Table 5.

Metaverse preferred program analysis code

Table 6.

Metaverse preferred program statistics

Fig. 4.

Metaverse preferred program statistical curve

교육 프로그램(Q9A1)은 전반적으로 다른 항목보다 높은 관심을 보였다. 특히 중학생이 경우 가장 높은 관심을 나타냈다. 활동 프로그램(Q9A2)의 점수는 중학교 1학년 때 최고점을 기록했으며, 초등학교 5학년의 경우는 상대적으로 낮은 점수를 기록했다. 이는 활동 프로그램의 경우 시기에 따라 다소 변동성이 있음을 나타낸다. 상담 프로그램(Q9A3)은 초등학교 6학년 때 가장 높은 점수(7.67)를 받았으나 고등학생의 경우 점수가 다소 감소하는 경향을 보였다. 즉, 고학년이 됨에 따라 점차 메타버스를 활용한 상담의 필요성을 느끼지 않았다는 통계를 나타낸다. 융합 프로그램(Q9A4)은 학년에 큰 영향을 받지 않는 비교적 일관된 점수 분포를 보였으며, 중학교 3학년의 경우 최고점(6)을 기록했다.

이 데이터 분석을 통해 각 프로그램의 강점과 약점을 파악할 수 있었으며, 이러한 자료는 프로그램 개선을 위한 기초 자료로 활용될 수 있을 것으로 예상한다.

Ⅲ. 추천을 위한 상관 분석과 회귀 분석

초등학교 4학년부터 고등학교 3학년까지 구분해가면서 분석한 메타버스의 경험유무, 메타버스를 활용하는 분야, 메타버스 사용상 불편함 이유, 메타버스 선호 프로그램의 결과를 기반으로 이들 간의 상관관계를 분석하고 이를 이용하여 예측을 위해 회귀 분석을 실시한다.

3-1 상관 분석

청소년 맞춤 메타버스 프로그램을 추천하기 위해서는 청소년들이 선호하는 프로그램이 메타버스를 활용하는 분야와 메타버스 사용상의 불편한 이유가 어느 정도의 관계가 있는가를 분석하는 것이 필요하다.

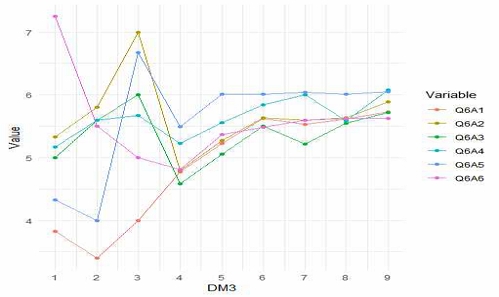
이를 위하여 Q9A1부터 Q9A4의 각 항목과 메타버스를 활용하는 분야, 메타버스 사용상의 불편함 이유 등의 항목들과 상관도를 계산한다. 상관도는 피어슨 상관계수[8]를 이용하여 상관도의 정도를 산출한다. 표 7과 그림 5는 Q9A1부터 Q9A4까지의 프로그램들이 메타버스를 활용하고 있는 분야들과 메타버스 사용 중 불편사항들과 어느 정도의 상관도가 있는가를 나타낸다.

Table 7.

Correlation between Metaverse preferred programs and areas of use and inconveniences

Fig. 5.

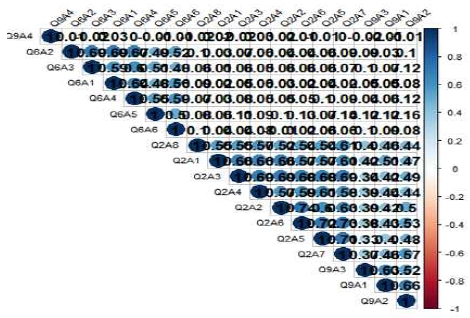
Illustration of correlation between Metaverse preferred programs and areas of use and inconveniences

Q9A1(교육 프로그램)은 Q2A1(0.505)부터 Q2A8(0.457)까지 강한 양의 상관관계를 보여, 변수들 간에 관련성이 높다는 것을 나타낸다. 반면 Q2A1가 Q6A1(0.047)부터 Q6A6(0.092)까지는 상대적으로 약한 상관관계를 나타내며, 이는 교육 프로그램과 이러한 변수들 사이에는 강한 연관성이 없음을 나타낸다. Q9A2(활동 프로그램)는 Q2A6(0.53)과 Q2A7(0.571)와 가장 높은 상관관계를 보이므로, 활동 프로그램이 특히 이 변수들과 밀접한 관련이 있음을 나타낸다. 그러나 활동 프로그램은 Q6A2(0.098)부터 Q6A5(0.16)까지는 상대적으로 약한 상관관계를 보인다. Q9A3(상담 프로그램)은 Q2A1(0.422)부터 Q2A8(0.403)까지 강한 상관관계를 나타내서 상담 프로그램의 평가가 높을수록 이러한 변수들의 평가도 높은 경향을 보이므로 상관도가 높다는 것을 알 수 있다. 반면, 상담 프로그램은 Q6A3(0.095)부터 Q6A6(0.1)까지는 약한 상관관계를 갖는다. Q9A4(융합 프로그램)는 대부분의 변수들과 무의미한 상관관계(-0.02~0.03)를 보여서 융합 프로그램의 평가가 이러한 변수들과는 크게 연관되지 않음을 나타낸다.

종합적으로, Q9A1부터 Q9A4의 각 프로그램은 다른 변수들과 다양한 정도의 상관관계를 갖는다. 교육, 활동, 상담 프로그램(Q9A1, Q9A2, Q9A3)은 Q2A시리즈의 변수들과 중간에서 강한 양의 상관관계를 보이기에 이러한 변수들 사이에 일정한 관계가 있음을 나타낸다.

3-2 회귀 분석

상관 분석을 실시한 결과, Q9A1부터 Q9A4까지 각 프로그램이 Q2A시리즈의 변수들과 강한 선형의 상관도를 나타내므로 이들의 상관관계를 이용하여 선형 학습 모델을 만드는 회귀 분석을 실시한다.

1) 데이터집합

초등학생, 중학생, 고등학생은 이들 단계간의 나이 차이가 크므로 추천을 할 때 데이터를 구분을 하지 않고 진행할 경우 학교 단계별 특성을 반영하지 않아서 추천의 정확도가 낮아진다. 따라서 정확도를 높이기 위하여 학교 단계별로 데이터를 구분하여 회귀 분석을 실시한다. 또한, 메타버스를 경험한 학생들과 메타버스를 경험하지 않은 학생으로 구분하여, 경험한 학생들의 데이터를 기반으로 학습을 실시하고, 경험하지 않은 학생들이 설문한 데이터를 기반으로 테스트를 실시한다. 표 8은 청소년 실태 조사의 설문자료를 기반으로 학습을 위한 훈련집합과 추천을 위한 테스트 집합을 구성한 결과를 나타낸다. 표 9는 메타버스를 경험한 학생들을 대상으로 총 800개의 훈련집합을 구성할 때, 이들 데이터집합 중 3명의 학생을 추출하여 데이터 구성의 예시를 보여준다.

Table 8.

Size of dataset collected by school stage

Table 9.

Example of training set data for students who have experienced Metaverse

2) 선형 회귀 모델 학습

선형 회귀 모델은 예측, 시계열 분석, 인과 관계 추정 등 다양한 분야에서 널리 사용된다[9]. 예를 들어, 기업의 이익을 예측하거나, 광고 비용과 판매량 사이의 관계를 분석하는 데 사용될 수 있다[10],[11].

선형 회귀 분석의 주요 목표는 주어진 데이터에 대해 최적의 β 계수들을 찾아내어 모델의 예측 성능을 최대화하는 것이다. 이 과정에서 종종 최소제곱법(OLS, Ordinary Least Squares)[12]이라는 방법을 사용하여 실제 값과 모델 예측 값 사이의 차이, 즉 제곱 오차의 합을 최소화하는 계수를 찾는다[13].

선형 회귀 모델 학습은 통계학에서 관찰된 연속적인 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하는 과정이다. 이 방법은 변수 간의 선형 관계를 찾아내는 데 사용되며, 주어진 데이터집합에 가장 잘 맞는 선형 방정식을 찾아내는 것을 목표로 한다. 선형 회귀 모델의 기본 선형 방정식 형태는 식 (1)과 같다[14].

$\[ Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots +{\beta }_n{X}_n+ϵ \]$

(1)

식 (1)에서 Y는 종속 변수, X₁, X₂,...,X_n은 독립 변수이고, β₀는 절편이며 β₁, β₂,...,β_n는 각 독립 변수의 계수이다. ε는 오차항이다.

선형 회귀 모델을 이용하여 메타버스 선호 프로그램을 추천하기 위하여 메타버스 활용 분야인 Q2A1부터 Q2A8까지의 데이터를 기반으로 Q9A1부터 Q9A4까지의 값을 예측한다. 이와 같은 선형 회귀 모델은 식 (2)와 같이 정의한다. 식 (2)는 표 8에 있는 형태의 훈련집합에 속한 학생들의 Q2A1부터 Q2A8까지의 값을 기반으로 학습하여 모델링된 Q2Ak_i의 값을 도출하는 식이다.

$\[ Q2A{k}_i={\beta }_{i0}+{\beta }_{i1}{X}_1+{\beta }_{i2}{X}_2+\dots +{\beta }_{i8}{X}_8+{ϵ}_i \]$

(2)

Table 10.

The values of β0, β1, β2,...,βn of the prediction model created separately by school level

식 (2)에서 k_i의 값은 1부터 4까지의 값을 나타내며, 표 8은 학교 단계별로 구분하여 생성한 예측 모델의 β₀, β₁, β₂,...,β_n의 값을 나타낸다.

Ⅳ. 메타버스 맞춤형 프로그램 추천

4-1 선형 회귀 모델을 이용한 메타버스 선호 프로그램 추천

1) 예측을 위한 데이터집합

표 8과 같이 단계별로 구분된 데이터집합 중 메타버스의 경험이 없는, 즉 Q1의 값이 ‘2’인 데이터만을 추출하여 테스트 집합으로 수집한다. 이를 이용하여 메타버스 선호 프로그램을 추천하기 위한 예측을 진행한다. 표 11은 예측을 진행하기 위한 데이터집합 중 3개의 데이터를 추출한 예시를 나타낸다.

Table 11.

Example of test data for making predictions

표 11의 데이터와 같은 형태의 테스트 집합의 총수는 707개이다. 이 데이터를 대상으로 각 학교 단계별로 예측을 진행한다. 표 11에서 ‘?’의 의미는 Q2A1부터 Q2A8의 값을 이용하여 값을 예측을 하여 예측값을 도출하겠다는 의미이다.

2) 메타버스 프로그램의 선호도 예측

테스트 집합의 데이터를 이용하여 식 (2)의 선형 회귀식에 대입을 할 경우, 학생 개개인의 각 메타버스 프로그램에 대한 선호도를 예측할 수 있다. 따라서 표 11의 예시 데이터를 식 (2)의 선형 회귀식에 대입을 하면 표 12와 같이 Q9A1부터 Q9A4의 값을 예측할 수 있다. Q9A1부터 Q9A4의 의미는 표 5에 기술되어 있다.

Table 12.

Predicting values ​​from Q9A1 to Q9A4

3) 선호 메타버스 프로그램 추천

예측값을 기반으로 프로그램을 추천하는 개인화 추천 시스템에서 아마존과 같은 쇼핑몰 등에 사용되는 기법이다. 이와 같은 개인화 추천 시스템을 메타버스 프로그램을 추천하는 방식으로 응용하고자 한다[15]. 기존 개인화 추천 시스템의 경우 사용자가 입력한 선호도를 대상으로 아이템을 추천하는 방식으로 활용하였으나 본 논문에서는 학생들이 입력한 자신의 학습 방향 등을 기반으로 추천에 적용한다.

표 11의 예시 테스트 집합에 있는 한 학생(j)의 Q2A1부터 Q2A8의 값을 식 (2)에 의해 적용하여 이 학생에 대한 Q9A1부터 Q9A4의 값을 표 12와 같이 산출하였다. 이 산출된 값 중 가장 최대의 예측값을 추출한 후 이 값에 해당하는 프로그램이 j라는 학생이 가장 선호할 메타버스 프로그램이라고 지정하여 추천한다. 식 (3)은 j라는 학생의 최대 예측값을 추출하는 식이다.

$\[ { MaxPrediction}_j=\text{max}{\left(Q9A{k}_i\right)}_j\left(1\le i\le 4\right) \]$

(3)

메타버스 선호 프로그램을 추천하는 예를 표 12에 있는 자료를 대상으로 기술하고자 한다. 식 (3)에 고등학생(j=1), 중학생(j=2), 초등학생(j=3)을 각각 적용할 경우, 고등학생(j=1)은 MaxPrediction₁은 7.785372으로 Q9A1를 추천받는다. 그리고 중학생(j=2)의 MaxPrediction₂은 6.0202050으로 Q9A2를 추천받는다. 마지막으로 초등학생(j=3)의 MaxPrediction₃은 5.9047620로 Q9A1를 추천받는다.

4-2 정확도 분석

본 연구에서는 데이터집합을 초등학교, 중학교, 고등학교의 세 가지 교육 단계로 구분하여 회귀 분석을 적용하였고, 또한 개개인의 선호도에 맞추어 맞춤형 메타버스 프로그램을 추천하였다. 이에 대한 추천의 정확도를 분석한다.

테스트 집합의 크기를 n으로 정의하고, n개의 데이터 중 추천이 정확하게 이루어진 데이터의 수를 p로 정한다. 이와 같이 정의된 변수를 이용하여 식 (4)에 적용하여 정확도(Accuracy)를 측정한다[16].

$\[ Accuracy =p/n\times 100 \]$

(4)

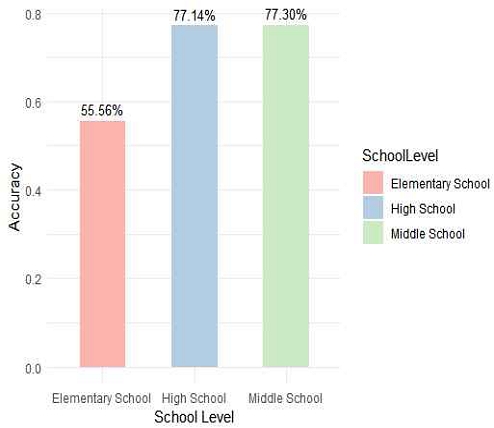
분석 결과, 초등학생 데이터집합의 경우, n = 9이고 p = 5이다. 이 경우의 정확도는 식 (4)에 의해 55.56%이다. 중학생 데이터집합의 경우는 n = 348이고 p = 269이므로, 그 정확도는 77.30%이다. 마지막으로, 고등학생 데이터집합의 경우는 n = 350, p = 270이므로 정확도는 77.14%이다. 그림 6은 이와 같은 결과를 정리한 내용이다.

Fig. 6.

Recommendation accuracy graph by school level

그림 6을 보면 중학생과 고등학생의 데이터집합을 대상으로 한 추천은 그 정확도가 높았다. 그러나 초등학생 데이터집합 대상의 추천은 중학교 고등학교의 데이터집합을 대상으로 하는 추천보다 낮은 정확도를 나타냈다. 이러한 이유는 학습 데이터집합의 크기가 학습 알고리즘의 정확도에 중요한 영향을 미칠 수 있음을 시사한다. 즉, 제한된 데이터 크기로 학습된 알고리즘은 충분히 학습되지 못하는 것으로 해석할 수 있다.

본 연구의 결과는 교육 단계별 학습 알고리즘의 개발 및 적용에 있어 학습할 데이터집합의 크기와 품질이 중요한 고려 요소임을 알 수 있다.

Ⅴ. 결 론

본 연구에서는 메타버스를 경험한 청소년들의 선호도와 인식을 분석하여, 메타버스 기술을 더욱 효과적으로 활용할 수 있도록 회귀 분석을 적용한 청소년 맞춤 메타버스 프로그램 추천 시스템을 제안하였다. 기계학습 알고리즘을 활용하여 메타버스를 경험한 학생들의 선호도에 기반을 두어 예측 모델을 생성하고, 이 모델을 활용하여 메타버스를 경험해보지 않은 학생들이 관심을 가질 만한 메타버스 프로그램을 추천하였다. 추천의 정확도는 초등학생, 중학생, 고등학생 중 고등학생의 정확도가 가장 높았으며, 다음으로 중학생, 초등학생의 순이었다. 초등학생의 경우 사용된 데이터의 크기가 극소로 작아서 이를 기반으로 학습한 결과 추천의 정확도가 낮았다.

본 연구를 통해 개발된 메타버스 맞춤형 프로그램 추천 시스템은 청소년들이 메타버스를 경험하면서 느끼는 흥미와 기대를 반영하여, 개인별 맞춤형 프로그램을 제공함으로써 메타버스 활용의 폭을 넓히는 데 기여할 것으로 기대된다. 이는 메타버스 환경에서의 교육적, 사회적 상호작용을 촉진하고, 청소년들의 창의력과 협업 능력을 강화하는 데 중요한 역할을 할 것이다.

향후, 메타버스의 사용에 대한 초등학생의 자료를 보완하고 메타버스의 사용빈도와 시간 등의 요소를 추가하여 청소년에게 메타버스 프로그램을 추천하는 방법을 적용하는 연구를 하고자한다.

References

• M. Trunfio and S. Rossi, “Advances in Metaverse Investigation: Streams of Research and Future Agenda,” Virtual Worlds, Vol. 1, No. 2, pp. 103-129, October 2022. [https://doi.org/10.3390/virtualworlds1020007]
• A. Rejeb, K. Rejeb, and H. Treiblmaier, “Mapping Metaverse Research: Identifying Future Research Areas Based on Bibliometric and Topic Modeling Techniques,” Information, Vol. 14, No. 7, 356, June 2023. [https://doi.org/10.3390/info14070356]
• G. R. El Said, “Metaverse-Based Learning Opportunities and Challenges: A Phenomenological Metaverse Human-Computer Interaction Study,” Electronics, Vol. 12, No. 6, 1379, March 2023. [https://doi.org/10.3390/electronics12061379]
• E.-Y. Kim, S.-M. Lee, and J.-A. Kang, “Metaverse-Based Career Exploration for Education Students: Approach to Education for Social Responsibility,” Journal of Digital Contents Society, Vol. 25, No. 1, pp. 101-110, January 2024. [https://doi.org/10.9728/dcs.2024.25.1.101]
• S.-H. Park and K.-Y. Kim, “An Exploratory Study on the Usage Behavior of Youth Metaverse Users,” Journal of the Korea Contents Association, Vol. 23, No. 7, pp. 416-427, July 2023. [https://doi.org/10.5392/JKCA.2023.23.07.416]
• National Youth Policy Institute. Study on Building a Youth Policy Innovation Model Using Metaverse [Internet]. Available: https://www.nypi.re.kr/archive/mps/program/examinDataCode/view?menuId=MENU00226&pageNum=1&titleId=168&schType=0&schText=%EB%A9%94%ED%83%80%EB%B2%84%EC%8A%A4&firstCategory=&secondCategory=, .
• A. Field, Discovering Statistics Using IBM SPSS Statistics, 4th ed. London, UK: Sage, 2013.
• J. Hauke and T. Kossowski, “Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Sets of Data,” Quaestiones Geographicae, Vol. 30, No. 2, pp. 87-93, June 2011. [https://doi.org/10.2478/v10117-011-0021-1]
• G. James, D. Witten, T. Hastie, and R. Tibshirani, An Introduction to Statistical Learning, New York, NY: Springer, 2013.
• J. Neter, M. H. Kutner, C. J. Nachtsheim, and W. Wasserman, Applied Linear Statistical Models, Boston, MA: McGraw-Hill, 1996.
• H. Best and C. Wolf (Eds.), The SAGE Handbook of Regression Analysis and Causal Inference, London, UK: Sage, 2015.
• K. S. Hur, “Debt Covenant Hypothesis Verification depending on Management Performance,” Korea International Accounting Review, Vol. 106, pp. 221-245, December 2022. [https://doi.org/10.21073/kiar.2022..106.009]
• S. Kim, Change Point Analysis in Linear Regression Model Using Deep Learning, Master’s Thesis, Kyungpook National University, Daegu, February 2022.
• Y. K. Lee, W.-G. Shin, Y.-C. Ju, H.-M. Hwang, G.-H. Kang, S.-W. Ko, and H.-S. Chang, “Estimation of PV Power Generation by Linear Regression Model Using Voltage and Current Data,” Journal of the Korean Solar Energy Society, Vol. 41, No. 5, pp. 47-58, October 2021. [https://doi.org/10.7836/kses.2021.41.5.047]
• E. Yıldız, C. G. Sen, and E. E. Işık, “A Hyper-Personalized Product Recommendation System Focused on Customer Segmentation: An Application in the Fashion Retail Industry,” Journal of Theoretical and Applied Electronic Commerce Research, Vol. 18, No. 1, pp. 571-596, March 2023. [https://doi.org/10.3390/jtaer18010029]
• T. Bartol, “Thoughtful Use of Diagnostic Testing,” The Nurse Practitioner, Vol. 40, No. 8, pp. 10-12, August 2015. [https://doi.org/10.1097/01.npr.0000470366.64804.35]