Fisher의 선형판별함수와 에이다부스트를 응용한 불완전한 데이터 처리 알고리즘

Ⅰ. 서 론

대부분의 딥러닝 모델에서 네트워크 구조와 초기 상태를 결정하는 문제는 전체 성능에 많은 영향을 주고 있어 이를 위한 많은 연구가 계속되고 있다[1]. 이들 연구에서 여러 분류기를 연합하여 결과를 산출하는 앙상블 기법이 효율적이라는 점에 주목하게 되었다. 앙상블은 배깅(bagging)[2]과 부스팅(boosting)[3]으로 대표되는데, 배깅은 서로 다른 또는 같은 분류기의 학습을 병렬로 결합하고 투표(voting) 기법으로 최종 결과를 결정하는 방법이다[4]. 또한 부스팅은 좋은 성능을 가지는 분류기를 미미한 능력이 있는 많은 수의 약한 분류기(weak classifier)를 직렬로 결합하여 만들 수 있다는 것이다. 이중 가장 일반적인 에이다부스트(adaboost)[5],[6]가 있고, 목적함수의 최저점을 구하기 위해 미분 값을 이용하는 방법을 부스팅에 적용한 Gradient Boosting Machine(GBM)과 GBM에 과적합(overfit)을 방지하기 위한 요소를 추가한 XGBoost(eXtream Gradient Boost) 알고리즘이 있다. 본 논문은 에이다부스트를 이용하는데 이는 학습 데이터를 임의로 샘플링하는 중에 잘못 분류된 사건의 가중치를 증가시켜 약한 분류기가 훈련 사건 집합 안에 분류하기 어려운 사건들에 집중할 수 있도록 하는 과정을 반복적으로 수행한다. 이 특징으로 인해 목적지에 빠르게 수렴한다는 점, 라운드 수를 제외한 별도의 모수가 필요 없다는 점, 약한 분류기에 제약이 없다는 장점을 이용할 수 있다.

불완전한 데이터는 유비쿼터스 환경에서 서로 다른 기기와 수집 환경의 다양화로 인해 일부 속성 또는 속성값이 결손 된 데이터를 말한다. 이러한 데이터는 전체적인 성능저하와 연결되므로 해결하기 위해 주로 결손 데이터를 예측하여 대체하는 여러 알고리즘이 제안되었다. 본 논문은 불완전한 데이터의 결손을 보상하기 위해 Fisher의 선형 판별 함수(FLDF)와 엔트로피를 이용하는 분류기[7],[8]로 이진 트리 형식의 결정트리를 생성하고, 에이다부스트의 약한 분류기로 이용한다. 이 분류기에 절단(pruning) 작업을 추가하여 약한 분류기로 사용한다. FLDF는 다변량 통계의 방법을 기반으로 최적의 투사면을 찾은 다음, 사건들을 이 투사면에 투사하고, 각 투사점들 사이의 엔트로피를 측정해 최적의 분류면을 찾아가는 방식[7]이다. 이 분류기를 불완전한 데이터에 적용하기 위해 학습 데이터를 원-핫 인코딩(One-hot Encoding)과 각 사건에 중요도를 부여할 수 있도록 확장된 데이터 표현을 이용한다. 실험과정을 통해 제안 에이다부스트의 결과와 하나의 완전 결정트리의 결과와 비교하여 앙상블의 결과가 우수함을 보인다.

일반적인 에이다부스트가 ID3, CART 알고리즘을 이용해 결정트리를 구성하여 약한 분류기로 사용한다. 이에 반해 제안 알고리즘은 SVM 계열의 FLDF로 약한 분류기를 구성할 수 있음을 보였다. CART와 ID3는 속성값과 평행한 방향으로 만 분류 평면을 구성하며 결정트리를 완성하는 반면 FLDF는 속성의 기울기와 상관없는 초평면으로 결정트리를 구성한다는 차이가 있다. 앞선 연구에서 FLDF의 결과가 다소 우수함을 확인하였다[7],[8].

2장에서는 본 논문과 관련된 기본적인 앙상블 이론과 FLDF를 사용한 약한 분류기와 데이터 확장기법을 소개한다. 3장에서 본 논문에 도입한 절단 과정과 에이다부스트 과정을 소개한다. 4장의 실험을 통해 제안 방법이 우수함을 비교 결과를 통해 보인다.

Ⅱ. 배 경

2-1 약한 학습기(Weak Learner)

1) FLDF를 이용한 분류기

Fisher의 선형분리함수(FLDF)를 이용하는 분류기[7,8]는 노드당 하나의 분류면(hyperplane : P)을 나타내며, 이 분류면을 기준으로 식 (3)과 같이 패턴(X)을 P^L과 P^L로 분류하는 이진 트리 형식의 결정트리를 형성해 나간다.

(3)

식 (3)에서 분류면은 가중치 벡터(W)와 임계값(T)으로 구성된다. 여기서 가중치 벡터는 식 (4)와 같은 선형분리 함수에 따라 각 패턴들의 투사면(W^TX)을 결정하고, 각 패턴들을 투사면에 투사한 다음, 투사점들의 분포에 식 (5)와 같은 엔트로피를 적용하여 임계값을 구하게 된다.

$\[ \frac{W^{T}BW}{W^{T}VW}=\frac{W^T\left[\sum _i\left(\overline{X_i}-\overline{X}\right){\left(\overline{X_i}-\overline{X}\right)}^T\right]W}{W^T\left[\sum _i\sum _j\left(X_{ij}-{\overline{X}}_i\right){\left(X_{ij}-\overline{X_i}\right)}^T\right]W} \]$

(4)

$\[ H\left\{C|{\delta }^d\right\}=P{L}^{*}H\left(p_1\right)+P{R}^{*}H\left(p_2\right) \]$

(5)

식 (5)의 함수에서 사용된 수식은 다음과 같다.

• PL^* = n₁/(n₁+n₂) PR^* = n₂/(n₁+n₂), n₁(n₂) : 왼/오른쪽 영역으로 분류된 패턴의 수
• H(p_i) = -Σp_ij log₂p_ij　i=1,2(왼/오른쪽), i=1,...,부류의 수
• x_ij= 분류된 각 영역에서 부류 j를 가지는 패턴 수
• p_ij = x_ij/n_i

이 알고리즘의 학습 과정을 단계별로 보면 다음과 같다[7],[8],[10].

• 1. 학습 패턴들을 루트노드에 입력한다.
• 2. 현재의 노드에서 식 (4), (5)을 이용해 W와 T를 구하고 결정트리의 현재 층에 저장한다
• 3. 식 (3)의 분류면에 의해 현재 노드의 학습 데이터가 왼쪽(오른쪽) 패턴으로 분류된다.
• 4. 임의의 노드에서 완전한 분류가 이루어지지 않았으면(부류 수가 2개 이상이면), 분류가 완전히 이루어지지 않은 왼쪽(오른쪽)에 하위 노드를 만든다. 이 노드에 분류되지 않은 패턴들을 입력한 후 2번 과정을 반복한다.

2) 데이터 확장 기법[7],[11]

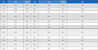
표 1의 훈련 데이터의 예는 3개의 속성과 1개의 부류(Class)로 구성된다. V1과 V3는 {1, 2}를 가지는 2개, V2는 {1, 2, 3}로 구성된 3개, 그리고 부류는 2개의 카디너리티를 가지고 있다. 표 2는 추가로 수집된 데이터이며 일부 속성값이 손실되었다. 이러한 불완전한 데이터의 경우 이를 처리하기 위한 별도의 데이터 구조와 처리를 위한 알고리즘이 필요하다.

Table 1.

The example of learning data

Table 2.

The example of missing data

표 3은 표 1과 표 2가 결합하는 예를 보인다. 우선 표 1의 무손실 데이터는 원-핫 인코딩으로 변환한다. 즉, 해당 엔트리에 {0, 1} 중 하나를 채워 넣는다. 반면 표 2의 손실된 엔트리는 0에서 1사이([0, 1])의 확률적 값으로 채워 넣는다. 여기에 가중치(weight, W) 개념을 더하여 각 레코드를 재정의한다. 가중치 값은 각 사건이 얼마나 중요한지를 나타내는 척도이다. 표 3에서 첫 사건의 가중치가 5라면 이 인스턴스는 5개의 사건과 같은 중요도를 가진다고 할 수 있다. 따라서 에이다부스트 알고리즘에서 다음 학습 데이터를 표본 추출할 때 알고리즘에 의해 가중치의 변환을 반영할 수 있게 한다.

Table 3.

The result of extended data from learning and missing data.

Ⅲ. 불완전한 데이터를 처리하기 위한 에이다부스트

3-2 에이다부스트(Adaboost)

배깅은 학습 데이터 집합에 대해 중복을 허용하면서 각각 다른 학습 데이터로 샘플링 한 후, 이 데이터들을 학습하여 여러 개의 결정트리를 병렬로 구성한 다음, 테스트 데이터를 이들 결정트리에 입력하여 각 결정트리의 결과들을 투표하여 다수결로 가설에 대한 부류를 결정한다. 반면 부스팅은 약한 학습기 여러 개를 결합하여 강한 학습기를 만드는 앙상블 기법인데 이중 가장 널리 사용하는 것이 “adaptive+boosting”을 결합한 에이다부스트[12]-[14]이다. 이는 이전 예측기를 보완하는 새로운 예측기를 만들기 위해 이전 모델에서 오류를 발생시킨 훈련 샘플의 가중치를 높이는 것이다. 즉, 새로 만드는 예측기 모델은 학습하기 어려운 샘플에 점점 더 맞춰 나가는 것이다.

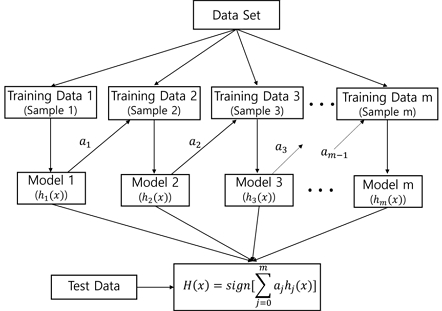
이를 설명하는 것이 그림 1에 나타난다. 우선 데이터를 학습과 테스트 집합으로 분리한 후, 임의로 정한 학습 집합에 FLDF 알고리즘에 절단을 적용한 모델로 학습한다. 이때 오류를 고려한 가중치(a_i)에 따라 샘플링하여 새로운 학습 집합을 구성하고 모델을 통해 새로운 가설(h_i (x))을 세우는 과정을 정해진 수(m)만큼 반복한다. 그리고 테스트 사건을 m 개의 모델에 입력하고 여기에 가중치의 영향을 더하여 최종 결과를 산출한다.

Fig. 1.

The learning procesure of Adaboost

본 논문에서 사용한 에이다부스트의 구체적인 설명은 다음과 같다.

우선, $$ \left(x_1,y_1\right),\dots ,\left(x_n,y_n\right),x_i\in X,y_i\in Y=\left\{-1,+1\right\}$$에 대해 다음과 같이 정의한다.

• • n : 학습 데이터 개수
• • m : 분류기 개수(number of classifiers)
• • h_j (x) : 모델(model) 또는 분류기(classifier)
• • I(A) : 지표함수(Indicator function)
  　　IF(A = True) Return (1)
  　　ELSE Return
• • L_j : 에러 함수(weighted error function)

정의된 기호로 부터 알고리즘은 단계별로 다음과 같이 전개된다.

초기화 과정 :

1. Set initial weight W_i = 1/n, i = 1,...n

학습 과정 :

2. For j=1 to m

Step 1 : Find h_j(x) that minimizes L_j.

$\[ L_j=\frac{\sum _{i=1}^n{W}_{i}I\left(y_i\ne h_j\left(x\right)\right)}{\sum _{i=1}^n{W}_i} \]$

(7)

Step 2 : Define the weight of a classifier.

$\[ a_j=\mathrm{l}\mathrm{o}\mathrm{g}\frac{\left(1-L_j\right)}{L_j} \]$

(8)

Step 3 : Update weight

$\[ W_{t+1}\left(i\right)\begin{array}{l}=\frac{W_t\left(i\right)}{Z_t}\times \left\{\begin{array}{cc}{e}^{-a_{j}t},& \text{if }\left(h_t\left(x\right)=y_i\right)\\ e^{a,t},& \text{if }\left(h_t\left(x\right)\ne y_i\right)\end{array}\right.\\ =\frac{W_t\left(i\right)\mathrm{e}\mathrm{x}\mathrm{p}\left\{a_j{y}_i{h}_t\left(x_i\right)\right\}}{Z_t}\end{array} \]$

(9)

Endfor

출력 과정 :

3. Final boosted model

$\[ H\left(x\right)=sign\left[\sum _{i=1}^m{a}_j{h}_j\left(x\right)\right] \]$

(10)

식 (7)은 L_j = 틀린수/전체로 틀린 비율을 의미한다. 식 (8) 은 분류기의 가중치를 결정하는 것으로 다음으로 설명된다.

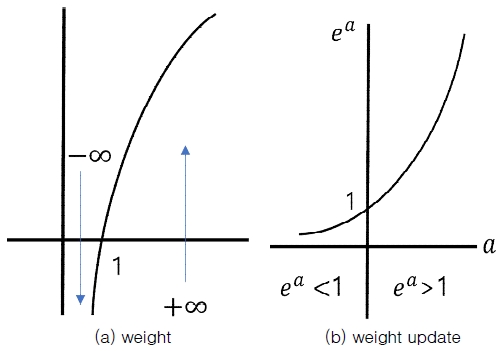
• IF L_j = 0(오류가 없는) $$ a_j=\mathrm{l}\mathrm{o}\mathrm{g}\frac{1}{0}=\mathrm{\infty }$$
• (그림 2의 (a) 로그 그래프에서 +∞ 쪽에 해당)
• ELSEIF L_j = 0.5(헛갈리는) $$ a_j=\frac{1-0.5}{0.5}=\mathrm{l}\mathrm{o}\mathrm{g}1=0$$
• ELSE L_j = 1(전부 틀리는) $$ a_{j }=\mathrm{l}\mathrm{o}\mathrm{g}\frac{0}{1}=-\mathrm{\infty }$$
• (그림 2의 (a)에서 [0,1] 구간에 해당)

Fig. 2.

Weights and weight update rates

식 (9)는 그림 2 (b)의 exp 그래프에서 식 (11)의 성질을 확인할 수 있다.

(11)

다시 말해 가중치(a)가 0보다 크면 가중치 변화량(e^a)을 1보다 크게 한다. 반면에 0보다 작으면 가중치 변화량(e^a)을 1보다 작게 한다. 여기서 z_t는 가중치를 [0,1] 구간으로 만들기 위한 정규화 요소이다. 식 (10)은 최종 판정을 위해 가중치를 고려하는 각 분류기의 결과를 하나로 합치는 것을 의미한다.

Ⅳ. 구 현

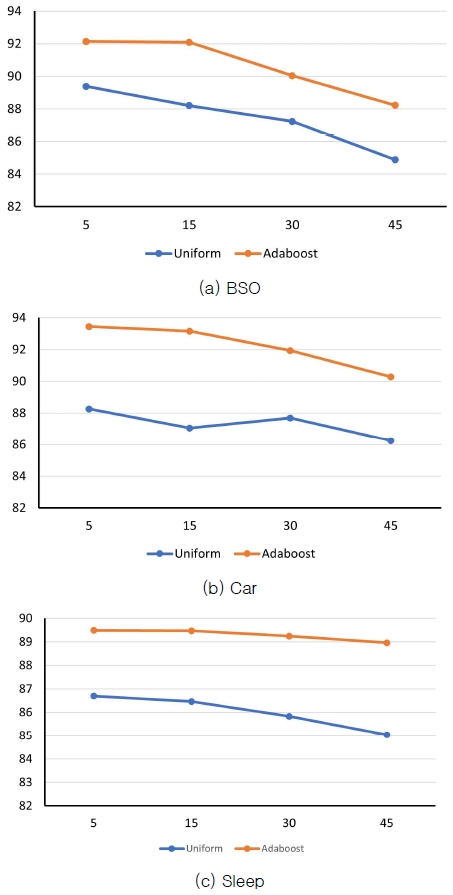
실험에 사용된 데이터는 UCI 기계 저장소[15]에서 “Balance Scale Weight & Distance Database (BSO)”와 “Car Evaluation Database(Car)”를, 그리고 “Sleep stage scoring data set(Sleep)”를 사용하였다. BSO는 625개 사건 (3 변수, 3 부류)을, Car는 1728개 사건(6 변수, 4 부류)을 가진다. 그리고 Sleep은 799개 사건(11 변수, 6 부류)을 가진다. 각 데이터에는 10-겹 교차 검증 방법을 적용하여 결과를 산출하였다. 즉, 전체 데이터 집합을 임의로 10개 블록으로 나누고 교대로 9개는 실험에 하나는 테스트로 사용한 후, 실험 결과의 평균을 산출한다. 이 결과가 표 4에 나타나 있다. 실험은 12개로 고정된 약한 분류기 상에서 손실률(Prun_Rate)을 각 변수당 5%, 15%, 30%, 45%씩 증가하면서 실행하였다. 3.1절에서 식 (6)에 소개되었던 두 절단 방법을 사용한 결과에는 커다란 차이가 나지 않는 것을 확인했으며 표 4의 실험은 식 (6)에서 (a) 식을 사용한 결과이다.

Table 4.

Experiment results

제안 시스템의 결과를 비교하기 위해 2.2절에서 소개한 데이터 확장기법으로 손실 데이터를 형식을 변경한 후 FLDF을 이 데이터에 맞게 변형한 분류기로 학습한 결과와 같은 데이터로 실험하여 비교하였다. 즉 이 분류기는 완전한 결정트리 하나로만 산출한 결과(표 4에서 흰색)이고, 제안 결과는 약한 분류기로 분류한 여러 개의 결정트리와 가중치로 에이다부스트 알고리즘으로 산출한 결과(표 4에서 음영색)이다. 실험한 전체 데이터에서 에이다부스트의 결과가 우수한 것으로 나타났고 이를 명확하게 표시하고자 각 손실률 별로 결과의 평균값을 그래프로 비교한 것이 그림 3에 나타나 있다. 여기서 “Uniform”이 하나의 분류기로 결정트리로 산출한 결과이고, “Adaboost”가 약한 분류기 여러 개가 연합하여 산출한 결과이다. 결과들에서 보듯이 에이다부스트의 결과가 우수한 것을 확인할 수 있으며 이는 앙상블 기법을 사용한 결과로 생각할 수 있다. 다시 말해 앙상블의 이론에서 말하는 바와 같이 하나의 완벽한 결정트리(강한 분류기)보다는 다수개의 미미한 성능을 가지는 결정트리(약한 분류기)를 결합하여 투표를 한 결과가 성능면에서 앞선다는 것을 확인하는 결과라 할 수 있다.

Fig. 3.

Comparison of results in Table 4

Ⅴ. 결 론

지금까지 본 논문은 앙상블 기법 중에 에이다부스트를 이용하는 과정을 살펴보았다. 여기서 약한 분류기로 FLDF에 절단 알고리즘을 적용해 사용하였고 실험 과정에서 강한 학습기인 단일 결정트리의 결과보다는 우수한 결과를 보임을 확인하였다.

그동안 에이다부스트는 여러 분야에서 다양한 문제에 적용하여 성능 개선을 위해 이용되어왔다. 그러나 학습 데이터의 수가 충분하지 못하거나, 학습 데이터에 많은 노이즈나 손실이 있는 경우 등에서 불완전한 결과가 산출될 수 있음을 많은 연구자들이 지적하였다. 이에 대해 약한 학습기가 또 다른 약한 학습기로 정보를 전이하는 과정에서 알고리즘적인 보완이 뒤따라야 할 것으로 본다. 그리고 차기 연구로는 요즘 여러 응용 분야에서 주목을 받고 있는 GBM과 XGBoost를 불완전한 데이터 처리 문제에 이용하는 방안에 대해 고려하고 있다. 물론 정통 딥러닝보다는 관심의 정도가 약하더라도 결과를 서로 비교할 수 있을 정도로 우수하므로 연구할 만한 충분한 가치가 있을 것으로 본다.

Acknowledgments

본 논문은 청운대학교의 2023학년도 학술연구조성비(학술 2023-47)에서 지원을 받았음.

References

• M. Kantardzic, Data Mining: Concepts, Models, Methods, and Algorithms, Hoboken, NJ: Wiley-IEEE Press, 2002.
• L. Breiman, “Bagging Predictors,” Machine Learning, Vol. 24, No. 2, pp. 123-140, August 1996. [https://doi.org/10.1007/bf00058655]
• Y. Freund and R. E. Schapire, “Experiments with a New Boosting Algorithm,” in Proceedings of the 13th International Conference on Machine Learning (ICML ’96), Bari, Italy, pp. 148-156, July 1996.
• T. G. Dietterich, “An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization,” Machine Learning, Vol. 40, No. 2, pp. 139-157, August 2000. [https://doi.org/10.1023/a:1007607513941]
• N. Cristianini and J. Shawe-Taylor, An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods, Cambridge, UK: Cambridge University Press, 2000.
• X. Li, L. Wang, and E. Sung, “A Study of AdaBoost with SVM Based Weak Learners,” in Proceedings of 2005 IEEE International Joint Conference on Neural Networks, Montreal, Canada, pp. 196-201, July-August 2005. [https://doi.org/10.1109/IJCNN.2005.1555829]
• J. C. Lee, D.-H. Seo, C.-H. Song, and W. D. Lee, “FLDF Based Decision Tree Using Extended Data Expression,” in Proceedings of 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, pp. 3478-3483, August 2007. [https://doi.org/10.1109/ICMLC.2007.4370749]
• J. C. Lee, “Application Examples Applying Extended Data Expression Technique to Classification Problems,” Journal of the Korea Convergence Society, Vol. 9, No. 12, pp. 9-15, December 2018. [https://doi.org/10.15207/JKCS.2018.9.12.009]
• R. Polikar, L. Udpa, S. S. Udpa, and V. Honavar, “Learn++: An Incremental Learning Algorithm for Supervised Neural Network,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), Vol. 31, No. 4, pp. 497-508, November 2001. [https://doi.org/10.1109/5326.983933]
• J. C. Lee, “Algorithm to Handling Incomplete Data from Decision Tree Using SVM,” Journal of Knowledge Information Technology and Systems, Vol. 17, No. 6, pp. 1145-1153, December 2022. [https://doi.org/10.34163/JKITS.2022.17.6.006]
• A. Géron, Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow, 2nd ed. Sebastopol, CA: O’Reilly, 2019.
• H. Schwenk and Y. Bengio, “Boosting Neural Networks,” Neural Computation, Vol. 12, No. 8, pp. 1869-1887, August 2000. [https://doi.org/10.1162/089976600300015178]
• T. Chen and C. Guestrin, “XGBoost: A Scalable Tree Boosting System,” in Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco: CA, pp. 785-794, August 2016. [https://doi.org/10.1145/2939672.2939785]
• R. J. A. Little and D. B. Rubin, Statistical Analysis with Missing Data, 2nd ed. Hoboken, NJ: John Wiley & Sons, 2002.
• UCI Machine Learning Repository. Datasets [Internet]. Available: https://archive.ics.uci.edu/datasets