다중 카메라 기반 시선 추적 데이터세트의 기하 정보 추정 기법
Copyright ⓒ 2023 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
인간의 시선을 추적하는 인공지능 기술이 점차 많은 곳에 응용되면서 시선 추적과 관련된 데이터세트의 활용 범위가 점차 넓어지고 있다. 인공지능 시선 추적 기술은 한 사람의 시선 추적에만 머무르지 않고 여러 카메라를 활용하여 특정한 공간 내에서 활동하는 여러 사람들의 시선을 추적하는 문제로 확장되고 있다. 그러나 공개된 대부분의 시선 추적 데이터세트에는 특정한 목적에 집중된 정보만이 제공되어 시선 추적 기술이 다양한 분야로 응용될 수 있는 가능성을 제약하고 있다. 본 논문에서는 다중 카메라를 사용하는 대표적인 시선 추적 데이터세트에서 응용을 위한 3차원 기하 정보를 추출하는 방법을 논의한다. 제시하는 방법을 통해 시선 추적 데이터가 측정되었던 현장의 세부적인 기하 정보를 유도한다. 또한 여러 카메라를 사용할 경우 3차원 공간 정보의 재구성에서의 문제를 논의하고 그 해결책을 제안한다.
Abstract
As artificial intelligence technology that tracks human gaze is applied to increasingly more fields, the scope of use of datasets related to gaze tracking is gradually expanding. Artificial intelligence eye tracking technology is expanding beyond simply tracking the gaze of a single person to tracking the gazes of multiple people active in a specific space using multiple cameras. However, most publicly available eye-tracking datasets provide only information focused on specific purposes, limiting the possibility of eye-tracking technology being applied to various fields. This paper discusses a method to extract 3D geometric information for applications from a representative eye tracking dataset using multiple cameras. Through the presented method, detailed geometric information of the site where eye tracking data was measured is derived. Additionally, problems in reconstructing 3D spatial information when using multiple cameras are discussed and solutions are proposed.
Keywords:
Gaze Estimation, Datasets, Geometry Information, Epipolar Geometry, Artificial Intelligence키워드:
시선 추적, 데이터세트, 기하 정보, Epipolar 기하학, 인공지능Ⅰ. 서 론
1-1 연구 배경
인공지능 연구의 중요성에 대한 공감대가 확산되면서 다양한 데이터세트들이 개발, 공개, 이용됨으로써 인공지능 분야의 발전이 가속화되고 있다. 이러한 데이터세트들은 대학 등의 교육 기관에서 프로젝트의 일부로서 확보, 공개되기도 하고 정부 등 공공기관에서 자금을 투입하여 공익적인 목적으로 공개, 활용되기도 한다[1].
그러나 이러한 공개 데이터세트들은 데이터 수집 환경 등과 같이 실제 적용을 위해 꼭 필요한 메타(meta) 데이터가 누락되어 그 응용 범위가 제한적인 경우가 빈번하다.
본 논문에서는 이러한 공개 데이터세트들 중 하나인 시선 추적용 ETH-XGaze 데이트세트[2]에서 이러한 메타 데이터를 추정하는 기술을 논의한다. ETH-XGaze 데이터세트는 인공지능 기반 시선 추적 학습을 위해 여러 대의 고해상도 카메라를 사용하여 전방 화면의 특정 2차원 지점을 피실험자가 바라보는 모습을 촬영한 이미지와 해당 2차원 지점의 데이터 등을 제공한다.
그러나 이 데이터세트에서는 전방 화면의 크기나 카메라들의 실제 위치 등 결정적인 정보를 관련 논문[3]이나 데이터세트에서 제공하지 않아서 데이터세트의 활용 가능성을 제한하는 측면이 있다.
본 논문에서는 제공된 이미지 데이터세트만으로 실제 구현에 필요한 화면 크기, 화면 좌표, 카메라의 정확한 위치 등 여러 기하 정보들을 추정하는 방법을 논의하고 실제 데이터에 적용함으로써 제안하는 기법의 유용성을 증명한다. 이렇게 추정된 방법을 바탕으로 상업 및 공공시설 등에서 세 대 이상의 다중 카메라들을 이용해서 3차원 정보를 획득하는 알고리즘과 그 결과도 제시한다.
1-2 관련연구
일반적인 카메라는 투사(projection)를 통해 3차원 공간상의 피사체를 2차원 이미지로 변환하는 장치로 볼 수 있다. 이 투사 과정 중 차원 하나가 감소함에 따라 관련된 기하 정보들, 특히 카메라 시선 방향 상에 위치한 3차원 공간의 정보들이 소실된다. 따라서 이 투사의 결과로 생성된 2차원 정보(이미지)만으로 소실된 차원의 정보를 재구성하기 위해서는 추가적인 정보가 필수적이다. 따라서 부족한 정보를 확보하기 위해서는 카메라 한 대로는 불가능하며 두 대 또는 그 이상의 카메라가 필수적이다.
이렇게 두 대의 스테레오 카메라를 구성해서 3차원 정보를 취득하기 위해서는 epipolar geometry[4]를 이용하는 것이 일반적이다. 일반적으로 epipolar geometry는 동일한 카메라 두 대를 사용하는 것이 일반적이나 서로 다른 두 유형의 카메라(RGB와 적외선(IR))를 사용하는 경우에 대한 연구[5]도 발표된 바 있다.
또한 최근 Amazon Go 등과 같이, 상업 시설에서 무인화 기술이 도입됨에 따라 여러 카메라를 이용해서 공간 내 사람들의 3차원 정보를 추출하기 위해 3대 이상의 카메라를 사용하는 경우도 빈번하다. 카메라 2대만 있으면 3차원 정보를 추출할 수 있으나 3대 이상을 사용할 경우 카메라 매개변수에 내재되어 있는 오류를 상쇄시키고 보다 정확한 위치 계산이 가능하다는 장점이 있다. 본 논문에서는 세 대 이상의 카메라를 사용할 때 합리적으로 사람의 특징점(landmark)의 3차원 위치를 추정하는 방식을 유도하고 그 결과를 제시한다.
다중 카메라 기술은 공간 내에서 여러 물체들을 추적하는 용도로 사용[6]된다. 이 응용 분야에서는 기술적으로 다양한 어려움들이 존재하며 이러한 어려움들을 극복하기 위한 여러 가지 방법들이 제안되었다.
여러 카메라에서 포착한 물체가 카메라마다 다른 모습으로 제시되는 것이 일반적이며 이러한 한계를 극복하고 동일한 물체로 인식해야 하며[7], 카메라의 광학적 특성으로 인한 차이로 인해 각 카메라에 포착된 물체의 크기, 색상 등이 달라 추적 상의 어려움[8]이 발생할 수도 있으며, 물체의 다양한 움직임으로 인해 추적이 어려운 문제들도 고려해야 한다. 또한 여러 카메라가 움직일 때 물체를 추적해야 하는 상황에서도 기술적인 난제가 발생한다. 또한 카메라와 목표물의 개수를 알 수 없을 때 발생하는 어려움 등을 해결하는 방안[9]이 제안되었다. 최근에는 이러한 문제들을 해결하기 위해서 딥러닝[10] 등의 다양한 기법들이 제안되었다.
1인칭 시선 추적 기술은 스마트폰이나 태블릿 등과 같은 모바일 기기의 전면 카메라를 이용해서 사용자의 얼굴 이미지를 획득하고 이 이미지를 기반으로 현재 사용자가 모바일 기기 화면 내에서 어떤 지점을 보고 있는지 추정하는 기술이다. 1인칭 시선 추적 기술은 인간 눈의 기하학적인 구조와 광학적인 특성을 고려해서 시선 지점을 추정하는 모델 기반 방식(model-based method)과 사용자의 얼굴 이미지를 인공신경망에 학습시켜서 시선 지점을 추정하는 외형 기반 방식(appearance-based method)으로 나눌 수 있다[11]. 모델 기반 방식은 외형 기반 방식에 비해서 보다 정밀하게 눈의 현재 모습을 획득할 필요가 있기 때문에 적외선 조명 및 적외선 카메라 등이 설치된 추가적인 헤드마운트 장비가 필요한 것이 일반적인 반면, 외형 기반 방식은 추가적인 전문 장비 없이 일반적인 모바일 장치만 필요하며 시선 추적 기술이 사용자의 일상적인 사용 경험을 방해하지 않기 때문에 외형 기반 방식의 적용이 점차 확대되고 있다.
외형 기반 방식은 인공지능 기반 기술이기 때문에 방대한 학습 데이터가 필요하며 이 학습 데이터는 사용자가 모바일 기기의 화면 또는 기타 대형 디스플레이 상에서 특정 지점을 바라보고 있는 이미지와 응시하는 지점의 위치 등이 포함된다. 그러나 시선 추적 기술의 개선을 위해서는 데이터 생성 당시의 여러 기하학적인 정보들이 필요한 경우가 빈번하게 발생하지만, 이러한 정보들은 공개되는 데이터에 누락되는 경우가 일반적이다. 따라서 본 연구에서는 특정 데이터세트에서 데이터 수집 당시의 정확한 환경을 재구성할 수 있는 정보(예. 스크린 배치, 크기, 피실험자 얼굴의 특징점(landmark)의 3차원 위치 등)를 추정하는 방법을 논의한다.
3인칭 시선 추적은 모바일 기기 1대로 한 명의 사용자의 시선을 추적하는 1인칭 시선 추적 기술과는 달리, 한정된 공간 내에 설치된 세 대 이상의 여러 대의 카메라를 이용해서 해당 공간 내에서 활동하고 있는 여러 사람들이 어떤 대상을 보고 있는지 추정하는 기술이다[12],[13]. 이 경우 대상 공간 내에서 사람들의 위치는 물론 사물의 위치도 수시로 변하기 때문에 카메라의 사각 지대를 보완해서 공간 전체의 정보를 획득할 필요가 있다. 따라서 보통 여러 대의 카메라를 사용하며 앞서 논의했던 여러 대의 카메라를 사용하여 공간정보를 획득하는 과정이 필수적이다. 또한 시선 정보가 mm 단위의 정밀도로 추정이 가능한 1인칭 시선 추적 기술과는 달리 공간 내의 사물들 중 어떤 사물을 보고 있는지를 파악하는 것이 일반적이다.
본 논문에서 다루는 ETH-XGaze 데이터세트는 1인칭 시선 추적에 필요한 정보에만 집중하고 있고 여러 대의 카메라를 사용함으로써 3인칭 시선 추적 연구에 활용이 가능한 잠재력을 가지고 있음에도 불구하고 3차원 시선 추적 및 기타 응용에 필요한 여러 3차원 기하 정보들이 명시적으로 제공되지는 않는다. 따라서 본 논문에서 제시하는 방법을 통해 이 데이터세트가 3인칭 시선 추적을 포함한 보다 넓은 분야에 다양하게 응용될 수 있으리라 기대한다.
Ⅱ. 본 론
2-1 ETH-XGaze 데이터세트의 특성과 한계
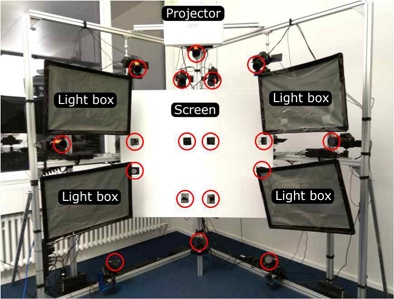
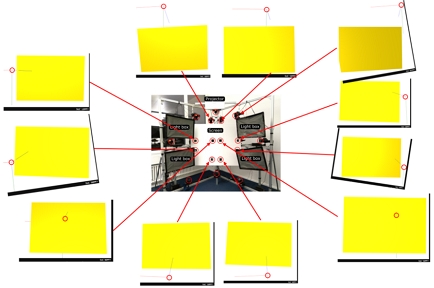
ETH-XGaze 데이터세트[2]는 ETH Zurich에서 시선 추적 및 시선과 관련된 연구를 수행하기 위한 목적으로 제공하는 대규모 데이터세트이다. 이 데이터세트에는 18대의 SLR 카메라와 전면 화면, 프로젝터, 조명 장치 등이 설치된 환경(그림 1)에서 110명의 참가자들이 여러 조명 조건에서 화면에 제시된 지점을 응시하는 장면을 다양한 카메라 각도에서 촬영한 고해상도 이미지들(6000×4000 픽셀)과 관련 메타 정보들이 포함된다. 실험 참가자들은 해당 논문[3]의 Fig. 1에서 제시된 것처럼, 목을 지지대에 고정시킨 상태에서 조명 장치(light box)로 다양한 조명 환경에서 전면 화면 위에 프로젝터로 투사한 지점을 응시하고 이 상황을 동시에 다양한 위치에 설치된 SLR 카메라(그림 1에서 빨간색 원으로 표시)로 촬영하였다. 데이터세트와 함께 제공되는 Readme 파일에서는 데이터세트 내 폴더 구조와 해당 폴더에 포함된 정보들을 설명하고 있다. 기본적으로 이 데이터세트에서는 시선 정보의 학습(train), 테스트(test)를 수행하기 위한 이미지들의 위치 및 파일 이름, 그리고 각 이미지를 촬영할 당시 피실험자들이 바라보고 있는 화면의 2차원 좌표, 각 카메라에서의 머리 위치 및 회전 각도, 얼굴의 2차원 랜드마크(landmark) 정보, 각 카메라의 매개변수 등을 포함하고 있다. 표 1에서는 기준이 되는 첫 번째 카메라(Cam00)에 대한 정보를 제시한다. 그러나 이러한 정보 이외에 실제로 3인칭 시선 추적 및 공간 기하 정보 추적 등과 같은 여러 연구에 데이터세트를 활용하기 위해 필요한 다음과 같은 정보들이 누락되어 있으며, 제공되는 정보들 중 일부도 불명확한 측면이 있다.
피실험자들이 관찰하는 화면(screen)에 투사되는 지점은 화면 좌표 시스템(2차원 정수 좌표)으로만 제공되며 프로젝터의 해상도 정보가 누락되어 있다. 따라서 실제로 피실험자들이 3차원 공간에서 어떤 점을 응시하고 있는지 바로 파악하기가 어렵다.
또한 프로젝터와 화면 정보와 관련해서 화면의 실제 물리적 크기에 대한 정보도 제공되지 않는다. 프로젝터로 영상이 화면에 투사되는 면적이 더 중요하기 때문에 물리적 화면 크기보다는 프로젝터로 투사되는 직사각형 영상 영역의 3차원 정보(즉, 네 모서리 지점의 3차원 정보)를 구할 필요가 있다. 특히 직물 재질로 된 프로젝터 화면의 특징 때문에 배치된 화면이 완전한 평면을 이루지 않고 어느 정도 굴곡 또는 비틀림이 있을 가능성이 있다. 이러한 굴곡이나 비틀림으로 인해 메타 데이터로 제공되는 피실험자들의 2차원 시선 위치 정보를 정확하게 3차원 정보로 재구성 중 어느 정도 오차가 발생한다.
이 데이터세트에는 피실험자들의 얼굴 이미지 위 랜드마크 좌표 정보가 함께 제공된다. 그러나 실제로 이 위치를 이미지 위에 표시해 보면(그림 7 왼쪽) 특정 랜드마크들, 특히 눈 주변의 랜드마크 위치의 정밀도가 현저하게 떨어진다. 이 데이터세트의 주요한 목적 중 하나가 시선 정보 추적이기 때문에 눈 주변의 랜드마크 위치 오차는 이 데이터세트로 학습을 시킨 인공지능 기반 시선 추적 기술의 성능에 큰 영향을 미칠 수밖에 없다.
이 데이터세트에 참여한 피실험자들이 실제로 3차원 공간 내에서 어떤 위치에 있었는지도 바로 파악이 어렵다. 따라서 3인칭 시선 추적 등에서 필수적인 피실험자들의 3차원 기하 정보를 효과적으로 추정할 수 있는 방법도 필요하다.
다음 절에서는 이러한 한계를 극복하기 위해 주어진 정보에서 실험 공간의 기하 정보를 재구성하고 실제 실험자들이 어떤 곳을 바라보고 있는지를 분석하는 방법을 제안한다.
2-2 기하 정보 분석
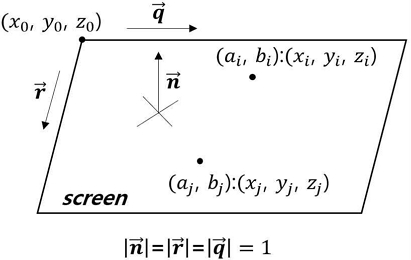
ETH-XGaze 데이터세트에서 화면의 3차원 기하 정보를 파악하기 위해서 이용할 수 있는 정보는 화면의 2차원 픽셀 좌표 (ai,bi)와 해당 지점에 대한 Cam00의 카메라 좌표 기준 3차원 좌표 (xi,yi,zi)이다(그림 2). 또한 2차원 픽셀 좌표 (ai,bi)는 논문이나 데이터세트에는 별도로 명시되지 않았지만 전체 데이터세트를 스캔해서 (0,0)~(1023, 767) 범위를 가진다는 점을 파악하였다. 따라서 데이터세트로 제공되는 이미지는 DSLR로 촬영한 6000×4000 해상도를 가지지만 피실험자들이 실험 중에 보게 되는 화면 위에 프로젝터로 투사되는 영상의 해상도는 1024×768임을 파악할 수 있었다. 따라서 2차원 픽셀 좌표의 범위는 다음과 같다.
| (1) |
프로젝터 영상이 투사되는 실제 화면 위의 직사각형에 가까운 영역이 3차원 공간에서 어떻게 배치되는지 파악하기 위해서 그림 2에서처럼 이 화면을 공간 내 평면으로 근사한다. 화면 왼쪽 상단 모서리의 3차원 공간 좌표를 (x0,y0,z0)이라고 하고 화면의 가로 방향 단위 벡터를 , 세로 방향 단위 벡터를 , 법선 벡터를 이라고 할 때(), 평면 위의 임의의 3차원 점 (xn,yn,zn)는 선형생성(linear span)에 의해 다음과 같이 나타낼 수 있다.
| (2) |
이 때 δx와 δy는 한 픽셀과 인접한 픽셀 사이의 가로 방향 및 세로 방향에서의 물리적 거리로 정의된다. 그런데 δx, δy, 벡터 와 은 한 이미지에서 모두 값이 일정하므로 다음과 같이 새로운 상수 벡터 와 로 식 (2)를 나타낼 수 있다.
| (3) |
식 (3)에서 방정식을 통해서 풀어야 할 미지수는 왼쪽 위에 위치하는 화면의 시작 지점 (x0,y0,z0)와 3차원 벡터 Q, R이다.
| (4) |
미지수가 총 9개이므로 필요한 식의 개수도 최소 9개이어야 한다. 방정식을 풀기 위해 데이터세트에서 제공되는 2차원 이미지 좌표 (a,b)와 이에 대응되는 3차원 좌표 (x,y,z) 쌍을 9개 이상 이용한다. ETH-XGaze 데이터세트에는 충분한 시선 좌표 정보가 제공되기 때문에 9개 이상의 2차원/3차원 데이터 쌍을 확보할 수 있다.
ETH-XGaze 데이터세트에서 i번째, j번째 2차원/3차원 데이터 쌍을 각각 생각하면 식(3)으로부터 다음과 같이 좌측 상단의 화면 시작 지점 (x0,y0,z0)을 소거할 수 있다.
| (5) |
따라서 식 (5)의 결과에서 프로젝터 영상이 실제로 투영되기 시작하는 이미지 좌표의 원점(0, 0)에 대응되는 3차원 위치(x0,y0,z0)를 알지 못하더라도 평면을 구성하는 벡터 Q와 R을 알 수 있고 다음 식으로 와 을 통해 평면의 법선 벡터 n을 구할 수 있다.
| (6) |
| (7) |
추가적으로 ETH-XGaze 데이터세트에서 k번째, l번째 2차원/3차원 데이터 쌍에 대해서도 동일하게 식 (7)과 같은 결과를 얻을 수 있다. x 축에 대해서만 정리하면,
| (8) |
식 (8)은 미지수 Qx와 Rx와 기타 알려진 값들로 구성된 1차 연립방정식이므로 Qx와 Rx로 소거 후 각각 정리하면,
| (9) |
동일한 방식으로 Qy, Qz, Ry, Rz도 구할 수 있다.
| (10) |
| (11) |
식 (9)-(11)에서 와 을 구한 후 가로/세로 방향 픽셀 간 거리 δx와 δy는 와 이 단위 벡터임을 이용해서 다음과 같이 구할 수 있다.
| (12) |
최종적으로 식 (3)에서 프로젝터 화면의 왼쪽 상단 원점 (x0,y0,z0)을 임의의 n 번째 2차원/3차원 한쌍을 통해 다음과 같이 구할 수 있다.
| (13) |
유도한 수식과 실제 데이터를 이용해서 계산한 주요 3차원 공간 데이터는 표 2에서 제시한다. 또한 그림 3에서는 계산된 3차원 정보로 프로젝터 화면과 각 카메라들의 3차원 위치, 카메라 좌표계를 3차원 공간에서 재구성한 그림을 제시한다.
Projector screen (yellow), cameras (red circles) and camera coordinate systems reconstructed with 3D information calculated
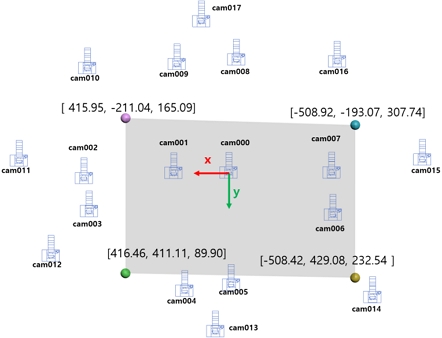
The positions of the 18 cameras and the projector screen positions reconstructed from the calculated 3D information
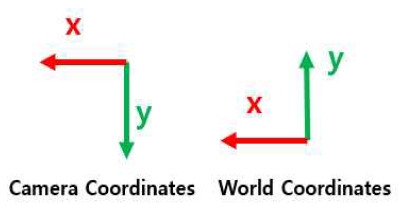
이 데이터세트에서 주의할 점은 18개 카메라의 위치는 y축 방향이 연직 위쪽 방향으로 설정되는 월드 좌표계(그림 5의 오른쪽)에 따라 배치되지만 18개 카메라 각각의 카메라 좌표계의 y축 방향은 연직 아래쪽 방향(그림 5의 왼쪽)으로 설정된다는 점이다. 따라서 기준 카메라(cam000)의 카메라 좌표계의 원점은 월드 좌표계의 원점과 일치하고 두 좌표계의 x축 방향도 일치하지만 y축이 서로 180도 각도를 이룬다.
일반적으로 시선 추적을 위해서는 기준 카메라(예. cam00) 좌표계에서 피실험자의 머리 회전 행렬, 안구의 방향 등 3차원 데이터가 필요하다. ETH-XGaze 데이터세트에서는 이러한 3차원 데이터들 중 일부(머리 회전 행렬, 이동 좌표)만 제공하고 있고 앞서 분석한 프로젝터 화면에서 표시되는 특정점의 좌표와 이 특정점을 바라보는 피실험자의 이미지만 제공한다. 이 정보만으로는 보다 작은 스마트폰이나 태블릿 장치, 웹캠을 설치한 PC 화면 등에서의 시선 추적이나 multi-view 정보 구성 등 다른 응용을 수행하기 어렵다. 따라서 앞서 구성한 프로젝터 화면의 3차원 정보와 함께 피실험자들의 3차원 정보를 재구성할 필요가 있다.
ETH-XGaze의 일차적 목표가 시선 추적이기 때문에 피실험자들의 기하 정보들 중 눈 주변과 안구에 대한 3차원 정보의 파악이 가장 중요하다. ETH-XGaze 데이터세트에서는 18개의 카메라가 동시에 촬영한 이미지를 제공하기 때문에 epipolar gemetry를 이용한 스테레오 카메라 3차원 기하 정보를 다양한 조합으로 추출할 수 있다.
이렇게 epipolar geometry를 이용해서 3차원 정보를 재구성하기 위해서는 이미지 두 장에서 서로 동일한 지점을 파악할 수 있어야 한다. 이러한 목적으로 SIFT[14], SURF[15], ORB 등[16]을 사용하지만 그림 6에서 제시한 것처럼 잘못된 특징점을 대응시키기도 하고 눈 주변 영역과 안구 영역이 아니라 눈 주변의 특정 픽셀들끼리 대응시키는 한계가 있다.
이러한 한계를 극복하기 위해서 epipolar geometry를 이용한 3차원 정보 재구성을 위해 눈 주변의 랜드마크(landmark)를 활용한다. ETH-XGaze에서도 랜드마크 정보를 제공하고 있으나 특히 눈 주변의 랜드마크 위치가 정확하지 않다. 그림 6과 그림 7의 왼쪽 열 이미지 내 빨간색 점으로 표시된 지점들이 ETH-XGaze 데이터세트 내에 포함된 랜드마크 정보들이다. 그러나 그림 7에서 볼 수 있듯이 눈 주변의 랜드마크들이 정확한 위치로 설정되지 않는 문제를 볼 수 있다. 이 문제를 해결하기 위해서 본 논문에서 제안하는 방식에서는 MediaPipe[17]를 이용하며 보다 정확한 랜드마크를 얻는다(그림 7의 오른쪽 열 이미지).
ETH-XGaze 데이터세트에서 제공되는 랜드마크 정보에서는 그림 7의 왼쪽 열에서 볼 수 있는 것처럼 눈 주변에서 오차가 클 뿐만 아니라 눈 주변의 영역만 표시하기 때문에 눈동자가 바라보는 시선 방향의 3차원 벡터를 정확하게 파악하기 어렵다. 본 논문에서 제안하는 방식에서는 이러한 문제를 극복하기 위해서 MediaPipe에서 제공하는 홍채(iris) 추적 기능을 이용해서 눈동자 위치를 파악하였다. 파악된 눈동자(홍채, iris)의 위치는 그림 7에서 마름모 형태로 표시하였다.
그림 7에서처럼 18개의 카메라로 동일 피실험자를 동시에 촬영한 이미지에 MediaPipe를 이용해서 랜드마크를 추출한 다음 일치하는 점들을 기준으로 epipolar geometry를 적용하여 랜드마크에 대한 3차원 위치를 계산한다.
Epipolar geometry 기반 3차원 위치 계산은 [5]에서 제시된 방법을 활용한다. 그러나 [5]에서 다루는 문제와 본 논문에서 다루는 문제가 다른 점은 [5]에서의 문제는 카메라 매개변수가 큰 차이가 있는 RGB 카메라 1대와 IR 카메라 1대를 이용하여 스테레오 이미지를 구성하고 피실험자 모두 마스크를 착용하고 있는 것과는 달리, 본 논문에서는 피실험자가 마스크를 착용하고 있지 않고 카메라 매개변수가 유사한 동일한 규격의 SLR 카메라 18대 중 임의의 2대에서 촬영한 이미지를 이용한다는 점이다. 또한 [5]에서는 눈 주변의 랜드마크들의 평균 위치를 눈의 중심점의 위치로만 파악을 했으나 본 논문에서 제시하는 방법에서는 추가로 그림 7의 오른쪽 이미지에서 제시한 것처럼 홍채의 위치를 정확하게 파악함으로써 3차원 공간에서의 시선 방향 벡터를 보다 정밀하게 파악하였다.
표 3에서는 ETH-XGaze에서 피실험자들의 양쪽 눈의 3차원 좌표를 계산하기 위한 의사 코드를 제시한다.
Pseudo code for parallel processing to compute the 3D positions of the left and right eyes in a RGB image pairs
먼저 epipolar geometry 기반 스테레오 이미지 조합을 구성하기 위해서 18개 카메라들 중 두 개의 카메라에서 촬영된 이미지 시퀀스들을 선택해서 각각 A, B로 정의하고 이 두 이미지 집합을 rbg_eye_pos 함수의 입력값으로 이용한다. 한 쌍의 이미지에서 공통 2차원 랜드마크를 각각 A_point2d, B_point2d라고 할 때 find_3d_position(A_point2d, B_point2d) 함수는 단일 프로세스로서 이 공통 2차원 랜드마크가 3차원 공간에서 위치하는 3차원 좌표를 반환한다. 먼저 선택된 두 카메라의 내부 카메라 매개변수(intrinsic camera parameter)를 이용하여 이미지에서 카메라의 왜곡을 보정(undistort)한다(표 3에서 (A)). 이렇게 보정된 이미지에서 해당 카메라와 이미지 내에 촬영된 공통 랜드마크에 대해 3차원 공간에 위치할 경우 이론적으로 가능한 최소 거리(50mm)와 최대 거리(30,000mm)에 위치할 수 있는 3차원 지점을 각각 계산한다(표 3의 (B)). 그 후 두 이미지에 대해 이론적으로 가능한 최소 거리의 3차원 지점에서 출발해서 최대 거리에 위치한 3차원 지점으로 향하는 광선 ray1과 ray2를 각각의 카메라 매개변수를 이용해서 계산한다(표 3 (C)). 3차원 공간에서 ray1과 ray2가 교차하는 지점이 실제로 해당 랜드마크가 3차원 공간에서 위치하는 지점이며 두 광선이 일치하는 3차원 지점 Q를 계산하여 반환한다(표 3 (D)).
메인 프로세스 eye_pos(A,B)는 논의한 내용을 병렬로 실행함으로써 처리 속도를 향상시킨다. 먼저 MediaPipe를 이용해서 각 이미지 쌍에서 눈과 관련된 랜드마크들을 찾은 후(표 3 (E)) 앞서 설명한 find_3d_position(A_point2d, B_point2d) 함수를 통해 홍채 주변의 랜드마크에 해당하는 3차원 지점들을 찾고 평균을 계산해서 동공의 위치를 계산한 다음 시선 벡터를 계산한다(표 3 (F)).
기하 정보 처리를 위한 수식의 유도 과정과 표 3에 제시한 코드에 대한 보다 자세한 논의는 기존 연구[5]를 참고한다.
2-3 세 대 이상의 카메라를 이용한 3차원 기하 정보 추출
기존 연구[5]에서 논의한 대로 카메라 두 대를 이용해서 epipolar geometry를 기초로 3차원 기하 정보를 추출하는 경우, 3차원 공간의 두 직선의 교점을 계산하는 과정이 필요하다. 세 대 이상의 카메라를 이용할 경우, 카메라 한 대당 고려해야 하는 직선이 하나 씩 추가되며 이 직선들의 교점이 각 카메라로 촬영한 이미지에서 공통되는 2차원 지점에 대한 3차원 위치가 된다. 그러나 일반적으로는 렌즈 매개변수 측정 오차 등으로 인해서 이러한 직선들이 한 점에서 만나는 경우는 거의 없기 때문에 적절한 근사를 적용해야 한다. 본 논문에서는 이러한 근사를 위해 최소제곱법(least squares)의 해를 얻는 normal equation[18]을 적용한다.
3차원 공간에서 직선의 방정식은 두 개의 평면이 만나는 점들의 집합으로 생각하면 행렬식으로 용이하게 표시할 수 있다. 예를 들어 3차원 공간에서 두 점 (ax,ay,az), (bx,by,bz)을 지나는 직선의 방정식은 다음 두 평면이 만나는 점들의 집합으로 생각할 수 있다.
| (14) |
| (15) |
이 방정식을 행렬식으로 표현하면,
| (16) |
| (17) |
위 직선의 방정식은 미지수 x, y, z의 개수(3개)보다 식의 갯수(row 개수, 2개)가 더 적은 전형적인 underdetermined system이다. 다시 말해 직선 위의 여러 점들이 위 방정식을 만족시키는 해가 된다. 일반적으로 epipolar geometry에서는 각 카메라 위치에서 공통 픽셀 위치로 향하는 ray(반직선) 하나 당 위와 같이 식 2개가 구성된다. 따라서 카메라가 추가될 때마다 M과 Z는 “tall matrix”, “tall vector”로 행이 2개씩 증가하게 된다. 이렇게 구성된 선형 방정식 Mx = Z는 카메라가 세 대 이상일 때 overdetermined equation이 되며 최소제곱법(least squares)의 해를 얻는 다음과 같은 normal equation[18]을 이용해서 3차원 공간의 점 x를 계산할 수 있다.
| (18) |
표 4에서는 논의한 방법을 적용한 실제 카메라의 위치 정보와 각도 정보를 정리한다. 카메라 세 대를 사용하며 3차원 정보를 재구성할 이미지 내 공통 지점에 대해 데이터세트에서 제공되는 2차원 좌표는 다음과 같다.
Cam A: [153.0, 204.0]
Cam B: [349.0, 180.0]
Cam C: [0.53, 169.99]
이 때 Cam C에서의 이미지 좌표는 소수점 이하 값이 0이 아닌 실수로 표시되는데 2차원 이미지의 일치 지점을 계산할 때 서브픽셀(subpixel) 단위 값으로 계산되는 것을 볼 수 있다. 이렇게 이미지들 사이의 공통 지점을 계산하는 알고리즘을 통해 얻은 이미지 좌표가 소숫점 이하 값이 0이 아닌 숫자로 계산되는 경우는 해당 이미지의 해상도가 충분하지 않은 상황이라고 해석할 수 있으며 해당 지점의 3차원 좌표 지점을 계산할 때 오차의 또다른 원인으로 작용한다.
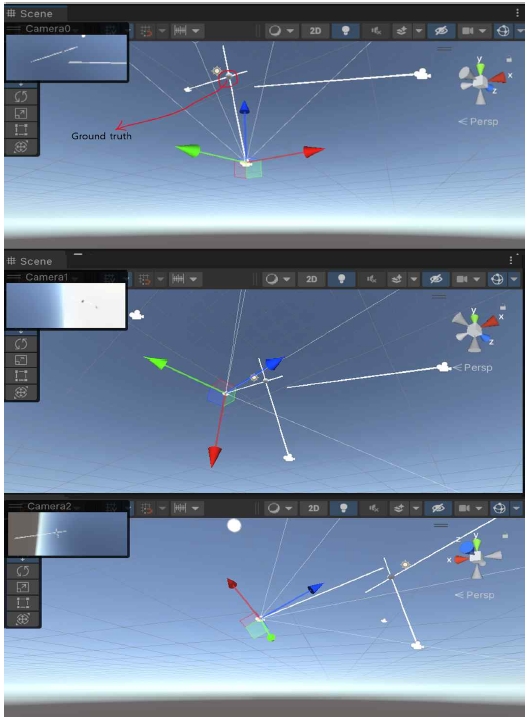
그림 8에서는 이 결과의 이해를 위해 게임 엔진인 Unity3D를 이용해서 각 카메라(이 그림에서는 Cam A, Cam B, Cam C 대신 각각 Camera0, Camera1, Camera2로 표시)의 위치 및 각도와 제안하는 방식으로 계산한 카메라에서의 출발하는 직선(흰색 선)과 최종적으로 계산된 3차원 위치를 표시하고 있다. 이 그림을 보면 2차원 이미지의 공통 위치가 픽셀 단위 좌표로 정확하게 표시되는 Cam A와 Cam B에서 출발한 직선은 한 점에서 정확하게 교차하는 반면, 서브픽셀 단위로 이미지 좌표로 표시되는 Cam C에서 출발한 직선은 나머지 두 직선과 교차하지 않는 것을 볼 수 있다. 앞서 언급한 대로, 이러한 차이는 카메라 매개변수 측정 시 발생하는 오차와 Cam C로 촬영한 이미지의 낮은 해상도 등이 문제가 될 수 있다.
따라서 최소제곱법의 해를 얻는 normal equation을 통해 각 직선에서 가장 가까운 위치의 3차원 정보를 근사적으로 계산한 3차원 좌표는 [127.74, 184.02, 7.60]이다.
Ⅲ. 결 론
인공지능 기술로 인해 컴퓨터 비전 응용 분야가 다양화되고 보다 널리 확산됨에 따라 인공지능 데이터세트를 보다 정확하게 이해할 필요가 대두되고 여러 대의 카메라를 이용한 공간 분석에 대한 요구가 증가하고 있다. 이러한 요구에 따라 본 연구에서는 다중 카메라를 사용해서 측정된 시선 추적용 데이터세트에서 다양한 주변 기하 정보를 재구성하는 방법을 제안한다. 또한 카메라 두 대만을 사용하는 전형적인 epipoloar geometry와 달리 세 대 이상의 카메라를 사용할 때 발생하는 오차 문제와 해결 방안을 제시한다.
본 연구에서 제안하는 방안은 유사한 데이터세트의 활용도를 높이고 다중 카메라에 기반한 다양한 공간 정보 파악 응용 분야에 대한 기본적인 분석으로 활용될 것으로 생각한다.
References
- AI Hub. Eye Movement Video Dataset [Internet]. Available: https://aihub.or.kr/aihubdata/data/view.do?currMenu=115&topMenu=100&aihubDataSe=realm&dataSetSn=548, .
- AIT Lab. ETH-XGaze [Internet]. Available: https://ait.ethz.ch/xgaze, .
-
X. Zhang, S. Park, T. Beeler, D. Bradley, S. Tang, and O. Hilliges, “ETH-XGaze: A Large Scale Dataset for Gaze Estimation under Extreme Head Pose and Gaze Variation,” in Proceedings of the 16th European Conference on Computer Vision (ECCV 2020), Glasgow, UK, pp. 365-381, August 2020.
[https://doi.org/10.1007/978-3-030-58558-7_22]

- Stanford University. CS231A Course Note 3: Epipolar Geometry [Internet]. Available: https://web.stanford.edu/class/cs231a/course_notes/03-epipolar-geometry.pdf, .
-
T. Park, “Obtaining 3D Spatial Information about People Wearing Masks from Stereo Images with Different Color Spaces,” Journal of Digital Contents Society, Vol. 23, No. 12, pp. 2527-2536, December 2022.
[https://doi.org/10.9728/dcs.2022.23.12.2527]

-
T. I. Amosa, P. Sebastian, L. I. Izhar, O. Ibrahim, L. S. Ayinla, A. A. Bahashwan, ... and Y. A. Samaila, “Multi-Camera Multi-Object Tracking: A Review of Current Trends and Future Advances,” Neurocomputing, Vol. 552, 126558, October 2023.
[https://doi.org/10.1016/j.neucom.2023.126558]

-
M. Chandrajit, R. Girisha, and T. Vasudev, “Multiple Objects Tracking in Surveillance Video Using Color and Hu Moments,” Signal & Image Processing: An International Journal, Vol. 7, No. 3 pp. 15-27, June 2016.
[https://doi.org/10.5121/sipij.2016.7302]

-
H. Yang, L. Shao, F. Zheng, L. Wang, and Z. Song, “Recent Advances and Trends in Visual Tracking: A Review,” Neurocomputing, Vol. 74, No. 18, pp. 3823-3831, November 2011.
[https://doi.org/10.1016/j.neucom.2011.07.024]

-
J. Berclaz, F. Fleuret, E. Turetken, and P. Fua, “Multiple Object Tracking Using K-Shortest Paths Optimization,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 33, No. 9, pp. 1806-1819, September 2011.
[https://doi.org/10.1109/TPAMI.2011.21]

-
P. Li, D. Wang, L. Wang, and H. Lu, “Deep Visual Tracking: Review and Experimental Comparison,” Pattern Recognition, Vol. 76, pp. 323-338, April 2018.
[https://doi.org/10.1016/j.patcog.2017.11.007]

-
E. Lindén, J. Sjöstrand, and A. Proutiere, “Learning to Personalize in Appearance-Based Gaze Tracking,” in Proceedings of 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, pp. 1140-1148, October 2019.
[https://doi.org/10.1109/ICCVW.2019.00145]

-
L. Chen, H. Ai, R. Chen, Z. Zhuang, and S. Liu, “Cross-View Tracking for Multi-Human 3D Pose Estimation at Over 100 FPS,” in Proceedings of 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle: WA, pp. 3276-3285, June 2020.
[https://doi.org/10.1109/CVPR42600.2020.00334]

-
M. Zhang, Y. Liu, and F. Lu, “GazeOnce: Real-Time Multi-Person Gaze Estimation,” in Proceedings of 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans: LA, pp. 4187-4196, June 2022.
[https://doi.org/10.1109/CVPR52688.2022.00416]

-
D. G. Lowe, “Object Recognition from Local Scale-Invariant Features,” in Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, pp. 1150-1157, September 1999.
[https://doi.org/10.1109/ICCV.1999.790410]

-
H. Bay, T. Tuytelaars, and L. Van Gool, “SURF: Speeded Up Robust Features,” in Proceedings of the 9th European Conference on Computer Vision (ECCV 2006), Graz, Austria, pp. 404-417, May 2006.
[https://doi.org/10.1007/11744023_32]

-
E. Rublee, V. Rabaud, K. Konolige, and G. Bradski, “ORB: An Efficient Alternative to SIFT or SURF,” in Proceedings of 2011 International Conference on Computer Vision, Barcelona, Spain, pp. 2564-2571, November 2011.
[https://doi.org/10.1109/ICCV.2011.6126544]

- Google. MediaPipe [Internet]. Available: https://google.github.io/mediapipe/, .
- G. Strang, Least Squares Approximations, in Introduction to Linear Algebra, 5th ed. Wellesley, MA: Wellesley-Cambridge Press, ch. 4.3, pp. 219-227, 2016.
저자소개

1997년:서울대 전기공학부 (공학사)
1999년:서울대 전기공학부 대학원 (공학 석사, 반도체 물리 전공)
2006년:서울대 전기컴퓨터공학부 대학원 (공학박사, 컴퓨터 그래픽스 전공)
2006년~2013년: 고려대학교 연구교수
2013년~2017년: 덕성여자대학교 정보미디어대학 디지털미디어학과 조교수
2018년~현 재: 덕성여자대학교 공과대학 사이버보안 부교수
※관심분야:컴퓨터그래픽스, 인공지능, 시선 추적, 수치해석, 3차원 모델링