준지도 이상탐지를 위한 다층 홉필드 신경망
Copyright ⓒ 2023 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
본 논문에서는 준지도 이상탐지를 위한 다층 홉필드 신경망(MHNN)을 제안한다. MHNN은 에너지 기반 모델 중의 하나인 현대 연속 홉필드 네트워크(MCHN)의 구조를 가지며, 에너지 함수가 다층 신경망을 갖도록 확장되었다. 이러한 MHNN의 에너지 함수은 이상탐지를 위한 검출 기준으로 사용된다. 그리고 MHNN의 학습을 위해 contrastive divergence와 score matching을 이용한 경사도 기반 파라메터 갱신법을 각각 제시한다. 제안된 기법을 평가하기 위해 ECG, UNSW 그리고 Fashion MNIST/MNIST를 이용한 준지도 이상탐지 실험을 수행한다. 제안된 MHNN이 단층의 MCHN와 기존의 에너지기반 기법들보다 더 높은 F1-score을 보여준다. 결과적으로 제안된 MHNN이 이상탐지에 있어 매우 효과적인 에너지 기반 모델임을 나타낸다.
Abstract
This study proposes a multi-layer Hopfield neural network (MHNN) for semi-supervised anomaly detection. MHNN comprises the structure of a modern continuous Hopfield network (MCHN), which is an energy-based model, and is extended so that the energy function has a multi-layer neural network. The energy function of MHNN is used as a detection criterion for anomaly detection. We present the gradient-based parameter update methods for MHNN training, using contrastive divergence and score matching. To evaluate the proposed technique, semi-supervised anomaly detection experiments were conducted using ECG, UNSW and Fashion MNIST/MNIST. The proposed MHNN showed a higher F1-score than the single-layer MCHN and conventional energy-based techniques. Consequently, we indicate that the proposed MHNN is a highly effective energy-based model for anomaly detection.
Keywords:
Hopfield Network, Energy-based Model, Multi-layer Neural Network, Anomaly Detection키워드:
홉필드 네트워크, 에너지 기반 모델, 다층 신경망, 이상 탐지Ⅰ. 서 론
이상탐지는 정상적인 패턴과 일치하지 않는 이상 패턴을 식별하기 위한 기법이며 다양한 응용이 가능한 연구 분야이다. 최근에 딥러닝 기술의 발전으로 딥러닝 기반 이상탐지에 대한 연구가 활발하게 진행되고 있으며, 많은 응용 분야에서 기존 방법보다 뛰어난 성능을 나타내고 있다[1]. 딥러닝을 사용한 이상탐지는 주로 사이버 보안 침입 탐지[2], 사기 탐지(fraud detection)[3], 결함 탐지[4], 시스템 상태 모니터링[5], 센서 네트워크의 이벤트 탐지[6], 이미지 결함 검출[7] 그리고 의료 진단[8] 등 다양한 분야에 적용되고 있다.
딥러닝 기반 이상탐지 기법은 정상과 비정상 데이터에 대한 label의 유무에 따라 지도(supervised), 비지도(unsupervised) 그리고 준지도(semi-supervised)로 분류한다[1]. 지도 이상탐지는 데이터의 label을 사용해 binary 또는 multi-class 분류기를 학습해 탐지하는 방법이다. 비지도는 데이터의 label을 없이 학습하고 탐지하는 기법이며, 준지도는 한 클래스(보통 정상) 데이터만을 이용하여 학습한 후 비정상을 탐지하는 기법이다. 이상탐지의 한 가지 중요한 문제는 데이터의 수집이다. 정상 데이터의 수집은 상대적으로 쉽지만 이상 데이터의 획득은 어렵고 데이터의 labeling에 많은 노력이 필요하다. 따라서 뛰어난 성능에도 불구하고 지도기반 이상탐지 보다는 수집이 쉬운 정상 데이터만을 사용하는 준지도기반 기법이 많이 연구되고 있다[1].
준지도 이상탐지를 위한 딥러닝 기법으로는 autoencoders (AEs)[9], generative adversarial networks (GANs)[10] 그리고 에너지 기반 모델(Energy-based Models, EBMs) 등[11]-[13]이 있다. 이들 기법 중에서 EBM을 이용한 이상탐지에 대한 많은 연구가 진행되고 있다. EBM은 에너지 함수를 통해 관측 데이터의 확률 분포를 모델링하기 위해 사용되는 기법이다. 에너지 함수로 다양한 형태의 신경망(Neural Networks, NN)이 사용되기 때문에 비정규화된 분포 형태를 갖고 있지만 여러 가지 데이터를 확률적으로 모델링하는데 매우 뛰어난 성능을 갖고 있다[12]. 대표적인 EBM에는 단층 구조를 갖는 RBM(Restricted Boltzmann Machine)[14]와 HN(Hopfield Networks)[15] 그리고 다층 구조를 갖는 CEBM(Conjugate EBMs)[16]와 EBLVM(Energy-based Latent Variable Model) 등[17]이 있다. 이러한 EBM은 준지도 이상탐지를 위해 정상 데이터만을 이용하여 모델을 학습하고 EBM의 에너지 함수 또는 입력에 대한 재생에러(reconstruction error)를 통해 정상/비정상을 탐지하고 있다.
HN은 EBM중에서 최근 가장 주목 받고 있는 모델이다[15],[18]-[20]. HN는 초창기 인공 신경망의 하나로, 에너지 함수를 통해 가장 가까운 기억 패턴을 검색하는 간단한 연상기억(associative memory) 모델이다[15],[18]. 모델의 패턴 분리 기능, 모델의 수렴 속도 그리고 저장 용량(storage capacity)를 향상시키기 위해 새로운 에너지 함수 도입을 통해 현대 이산 HN(또는, dense associative memory)[19],[20]가 개발되었다. 그리고 최근에는 이산 패턴 대신 연속적인 값을 갖는 패턴과 상태(입력)를 사용하기 위해 현대 연속 HN(Modern Continuous HN, MCHN)[15]가 제안되었다. 이러한 MCHN의 에너지 함수는 상태에 대한 이차항과 log-sum-exp(lse) 함수를 사용해 정의된다. 이 에너지 함수의 중요한 특성은 local minimum로 수렴성, 기하급수적인(exponential) 저장 용량 그리고 일회 업데이트 후 수렴 성질을 갖고 있다. 특히 새로운 에너지 함수의 업데이트 식은 transformer[21]의 self-attention과 같은 형태를 갖는 특징이 있다[15]. 그러나 MCHM의 에너지 함수는 단층 구조의 신경망를 갖는 단점이 있다. 따라서 다층 신경망을 구성하기 위해 이를 계층적으로 구성하거나 신경망의 부분 모듈로만 사용되고 있다.
본 논문에서 이상탐지를 위해 MCHN의 에너지 함수를 새롭게 정의하여 다층 신경망 구조를 갖는 다층 홉필드 신경망(Multi-layer Hopfield Neural Network, MHNN)을 제안한다. 그리고 MHNN의 에너지 함수를 통해 이상탐지를 위한 검출기준을 제시한다. MHNN은 단층 구조를 갖는 MCHN의 에너지 함수를 변형하여 다층 구조를 갖도록 확장한 신경망이다. MHNN은 다층구조를 가진 EBM이기 때문에 입력 데이터의 확률분포를 MCHN보다 더 잘 모델링할 수 있다. 또한 제안된 MHMM을 학습하기 위해 기존 EBM에서 사용된 constrative divergence(CD)[12]와 score matching(SM)[12],[13] 기법을 통해 각각에 대한 MHNN의 목적함수를 유도하고 경사도(gradient)기반 파라메터 갱신법을 제시한다. 제안된 MHNN의 성능 평가를 위해 ECG[22], UNSW[23] 그리고 Fashion MNIST[24]/MNIST[25] 데이터를 사용한 준지도 이상탐지 실험을 진행한다. 실험 결과 제안된 MHNN은 기존의 MCHN, AE, CEBM 그리고 DELVM보다 다층 구조하에서 더 효과적인 F1-score 성능을 나타내었다.
본 논문 Ⅱ장에서는 기존의 EBM과 MCHN을 소개하고, 제안된 MHNN의 구조와 학습 방식을 제시한다. III장에서는 실험 및 결과를 나타내고, Ⅳ에서는 결론을 맺는다.
Ⅱ. 본 론
2-1 EBM과 MCHN 소개
MCHN은 기존 EBM의 하나의 형태이다[15]. 따라서 이 단원에서 기존의 EBM과 MCHN의 구조를 살펴보고, EBM을 학습하기 위한 CD와 SM기법을 간단히 소개한다. EBM은 에너지 함수를 통해 확률분포를 정의하기 위한 확률적인 모델이다[12]. 먼저 입력 데이터 x은 알려지지 않은 실제 데이터 분포 pdata (x)로부터 발생된 확률변수라고 가정한다. EBM의 목적은 에너지 함수에 의해 정의된 모델분포 pθ (x)을 통해 데이터 분포 pdata (x)을 근사화하는 것이다. 입력 x에 대한 EBM의 모델분포 pθ (x)은 다음과 같이 정의된다[12].
| (1) |
여기서 Eθ (x)는 에너지 함수를 나타내며, θ는 모델분포의 파라메터이다. 그리고 Zθ는 정규화 상수, 또는 파티션(partition) 함수라 한다. 이때 에너지 함수의 형태로 다양한 형태의 단층 또는 다층 신경망이 사용되고 있다. EBM의 학습은 식(1)을 이용해 실제 데이터 분포 pdata (x)를 근사하기 위한 모델분포 파라메터 θ을 구하는 것이다. EBM을 학습하기 위한 대표적인 기법은 CD와 SM이 있다[12],[13]. CD 기법은 경사하강법을 통해 pdata (x)와 pθ (x)사이의 Kullback-Leibler divergence(KLD)을 최소화하는 방식으로 θ를 구한다. 그러나 파티션 함수 Zθ 때문에 KLD의 경사도를 정확하게 구할 수 없어 Markov chain monte carlo(MCMC)[26] 기법을 통해 모델분포로부터 샘플링된 추정치를 구하여 근사적으로 경사도를 구하게 된다. 반면 SM 기법은 데이터 분포 pdata (x)와 모델분포 pθ (x)사이의 Fisher divergence(FD)라 불리는 두 분포의 로그 미분값 차이의 유클리드 거리(Euclidean distance)를 최소화하도록 정의된다. 이 기법은 EBM 파티션 함수가 학습에 포함되지 않아 CD 기법보다 학습에 더 효율적인 장점을 갖고 있다[12].
최근에 제안된 MCHN[15]은 식 (1)와 같이 에너지 함수 Eθ (x)에 의해 정의된 EBM 중에 하나로, 입력이 주어진 경우 가장 가까운 기억 패턴을 검색하는 간단한 연상 기억모델 신경망이다. MCHN은 연속적인 값을 갖는 입력 x와 저장된 패턴 W에 대해 다음과 같은 에너지 함수로 정의된다.
| (2) |
여기서 는 상수이고, 행렬 W= (w1,...,wM)는 연속적인 값을 갖는 M개의 저장된 패턴을 나타낸다. 그리고 les(•)은 위의 두 번째 식과 같이 log-sum-exp 함수를 의미한다. 위 MCHN은 RBM[14]과 같은 단층 신경망으로 해석이 가능하다. 입력 x는 입력층을 나타내며, 저장된 패턴 WT는 입력층에서 은닉층으로 연결되는 가중치이다. 따라서 MCHN의 에너지 함수는 입력 x을 가중치 WT에 의해 은닉층으로 변환된 후 les() 함수를 취하는 형태를 갖는다. MCHN은 연산 기억장치로 입력 x에 대해 가장 가까운 패턴을 구할 때, 갱신 규칙(updated rule)은 다음과 같이 주어진다[15].
| (3) |
여기서 는 softmax 함수로 저장 패턴에 대한 가중치 벡터를 나타낸다. 따라서 갱신된 벡터는 입력 벡터와 저장된 패턴들의 유사도를 나타내는 softmax에 의한 가중치 벡터와 저장된 패턴의 선형결합 형태로 주어진다.
위 MCHN은 연속적인 값을 갖는 입력과 패턴들에 대해 transformer[21]의 self-attention 구조를 갖고 입력을 갱신할 수 있고, 높은 저장 용량을 갖는다는 장점을 갖고 있다[15]. 그러나 단층 구조를 갖는 신경망이므로 좀 더 복잡한 패턴을 저장할 수 있는 다층 구조를 갖지 못하는 단점이 있다. 또한 MCHN은 에너지 함수를 통해 EBM의 형태를 갖고 있지만 연상 기억장치 또는 데이터간의 상관관계를 모델링하는 attention구조로 주로 활용되고 있다. 따라서 MCHN을 다층구조로 확장하고, 이를 확률분포을 모델링하는 EBM으로 에너지 함수를 학습하여 이상탐지와 같은 분야에 적용하는 필요성이 요구된다.
2-2 제안한 MHNN의 구조과 학습
이 단원에서 기존 MCHN의 에너지 함수를 변형하여 다층 구조를 갖는 새로운 MHNN와 이에 대한 학습 방식을 제안한다. 본 논문에서 제안한 MHNN의 에너지 함수는 다음과 같다.
| (4) |
여기서 fθ (x)는 입력 x을 받아 비선형 활성화 함수를 갖는 여러 은닉층을 걸쳐 최종적으로 M개의 은닉 노드로 변환하는 파라메터 θ을 갖는 다층 신경망을 나타낸다. 그리고 fθ (x)j는 최종 은닉층의 j번째 출력을 나타낸다. 식 (4)는 MCHN와 같은 에너지 함수를 통해 다층 신경망으로 확장된 형태를 가지므로 MHNN이라 부른다. 만약 MHNN이 활성화 함수가 없는 단층 구조의 신경망, 즉 fθ (x) = WTx이면, MHNN은 MCHN와 같은 형태가 된다. 따라서 MHNN은 MCHN의 일반적인 형태라 할 수 있다.
새로운 MHNN의 파라메터 θ를 학습하기 위해 EBM 학습를 위한 CD와 SM 기법을 사용한다. CD 기법은 KLD의 목적함수, , (또는 음수 로그-유사도 함수라고 함)을 최소화하도록 SGD (stochastic gradient descent) 방법으로 파라메터를 추정한다. 이때 목적함수에 대한 경사도를 구하면 다음과 같다[12].
| (5) |
여기서 E[]는 평균을 나타낸다. 식 (5)의 첫 번째 항은 학습 데이터로부터 쉽게 계산할 수 있지만 두 번째 항은 모델분포에 대한 기댓값을 계산할 수 없기 때문에 MCMC와 같은 근사적인 샘플링 기법을 사용한다. 이때 모델분포 pθ (x)로부터 새로운 샘플을 얻기 위해 명확한 pθ (x)의 형태가 필요하다. 이를 위해 식 (4)의 에너지 함수를 한 점 x0에서 vector Taylor series expansions를 통해 아래와 같이 근사화 한다.
| (6) |
여기서 c는 나머지 항을 포함한 상수이다. 그리고 gθ (x) = lse(β, fθ (x))이며, ∇x gθ (x)은 함수 gθ (x)의 x에 대한 편미분으로, 다음과 같은 softmax 함수에 의해 주어진다.
| (7) |
여기서 는 Jacobian 행렬이며, softmax(βfθ (x))는 다층 신경망의 출력을 softmax 함수를 취하여 얻는 가중치 벡터이다. 이를 바탕으로 모델분포 pθ (x)는 평균 ∇x gθ (x0), 단위행렬의 공분산을 갖는 다변수 Gaussian 분포, pθ (x) ∝ N(∇x gθ (x0), I)로 근사화할 수 있다. 따라서 단순한 Gaussian 분포로부터 추출된 샘플들을 통해 식 (5)의 두 번째 항의 계산이 가능하고, SGD을 통해 MHNN의 파라메터를 추정할 수 있다.
SM은 EBM을 학습하기 위한 또 다른 기법으로 복잡한 파티션 함수를 계산하지 않고 학습할 수 있도록 개발되었다[12],[13]. SM의 목적함수는 앞에서 언급한 것과 같이 데이터 분포 pdata (x)와 모델분포 pθ (x)의 FD로 다음과 같이 정의된다.
| (8) |
여기서 로그-분포의 일차 미분값을 score 함수라 한다. 따라서 SM 기법은 데이터 score와 모델 score 함수가 일치하도록 학습하는 방식이다. 그러나 식 (8)은 데이터 분포 pdata (x) 항 때문에 계산이 쉽지 않다. 하지만 정규적 조건하에서 아래와 같은 식으로 유도할 수 있다[12].
| (9) |
여기서 첫 번째 항은 에너지 함수에 대한 Jacobian 행렬을, 두 번째 항, tr()은 x에 대한 2차 도함수(Hessian)의 trace을 나타낸다. Jacobian 행렬은 식 (7)과 같고 Hessian의 trace도 비슷하게 구할 수 있다. 에너지 함수에 대해 위의 Jacobian과 Hessian에 대한 계산은 딥러닝 소프트웨어의 자동 미분 패키지를 이용하면 임의의 다층 신경망으로 구성된 에너지 함수에 대해 쉽게 계산이 가능하다. 따라서 MHNN의 SM 학습은 위 목적함수을 최소화하도록 SGD을 통해 반복적으로 파라메터를 갱신한다.
위의 MHNN을 이상탐지에 적용하기 위해 먼저 정상적인 데이터만을 사용하여 CD와 SM 기법을 통해 최적의 파라메터 를 추정한다. 그리고 정상/비정상으로 구성된 테스트 데이터를 다층 신경망의 입력으로 하여 출력을 계산한다. 그리고 마지막으로 아래와 같은 에너지 함수와 임계값을 비교하여 이상탐지의 결정 기준으로 이용한다.
| (10) |
여기서 Th는 임계값을 나타낸다.
Ⅲ. 이상탐지 실험 및 결과
본 논문에서는 제안된 MHNN의 이상탐지 성능을 테스트하기 위해 3가지 데이터 셋, ECG[22], UNSW[23] 그리고 Fashion MNIST[24]/MNIST[25]를 이용한 실험을 수행하였다. 각 모델의 이상탐지 성능을 평가하기 위해 F1-score를 비교하였다.
3-1 ECG
ECG5000은 5000개의 심전도 샘플을 포함한 심전도 이상탐지를 위한 데이터 셋이다[22]. 각 심전도는 140개의 데이터로 구성된다. 데이터는 각 하트비트를 추출하고 보간법을 사용하여 각 하트비트의 길이를 동일하게 만드는 두 단계로 전처리되었다. 학습과 테스를 위해 전체 데이터를 3,998와 1,000개로 나누었다. 이때 정상 훈련 데이터는 1639개를 사용하였다. 데이터는 학습하기 전에 [0,1] 사이로 minmax 정규화를 수행하였다. 각 심전도는 이상에 대해 '1'로, 정상에 대해 '0'로 표시되었다. 제안된 모델의 성능을 비교하기 위하여 이상탐지에 가장 많이 사용되는 AE, 단층 구조의 MCHN, 다층 EBM인 CEBM와 EBLVM을 사용하였다. MHNN과 EBLVM은 CD와 SM 기법을 모두 사용하여 훈련하였다. MCHN을 제외한 모든 모델들은 최대 4개의 다층 구조를 사용하였다.
각 모델의 훈련을 위한 배치 사이즈는 100이며, Adam optimizer을 사용하였다. 각 모델의 학습률과 epoch은 최적의 성능이 나오도록 설정되었다. 각 모델에서 은닉층 마다 (256, 512, 1024, 2048)개 유닛을 사용하여 최적의 성능을 내는 노드 수를 선택하여 다층 신경망을 구성하였다. CEBM 은닉층의 뉴런 수는 모두 2048이고, CD 기반 EBLVM와 MHNN은 (1024,256,512,512), (512,1024,256,2048), SM 기반 EBLVM와 MHNN은 (1024,2048,256,1024), (1024,1024,512,256) 구조를 각각 사용하였다. 단층의 MCHN은 1024개를 사용하였다. MCHN와 MHNN에서 β값은 실험적으로 은닉층의 유닛 수의 제곱근으로 설정하였다. 그리고 임계값은 훈련 데이터의 에너지 함수의 히스토그램에 근거하여 에너지 함수 값의 평균을 중심으로 최적의 값을 선택하였다.
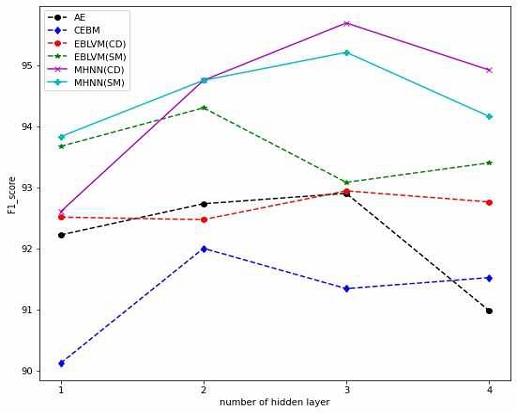
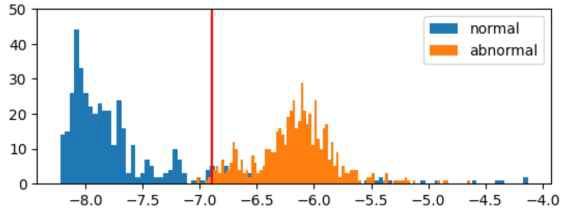
그림 1은 은닉층 수에 따른 각 모델에 대한 F1-score 성능을 나타낸다. SM MHNN와 DELVM은 1개 층일 때 다른 기법에 비해 더 높은 성능을 나타내었다. 한 층을 갖는 MCHN의 성능은 88.3%로 MHNN와 EBLVM에 비해 낮은 성능을 보였다. CD/SM MHNN의 경우 2-3개층에서 성능이 향상되고 4층에서 감소한 반면, EBLVM은 층이 증가할수록 성능이 비슷하거나 저하되는 결과를 나타내었다. CD MHNN은 특히 3개 층일 때 가장 좋은 성능을 나타내었다. 4개 층에서는 성능이 다소 떨어지는데, 이는 층의 수가 증가하면서 파라메터 수도 증가하여 overfitting 문제가 발생하기 때문이다. CEBM은 모든 층에서 MHNN와 EBLVM에 비해 더 낮은 성능을 나타내었다. 제안된 CD/SM MHNN이 다층 구조하에서 다른 EBM 기법과 비교하여 더 향상된 결과를 보여 주었다. 제안된 기법에서 에너지 값에 의한 정상과 비정상 데이터의 분포를 알기 위해 히스토그램을 사용하였다. 그림 2은 정상과 비정상 데이터에 대한 CD MHNN의 에너지값에 대한 히스토그램과 결정에 사용된 임계값을 나타낸다. 이때 정상과 비정상 에너지 값의 평균과 분산은 각각 (-7.7, 0.66)와 (-6.17, 0.35)이며, 최적의 임계값은 –6.89이다.
위의 실험은 같은 EBM 기법에 대해 제안된 MHNN이 ECG 이상탐지 실험에 대해 매우 효과적 있음을 알 수 있다. 그러나 transformer와 같은 최신 기법들을 ECG 이상탐지에 적용한 결과들이 발표되어 높은 성능을 나타내고 있다. 같은 데이터에 대해서 transformer 기반 기법[27]은 99%을 그리고 variational AE[28]는 96.01%의 성능을 보여주고 있다.
3-2 UNSW
UNSW NB15[23]는 네트워크 침입탐지를 위한 대표적인 데이터셋 중에 하나이다. 이 데이터는 실제 네트워크 트래픽을 캡처하여 생성되었으며 정상과 9개의 공격 유형을 가지는 label로 구성되었다. 각 네트워크 데이터는 49개의 특성을 포함한다. 이상탐지를 위해 9개의 공격 유형은 ‘1’로, 정상은 ‘0’으로 표시되었다. 49개의 특성은 연속 값과 이산적인 값을 갖는 네트워크의 특성을 나타내는 값으로 신경망의 입력으로 사용하기 위해 전처리를 통해 최종적으로 188개의 값을 갖도록 하였다. 정상 학습 데이터는 56,000개, 정상/비정상을 포함한 테스트는 82,332개를 사용하였다. 학습을 위한 하이퍼 파라메터는 ECG와 비슷하게 설정되었다.
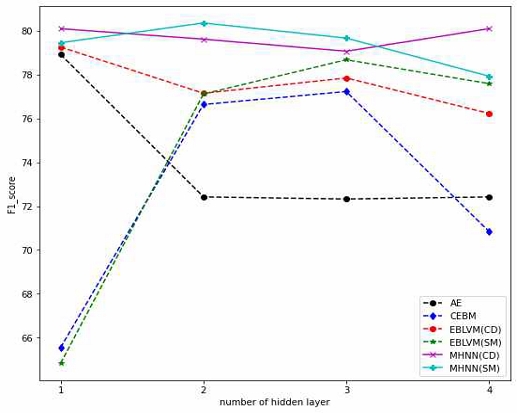
그림 3은 UNSW에서 은닉층 수에 따른 각 모델에 대한 F1-score를 나타낸다. 1개 층일 때 CD/SM 기반 MHNN은 CD EBLVM과 AE와 비슷한 성능을 나타냈고, 다른 기법에 비해 더 좋은 성능을 보였다. 이때 단층의 MCHN은 유닛수가 512일 때 62.6%로 제일 낮은 성능을 보였다. UNSW의 경우 은닉층이 증가할수록 약간의 성능의 증가와 감소가 나타나는 경향을 보이고 있다. 그러나 모든 층에서 제안된 MHNN이 다른 EBM 기법에 비해 더 나은 성능을 유지함을 알 수가 있다. 따라서 UNSW와 같은 네트워크 이상탐지에서도 제안된 기법이 효과적임을 알 수 있다. 그러나 ECG와 마찬가지로 최근의 연구에서는 UNSW를 이용한 이상 탐지 실험에서 83.63%의 F1-score를 나타내어 제안된 기법보다 더 우수한 성능을 나타내었다 [29].
3-3 Fashion MNIST/MNIST
Fashion-MNIST[24]와 MNIST[25]은 28×28 크기와 각각 10개의 클래스를 갖는 gray 이미지를 갖는 데이터 셋이다. 이미지에 대한 이상탐지 실험을 위해 Fashion MNIST를 이상 데이터로 레이블 '1'로, MNIST을 정상적인 데이터로 레이블 '0'를 사용하였다[30]. 정상 테이터로 MNIST 60,000개, 테스트용으로 비정상과 정상으로 Fashion MNIST와 MNIST 각각 10,000개을 사용하였다. 입력 데이터는 784개의 값을 가지며, 전처리 과정으로 표준 정규화 과정을 수행하였다. 학습을 위한 설정은 앞의 두 실험과 비슷하게 구성하였다. 다만 이 실험에서는 (16,32,64,128)개를 사용하여 최적화된 은닉층의 노드 수를 구하였다. 또한 입력값의 차원과 정규화된 값이 크므로 MCHN와 MHNN에서 β값은 마지막 은닉층의 입력수의 제곱근의 역수로 설정하였다.
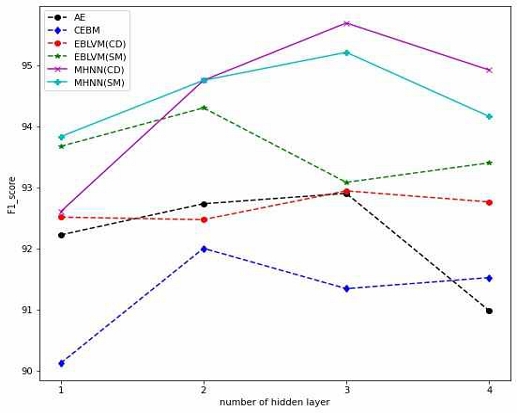
그림 4는 Fashion MNIST/MNIST에 대한 은닉층 수에 따른 F1-score을 나타낸다. 단층의 경우 CD EBLVM이 성능이 가장 높고, 그 다음으로 SM MHNN 그리고 나머지는 비슷한 성능을 나타내었다. 단층의 MCHN은 128개의 노드수에서 88.3%의 결과를 보였다. 2-3층의 경우에 제안된 CD MHNN이 단층에 비해 급격한 성능 향상을 보였으며, CD EBLVM보다 더 좋은 성능을 나타냈다. 4층의 경우 CD MHNN와 EBLVM은 overfitting으로 인해 약간의 성능 하락이 관측되었다. SM 기법들은 CD에 비해 모든 층에서 더 낮은 성능을 나타내었다. 그림 3과 같이 Fashion MNIST/MNIST를 사용한 이미지 이상탐지 실험에서도 제안된 MHNN이 다층 구조하에서 다른 기법들에 비해 매우 효과적임을 알 수 있다.
Ⅳ. 결 론
본 논문에서 단층 신경망 구조의 MCHN의 에너지 함수를 다층 구조를 갖도록 정의하여 새로운 EBM기반의 MHNN을 제안하였다. MHNN의 다층 신경망의 파라메터를 추정하기 위해 CD와 SM 기법을 적용한 목적 함수와 경사도기반의 파라메터 갱신법을 제시하였다. 또한 MHNN의 에너지 함수를 이용하여 이상탐지에 대한 탐지 기준로 사용하였다. 제안된 MHNN을 ECG, UNSW 그리고 Fashion MNIST/MNIST와 같은 다양한 이상탐지를 위한 데이터 셋에 적용하였다. 실험 결과 모든 데이터 셋에 대해서 제안한 MHNN이 단층 구조를 갖는 기존의 MCHN 보다 더 향상된 성능을 나타내었다. 또한 MHNN은 기존 EBM 기법보다 다층 구조에서 더 향상된 F1-score을 나타내었다. 따라서 제안한 MHNN은 에너지 함수를 사용하는 다층 구조의 새로운 EBM 기법으로 이상탐지와 같은 분야에 적용 가능성을 보여 주었다.
그러나 ECG와 UNSW 이상탐지에서 transformer와 같은 최신 기법과 비교해서는 더 낮은 성능을 보여주고 있다. 따라서 앞으로 연구 방향은 제안된 MHNN 기법을 확장하여 transformer와 같이 attention 구조를 더 잘 활용할 수 있도록 연구와 실험을 진행할 예정이다.
References
-
R. Chalapathy and S. Chawla, “Deep Learning for Anomaly Detection: A Survey,” arXiv:1901.03407, , January 2019.
[https://doi.org/10.48550/arXiv.1901.03407]

-
A. L. Buczak and E. Guven, “A Survey of Data Mining and Machine Learning Methods for Cyber Security Intrusion Detection,” IEEE Communications Surveys & Tutorials, Vol. 18, No. 2, pp. 1153-1176, October 2016.
[https://doi.org/10.1109/COMST.2015.2494502]

-
V. N. Dornadula and S. Geetha, “Credit Card Fraud Detection Using Machine Learning Algorithms,” Procedia Computer Science, Vol. 165, pp. 631-641, 2019.
[https://doi.org/10.1016/j.procs.2020.01.057]

-
A. Abid, M. T. Khan, and J. Iqbal, “A Review on Fault Detection and Diagnosis Techniques: Basics and Beyond,” Artificial Intelligence Review, Vol. 54, No. 5, pp. 3639-3664, June 2021.
[https://doi.org/10.1007/s10462-020-09934-2]

-
H. Pandey and S. Prabha, “Smart Health Monitoring System Using IOT and Machine Learning Techniques,” in Proceedings of the 6th International Conference on Bio Signals, Images, and Instrumentation (ICBSII), Chennai, India, pp. 1-4, February 2020.
[https://doi.org/10.1109/ICBSII49132.2020.9167660]

-
V. P. Illiano and E. C. Lupu, “Detecting Malicious Data Injections in Event Detection Wireless Sensor Networks,” IEEE Transactions on Network and Service Management, Vol. 12, No. 3, pp. 496-510, September 2015.
[https://doi.org/10.1109/TNSM.2015.2448656]

-
S. A. Singh and K. A. Desai, “Automated Surface Defect Detection Framework Using Machine Vision and Convolutional Neural Networks,” Journal of Intelligent Manufacturing, Vol. 34, No. 4, pp. 1995-2011, April 2023.
[https://doi.org/10.1007/s10845-021-01878-w]

-
M. Bakator and D. Radosav, “Deep Learning and Medical Diagnosis: A Review of Literature,” Multimodal Technologies and Interaction, Vol. 2, No. 3, 47, August 2018.
[https://doi.org/10.3390/mti2030047]

-
H. Estiri and S. N. Murphy, “Semi-Supervised Encoding for Outlier Detection in Clinical Observation Data,” Computer Methods and Programs in Biomedicine, Vol. 181, 104830, November 2019.
[https://doi.org/10.1016/j.cmpb.2019.01.002]

-
M. Kliger and S. Fleishman, “Novelty Detection with GAN,” arXiv:1802.10560, , February 2018.
[https://doi.org/10.48550/arXiv.1802.10560]

- Y. LeCun, S. Chopra, R. Hadsell, M. Ranzato, and F. J. Huang, A Tutorial on Energy-Based Learning, in Predicting Structured Data, Cambridge, MA: The MIT Press, 2007.
-
Y. Song and D. P. Kingma, “How to Train Your Energy-Based Models,” arXiv:2101.03288, , February 2021.
[https://doi.org/10.48550/arXiv.2101.03288]

- K. Swersky, M. Ranzato, D. Buchman, B. M. Marlin, and N. D. Freitas, “On Autoencoders and Score Matching for Energy Based Models,” in Proceedings of the 28th International Conference on Machine Learning (ICML ’11), Bellevue: WA, pp. 1201-1208, June-July 2011.
- G. E. Hinton, A Practical Guide to Training Restricted Boltzmann Machines, in Neural Networks: Tricks of the Trade, 2nd ed. Berlin, Germany: Springer, ch. 24, pp. 599-619, 2012.
-
H. Ramsauer, B. Schäfl, J. Lehner, P. Seidl, M.Widrich, T. Adler, ... and S. Hochreiter, “Hopfield Networks Is All You Need,” arXiv:2008.02217, , July 2020.
[https://doi.org/10.48550/arXiv.2008.02217]

-
H. Wu, B. Esmaeili, M. Wick, J.-B. Tristan, and J.-W. Van De Meent, “Conjugate Energy-Based Models,” in Proceedings of the 38th International Conference on Machine Learning (ICML 2021), Online, pp. 11228-11239, July 2021.
[https://doi.org/10.48550/arXiv.2106.13798]

-
P. Guo and D. K. Kim, “A New Energy-Based Latent-Variable Model for Unsupervised Feature Learning,” The Journal of Korean Institute of Communications and Information Sciences, Vol. 48, No. 5, pp. 506-516, May 2023.
[https://doi.org/10.7840/kics.2023.48.5.509]

-
J. J. Hopfield, “Neural Networks and Physical Systems with Emergent Collective Computational Abilities,” PNAS, Vol. 79, No. 8, pp. 2554-2558, April 1982.
[https://doi.org/10.1073/pnas.79.8.2554]

-
D. Krotov and J. J. Hopfield, “Dense Associative Memory for Pattern Recognition,” arXiv:1606.01164, , June 2016.
[https://doi.org/10.48550/arXiv.1606.01164]

-
M. Demircigil, J. Heusel, M. Löwe, S. Upgang, and F. Vermet, “On a Model of Associative Memory with Huge Storage Capacity,” Journal of Statistical Physics, Vol. 168, No. 2, pp. 288-299, July 2017.
[https://doi.org/10.1007/s10955-017-1806-y]

-
A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, ... and I. Polosukhin, “Attention is All You Need,” arXiv:1706.03762, , July 2017.
[https://doi.org/10.48550/arXiv.1706.03762]

-
S. K. Berkaya, A. K. Uysal, E. S. Gunal, S. Ergin, S. Gunal, and M. B. Gulmezoglu, “A Survey on ECG Analysis,” Biomedical Signal Processing and Control, Vol. 43, pp. 216-235, May 2018.
[https://doi.org/10.1016/j.bspc.2018.03.003]

-
N. Moustafa and J. Slay, “UNSW-NB15: A Comprehensive Data Set for Network Intrusion Detection Systems (UNSW-NB15 Network Data Set),” in Proceedings of Military Communications and Information Systems Conference (MilCIS), Canberra, Australia, pp. 1-6, November 2015.
[https://doi.org/10.1109/MilCIS.2015.7348942]

-
H. Xiao, K. Rasul, and R. Vollgraf, “Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms,” arXiv:1708.07747, , August 2017.
[https://doi.org/10.48550/arXiv.1708.07747]

- AT & T Labs. MNIST Handwritten Digit Database [Internet]. Available: http://yann.lecun.com/exdb/mnist, .
- D. J. C. MacKay, Information Theory, Inference and Learning Algorithms, Cambridge, UK: Cambridge University Press, 2003.
-
A. Alamr and A. Artoli, “Unsupervised Transformer-Based Anomaly Detection in ECG Signals,” Algorithms, Vol. 16, No. 3, 152, March 2023.
[https://doi.org/10.3390/a16030152]

-
P. Matias, D. Folgado, H. Gamboa, and A. V. Carreiro, “Robust Anomaly Detection in Time Series through Variational Autoencoders and a Local Similarity Score,” in Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021), Online, pp. 91-102, February 2021.
[https://doi.org/10.5220/0010320500002865]

-
O. Aouedi, K. Piamrat, G. Muller, and K. Singh, “Intrusion Detection for Softwarized Networks with Semi-Supervised Federated Learning,” in Proceedings of IEEE International Conference on Communications (ICC 2022), Seoul, pp. 5244-5249, May 2022.
[https://doi.org/10.1109/ICC45855.2022.9839042]

-
S. Vernekar, A. Gaurav, V. Abdelzad, T. Denouden, R. Salay, and K. Czarnecki, “Out-of-Distribution Detection in Classifiers via Generation,” arXiv:1910.04241, , October 2019.
[https://doi.org/10.48550/arXiv.1910.04241]

저자소개

2014년:전남대학교 전자 공학과 학사
2018년:전남대학교 전자 공학과 석사
2021년 3월~현 재: 전남대학교 전자 공학과 박사과정
※관심분야:영상처리, 기계학습, 딥러닝

1989년:전남대학교 전자공학과 학사
1991년:포항공과대학 전자전기공학과 석사
2003년:서울대학교 전기컴퓨터공학부 박사
1991년 2월~1999년 2월: 삼성전자 전문연구원
2003년 4월~2004년 2월: 한국전자통신연구원 선임연구원
2004년 2월~현 재: 전남대학교 전자공학과 교수
※관심분야:딥러닝, 기계학습, 인공지능신호처리