머신러닝 기반 생존분석기법을 활용한 고객 이탈 예측 기술
Copyright ⓒ 2023 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
본 연구에서는 가전 렌탈사업의 적극적인 고객이탈관리를 위한 이탈예측모형을 통하여 어떤 가입자가 이탈할 가능성이 있는지 및 언제쯤 이탈 징후를 보이는지 등을 추정한다. 이를 위해 렌탈 서비스 가입에 대한 고객 계약정보, 인구통계학적 정보, 접점 및 방문 이력 등의 고객-기업 상호작용 데이터를 통합적으로 분석하여 생존분석기법(Survival Analysis) 기반 이탈예측을 모델링하였다. 본 연구에서는 벤치마크 데이터셋이 아닌 실제 운영 데이터셋(정수기 279,259 계정)을 머신러닝기반 Survival Analysis 을 활용하여 고객별 이탈 시기 예측 모델에 적용하였고, 모델의 가장 우수한 성능은 RandomSurvivalForest의 확장 알고리즘인 ExtraSurvivalTrees에서 c-index 기준 약 75%로 평가되었다. 생존 함수 기반 기간별 이탈 확률을 제공함으로써, 리텐션 마케팅 전략에 따라 원하는 타겟 개월 후 이탈 확률 높은 고객 대상을 선정하여 해지 방어 활동을 실행할 수 있도록 지원하고자 한다.
Abstract
In this study, we use a churn prediction model to identify the subscribers who are likely to churn and when they would churn to perform active customer churn management in the home appliance rental business. To this end, demographic information, contract details, and customer-company interaction data such as customer call/visit history, were comprehensively analyzed to develop the survival analysis-based churn prediction model. An actual operational dataset containing 279,259 accounts for water purifiers (not the benchmark dataset) was applied to the model for predicting each customer's churn time using machine learning-based Survival Analysis. The best performance of the model was evaluated to be about 75% based on c-index in ExtraSurvivalTrees, which is an extension of RandomSurvivalForest algorithm. By calculating the probability of churn by period based on the survival function, we aim to select customers with a high probability of churn after the target month according to the retention marketing strategy and support them to execute churn prevention activities.
Keywords:
Digital Technology, Big Data Analysis, Machine Learning, Customer Churn Prediction, Customer Retention Management키워드:
디지털 기술, 빅데이터 분석, 머신러닝, 고객 이탈 예측, 고객 유지 관리Ⅰ. 서 론
고객 이탈 예측 영역에서 고객 이탈은 기업이 일정 기간 동안 고객을 잃는 것을 의미하며, 수익성에 상당한 영향을 미칠 수 있으므로 기업의 주요 관심사이다. 고객 이탈은 제품 또는 서비스에 대한 불만, 더 나은 상품 및 서비스를 제안하는 경쟁업체 또는 고객 개인의 상황 변화와 같은 다양한 이유로 인해 발생할 수 있다. 또한, 고객 이탈을 예측하는 것은 이탈 위험에 처한 고객을 식별하고 이탈이 발생하지 않도록 사전 조치를 취할 수 있기 때문에 비즈니스에 중요하다[1]-[3]. 여기에는 고객을 유지하기 위한 프로모션 또는 개인화된 추천 서비스를 제공하거나 고객을 다시 확보하기 위한 리텐션(Retention) 마케팅 전략이 포함된다[4]-[7]. 이러한 다양한 방법으로 고객 이탈을 예측함으로써 이탈 위험에 처해 있는 고객들 중 회사에 기여 가치가 높은 고객에 대한 노력의 우선 순위를 정하여 기업이 리소스를 보다 효과적으로 활용하는 데 도움이 된다[8].
이탈 예측 연구는 간단한 규칙 기반 및 통계 기법에서 복잡한 기계 학습 모델에 이르기까지 고객 이탈을 예측하는 다양한 접근 방식이 있으며, 고객 이탈 예측에 대한 연구는 지난 수십 년간 다양한 비지니스 도메인에서 이루어졌다 [9]-[19]. 초기 연구에서는 단일 머신 러닝 분류 알고리즘을 사용했으며, 이후 앙상블 기반 예측 알고리즘들이 제안되었다[20]-[22]. 최근에는 예측결과의 원인 추정 기법을 포함한 딥러닝 기반의 고객 이탈 예측 모델들이 제안되었다[16],[23]. 한편, 이탈로 잘못 예측된 사용자가 예측 시점으로부터 정확히 레이블링된 특정 기간 안에 떠나지 않더라도 곧 서비스를 이탈하거나 적어도 서비스 이용 충성도를 잃을 가능성이 있는 이진 분류의 한계를 극복하려는 연구가 이루어졌다. 최근까지 이탈여부를 예측하는 이진 분류방법 외에 생존분석(Survival Analysis) 기법을 활용한 이탈 시기 예측에 관한 연구들이 게임이나 금융 분야를 중심으로 진행되어 왔다. 금융권 연구에서는 그리스 은행 데이터를 이용하여 고객 이탈을 연구하고 위험비례모형과 생존분석법을 이용하여 이탈률 증가의 결정요인을 분석하였다[24],[25]. 게임 분야의 이탈 시기 예측을 위해 Survival Analysis 기법을 적용하는 연구들도 존재한다[26],[27]. 최근에는 상용 게임 로그 데이터를 사용하여 게임 데이터 마이닝에 대한 국제 대회를 개최하고 Survival Analysis기법을 게임 로그 데이터에 적용한 사례들을 소개하는 연구활동도 있다[28].
한편, 최근 코로나19 장기화의 여파로 전 산업에 걸쳐 비대면 고객관리 및 마케팅의 중요성이 높아졌다. 실내에서 보내는 시간이 늘어남에 따라 가전제품 가입 서비스에 대한 관심과 요구가 높아졌다. 이에 다양한 비대면 방문 서비스를 관리하고 고객 특성에 따른 마케팅을 진행하는 것이 중요하다. 이에 따라 고객 이탈 가능성을 예측하는 것이 가전 렌탈 사업의 주요 생존 전략 중 하나가 되었다. 따라서 가전 렌탈 사업에서 데이터 기반 고객 이탈 예측 모델링 연구는 가치 있는 연구 기회이다. 그러나 가전 가입자의 실제 계약 데이터 및 서비스 이용 분석을 통한 전략 수립에 대한 연구는 미흡한 실정이다. 가전 제품 구독자의 특성을 분석하여 이탈 위험 관련 정보를 정량화한 연구는 거의 없다.
따라서 본 연구에서는 가전 렌탈 사업의 적극적인 이탈관리를 위한 이탈예측모형을 개발하였다. 본 연구의 목적은 렌탈케어솔루션 사업에서 어떤 서비스 가입자가 이탈할 가능성이 있는지 및 언제쯤 이탈 징후를 보이는지 등을 바탕으로 어떤 리텐션 전략을 타겟으로 삼을 것인가를 결정하는데 있다. 이를 위해 렌탈 서비스 가입에 대한 고객 계약상세정보, 인구통계학적 정보, 고객-기업간 다양한 상호작용 데이터를 통합 분석하여 Survival Analysis 기법을 적용하여 고객의 이탈 시기 예측 모델링을 진행하였다.
본 연구의 모티브가 된 전자회사의 렌탈 서비스 사업에서는 고객이 계약 해지를 요청해 오면 콜센터 응대직원의 사후적 및 소극적 방어 활동을 통해 해지 방어활동을 해왔다. 따라서 본 연구의 목적은 고객 이탈 가능 시기에 대해 효과적으로 학습하고 예측하여 선제적이며 능동적인 이탈 관리가 가능한 고객 이탈 방어 도구를 제안하는 것이다.
본 논문의 기여 사항은 다음 3가지 측면에 있다.
1) 실제 운영 중인 고객 시스템 기반 현업 마케팅 전략 수립을 위한 예측 모델의 사용 중인 고객 계정 대상 예측 성능 분석을 진행하였다. 본 연구의 기존 연구[29]에서 렌탈 케어 서비스 고객 데이터를 활용하여 이진 분류 이탈 예측모델을 개발하여 그 효용성을 입증하였다. 이후, 현업에서의 활용성을 제고하기 위하여 예측 모델 활용의 마케팅 전략 구체화 작업을 진행하였다. 이를 위하여, 예측 시스템의 대상 고객을 결정하기 위한 예측 모델의 마케팅 활용 시나리오의 탐색을 위하여 운영 중(현재 사용 유지 중)인 계정 대상으로 예측 시나리오별 모델의 예측 성능 및 이탈까지 걸리는 소요 기간(Lead-time)을 도출하고, 예측 결과 기반 타겟팅 고객 대상 조건을 탐색하였다.
2) 둘째, 기존 예측 모델을 활용하여 사용 중 계정 대상의 모델 예측 성능 분석 결과, 재현율 대비 정밀도가 현저히 낮게 도출되었으며, 타겟 시점 즉 몇 개월 이내의 이탈 확률을 예측하느냐에 따라 Lead-time이 다르다는 결과를 얻었다. 따라서, 현재 이진 분류 모델의 문제점을 개선하고 현업 마케팅 전략에 효율적으로 활용되도록 Survival Analysis 기반의 고객별 이탈 시기 예측 모델링을 진행하였다. 본 연구에서는 실제 고객 서비스 사용량과 니즈를 나타내기 위해 벤치마크 데이터셋[28]이 아닌 실제 운영 데이터셋(정수기 렌탈 279,259 계정)을 머신 러닝 기반 Survival Analysis 기반으로 고객별 이탈 시기를 예측하기 위한 모델링을 진행하였다. 이탈 예측 모델의 가장 우수한 성능은 ExtraSurvivalTrees기반 concordance-index 약 75%로 평가되었다.
3) 셋째, 마케팅 담당자가 예측결과 기반 판촉 전략 수립 시 활용성 제고를 위한 utility 함수를 제공한다. 우선, 이탈할 predicted risk score를 구해서 1등~n등까지 정렬하여 이 결과에 따라 상위 m명에게 이탈 방지 캠페인 실행할 수 있다. 또한, survival function 기반 n일 안에 이탈할 확률을 제공함으로써, 원하는 타겟 개월 후 이탈 확률 높은 고객 m명에게 해지 방어 활동 실행할 수 있도록 지원한다.
본 논문의 구성은 다음과 같다. 2장에서는 고객 이탈 이진 분류 예측 모형의 적용 가능성 분석 결과 내용을 설명한다. 3장에서는 모델링을 위한 생존 분석 연구를 소개한다. 4장에서는 모델링 적용 및 실험 결과에 대한 분석을 제시한다. 5장에서는 결론 및 향후 연구로 마무리한다.
Ⅱ. 선행 연구 분석
고객 이탈 예측 모델을 활용하여 해지 방어 마케팅 활동을 지원하기 위해서 예측모델의 적합성에 대한 다음 두 가지 질문에 답하고자 한다.
• 첫째, 실제 사용 중인 고객 계정을 대상으로 예측 모델을 활용할 수 있는 적합한 해지 방어 마케팅 전략은 무엇인가?
• 둘째, 고객의 이탈 확률 외에, 고객 이탈하기까지 시간 T에 대한 예측값을 활용할 수 있는가?
2-1 이탈 컷오프(cut-off) 구간별 예측 모델 정확도 실험
마케팅 시나리오는 예측 모델링의 "문제 정의" 단계에서 이미 반영되기 때문에 모든 마케팅 전략 즉 예측 모델 활용 시나리오에 대하여 잘 동작하는 일반화된 모델은 존재하지 않는다. 본 연구의 토대가 된 기존 연구 결과의 예측 모델은 "마케팅 시나리오"에 대한 가이드가 제시되지 않은 상황에서 개발된 고객 이탈 확률을 추정하는 이진 분류 모델이였다[29].
따라서, 실제 운용중인 고객 시스템에 활용이 가능한 시나리오를 탐색해 보고자 특정 추론 시점에 예측한 모델 결과에 대해서 고객이 6개월 또는 1년 이내 이탈할 확률을 추론하는 실험을 진행하였다. 표1은 실험 가설, 평가 방안 및 예상 가능한 활용 시나리오를 보여준다. 표 2는 현재 운영 중인 계정 대상의 예측 모델의 해지 검출력 실험에 대한 방법 및 대상 데이터에 대한 정보를 보여준다.
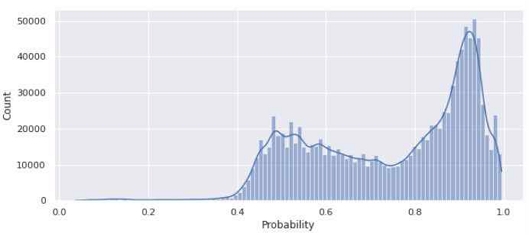
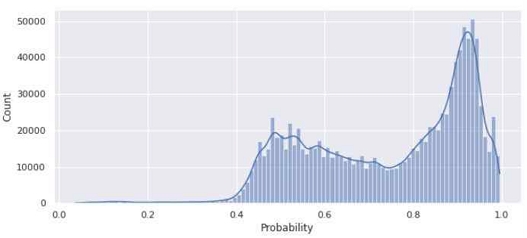
우선, 21년 1월 1일 기준 정수기 서비스 이용 고객 정보 즉 계약시작일로부터 계약종료일 기간 내 21년 1월 1일을 포함하는 고객 계정을 추출하여, 이진 분류 모델을 활용하여 1년 이내의 이탈 확률을 추론하였으며, 그림 1은 예측 모델의 cut-off bin에 따른 고객 계정수 분포를 나타낸다. 그림 2는 그림1의 추론 결과를 사용개월수와 cut-off bin을 기준으로 계정수 비율을 집계한 히트맵(heatmap) 결과이다.
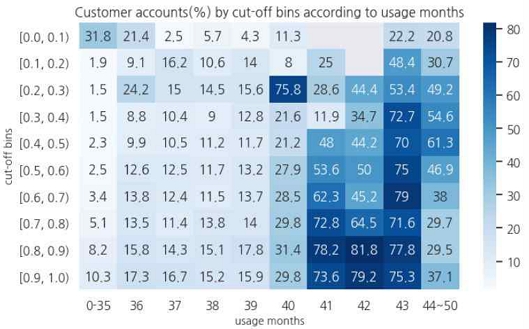
Ratio of the number of customer accounts by cut-off bin according to the number of months of use (probability of churn within 12 months
우선, cut-off 기준으로는 0.5 이하의 구간의 해지계정수 비율은 실제 해지 계정 절대 수가 약 0.1%에 해당하는 구간의 모델의 해지 검출력이 상대적으로 높게 나타난 것이며, 0.5이상의 구간에서는 대체적으로 이탈검출력이 올라가는 경향을 보이며, 사용개월수 기준으로는 41개월에서 43개월사이에서 이탈률이 올라가는 것을 볼 수 있다.
다음으로, 21년 7월 1일 기준 정수기 서비스 이용 고객 정보 즉 계약시작일로부터 계약종료일 기간 내 21년 7월 1일을 포함하는 고객 계정을 추출하여, 이진 분류 모델을 활용하여 6개월 이내 이탈 확률을 추론하였으며, 그림 3은 예측 모델의 cut-off bin에 따른 고객 계정수 분포를 나타낸다.
그림 4는 그림3의 추론 결과를 사용개월수와 cut-off bin을 기준으로 계정수 비율을 집계한 heatmap 결과이다. 우선, cut-off 기준으로는 앞의 실험에서와 유사하게 0.5 이하의 구간의 해지계정수 비율의 크게 튀는 수치들은 실제 해지 고객의 절대 수치가 낮은 경우에 해당하며, 0.5 이상의 구간에서는 대체적으로 이탈검출력이 올라가는 경향을 보였다. 다만, 사용개월수 기준으로는 41개월에서 43개월사이에서 이탈률이 올라갔었던 앞의 실험과는 달리 개월수 간 이탈률 차이의 폭은 거의 나타나지 않았다.
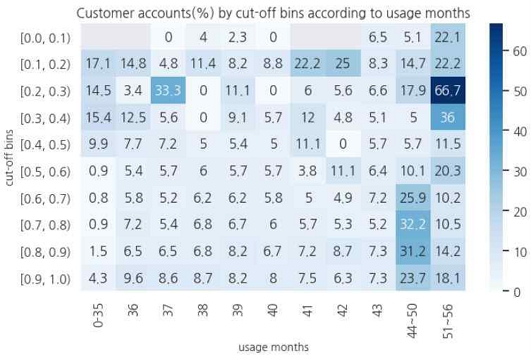
Ratio of the number of customer accounts by cut-off bin according to the number of months of use (probability of churn within 6 months
표 3은 두 가지 실험에 대한 모델의 예측성능을 전체 계정 및 36~43개월 계정에 대하여 보여주고 있다. 예측 정확도에 대한 두 가지 실험 모두 전체 계정 대비 36~43개월 계정에서 예측 성능은 더 나았다. 하지만 90%이상의 높은 재현율에 비해 정밀도는 10% 이내의 매우 낮은 성능을 보였다. 재현율은 좋지만 낮은 정밀도로 인해 f1 성능이 낮은 이유는 학습모델이 계약이 종료된 고객 데이터 셋을 기반으로 이진 분류 라벨링을 진행하여 실제 사용 중(계약 유지 중)인 고객의 feature 분포가 학습모델에 반영되어 있지 않았기 때문이다. 즉, 실제 이탈한 사람들 중 모델이 예측한 사람과의 적중률은 높지만, 예측 모델이 True라고 예측한 사람들 중 실제 이탈자의 수는 작다는 결과를 의미한다. 따라서, 실제 사용 중인 고객 계정 데이터를 기반으로 재학습을 함으로써 정밀도를 보완할 필요성을 도출하였다.
2-2 이탈 cut-off 구간별 이탈 평균 Lead Time 실험
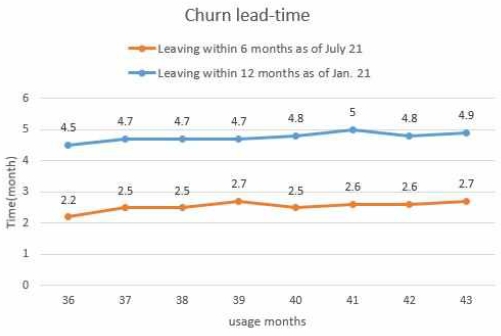
다음으로 cut-off 구간별 실제 해지 Lead-time을 측정하여, 해지방어 액션을 위한 고객 케어링 예상 기간을 추정해보고자 하였다. 실험 방법은 특점 시점에서 모델이 예측한 결과에 대해서 cut-off 구간별, 고객이 해지 진행까지 Lead Time을 도출한다. 고객군 및 cut-off 구간별 모델이 해지를 예상한 고객들의 실제 해지 소요 시간이 상이할 것이라는 가설로 대상 데이터는 2021년 1월 1일 기준, 정수기 서비스 이용 고객 정보와 2021년 12월 31일까지 정수기 서비스 실제 해지까지 소요 기간(일)의 데이터를 활용하였다.
그림 5에서와 같이, Lead-time을 보면 12개월 이내 이탈 확률의 경우와 6개월 이내의 이탈 확률의 경우 Lead-time이 달라지는 결과를 볼 수 있다. 12개월 이내의 경우 약 4.5에서 5개월 정도의 Lead Time이 걸리고, 6개월 이내의 경우 2.2에서 2.7개월의 Lead-time이 걸리는 것을 볼 수 있다. 또한 본 실험에서 다 포함하지 못한 다른 모든 개월 수에 따른 Lead-time은 다를 것이며, 고객별 차이도 존재할 것이다. 따라서, 고객별 이탈 시기에 따른 맞춤형 고객 이탈 방어 캠페인 실행 가능하도록 고객별 이탈 시기를 예측하는 모델링이 추가적으로 필요함을 도출하였다. 따라서 위의 2가지 한계점을 극복하고자, 계약 상태가 사용 중인 고객을 대상으로 survival analysis 기반의 이탈시기 예측 모델링을 진행하였으며 다음 장에서 세부 내용을 설명한다.
Ⅲ. 생존분석 기반 예측 기법
앞서 언급하였듯이, 사용자 이탈을 예측하는 분류기 대신 사용자의 서비스 수명을 예측하는 회귀 모델을 적용하는 것이 더 적합한 연구 방향이다. 그러나, 이 경우 비이탈자가 관측시점 이후에 떠날 때 확인할 수 없는 검열 문제가 있기 때문에 학습 데이터 세트에 대해 기대 수명을 정확하게 레이블링할 수 없는 문제가 있다. 이 문제를 해결하기 위해 생존 분석을 사용한다[29].
3-1 생존분석 (Survival Analysis)
Survival Analysis는 어떤 사건의 발생 확률을 시간이란 변수와 함께 고려하여, 생존 함수를 추정하는 비모수적 방법인 Kaplan-Meier estimation을 기본으로 하는 통계 분석 및 예측 기법이다[30]. Survival Analysis는 관심 이벤트가 시간 t에서 발생하지 않을 확률을 기반으로 하며, 시간 S(t)에 따른 생존 함수는 일반적으로 해당 확률을 나타내는 데 사용된다.
| (1) |
S(t)는 시간 t 이후의 생존 확률이며, T는 모집단에서 가져온 임의의 수명을 의미한다. S(t)는 0과 1사이이고 S(t)는 t의 감소 함수이다.
위험함수(Hazard Function)는 해당 기간이 시작될 때까지 생존한 경우 대상이 작은 시간 간격 내에 관심 있는 이벤트를 경험할 확률로 정의된다. 일정 기간 동안 계산된 순간 비율이며 이 비율은 일정한 것으로 간주된다. 또한 시간 t에서 관심 있는 이벤트를 경험할 위험으로 간주할 수 있다. 시간 t에서 시작하는 간격에서 이벤트를 경험하는 대상의 수를 시간 t에서 생존하는 대상의 수와 간격 폭의 곱으로 나눈 값이다. 연속 확률 변수가 특정 값과 같을 확률은 0이기 때문이다. 이것이 T에서 (T+ΔT)까지의 특정 시간 간격에서 이벤트가 발생할 확률을 고려하는 이유이다. 목표는 이벤트의 위험을 찾는 것이므로 시간 간격 ΔT가 커질수록 위험이 커지는 것을 원하지 않으며, 따라서 이를 조정하기 위해 수식을 ΔT로 나누며 아래 수식(2)에서 보여준다.
| (2) |
극한 ΔT가 0에 접근한다는 것은 우리의 목표가 특정 시점에서 발생하는 이벤트의 위험을 측정하는 것임을 의미한다. 따라서 극한 ΔT가 0에 접근하면 극히 작은 시간이 생성된다. 여기서 위험은 확률은 아니며, 이는 분자에 확률이 있더라도 분모의 ΔT가 1보다 큰 값이 될 수 있기 때문이다.
성능지표 Concordance Index (C-index)는 Survival Analysis에서 가장 많이 사용하는 정확도 지표이다. 대상의 정확한 생존 시간을 평가하지 않고, 대신 여러 대상의 생존 시간(또는 위험)을 상대적으로 비교하며 사망 순서를 잘 예측하는지 판단하는 지표이다.
아래는 한 쌍을 이루는 대상의 생존시간을 비교하는 수식이다. yi은 사건이 발생한 실제 시각이며, 는 모델이 예측한 시각이다.
| (3) |
위 수식 (3)을 기반으로 C-index는 수식 (4)와 같이 계산할 수 있다.
| (4) |
는 평가 대상이 되는 쌍의 개수이며, I는 주어진 조건이 참인 경우를 추출하는 함수이다. 즉 전체 평가 대상의 쌍 집합 중에서 대상 i보다 오래 생존한 대상 j의 생존함수를 더 크게 예측한 쌍의 비율을 계산하며, 이는 0과 1사이의 값으로 계산된다. 여기서 대상은 반드시 사건이 발생해야 한다는 의미의 의 조건은 중도절단된 i에 대해서는 대상 j가 더 오래 생존했다는 확신의 부족으로 비교 대상에서 제외시킴을 의미한다.
3-2 생존 예측 기법
생존 예측(Survival Prediction) 관련 기법은 비모수적(Non-parametric) 방법, 반모수적(Semi-parametric) 방법, 그리고 기계학습(Machine Learning) 기반 방법들이 존재한다[31]-[33].
Kaplan-Meier 추정기는 생존 함수를 추정하는 데 사용되며, 특정 생존 시간 t 동안 생존한 피험자의 비율을 측정한다. 이 함수는 Kaplan-Meier 곡선을 통해 특정 시간 간격(예: 생존)에서 이벤트의 확률을 나타낸다. 샘플 크기가 충분히 큰 경우 곡선은 연구 대상 모집단의 실제 생존 함수에 접근해야 한다.
| (5) |
ni는 시간 t 이전에 위험에 처한 피험자의 수를 나타내며, di는 시간 t에서 관심 있는 이벤트의 수를 나타낸다.
콕스 비례 위험 모델(Cox Proportional Hazards Model)은 Cox에 의해 도입되었으며 한 번에 여러 변수의 영향을 고려하고 이러한 변수에 대한 생존 분포의 관계를 탐색한다. 다중회귀분석과 유사하나 주어진 시간 t에서의 종속변수가 위험함수라는 차이가 있다. 관심 있는 이벤트가 최대 하나 포함되는 매우 작은 시간 간격을 기반으로 하며, 비례 위험 모델에서 가중치를 추정하기 위한 반모수적 접근 방식(semi-parametric approach)이다. 매개변수 추정치는 가중치의 부분 우도(Partial likelihood)를 최대화하여 도출한다. 기울기 하강법(Gradient Descent)은 Cox 모델을 데이터에 맞추는 데 사용되며, 오차가 최소화되도록 가중치를 찾는 것이다. Cox 비례 위험 회귀 모델의 공식은 다음과 같다.
| (6) |
여기서 t는 생존 시간을 나타내며 위험은 시간이 지남에 따라 달라질 수 있다. h(t)는 n개의 공변량 집합에 의해 결정되는 위험 함수이다. b0(t)는 기준선(baseline) 위험 함수이며 다른 모든 공변량이 0일 때 관심 이벤트를 경험할 확률로 정의된다. 는 부분 위험으로써, 기준선 위험만 늘리거나 줄이는 시간 불변 스칼라 인자이다.
Ⅳ. 예측 모델링 및 적용 결과
4-1 모델링 설계
계약 계정이 이탈까지 걸린 기간을 예측(계약 후 얼마 만에 이탈하는지 예측)하는 것을 예측 목표로 하여, 학습 대상 고객을 추출하였다. 라벨링 시점에 계약 상태가 이미 종료되었거나, 현재 계약 유지 중인 고객들을 선정하였다.
이탈시기 예측 모델링을 위한 라벨링 로직은 다음과 같다. 이벤트 True의 경우는 계약 상태가 해지 완료인 계정이며 기간은 해지완료일로부터 계약생성일의 차이이다. 이벤트 False의 경우는 계약 상태가 ‘사용 중’이거나 재계약을 위해 해지완료한 고객 계정이며, 기간 속성은 현재일로부터 계약생성일의 차이이다. 라벨링 결과 고객 모수는 사용 중인 고객 22만명, 이탈 고객 5만명으로 약 82% 대 18%의 비율을 보였다.
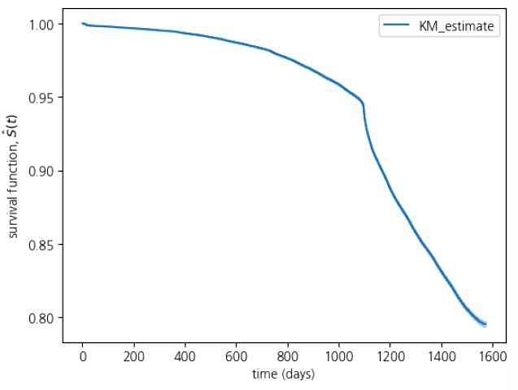
그림 6은 라벨링 데이터 세트의 생존 함수를 추정하는 비모수적 방법인 Kaplan-Meier estimation 추정 개형을 보여준다. 시간이 지날수록 이탈자가 발생하며 생존함수 값이 낮아지는 것을 볼 수 있다. 특히, 1000일을 기점으로 급격히 이탈자가 증가하는 경향을 볼 수 있는데 이는 의무약정기간인 3년이 지난 시점부터인 것을 의미한다.
학습 feature로는 현업의 렌탈 케어 직원의 도메인 지식을 근거로 현재 렌탈 고객의 계약 상세, 접점 이력, 방문 서비스 이력, 할인 이력 등을 활용하였다. 추정 대상으로는 고객 계정이 특정 시간보다 더 오래 생존할 확률인 생존 함수와 특정 시간 T에 사건(이탈)이 발생할 확률 위험함수 기반으로 추정하고자 한다. 성능 측정은 Survival Analysis에서 가장 많이 사용하는 정확도 지표인 C-index를 사용하였다. 대상의 정확한 생존 시간을 평가하지 않고, 대신 여러 대상의 생존 시간(또는 위험)을 상대적으로 비교하는 방식이다. 즉, 이탈 순서를 잘 예측하는지를 판단하는 지표이며, Predicted risk score에 대한 Rank correlation을 의미한다. 완벽한 예측이 1이라면 random guess가 0.5인 것이다. 이탈 예측 결과를 기반으로 이탈 방지 캠페인을 다음과 같이 지원하고자 한다. 우선, 현재 사용 중인 고객 n명을 대상으로 각 고객의 이탈할 predicted risk score를 구해서 1등~n등까지 정렬하고, 상위 m명에게 해지 방어 액션을 실행하는 것이다. 다음으로, 각 고객의 time(개월)별 survival function 기반 이탈 확률 제공함으로써 원하는 타겟 개월(eg. 36개월) 후 이탈 확률 높은 고객 m명에게 해지 방어 활동을 실행할 수 있도록 하는 것이다.
4-2 적용 및 평가 결과
Semi-parametric 기법인 Cox Proportional Hazard model과 machine learning 기반의 방식을 포함하여 예측모델을 평가하였다. Machine learning 기반의 방식은 Fast Survival SVM, RandomSurvivalForest, GradientBoostingSurvivalAnalysis, ExtraSurvivalTrees의 4가지 알고리즘을 비교 실험하였다[34]-[36]. 우선, Cox 모델을 활용하여 타겟변수에 통계적 유의성을 보이는 feature들을 확인하였다. 테이블에서는 전체 feature들 중 상위 10개의 feature들과 p-value를 보여준다.
평가는 10-fold 교차검증으로 예측 모델을 평가했으며 각 모델 성능의 결과는 표 5에서 보여준다. 성능은 일반적인 분류모델에서 결정 경계에 덜 민감하면서 레이블을 구별하기 위해 안정적인 예측을 할 수 있는지 여부를 측정하는 AUC와 비교될 수 있는 생존분석의 상대적 위험정도의 랭킹의 우수성을 검증하는 c-index 값을 계산하였다. c-index의 직관적인 해석은 여러 대상의 생존 시간(또는 위험)을 상대적으로 비교하며 이탈 순서를 잘 예측했는지에 대한 지표를 제공한다는 것이다. 표에서 볼 수 있듯이, Cox Proportional Hazard model이 baseline 모델로 C-index 약 0.5정도의 낮은 성능을 보였다. Machine learning 방식의 경우, 4가지 알고리즘 중에 ExtraSurvivalTrees가 0.75로 가장 우수한 성능을 보였다.
우리는 고객별 시간에 따른 이탈 추정치를 살펴보기 위해, 테스트 데이터로부터 6개의 인스턴스를 샘플링하였다. 가입 후 3개월, 1년이내, 3년이내, 36개월~43개월, 44개월~51개월, 52개월~60개월의 구간에서 각 샘플을 추출하여 Predict survival function과 Hazard function 값을 추출하여 시간에 따른 생존 확률 및 누적 위험도를 그림 7과 그림8에 도식화하였다.
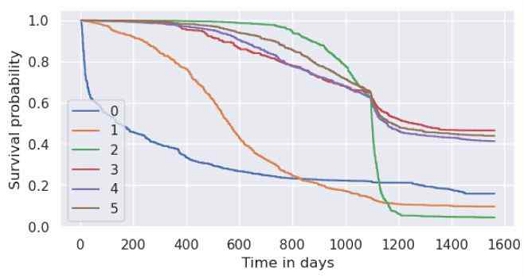
Predictive survival probability according to time in days (six customers sampled from test data, 0: 3 months after contract, 1: within 1 year, 2: within 3 years, 3: 36 to 43 months, 4: 44 to 51 months, 5: 52 to 60 months)
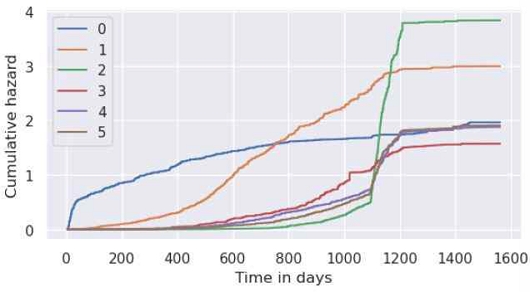
Cumulative hazards according to time in days (six customers sampled from test data, 0: 3 months after contract, 1: within 1 year, 2: within 3 years, 3: 36 to 43 months, 4: 44 to 51 months, 5: 52 to 60 months)
생존 함수(Predict survival function)은 T는 사건 발생 시점이고, t가 관측 중인 임의의 시점일 때 생존 S(t)는 T가 보다 클 확률로써, 시간 t 이후에 인스턴스가 생존할 확률을 의미한다. 예를 들어, 생존 확률이 0.8인 각 인스턴스별 시점은 빠르게는 약 50일전 느리게는 1000일 정도로 어느 시점에 이탈 방지 액션을 취할지에 대한 적합한 선택지를 제공한다. 반대로 위험 함수(Hazard function)는 위험 함수 또는 위험률 h(t)는 개인이 시간 t까지 생존하고 정확히 시간 t에 관심 있는 사건을 경험할 확률을 의미한다. 즉 고객별로 이탈 위험도가 급격이 증가하는 시점을 파악하여 생존함수의 활용방식과 유사하게 이탈 방지 캠페인의 전략에 효과적으로 도입이 가능하다.
utility 함수 첫 번째는 특정 시점 기준으로 그 기간 동안 특정 고객이 이탈하지 않을 확률을 제공하는 함수이다. 두 번째는 누적 위험 함수인데, 특정 시점까지 특정 고객의 누적 이탈 위험수치를 제공한다.
예를 들어, 표 6은 1000일 기준으로 위의 샘플링 테스트 고객 6명의 이탈 위험 확률과 누적 위험 수치를 도출한 예시를 보여준다. 특정 임계치 기준으로 생존 확률 혹은 누적 위험 수치의 고객을 선별하여 타겟 마케팅에 활용이 가능하다.
Ⅴ. 결 론
본 연구에서는 이탈을 예측하는 생존 분석 기반의 통계 및 머신러닝 기법들을 적용하여 그 결과를 분석하였다. 고객 생존과 이탈을 사전에 예측할 수 있다면 서비스에 불만족한 고객이 이탈하기 전에 맞춤형 조치를 취할 수 있을 것이다. 이탈 예측 결과를 기반으로 각 고객의 개월별 survival function 기반 이탈 확률 제공함으로써 원하는 타겟 개월(eg. 가입 후 3개월 이내, 36개월~43개월, 51개월 이후 등) 그룹별로 후 이탈 확률 높은 서로 다른 고객 m명에게 맞춤형 해지 방어 활동캠페인을 실행할 수 있다.
실제 운영 중인 렌탈 서비스 가입에 대한 고객 계약정보, 인구통계학적 정보, 접점 및 방문 이력 등의 고객-기업 상호작용 데이터를 통합적으로 분석한 feature를 사용하고, 가전 기기 렌탈 서비스 구독이라는 도메인 특성이 가지는 계정 계약 특성을 반영한 라벨링 로직을 Survival Analysis 기반 예측 모델링에 적용하여 성능을 검증하였다는 데에 그 학문적 의의가 있다.
본 연구의 한계점으로는 렌탈 서비스 관련 feature 이외의 고객 CRM 데이터, 실제 기기 사용 이력 혹은 외부 데이터와 같은 feature 발굴 작업이 아직 미적용되었다는 점이다. 또한 개발된 예측 모델을 실제 해지 방어 마케팅 캠페인에 적용하여 마케팅 성공률에의 예측 모델의 기여도를 분석하는 작업이 필요하다. 더욱이, 이탈 예측보다 더욱 중요한 것은 실제로 이탈을 방지하고 서비스 품질과 매출을 증대시키는 것이다. 따라서, 이탈 예측의 정확도 기준도 고객에게 제안할 이탈 방지 캠페인의 세부 전략 내용에 따라 달라질 수 있다. 향후, 위험 확률의 임계치 및 생존 기간의 기준치를 마케팅 수익과 비용을 활용하여 최적화하는 연구도 의미 있을 것이다.
References
-
C.-P. Wei and I.-T. Chiu, “Turning Telecommunications Call Details to Churn Prediction: A Data Mining Approach,” Expert Systems with Applications, Vol. 23, No. 2, pp. 103-112, August 2002.
[https://doi.org/10.1016/S0957-4174(02)00030-1]

-
S. A. Qureshi, A. S. Rehman, A. M. Qamar, A. Kamal, and A. Rehman, “Telecommunication Subscribers’ Churn Prediction Model Using Machine Learning,” in Proceedings of 8th International Conference on Digital Information Management (ICDIM 2013), Islamabad, Pakistan, pp. 131-136, September 2013.
[https://doi.org/10.1109/ICDIM.2013.6693977]

-
E. Ascarza, R. Iyengar, and M. Schleicher, “The Perils of Proactive Churn Prevention Using Plan Recommendations: Evidence from a Field Experiment,” Journal of Marketing Research, Vol. 53, No. 1, pp. 46-60, February 2016.
[https://doi.org/10.1509/jmr.13.0483]

- F. F. Reichheld and W. E. Sasser Jr., “Zero Defections: Quality Comes to Services,” Harvard Business Review, Vol. 68, No. 5, pp.105-111, September-October 1990.
- T. O. Jones and W. E. Sasser Jr., “Why Satisfied Customers Defect,” Harvard Business Review, Vol. 73, No. 6, 88, November-December 1995.
-
M. R. Colgate and P. J. Danaher, “Implementing a Customer Relationship Strategy: The Asymmetric Impact of Poor Versus Excellent Execution,” Journal of the Academy of Marketing Science, Vol. 28, No. 3 pp. 375-387, June 2000.
[https://doi.org/10.1177/0092070300283006]

-
S. A. Neslin, S. Gupta, W. Kamakura, J. Lu, and C. H. Mason, “Defection Detection: Measuring and Understanding the Predictive Accuracy of Customer Churn Models,” Journal of Marketing Research, Vol. 43, No. 2, pp. 204-211, May 2006.
[https://doi.org/10.1509/jmkr.43.2.204]

-
M. Zhao, Q. Zeng, M. Chang, Q. Tong, and J. Su, “A Prediction Model of Customer Churn considering Customer Value: An Empirical Research of Telecom Industry in China,” Discrete Dynamics in Nature and Society, Vol. 2021, 7160527, August 2021.
[https://doi.org/10.1155/2021/7160527]

-
I. Ullah, B. Raza, A. K. Malik, M. Imran, S. U. Islam, and S. W. Kim, “A Churn Prediction Model Using Random Forest: Analysis of Machine Learning Techniques for Churn Prediction and Factor Identification in Telecom Sector,” IEEE Access, Vol. 7, pp. 60134-60149, May 2019.
[https://doi.org/10.1109/ACCESS.2019.2914999]

-
P. K. Dalvi, S. K. Khandge, A. Deomore, A. Bankar, and V. A. Kanade, “Analysis of Customer Churn Prediction in Telecom Industry Using Decision Trees and Logistic Regression,” in Proceedings of 2016 Symposium on Colossal Data Analysis and Networking (CDAN), Indore, India, pp. 1-4, March 2016.
[https://doi.org/10.1109/CDAN.2016.7570883]

-
S. Gupta, D. R. Lehmann, and J. A. Stuart, “Valuing Customers,” Journal of Marketing Research, Vol. 41, No. 1, pp. 7-18, February 2004.
[https://doi.org/10.1509/jmkr.41.1.7.25084]

-
B. Zhu, B. Baesens, and S. K. L. M. vanden Broucke, “An Empirical Comparison of Techniques for the Class Imbalance Problem in Churn Prediction,” Information Sciences, Vol. 408, pp. 84-99, October 2017.
[https://doi.org/10.1016/j.ins.2017.04.015]

-
E. Stripling, S. vanden Broucke, K. Antonio, B. Baesens, and M. Snoeck, “Profit Maximizing Logistic Model for Customer Churn Prediction Using Genetic Algorithms,” Swarm and Evolutionary Computation, Vol. 40, pp. 116-130, June 2018.
[https://doi.org/10.1016/j.swevo.2017.10.010]

-
Y. Ahn, D. Kim, and D.-J. Lee, “Customer Attrition Analysis in the Securities Industry: A Large-Scale Field Study in Korea,” International Journal of Bank Marketing, Vol. 38, No. 3, pp. 561-577, October 2019.
[https://doi.org/10.1108/IJBM-04-2019-0151]

-
A. De Caigny, K. Coussement, K. W. De Bock, and S. Lessmann, “Incorporating Textual Information in Customer Churn Prediction Models Based on a Convolutional Neural Network,” International Journal of Forecasting, Vol. 36, No. 4, pp. 1563-1578, October-December 2020.
[https://doi.org/10.1016/j.ijforecast.2019.03.029]

-
B. He, Y. Shi, Q. Wan, and X. Zhao, “Prediction of Customer Attrition of Commercial Banks Based on SVM Model,” Procedia Computer Science, Vol. 31, pp. 423-430, December 2014.
[https://doi.org/10.1016/j.procs.2014.05.286]

-
G. Nie, W. Rowe, L. Zhang, Y. Tian, and Y. Shi, “Credit Card Churn Forecasting by Logistic Regression and Decision Tree,” Expert Systems with Applications, Vol. 38, No. 12, pp. 15273-15285, November-December 2011.
[https://doi.org/10.1016/j.eswa.2011.06.028]

-
K. Na, J. Lee, E. Kim, and H. Lee, “A Securities Company’s Customer Churn Prediction Model and Causal Inference with SHAP Value,” The Korea Journal of BigData, Vol. 5, No. 2, pp. 215-229, December 2020.
[https://doi.org/10.36498/kbigdt.2020.5.2.215]

-
M.-S. Chang and H. J. Kim, “A Customer Segmentation Scheme Base on Big Data in a Bank,” Journal of Digital Contents Society, Vol. 19, No. 1, pp. 85-91, January 2018.
[https://doi.org/10.9728/dcs.2018.19.1.85]

-
Q.-F. Wang, M. Xu, and A. Hussain, “Large-Scale Ensemble Model for Customer Churn Prediction in Search Ads,” Cognitive Computation, Vol. 11, No. 2, pp. 262-270, April 2019.
[https://doi.org/10.1007/s12559-018-9608-3]

-
J. T. Hancock and T. M. Khoshgoftaar, “CatBoost for Big Data: An Interdisciplinary Review,” Journal of Big Data, Vol. 7, 94, November 2020.
[https://doi.org/10.1186/s40537-020-00369-8]

-
C. Tang, N. Luktarhan, and Y. Zhao, “An Efficient Intrusion Detection Method Based on LightGBM and Autoencoder,” Symmetry, Vol. 12, No. 9, 1458, September 2020.
[https://doi.org/10.3390/sym12091458]

-
J. H. Park and H. S. Lee, “A Study on the Prediction Model of Customer Leakage in Financial Companies by Deep Learning: Deducing SME Finance Implications,” Journal of SME Finance, Vol. 40, No. 1, pp. 45-74, March 2020.
[https://doi.org/10.33219/jsmef.2020.40.1.003]

-
N. Glady, B. Baesens, and C. Croux, “Modeling Churn Using Customer Lifetime Value,” European Journal of Operational Research, Vol. 197, No. 1, pp. 402-411, August 2009.
[https://doi.org/10.1016/j.ejor.2008.06.027]

-
M. Mavri and G. Ioannou, “Customer Switching Behaviour in Greek Banking Services Using Survival Analysis,” Manage. Finance, Vol. 34, No. 3, pp. 186-197, February 2008.
[https://doi.org/10.1108/03074350810848063]

-
Á. Periáñez, A. Saas, A. Guitart, and C. Magne, “Churn Prediction in Mobile Social Games: Towards a Complete Assessment Using Survival Ensembles,” in Proceedings of 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Montreal, Canada, pp. 564-573, October 2016.
[https://doi.org/10.1109/DSAA.2016.84]

-
M. Viljanen, A. Airola, T. Pahikkala, and J. Heikkonen, “Modelling User Retention in Mobile Games,” in Proceedings of 2016 IEEE Conference on Computational Intelligence and Games (CIG), Santorini, Greece, pp. 1-8, September 2016.
[https://doi.org/10.1109/CIG.2016.7860393]

-
E. Lee, Y. Jang, D.-M. Yoon, J. Jeon, S. Yang, S.-K. Lee, ... and K.-J. Kim, “Game Data Mining Competition on Churn Prediction and Survival Analysis Using Commercial Game Log Data,” IEEE Transactions on Games, Vol. 11, No. 3, pp. 215-226, September 2019.
[https://doi.org/10.1109/TG.2018.2888863]

-
Y. Suh, “Machine Learning Based Customer Churn Prediction in Home Appliance Rental Business,” Journal of Big Data, Vol. 10, No. 1, 41, April 2023.
[https://doi.org/10.1186/s40537-023-00721-8]

-
J. A. Bogonko, G. Orwa, A. Wanjoya, “Modeling of Average Survival Time for a Loss to be Handled in Insurance Company,” American Journal of Mathematical and Computer Modelling, Vol. 5, No. 1, pp. 18-21, February 2020.
[https://doi.org/10.11648/j.ajmcm.20200501.13]

-
P. Wang, Y. Li, and C. K. Reddy, “Machine Learning for Survival Analysis: A Survey,” ACM Computing Surveys, Vol. 51, No. 6, pp. 1-36, February 2019.
[https://doi.org/10.1145/3214306]

-
J. Tobin, “Estimation of Relationships for Limited Dependent Variables,” Econometrica, Vol. 26, No. 1, pp. 24-36, January 1958.
[https://doi.org/10.2307/1907382]

-
E. Liu and K. Lim, “Using the Weibull Accelerated Failure Time Regression Model to Predict Time to Health Events,” BioRxiv, 362186, August 2018.
[https://doi.org/10.1101/362186]

-
S. Pölsterl, N. Navab, and A. Katouzian, “Fast Training of Support Vector Machines for Survival Analysis,” in Proceedings of European Conference, ECML PKDD 2015: Machine Learning and Knowledge Discovery in Databases, Porto, Portugal, pp. 243-259, September 2015.
[https://doi.org/10.1007/978-3-319-23525-7_15]

-
H. Ishwaran, U. B. Kogalur, E. H. Blackstone, and M. S. Lauer, “Random Survival Forests,” The Annals of Applied Statistics, Vol. 2, No. 3, pp. 841-860, September 2008.
[https://doi.org/10.1214/08-AOAS169]

-
K. V. Rashmi and R. Gilad-Bachrach, “DART: Dropouts Meet Multiple Additive Regression Trees,” in Proceedings of the 18th International Conference on Artificial Intelligence and Statistics, San Diego: CA, pp. 489-497, May 2015.
[https://doi.org/10.48550/arXiv.1505.01866]


1997년~2001년:전남대학교 컴퓨터공학과(학사)
2001년~2003년:광주과학기술원 정보기전공학부(석사)
2004년~2011년:광주과학기술원 정보기전공학부(박사)
2011년~현 재: LG전자 CDO (Chief Digital Officer) 부문 책임연구원
※관심분야:빅데이터 분석, 머신러닝, HCI, Context-awareness 등