건강 검진 스케줄링 알고리즘에 대한 연구
Copyright ⓒ 2020 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
우리는 본 논문에서 효율적인 건강검진 스케줄링 알고리즘을 제안한다. 제안하는 알고리즘은 수검자에게 건강검진 시작 전에 방문할 검사실의 순서(경로)와 전체 건강검진 종료 시간을 미리 알려 줄 수 있는 장점이 있다. 수검자가 검사실로 이동하고 대기하고 검사를 받는 시간들을 순차적으로 모델링함으로써 모든 검진 경로들에 대한 소요시간을 계산하였고 이중 최적의 검진 스케줄을 결정할 수 있었다. 이 방식은 검사실별로 스케줄을 예약하고 대기시간을 정확히 추정할 수 있는 알고리즘을 제시함으로써 가능할 수 있었다.
우리는 제안한 알고리즘과 사람이 안내하는 기존의 건강검진 스케줄링 방식과 비교하는 시뮬레이션을 수행하였고, 결과 분석을 통해 제안한 알고리즘의 장점과 약점을 파악하였다. 제안하는 알고리즘은 2분당 한 명 이하로 수검자가 내원하는 경우 기존 방식보다 우월한 성능을 보였다. 이 알고리즘을 실제 건강검진 현장에 적용하기 위해 필요한 기법들과 고려해야할 사항, 개선할 점 등도 기술하였다.
Abstract
In this paper, we propose an efficient health checkup scheduling algorithm. The proposed algorithm has the advantage of informing the examinee of the order (path) of the exam rooms to be visited and the end time of the entire medical examination before the start of the health checkup. By sequentially modeling the time the examinee moves to the examination room, waits, and undergoes examination, the time required for all examination paths was calculated and the optimal examination schedule could be determined. This method could be possible by scheduling a schedule for each exam room and presenting an algorithm that can accurately estimate the waiting time.
We performed a simulation comparing the proposed algorithm with the conventional health checkup scheduling method guided by humans, and analyzed the results to identify the strengths and weaknesses of the proposed algorithm. The proposed algorithm showed superior performance compared to the existing method, when less than one examinee per 2 minutes visits the hospital. Techniques needed to apply this algorithm to the actual health examination site, items to be considered, and points to be improved are also described.
Keywords:
Brute force, Checkup, Scheduling, Simulation, Waiting time키워드:
건강검진, 대기시간, 스케줄링, 시뮬레이션, 완전탐색Ⅰ. 서 론
건강검진 스케줄링 문제는 건강검진을 위해 병원에 내원하는 모든 사람들(수검자, Examinee)에게 최적의 검진 스케줄을 제시하는 문제를 말한다. 검진 스케줄이란 수검자가 받을 검사들의 조합(Permutation)이다. 예를 들어, 어느 수검자가 1, 2, 5번 검사를 받기 원하는 경우, (1, 2, 5), (1, 5, 2), (2, 1, 5), (2, 5, 1), (5, 1, 2), (5, 2, 1) 등 총 6개의 검진 스케줄(경로, Path)이 존재한다.
최적의 검진 스케줄이란 가능한 검진 스케줄 중 시간이 가장 적게 소요되는 검진 스케줄을 말한다. 건강검진을 위해 소요되는 시간은 검사를 위해 소요되는 시간, 검사실간 이동시간, 다른 수검자들과 검진 스케줄이 겹침으로 인해 발생하는 대기시간으로 구성 된다 .
현재 대부분의 병원에서는 컴퓨터 알고리즘에 의해 건강검진 스케줄링을 하지 않고 있다. 기본적인 검사만 진행하는 규모가 작은 병원에서는 모든 수검자들이 정해진 순서에 따라 동일한 순서(스케줄)로 검사를 받는다. 전문적인 검진 체계를 갖추고 다양한 검진을 하는 병원의 경우, 수검자가 특정 검사를 마치면 검사자가 판단하여 남은 검사들 중 대기시간이 가장 적어 보이는 검사실로 수검자를 안내한다. 이렇듯 현장에서는 사람이 건강검진 안내를 하는 것이 당연시 되고 있어서 건강검진 스케줄링 자동화에 대한 필요성이 크게 인식되고 있지 않다. 이러한 이유로 지금까지 발표된 건강검진 스케줄링에 대한 연구 문헌은 거의 전무하다.
모든 분야가 ICT와 결합하여 자동화 및 지능화하는 4차 산업혁명의 도래와 사람 간 접촉을 최소화하는 언텍트(Untact) 시대의 흐름 속에서, 건강검진 안내를 위한 플로어매니저(Floor manager) 역할을 소프트웨어가 대체함으로써 발생하는 인건비 절감, 효율적인 스케줄링으로 인해 더 많은 수검자를 수용함으로 얻는 병원의 수익 증대 등의 효과를 본 연구를 통해 기대할 수 있다.
건강검진 스케줄링 문제는 그래프에서 두 노드사이에 최소 거리 경로를 찾는 최단 경로(Shortest path) 알고리즘들과는 유사한 듯 보이나 차이가 있다[1],[2]. 건강검진 시 노드인 검사실에 다른 수검자가 먼저 와서 검사를 받거나 기다리는 경우에는 대기 후 방문이 가능하다. 에지의 가중치가 수검자들의 검진 스케줄에 의해 시간에 따라 변하기 때문에 전통적인 그래프 방식을 적용하여 건강검진 스케줄링을 모델링하기는 쉽지 않다.
기존의 병원과 관련된 스케줄링에 대한 연구는, 병원의 제한된 상황과 환자의 건강 상태 등의 복잡한 제한조건 하에서 환자들이 치료나 진단을 목적으로 병원 내의 여러 장소들을 방문하는 최적의 시간을 결정하는 문제들을 다루었다. 하지만, 건강검진은 환자가 아닌 일반인을 대상으로 하며 치료가 아닌 검사를 목적으로 하고 제한된 공간에서 길지 않은 시간 안에 검사실들을 이동한다는 점에서 기존 병원 스케줄링에 관한 연구들과 다소 차이가 있다.
기존 병원 스케줄링 관련 연구를 살펴보면 다음과 같다. 병원의 스케줄링 문제는 상황에 따라 다양한 모델이 고려되는데, 요청에 대한 응답시간에 따라 온라인 스케줄링과 오프라인 스케줄링으로 나눌 수 있다. 온라인 스케줄링은 요청한 스케줄을 즉각적으로 제시하는 알고리즘을 사용하는데 반해[3], [4], 오프라인 스케줄링의 경우 사람, 장비, 장소 등 관계된 여러 자원들의 활용 가능 여부 및 사용 스케줄 등이 연류 되어 매우 복잡한 모델을 사용하는 경우가 많다[5], [6], [7].
상황에 따라 최적 해가 아닌 최적 해에 가까운 휴리스틱(Heuristics)을 제시하는 알고리즘도 있으며[8][9], 온라인 스케줄링의 경우 스케줄링을 위해 탐색 공간(Search space)을 좁히는 경우도 있다[10], [11], [12].
우리는 2장에서 모든 검사실의 시간대 별 대기시간을 정확히 추정할 수 있는 알고리즘을 제시함으로써 검진 스케줄의 소요 시간을 계산하는 방법을 제안한다. 이를 통해 수검자에게 최적의 스케줄을 제시하는 새로운 검진 스케줄링 알고리즘을 제안한다. 3장에서는 시뮬레이션을 통해 사람에 의해 수행해 온 기존 스케줄링 알고리즘과 제안하는 알고리즘을 비교하고 결과를 분석한다. 4장에서는 제안한 알고리즘을 병원 현장에 적용할 때 고려할 사항 및 알고리즘의 약점을 분석하고 보완책을 제언한다. 그리고 5장에서 결론을 맺는다.
Ⅱ. 검진 스케줄링 알고리즘
우리는 건강검진 스케줄링 문제를 건강검진을 위해 내원하는 모든 수검자들에게 최소 시간이 소요되는 검진 스케줄을 제시하는 최적화 문제로 생각한다. 우리는 먼저 도착하여 검진을 받고 있는 기존 수검자들의 검진 스케줄이 존재할 때, 방금 병원에 도착한 새 수검자 한 명을 위한 최적의 스케줄을 제시하는 알고리즘을 제안한다. 하루의 첫 번째 수검자와 같이 먼저 도착해 있는 수검자들이 존재하는 경우는 미리 정해 놓은 방식에 따라 스케줄을 부여한다.
2-1 알고리즘 개요
이 건겅검진 스케줄링 문제의 솔루션은 수검자가 원하는 검사들로 이루어진 모든 경로(Path, 조합)들의 소요시간을 추정하여, 최소 소요시간을 가지는 경로를 찾는 완전 탐색(Brute force) 방식으로 구할 수 있다. 이는 모든 경로를 조사하기 때문에 최적해(Optimal solution)를 보장한다.
병원의 총 검사실 수를 N이라 하고 검사실들을 번호 1, 2, ···, N으로 대응시키자. 이 중 수검자가 받고자 하는 검사 개수를 n이라 하고 수검자가 받고자하는 검사들의 집합을 Q라 할 때, Q ⊆ {1,2,…,N}이다.
이 때, 최적의 검진경로를 찾기 위해 검토해야 할 검진 경로는 집합 Q의 조합(Permutation)들이다. 검진 경로 P1P2…Pn에서 i번째 방문할 검사실의 번호를 Pi라 할 때 Pi ∈Q (i= 1, …,n)이다. 시간의 단위는 편의상 분(分)으로 설정하였고 모든 시간은 분으로 환산한다. 예를 들어, 9시 10분은 9 × 60 + 10 = 550(분)으로 숫자 550에 대응한다.
우리는 다음 최적화 문제의 해를 구함으로써 이 건강검진 문제의 솔루션을 구할 수 있다.
“수검자가 원하는 n개의 검사로 이루어진 모든 경로를 조사하여, 경로의 순서가 유효하고, 다음 식 (1)의 값을 최소로 하는 경로 P1P2…Pn를 구한다”
| (1) |
여기서, sPi,i는 경로 P1P2…Pn에서 i번째로 검사실 Pi에 도착하는 시간, w(Pi,sPi,i)는 시간 sPi,i에 검사실 Pi에 도착할 때 검사를 받기 위해 대기하는 시간(Waiting time), Δ(Pi-1,Pi)는 검사실 Pi-1에서 Pi로 이동하는데 소요되는 시간을 말한다.
의학적인 이유나 병원 사정으로 어떤 특정 검사는 다른 특정 검사보다 먼저 수행되어야 하는 경우가 있다. 예를 들어 내시경 검사는 늘 마지막에 해야 한다는 제약을 둘 수 있다. 특정 검사들의 순서에 제약을 둘 수 있는데, 우리는 이러한 제약을 모두 지킨 경로를 유효하다고 부른다. 우리는 유효한 경로 중 식 (1)을 최소로 하는 경로를 구한다.
경로 P1P2…Pn에서 i번째로 검사실 Pi에 도착하는 시간을 sPi,i라 하고 이 검사를 마치는 시간을 ePi,i라고 할 때 이는 <표 1>과 같이 구할 수 있다. 모든 수검자는 병원 안내데스크에서 검진을 시작하고 안내데스크를 P0로 표기한다. eP0,0는 안내 데스크에서 수검자 등록 시간으로 정의한다. 또, tPi는 검사실 Pi의 평균 진료시간, w(Pi,sPi,i)는 검사실 Pi에 시간 sPi,i에 도착 시 대기시간을 말한다. 대기시간 w의 값을 할당하는 방법은 4)절에 서 다룬다.
수검자는 sPi,i + 1부터 ePi,i까지 검사실 Pi에 머문다. 검사실 Pi에서 검사받는 시간은 [ePi,i - tpi +1 ePi,i]이다. 각 수검자가 병원을 나서는 예상 검진종료시간은 ePn,n이다. <표 1>을 점화식으로 기술하면 다음과 같다.
| (2) |
| (3) |
수검자의 최적 검사경로 P1P2…Pn가 결정되면, 해당 검사실 별로 예상 진료 시간에 예약을 한다. 스케줄을 업데이트하는 것은 예약을 하는 것을 말한다. 스케줄 S를 먼저 업데이트하고 이를 이용하여 대기시간 w를 업데이트 한다.
S(p,t)는 시간 t에 검사실 (번호) p의 검사 예약 유무를 의미한다. 프로그램 시작 시, 모든 값을 0으로 초기화한다. S(p,t)가 0이면 예약된 검사가 없음을 말하고, 0이 아니면 시간 t에 어느 수검자가 검사를 받을 것임을 말한다. 각 검사실 Pi(i = 1,2,…,n)에 대해,
| (4) |
여기서 대입하는 값 1을 각 수검자의 ID로 대신할 수 있다.
대기시간 w(p,t)는 수검자가 검사실 p에 시간 t(분)에 도착했을 때 검사를 받기 위해 기다리는 시간으로 정의한다. 다음 <표 2>의 예제를 통해 스케줄 S와 대기시간 w의 관계를 유추할 수 있다. 이 예들은 검사실 p의 평균검사시간 tp와 스케줄 S가 주어졌을 때 대기시간 w(p,t)를 결정하는 알고리즘에 대한 통찰을 준다.
이를 통해 최적 경로 P1P2…Pn와 예약 스케줄 S가 주어졌을 때 다음 <표 3>과 같이 대기시간 w 업데이트 알고리즘을 도출할 수 있다.
여기서 count_0s는 배열 S(Pi, •)에서 시점 t부터 시작하여 연속된 0의 개수를 구하는 함수이다.
프로그램 구현시 w와 S는 배열로 선언되는데 모두 0으로 초기화한다. 배열의 크기를 설정하기 위해 접수 마감시간과 병원 종료시간을 설정한다. 다음 <표 4>는 제안한 건강검진 알고리즘의 의사코드를 보여준다.
2-2 제약 조건 수용 방법
검사의 의학적 특성상 또는 병원에서 검사의 효율을 제고하기 위해 지켜져야 하는 규칙이 있는 경우가 있다. 검토 대상이 되는 경로가 이 규칙에 맞는지 여부를 판단하는 것을 유효성 테스트(validity test)라 한다.
예를 들어, 건강검진에서 의학적 특성상 내시경 전 초음파 검사를 받고, 초음파 전 채혈을 하는 경우가 많다. 또한 많은 병원에서 검진의 원활한 진행을 위해 내시경 검사를 마지막에 하는 것을 선호한다. 검사실들이 두 개 층에 나누어 있는 병원의 경우, 수검자들이 1층의 검사를 모두 마치고 2층으로 이동하는 것을 선호하기도 한다. 유효성 테스트는 검사할 항목과 병원의 특성에 따라 달라진다.
우리가 말하는 유효성 테스트는 수검자에게 제시할 경로가 이렇게 필요한 제약 사항들을 모두 지키는 유효한 경로인지 체크하는 것을 말한다. 유효성 테스트는 경로 완전 탐색 시 불필요한 계산을 피하기 위해 경로 소요 시간 식 (1)을 계산하기 전에 수행한다.
유효성 테스트의 구현은 두 가지 방법이 가능하다. 경로(조합)를 모두 생성하여 메모리에 저장해 두고 각각의 경로가 유효한지 체크하여 유효하지 않은 경로를 제거하는 방법과, 경로를 생성하는 함수 안에서 유효하지 않은 조합을 생성 못하게 억제하여 유효한 경로만 반환(return)하도록 하는 방법이 있다. 후자가 메모리 절약, 속도 등의 이점이 있을 수 있다. 하지만, 모든 조합들을 계산하는 것은 기존 함수나 알고리즘을 가져다 써야 하는 경우에 해당하기 때문에, 개발자가 조합들을 계산하는 다양한 방법에 대한 조사와 알고리즘 중간에 개입하여 수정 가능한지 여부의 판단을 잘해야 한다.
지금까지 설명한 알고리즘의 가장 큰 약점은 모든 경로를 조사하기 때문에 시간이 다소 오래 걸릴 수 있다는 점이다. 모든 경로는 수학적으로 조합(permutation)을 의미한다. 예를 들어 15개의 진료실을 방문해야 하는 경우 15!개의 경로를 모두 조사해야 한다. 만약, 검사실을 두 개의 그룹으로 분할해서, 첫 번째 그룹에 속하는 검사를 모두 받은 후에 두 번째 그룹에 속하는 검사를 받게 하는 것이 가능하다면 계산량이 크게 줄어 들 수 있다.
예를 들어, 15개 검사의 가능한 경로의 총 개수는 1,307,674,368,000개이다. 하지만 앞의 8개 검사를 먼저 수행하고 7개 검사를 그 다음에 수행하는 것으로 경로를 제한하는 경우, 처음 8!=40320개의 경로를 조사해서 검사 최소 시간 경로를 구하고, 그 다음 7!=5040개의 경로를 조사해서 검사 최소 시간 경로를 구하여 이어 붙이면 되기 때문에 8!+7!= 45,360으로 고려해야 할 경로의 개수가 현저히 줄어든다. <표 5>는 15개 검사를 두 그룹으로 분할할 때 계산량의 감소를 보여준다. 세 그룹으로 분할할 경우 계산량을 더욱 줄일 수 있다.
검사실 분할은 검사소들의 위치 근접성, 기초 검사를 선행하는 관행 등으로 인해 대부분의 건강검진 병원에서 현실적으로 적용 가능하다. 분할을 적용할 경우, 분할을 유효성 테스트 중 하나로 취급할 수 있다.
각 검사실 별로 하나 이상의 베드(bed)가 있는 경우가 있다. 이 경우 한 검사실에서 하나 이상의 검사가 동시에 진행 가능하다. 이를 구현하기 위해, 우리는 검사실의 각 베드에 스케줄 S와 대기시간 w를 1차원 배열로 할당하고, 위 알고리즘에서 베드 수를 고려한 인덱스 확장이 필요하다.
Ⅲ. 시뮬레이션
우리는 제안한 알고리즘의 성능을 검증하기 위해 제안한 알고리즘과 기존 건강검진 안내 방법과의 비교 시뮬레이션을 수행하였다. 기존 방법은 검사를 마친 검사실의 검사자(examiner)이 남은 검사들 중 대기시간이 가장 적은 검사실로 다음 검사를 정해 주는 방법을 말한다. 현재 거의 모든 건강검진 병원에서는 이와 같은 방법을 사용하나, 또는 미리 정해 놓은 순서에 따라 모든 수검자들이 동일한 순서로 검사를 받게 하고 있다. 우리는 이 시뮬레이션을 통해, 기존 방법과의 성능비교, 효과성, 제안한 알고리즘의 약점 파악, 제안 알고리즘의 정확성 입증 등을 수행하였다.
3-1 시뮬레이션 개요
먼저 검사실은 두 개의 그룹을 이루고 있다고 가정하였다. 절반이 한 그룹이고 나머지가 다른 한 그룹으로서, 그룹 내의 검사실간 이동시간은 1분, 다른 그룹에 속하는 검사실로 이동시간은 2분, 안내데스크에서 모든 검사실로 이동시간은 2분이 걸린다고 가정하였다. 우리는 모든 시간은 숫자로 표시하고 단위는 분(minute)이라 가정한다.
건강 검진을 위한 등록 시작시간은 9시, 이를 숫자로 환산하면 9 × 60 = 540이 된다. 검사등록 마감시간은 15시, 즉 15×60 = 900이다. 구현 시 스케줄과 대기시간 배열의 크기를 정해주기 위해 최대 23시59분까지 검사를 할 수 있다고 가정했다.
검사실의 평균 검사시간은 1 또는 2 또는 3 또는 4로 설정하였고 1이 될 확률은 20%, 2는 40%, 3은 20%, 4는 20%로 설정하였다. 또 검사실의 베드(bed) 수는 1개 또는 2개로 1개일 확률은 50%, 2개일 확률은 50%로 설정하였다.
검사소는 번호로 1부터 시작하여 정수로 표시하였는데 내시경 검사소는 가장 큰 번호로 정하고 내시경 소요시간은 20, 내시경 검사실 내 베드 수는 6개라 가정하였다. 수검자는 안내데스크를 통해 병원에 입장한다고 가정하고 안내데스크의 번호는 0으로 정하였다.
성능에 크게 영향을 미치는 주요 변수에는 검진자수와 검사실수 등 두 가지가 있다. 수검자 수는 100명, 120명, 150명, 180명, 200명 등 5가지 경우, 검사실 수는 10개, 12개, 14개, 16개 등 4가지 경우에 대하여 시뮬레이션을 실시하였다.
오전 9시부터 오후 3시까지 6시간 동안 수검자들이 등록할 수 있기 때문에 6×60 = 360 단위 시간 동안 수검자들이 올 수 있다. 수검자 수는 양적인 의미와 복잡도의 의미를 동시에 가진다. 예를 들어 수검자가 180명이 온다는 이야기는 2분당 한 명꼴로 수검자가 병원에 도착하고 그 만큼 복잡하다는 말이다.
참고로, 경험이 많은 개발자의 말에 의하면 수검자가 수가 하루 평균 300명에 달하는 대형 병원도 있지만, 80명 정도 오는 작은 병원이 많으며, 검사실 수는 12개에서 16개 사이가 실제에 가깝다고 한다.
검사실, 수검자, 유효성 테스트 관련 시뮬레이션 환경 설정을 위해 실무자와 협의하여 다음과 같이 현실성 있게 설정하였다.
검사실별 평균 검사시간은 1분(20%), 2분(40%), 3분(20%), 4분(20%) 중 하나로 랜덤하게 설정하였고, 베드 수도 1개(50%) 또는 2개(50%)중 랜덤하게 선택하였다. 내시경 검사실의 평균검사시간은 20분, 베드 개수는 6개로 고정하였다.
수검자들의 병원 도착시간은 9시와 15시 사이 즉 540과 900사이의 자연수 중 수검자 수만큼 랜덤하게 선택하는 방식으로 설정하였다. 그리고 각 수검자가 받을 검사의 수 n는 검사실수의 40%이상 80%이하로 설정하였다. 예를 들어, 검사실 개수가 16인 경우, 각 수검자는 6.4(=16×0.4)개 이상 12.8(=16×0.8)개 이하 즉 7, 8, 9, 10, 11, 12 중 하나를 랜덤하게 선택하여 선택된 수만큼 검사를 받는다. 검사받을 항목, 즉 방문해야 할 검사실들은 랜덤하게 n개를 선택하였다.
우리는 유효한 경로에 대해 다음과 같이 세 가지 제약 조건을 두었다. 첫 번째는 선행검사 조건으로, 검사 1과 2는 검사 3보다 반드시 앞에 받아야 한다. 두 번째는 분할 조건으로, 검사 1번부터 절반까지가 첫 번째 그룹, 그 다음부터 내시경 검사까지가 두 번째 그룹으로 설정하여 첫 번째 그룹에 속하는 검사가 다 끝나야 두 번째 그룹에 속한 그룹의 검사들을 받을 수 있게 하였다. 세 번째는 내시경 검사를 받는 경우 반드시 마지막에 받아야 한다는 조건을 넣었다.
기존 수동 스케줄링 알고리즘은 한 검사가 종료되는 시점에서, 수검자의 남은 검사들 중 대기시간이 가장 적은 검사를 다음에 받을 검사로 선택한다. 이 규칙은 수검자가 남은 검사 중 다음 식 (5)를 최소로 하는 검사실로 이동하는 탐욕적 알고리즘(greedy algorithm)이라 할 수 있다.
| (5) |
여러 수검자가 차례로 병원에 도착하여 이러한 규칙에 의해 검사를 진행하는 상황에서 각 수검자의 검사 종료시간을 알아내어 제안한 알고리즘과 검사 종료시간을 비교하기 위해 다음 <표 6>과 같이 기존 알고리즘을 구현하였다.
시뮬레이션에서 각 수검자는 MOVE, WAIT, EXAM 중 하나의 상태(state) 값을 취하도록 하였다. 즉 검사받으러 온 수검자는 어느 검사실로 이동하거나(MOVE), 어느 검사실에서 검사받기 위해 기다리거나(WAIT), 검사를 받는다(EXAM). 각 상태마다 일정한 시간이 필요하다. 이를 위해 timer 변수에 값을 할당하였다. 예를 들어, 검사를 받기 시작하면 상태를 EXAM으로 바꾸고 timer에 그 검사실에 평균 검사시간을 할당한다. 또는 이동을 시작하면 상태를 MOVE로 바꾸고 timer에 평균 이동시간을 할당한다.
MOVE가 종료되고 원하는 검사실에 도착했을 때 그 검사실의 모든 베드가 차있으면 상태를 WAIT로 바꾸고 그 검사실의 대기자 명단(Waiting List)에 추가시키고 WAIT 때는 timer 값을 설정하지 않았다.
Patients_in_Hospital은 현재 병원에 있는 사람들의 리스트(배열)을 말하고 TEND는 검사 등록마감시간이다. 매 루프에서 시간 t는 1분씩 증가하도록 하였다.
update_timer() 함수는 모든 진료실의 모든 베드의 대기시간을 1 감소하고, Patients_in_Hospital에 속한 모든 수검자들의 timer를 1 감소시킨다.
update_room_info() 함수에서는 각 검사실의 대기자 명단에 누군가 있으면 비어있는 그 검사실에 베드가 있는지 조사하고 있으면 대기자 명단의 맨 앞에 있는 수검자를 그 베드에 할당하고 수검자의 상태와 timer를 적절히 설정한다. 모든 베드가 검사 중이면 아무 일도 안 한다.
update_patient_info() 함수에서는 Patients_in_Hospital에 속한 모든 수검자들을 조사하여 timer가 0이 된 경우, 위에서 언급한 데로 상태를 바꾸어 주고 timer를 다시 설정한다. 예를 들어, timer가 0이고 현재 상태가 EXAM인 경우는 검사를 마친 것으로 남은 검사가 없으면 병원을 나가게 하고, 남은 검사가 있으면 위에서 언급한 간단한 규칙에 의해 다음 행선지를 정한다. 그리고 상태를 MOVE로 바꾸고 timer를 해당 이동시간으로 설정한다.
add_new_patient(t) 함수는 현재 시간 t에 도착한 환자를 Patients_in_Hospital에 추가한다.
3-2 시뮬레이션 결과
위와 같은 환경에서, 모든 수검자는 기존 알고리즘과 제안한 알고리즘에 의해 검사를 받는다. 그리고 두 방법에 의한 퇴원시간을 비교한다. 비교 기준값 Val은 다음과 같이 정의한다.
| (6) |
Val이 양수이면 기존 알고리즘에 의한 퇴원시간이 더 큰 것으로 기존 알고리즘에 따른 검사 진행이 더 늦었다는 것을 말한다. 우리는 실험에서 각 수검자별로 Val값을 측정하는데, 어떤 수검자의 Val이 양수라면 이 수검자는 제안한 알고리즘으로 검사를 진행했을 때 더 빨리 검사를 마칠 수 있었다고 말할 수 있다.
우리는 랜덤에 의한 극단적인 치우침이나 우연을 최소화하기 위해 100번 반복실험을 하였다. 수검자 수 100, 120, 150, 180, 200과 검사실 수10, 12, 14, 16의 모든 조합에 대해, 반복실험에서 얻어진 100개 수치들의 평균과 표준편차를 이용하여 다음과 같이 세 가지 결과를 분석하였다.
수혜자는 제안한 알고리즘으로 더 빨리 검사를 마친 수검자로서 Val 값이 양수인 수검자이다. 우리는 전체 수검자중 수혜자들의 비율을 구했다. 이 비율이 높을 수 록 많은 수검자들이 제안한 알고리즘으로 인해 혜택을 보고 검사를 빨리 마칠 수 있었다고 말할 수 있다. 즉 이 비율이 높으면 제안한 알고리즘의 우수성을 입증할 수 있다.
이론적으로 보아 제안한 알고리즘이 기존 알고리즘보다 우월하여 100%가 나와야 하는데 <표 7>에서 보듯 실험 결과는 그렇지 않다. 이는 제안한 알고리즘은 처음에 전체 검사실 방문 스케줄을 결정하는데 반해, 기존 알고리즘은 한 검사를 마친 후 다음 검사 항목을 결정하기 때문이다. 이에 관한 설명은 다음 장에서 예시를 들어 설명하겠다.
이는 모든 수검자들의 Val 값 평균을 구하는 것으로, 수검자 한 명당 단축한 검사시간의 평균을 의미한다. 위 수혜자 수와 달리, Val > 0인 경우와 Val ≤ 0인 경우를 모두 포함한다. Val <0인 경우는 단축시간이 음수인 경우로, 제안한 알고리즘이 시간을 더 소비했음을 의미한다.
이를 통해 기존 알고리즘과 비교하여 제안한 알고리즘으로 단축한 평균 시간을 알 수 있다. <표 8>은 수검자 수와 검사실 수 각각에 대해 100회 반복 실험한 결과를 보여 준다.
괄호 안 숫자는 100회 반복에서 얻어진 단축시간 평균의 표준편차를 말한다. 표에서 볼 수 있듯이 수검자 수가 증가할수록 표준편차가 크게 증가하는 것을 볼 수 있다. 이는 수검자 수가 증가할수록 평균에 대해 신뢰도가 떨어진다는 의미이다. 퍼센티지(%) 값은 기존 알고리즘에 의한 검사 소요시간 평균 대비 단축시간의 비율을 말한다. 예를 들어, 수검자가 100명이고 검사실이 10개인 경우, 수검자 한 명당 14.9분이 단축되었으며, 이 단축시간 14.9분은 기존 검사시간의 32.06%에 해당한다.
그리고 환자 수가 200명일 때는 제안한 알고리즘이 기존 알고리즘보다 좋지 못 한 결과를 얻었다. 4장의 4-2에서 이에 관한 이유를 설명한다.
수혜자는 제안한 알고리즘으로 더 빨리 검사를 마친 수검자로 Val 값이 양수인 경우이다. 우리는 <표 8>의 시뮬레이션 결과를 바탕으로 제안한 알고리즘이 기존 알고리즘 보다 우수한지 통계적으로 검증(statistical test)해 보았다. 이 때 사용한 검증 방식은 짝지어진 표본의 비교(paired t-test)로 H0 : δ = 0 vs H1 : δ ≠ 0( 또는 H1 : δ < 0)으로 p-value는 0.01로 설정하였다.
<표 9>는 통계적 검증의 결과를 보여 준다. 표에서 Sig.는 통계적으로 유의미한 것으로, 간단히 말하면, 제안한 알고리즘이 기존 알고리즘보다 더 좋다는 것을 의미한다. Sig.(-)는 기존 알고리즘이 통계적으로 더 좋다는 것을, Insig.는 두 알고리즘의 성능이 통계적으로 우열을 가리기 어렵다는 것을 의미한다.
<표 9>의 시뮬레이션 결과를 통해, 수검자 수가 180이하 인 경우 제안한 알고리즘이 더 우수하며, 수검자수가 200인 경우 둘 간의 차이가 없거나 제안한 알고리즘보다 기존 알고리즘이 더 우수한 것을 알 수 있다. 간단히 말해, 우리 알고리즘은 수검자 수가 180이하인 경우, 즉 2분에 한 명이하의 수검자가 내방하는 복잡도를 가지는 경우에 유효하다고 말할 수 있다.
Ⅳ. 제안 알고리즘 고찰
4-1 파라미터 추정
제안한 알고리즘은 검사실들의 평균진료시간과 검사실들간 평균이동시간이 어느 정도 정확히 설정되었을 때 잘 작동한다. 따라서 이 두 파라미터를 정확하게 추정하는 것이 매우 중요하다.
파라미터 값은 어느 정도 주기를 가지고 업데이트 해 주는 것을 권장한다. 예를 들어, 하루치 데이터들을 얻은 후 평균을 구해서 다음 날 파라미터 값으로 사용할 수 있다. 또는 하루 내 일정시간 간격(예: 2시간 간격)으로 해당 파라미터 측정값들을 평균하여 파라미터 값들을 업데이트 시켜 줄 수 있다.
개인에 따른 오차 발생을 최소화하기 위해, 연령별, 장애유무 등에 따라 파라미터 값들을 유연하게 적용할 수 있다. 예를 들어, 검사실간 이동시간의 경우 수검자의 건강상태에 따라 다음의 k값을 적당히 조절하여 할당할 수 있다.
| (7) |
여기서 Δ(i,j)는 검사실 i에서 검사실 j로의 평균 이동시간이다. 안내데스크에서 판단하여 장애인의 경우 k = 2, 70세 이상 고령자의 경우 k = 1.5로 설정하여 신체능력에 따라 검사실간 이동시간을 길게 할 수 있다.
파라미터들을 실시간으로 추정하여 업데이트하는 방법도 있다. 이는 업데이트 시점을 정해 놓고 그 시간에 파라미터 값을 업데이트를 시키는 것이 아니라 파라미터 측정치가 입력될 때 마다 바로 업데이트한다. 최근 정보가 반영되는 장점도 있지만 이상치에 민감할 수 있는 단점도 있다.
일반적으로 데이터 x1, x2, …, xn,…이 끊임없이 입력될 때, n번째 데이터 xn이 주어졌을 때, 이 데이터들의 평균 m은 다음과 같다.
| (8) |
예를 들어, 검사실 i의 실 검사시간 데이터가 계속 입력될 때, 30번째 입력 데이터까지의 평균값(평균검사시간)은 이다. 여기서 m은 29번째 데이터까지의 평균값이고, 이 값은 30개 데이터들의 평균값으로, 이를 다시 m으로 놓는다. 다른 모든 파라미터들도 이와 같은 방법으로 파라미터 값을 실시간 업데이트 할 수 있다.
또는, 최근 데이터에 더 의존하면서 이상치에 민감하지 않기 위해 다음과 같이 일정한 비율로 이동평균(moving average)을 통해 평균값을 추정할 수도 있다.
| (9) |
여기서 η는 모든 n에 대하여 0.8, 0.85, 0.9, 0.95 중 하나를 선택한다.
4-2 기존 알고리즘이 더 우월한 사례 고찰
이론적으로는 제안한 알고리즘이 기존 알고리즘보다 우월해 보이지만 <표 7>에서 보듯이 시뮬레이션에서는 모든 경우에 대해 100% 우월하다는 결과가 나오지 않았다. 수검자가 200인 경우는 50%~60% 정도만 더 나은 결과가 나왔다.
이는 제안한 알고리즘은 검진 시작 전 전체 검사 스케줄을 결정하는데 반해, 기존 알고리즘은 한 검사를 마친 후 다음 검사 항목을 결정하는 탐욕적인 방식을 택하기 때문이다. 이 경우 한 사람의 비상식적인 선택이 다른 사람에게는 좋은 결과를 초래하는 경우가 발생할 수 있다.
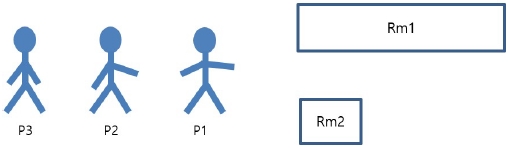
<그림1>의 예시를 살펴보자. Rm1, Rm2의 두 개의 검사실만 있는 병원에 P1, P2, P3 세 사람이 건강검진을 받기 위해 1분 간격으로 순서대로 도착했다고 하자. Rm1, Rm2의 평균검사시간은 각각 10분, 1분이고 베드 수는 한 개일 때, 가장 먼저 도착한 수검자 P1이 검사실 Rm1을 먼저 방문하면, P1은 10분간 검진을 받고 Rm2로 이동할 것이다.
이때, 다음 수검자 P2 입장에서 Rm2가 비어있으니 먼저 Rm2에서 검사를 받고 Rm1로 이동하면 Rm1에서 8분을 대기한 후 검사를 받을 수 있다. 이러한 이유로 P2는 총 검사시간이 19(=1+8+10)분 소요될 것이라 생각하고 Rm2를 먼저 갈 수 있다.
하지만, 다음 수검자 P3가 Rm2로 가지 않고 Rm1을 먼저 간다면, P2는 Rm2에서 검사를 마친 후 P1과 P3가 Rm1에서 검사를 마치기를 기다렸다가 검사를 받아야 한다. 이 경우 P2의 총 소요 시간은 계획과는 다르게 1+8+10+10 = 29분 걸리게 되고, 반면 P3의 소요시간은 7+10+1 = 18분이 되어 P2보다 먼저 검진을 마치게 된다.
이렇듯, 여러 사람의 스케줄이 얽히기 때문에 현명하지 못 한 근시안적 탐욕적인 결정이 더 나은 결과를 낳는 사례가 발생할 수 있다. 우리는 시뮬레이션의 로그 파일을 검토하는 과정에서 이와 같은 사례가 발생하는 것을 확인할 수 있었다.
4-3 환자수 증가에 따른 성능 저하 문제 및 제언
시뮬레이션을 통해 수검자 수가 적을수록 그리고 검사실 수가 많을수록 제안한 알고리즘이 더 효과적인 것으로 드러났다. 수검자 수가 180을 초과하는 경우는 제안한 알고리즘이 효과적이라고 말하기 어렵다.
우리는 수검자 수가 200이고 검사실이 10개인 경우에 대해 100회 반복 실험을 하면서 수검자의 병원 도착순서가 알고리즘의 성능과 관련이 있음을 알게 되었다. 이 경우는 <표 8>에서 보듯이 제안한 알고리즘을 사용할 경우 기존 방식보다 수검자 1인당 평균 8.9분 늦게 검사를 마쳤다.
<그림2>의 x축은 수검자들의 일련 번호로 번호가 낮을수록 먼저 병원에 빨리 도착했음을 의미한다. 막대그래프의 높이는 100번의 반복 실험 중 제안한 알고리즘으로 더 일찍 검진을 마친 수검자의 수이다. 막대의 최대 높이는 100이며 높을수록 제안한 알고리즘이 좋다고 할 수 있다.
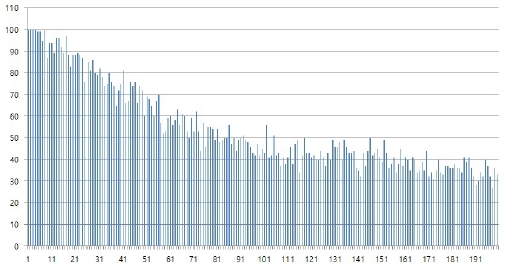
Relationship between the order of arrival to the hospital and the performance of the proposed algorithm.
그래프의 x축 왼편의 병원에 일찍 온 수검자들의 경우 대부분 제안한 알고리즘으로 검사를 일찍 마칠 수 있었지만, x축 오른편의 병원에 늦게 온 수검자들은 제안한 알고리즘으로 좋지 않은 결과를 얻었다. 알고리즘 성능과 병원 도착시간(진료 시작시간)과의 상관관계가 있음을 알 수 있다. 대략 20번째 수검자까지는 90%이상, 40번째 수검자까지는 75%이상 제안한 알고리즘이 효과가 있음을 알 수 있다. 다시 말해, 제안한 알고리즘이 처음에는 높은 성능을 보이다가 시간이 지남에 따라 성능이 저하되는 것을 볼 수 있다.
이 관찰로부터 전체 수검자의 검진 스케줄을 적당한 시간 간격으로 모두 업데이트할 경우 성능 저하를 막을 것이라 기대할 수 있다. 업데이트 시 초기에는 높은 성능을 기대할 수 있기 때문이다. 하지만 시간이 지남에 따라 성능이 저하될 수 있으므로 지속적으로 일정한 시간 간격으로 다시 전체 스케줄을 업데이트할 필요가 있어 보인다.
제안한 알고리즘을 이러한 전략으로 운영할 것을 제안하며, 주기적 업데이트 방식과 효과에 관한 연구는 향후 과제로 남긴다.
Ⅴ. 결론 및 논의
우리는 본 논문에서 건강검진 스케줄링 자동화를 위한 알고리즘을 제안하였다. 기존 건강검진은 모든 수검자가 기존에 정해진 순서대로 검사를 받거나, 검사를 마친 검사실의 검사자가 다음 검사실을 정하여 제시하는 형태로 안내를 하는 방식으로 진행된다.
내원하는 수검자가 많지 않은 병원은 큰 문제가 없으나 수검자가 많고 검사실의 개수가 많은 병원은 조용한 환경에서 혼선 없는 검사 진행을 위해 검진 스케줄의 자동 부여가 요구되었다. 우리는 이러한 이유로 연구를 착수하여 수검자에게 초기에 모든 검진 스케줄을 제시하는 알고리즘을 도출하고 이론적인 측면과 실험적인 측면에서 고찰하였다.
병원 실무자를 통한 사전 조사에서, 검진 초기에 검진스케줄을 모두 제시하는 방식(strategy)은 수검자에게 큰 신뢰를 줄 수 있기 때문에 병원 측에서는 선호하였으며, 2-2에서 언급한 검사실 분할은 실제로 대부분의 병원에서 적용 가능한 방식이었다.
제안한 알고리즘은 완전 탐색(Brute force) 방식으로 조사해야 하는 경로가 많기 때문에 계산량이 많아 보이지만 식(1)의 계산이 배열에서 정수 값을 읽어 와서 더하는 것뿐이기 때문에 시간이 많이 소요되지 않는다. 수검자 한 명당 체감 소요시간은 매우 짧다.
<표 8>에서 현실과 가장 유사한 100명 수검자, 12개 검사실의 경우 제안한 알고리즘은 기존 방식 대비 검사시간을 약 33% 단축할 수 있을 것으로 기대된다. 제안한 알고리즘은 간단하며 효율적으로 적용 가능하다. 하지만 건강검진 현장에 적용하기 위해서는 파라미터를 정확하게 추정하고 업데이트하는 것이 중요하다.
제안한 알고리즘의 가장 큰 약점은 <그림2>에서 보듯이 방문자 수가 많은 경우 후 순위로 도착하는 방문자들의 검사 시간이 점점 오래 걸린다는 것이다. 이는 방문자 수가 많아지거나 검사 종료시간이 길어질 때 모든 수검자들의 스케줄을 업데이트하여 해결할 수 있을 것으로 보인다. 건강검진 스케줄 업데이트는 향후 연구 과제로 남긴다.
Acknowledgments
본 연구는 강남대학교 2019년도 교내 연구비 지원에 의해 수행되었음.
References
-
E. W. Dijkstra “A note on two problems in connection with graphs”, Numerische Mathematik, Vol. 1, pp. 269-271, 1959.
[https://doi.org/10.1007/BF01386390]

- S. J. Russell, Artificial intelligence : a modern approach, 4th ed. Norvig, Peter. Boston:Pearson, 2018.
-
F.-S. Hsieh, “A hybrid and scalable multi-agent approach for patient scheduling based on Petri net models”, Applied Intelligence, Vol. 47, No. 4, pp. 1068-1086, 2017.
[https://doi.org/10.1007/s10489-017-0935-y]

-
P. Kazemian M. Y. Sir, M. O. Van Oyen, J. K. Lovely, D. W. Larson, and K. S. Pasupathy “Coordinating clinic and surgery appointments to meet access service levels for elective surgery”, Journal of Biomedical Informatics, Vol. 66, No.1, pp.105-115, 2017.
[https://doi.org/10.1016/j.jbi.2016.11.007]

-
R. L. Burdett and E. Kozan, “An integrated approach for scheduling health care activities in hospital”, European Journal of Operational Research, Vol. 264, No. 2, pp. 756-773, 2018.
[https://doi.org/10.1016/j.ejor.2017.06.051]

-
A. G. Leeftink, I. M. Vliegen, and E. W. Hans, “Stochastic integer programming for multi-disciplinary outpatient clinic planning”, Health Care Management Science, Vol. 22, No. 1, pp. 53-67, 2019.
[https://doi.org/10.1007/s10729-017-9422-6]

-
M. Rezaeiahari and M. T. Khasawneh, “An optimization model for scheduling patients in destination medical centers”, Operations Research for Health Care, Vol. 15, No.1, pp. 68-81, 2017.
[https://doi.org/10.1016/j.orhc.2017.09.004]

- E. G. M. Kananga, “Agent based patient scheduling using heuristic algorithm”, International Journal on Computer Science and Engineering, Vol. 2, No.01S, pp.69-75, 2010.
-
G. Billiau, C. F. Chang, A. Ghose, A. A. Miller, “Using distributed agents for patient scheduling,” Lecture Notes in Computer Science, Vol. 7057, pp. 551–560, 2010.
[https://doi.org/10.1007/978-3-642-25920-3_40]

-
A. Azadeh, M. Baghersad, M. H. Farahani, M. Zarrin, “Semi-online patient scheduling in pathology laboratories,” Artificial Intelligence in Medicine, Vol. 64, No. 3, pp. 217–226, 2015.
[https://doi.org/10.1016/j.artmed.2015.05.001]

-
A. Braaksma, N. Kortbeek, G. F. Post, F. Nollet, “Integral multidisciplinary rehabilitation treatment planning,” Operations Research for Health Care, Vol. 3, No. 3, pp. 1–18, 2014.
[https://doi.org/10.1016/j.orhc.2014.02.001]

-
E. Castro, S. Petrovic, “Combined mathematical programming and heuristics for a radiotherapy pretreatment scheduling problem,” Journal of Scheduling, Vol. 15, No. 3, pp. 333–346, 2012.
[https://doi.org/10.1007/s10951-011-0239-8]

저자소개

1998년 : 연세대학교 대학원 (이학석사 수학)
2001년 : Texas A&M University 대학원 (이학석사 통계학)
2006년: 연세대학교 대학원 (공학박사 컴퓨터과학)
2007년∼2008년: 강남대학교 컴퓨터미디어공학부, 전임강사
2009년∼2012년: 강남대학교 컴퓨터미디어공학부, 조교수
2013년∼2017년: 강남대학교 컴퓨터미디어공학부, 부교수
2018년∼현 재: 강남대학교 소프트웨어응용학부, 교수
※관심분야: 최적화 알고리즘, 복지기술, 얼굴인식, 기계학습, 딥러닝, 컴퓨터비전, 영상처리 등