컴퓨터 게임에서 소속도를 이용한 NPC의 지능 제어
Copyright ⓒ 2020 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
컴퓨터의 발전으로 컴퓨터 게임은 빠르게 성장하고 있다. 게임에서 자율적 게임 캐릭터는 사용자에게 흥미를 일으키는 중요한 요소이다. 자율적 게임 캐릭터는 컴퓨터가 행동을 제어한다. 일반적으로 자율적 게임 캐릭터는 FSM(finite-state-machine) 방식을 사용한다. FSM 방식은 게임 캐릭터의 제어구조가 간단하다는 장점이 있다. FSM 방식은 게임 디자이너가 자율 게임 캐릭터의 행동을 정의한다. 규칙화된 자율적 게임 캐릭터의 행동 정의는 자율적 게임 캐릭터의 행동에 부자연스러움을 발생시킨다. 본 논문에서는 자율적 게임 캐릭터의 지능적 제어 방식을 제안한다. 본 논문에서 제안한 자율적 게임 캐릭터의 지능적 제어 방식으로 인해서 자율적 게임 캐릭터의 행동에 자연스러움을 발생시키며, 지능적 제어 방식은 게임 상황을 분석하여 자율적 게임 캐릭터의 행동 규칙을 자동 생성할 수 있음을 본 논문에서 분석하였다.
Abstract
The development of computer system and the game industry are accelerating. The Non-Player-Character(NPC)s are the important element that arouse the user’s interest. The actions of the NPCs are controlled by a computer. The NPC generally adopts FSM(Finite State Machine). The FSM has an advantage in terms of a simple structure to control a game character. Moreover, a game designer defines the actions of the NPC in FSM. Regularized behavior definition of NPCs makes behaviors of NPCs unnatural. This paper proposes the intelligent control approach for NPCs. The intelligent control method for the NPCs proposed in this paper makes the actions of the NPCs natural. In this paper, the intelligent control method analyzes the situations in the game and automatically generates the action of the NPCs.
Keywords:
Non-Player-Character, Machine Learning, Finite-State-Machine, Clustering, Game AI키워드:
자율캐릭터, 기계학습, 유한상태기계, 군집화, 게임인공지능Ⅰ. 서 론
최근에는 컴퓨터 게임의 장르가 다양해졌지만, 많은 수의 게임 사용자가 주로 이용하는 게임 장르는 롤플레잉 게임과 시뮬레이션 게임 등이 대표적이다. 이러한 게임 장르는 접속자의 수에 따라 1인용 게임과 다중 사용자용 게임으로 나눌 수 있다. 다중 사용자용 게임은 다중 접속 게임이라고도 불리며, 다중 접속 게임은 다수의 사용자가 네트워크를 통해 동시에 게임을 진행한다. 이러한 다중 접속 게임에서 사용되는 게임 캐릭터는 크게 두 가지로 나뉜다[1]. 하나는 게임 사용자가 사용하는 사용자 캐릭터이고, 다른 하나는 컴퓨터가 사용하는 캐릭터인 NPC(Non-Player-Character)이다. NPC는 역할과 특성에 따라 게임 환경에서 다양하게 존재한다. NPC는 게임 사용자와 협업이나 대전을 수행하며, 게임 사용자에게 즐거움을 제공하는 요소로 사용된다.
NPC는 컴퓨터 게임뿐만 아니라 애니메이션이나 가상현실에서도 사용하며, NPC가 자주 활용되는 이유는 게임 환경의 자연스러움 때문이다[2]. 대다수의 게임 사용자는 게임을 진행하면서 게임 세계의 모든 상황이 현실과 유사하길 희망한다. 그래서 게임 개발자들은 이러한 게임 사용자의 요구에 따라 게임 환경에 적합한 NPC를 제공한다[3]. NPC는 게임에서 많은 수의 객체로 등장하는 경우가 일반적이며, 게임 환경에서 현실감을 주기 위해 활용되는 경우가 많다[4]. 예를 들면, 동물의 무리나 가상의 군중을 표현할 때 NPC를 자주 이용한다.
게임에서 대량의 객체 군집으로 나타나는 NPC를 소수의 게임 개발자가 각기 다른 NPC의 행동 특징을 모두 생성한다는 것은 매우 어려운 일이다[5]. 다중 NPC의 행동 제어에 대한 어려움 때문에 게임 개발자들은 다중 NPC의 행동 제어에 자동화를 이용한다[6]. NPC의 자동화에 가장 많이 이용하는 기본적인 방법은 유한상태기계라고 하는 FSM(Finite-State-Machine)이다.
FSM은 상태와 전이 규칙을 이용하여 NPC의 행동을 제어한다. FSM의 구성 요소인 상태(State)는 게임 환경에서 NPC가 마주하는 특정한 상황을 의미하고, 전이 규칙은 임의 상태가 발생하였을 경우 해당 상태를 해결하기 위한 행동을 의미한다. NPC의 행동 제어에 FSM을 적용하면 규칙이 명료하고 구조가 간단하다는 장점이 있다[7]. 그러나 FSM은 게임 개발자가 NPC의 행동에 대한 모든 제어구조를 결정한다는 단점이 있다[8]. 그러므로 자연현상에 맞는 NPC의 행동 제어는 매우 어렵다[9]. FSM으로 자연현상에 유사한 NPC의 행동 제어를 완성한다고 하여도, FSM은 규칙화를 기반으로 행동 제어가 됨으로써 부자연스러움이 발생한다.
FSM의 문제점을 해결하기 위해 FSM과 확률을 결합하여 NPC의 행동 제어에 활용하면 다양한 행동을 발생시킬 수 있는 장점이 있다[10]. 확률에 기반한 FSM기법은 기본적인 행동 규칙만 FSM으로 정의하고, 각 상황에서 발생하는 다양한 환경에 대한 조건에 대해 확률을 적용한다. 이와 같은 방식을 따르는 확률을 이용한 FSM은 다양한 게임 상황에서 행동의 변화를 풍부하게 만드는 장점이 있다.
게임에서 대량으로 사용되는 NPC는 컴퓨터의 자원 활용 측면에서 상당한 부담 요소이다[11]. 이러한 문제점을 해결하기 위해 게임 상황에 대한 데이터들을 클라이언트 컴퓨터에 저장하기도 한다[12]. 방대한 게임 데이터는 게임 서버에게도 무리이기 때문에 클라이언트 컴퓨터를 활용하는 것이다.
다중 NPC의 컴퓨터 연산 부담을 완화하는 하나의 방법은 가시성검사이다. 가시성검사는 게임 사용자가 바라보는 시각으로 게임 환경을 구축하는 것이다. 게임 사용자 중심의 관점을 게임 환경에 적용하면 컴퓨터의 물리적 부하를 줄일 수 있는 장점이 있다. 가시성검사가 적용된 게임 환경에서는 다중 NPC가 필요한 게임 상황인 경우라도 게임 사용자의 시각에 나타나지 않는 NPC라면 행동을 중지시킴으로써 게임 서버의 부담을 줄일 수 있다.
게임에서 NPC의 행동 제어뿐만 아니라 게임 환경에 대한 구조도 게임 서버에 많은 부담을 준다. 현실감을 실현하기 위해서는 게임 환경을 실세계와 가깝게 정확히 묘사해야 한다. 이러한 정밀한 묘사는 데이터의 크기를 증가시켜 게임 서버에 물리적 부담을 준다. 게임 환경에 현실감을 주기 위해서는 지형이나 지물의 표현에 세밀함이 요구된다. 정밀한 지형을 묘사하기 위해서는 기본적으로 지형을 구성하는 기본 구조체가 작아지게 된다. 일반적으로 지형이나 지물을 표현하는 구조체는 그리드(Grid) 방식이다. 그리드 방식은 지형을 격자 모양으로 만들어 구조화시킨다. 지형을 세밀화하기 위해서는 레스터(Raster) 효과를 낮춰야 함으로써 그리드의 크기를 매우 작아진다. 그리드의 크기가 작아지면 지형이나 지물의 정교함은 증가되어 현실성을 높일 수 있는 장점이 있다. 그리드는 NPC들이 이동할 때 사용하는 맵(Map)의 역할도 수행한다. 동일한 크기의 맵이라도 맵을 구성하는 그리드의 크기가 작아지면 이동할 맵 타일이 증가하는 것이다. 맵 타일의 증가는 NPC가 특정 목적지로 이동할 때 증가한 맵 타일만큼 탐색량이 증가한다는 이차적 문제를 발생시킨다.
그리드 방식의 문제점을 해결할 수 있는 하나의 방법은 웨이포인트(Waypoint) 방식이다. 웨이포인트 방식은 NPC가 이동할 수 있는 위치를 미리 설정한다. 웨이포인트 방식을 사용하면 NPC는 이동을 수행할 때 맵 타일을 사용하지 않기 때문에 빠르게 경로 탐색을 수행할 수 있는 장점이 있다. 웨이포인트 방식을 채택하면 게임 서버의 하드웨어적 부담을 경감시킬 수 있는 장점이 있다. NPC의 이동에 웨이포인트 방식을 적용하면 이동에 대한 제어는 간단하지만, 웨이포인트를 따라 움직이는 NPC의 행동은 자연스럽지 못하다는 단점이 있다. 게임에서 현실감을 나타내기 위해서는 정확하고 세밀한 환경에 대한 묘사가 필요하지만, 게임 환경에서 정밀성은 게임 내에 포함된 구조물의 데이터 증가와 연결된다. 또한 많은 수량의 NPC 이동에 게임 서버는 많은 연산을 처리해야 하는 문제가 발생한다.
그리드 방식은 3차원 공간으로 표현된 게임에서는 더욱 큰 문제점을 발생시킨다. 격자 모양의 그리드를 이용하여 3차원 지형이나 지물을 구성하게 되면 2차원 지형이나 지물보다 더 많은 수의 그리드가 필요하기 때문이다. 이러한 문제를 해결하기 위해서 이동망(Navigation Mesh) 방식을 사용하면 효과적이다. 이동망의 기본 구조는 삼각형이다. 삼각형은 사각형보다 변의 수가 적기 때문에 사각형보다 공간표현이 자유롭다. 3차원 게임에서는 2차원 게임보다 NPC의 이동에 대한 탐색 타일이 증가하기 때문에, 3차원 게임에서 이동망 방식을 채택하면 그리드 방식보다 이동에 사용하는 타일의 탐색량을 줄일 수 있는 장점이다[13].
게임에서 자연스러움은 지형과 지물의 구체화 표현에 문제를 발생시키기도 하고, 대량의 NPC에게도 탐색이라는 문제를 발생시킨다[14]. 이러한 데이터 처리와 연산 처리에 대한 문제를 완화하기 위해서는 NPC의 자연스러운 행동 제어를 위해 연산량을 줄여야 할 것이다. 본 논문에서 제안한 소속도를 이용한 지능 제어법은 NPC의 특성을 나타내는 속성들을 이용하여 NPC 자신의 집단을 빠르게 찾을 수 있는 장점이 있다. 일반적으로 무리에서 이탈된 NPC는 자신의 무리를 찾기 위해 많은 연산을 요구하지만, 소속도를 이용한 지능 제어법은 유사한 무리를 쉽고 빠르게 찾을 수 있도록 함으로써 NPC 자신의 소속 집단을 찾는데 적은 연산량을 사용하는 장점이 있다. 또한 NPC의 행동 제어를 자연 현상에 위배되지 않도록 함으로써 자연스러운 움직임을 표현할 수 있다.
Ⅱ. NPC의 행동 제어
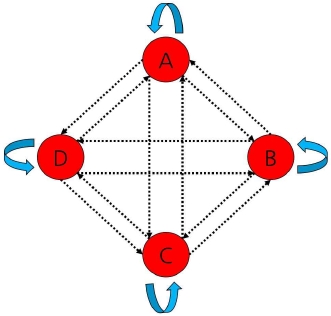
유한상태기계라고 하는 FSM 방법은 NPC의 행동을 결정하고, 특정 상태가 발생하였을 경우 상태를 해결할 전이 규칙을 제공한다. 전이 규칙은 If-Then 방식을 취하여 행동을 정의한다. FSM의 기본적인 구조를 그림 1에 나타냈다. FSM의 기본적인 시스템 구조는 그래프 방식을 따른다. 그림에 나타난 정점은 NPC가 만나는 특정 상태이다. 정점이 의미하는 상태를 예로 들면 NPC가 피식자를 만났을 상황이라 할 수 있다. 방향성이 나타난 간선은 상태의 전이 규칙을 의미한다. NPC가 피식자를 만난 상태라면 전이 규칙은 If-Then 규칙에 의해 NPC의 상태를 검사한 후에 행동을 결정한다. NPC가 굶주린 상태인지 먹이가 필요없는 상태인지를 검사한 후, 굶주린 상태의 NPC라면 피식자에게 빠르게 다가가는 행동 규칙을 생성한다. 이와 같은 절차에 의해 피식자를 만난 상태는 공격 상태로 전환된다. 이러한 상태의 변화가 전이 규칙을 적용한 것이다. FSM을 사용하면 구조가 간단하고 명료하다는 장점이 있다. 그러나 NPC의 모든 행동 규칙을 게임 개발자가 담당한다는 업무적 부담이 크고, FSM을 적용한 NPC는 규칙화된 행동 제어가 자연스럽지 못하다는 단점이 있다.
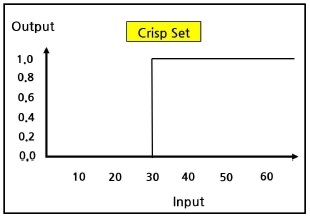
FSM의 규칙화 문제로 발생하는 부자연스러움에 확률을 적용함으로써 자연스러움을 생성할 수 있다. FSM의 전이 규칙은 크리스프 집합과 같이 불리언(Boolean) 상태로 결과를 생성한다. 그림 2에 크리스프(Crisp) 집합을 나타냈다. 그림 2에 나타난 것과 같이 입력에 해당하는 X축은 NPC의 배고픔을 나타내는 정도라 가정하면, X축은 NPC가 마주한 상태에서의 속성값에 해당한다. 출력에 해당하는 Y축은 특정 상태에서의 상태 입력값에 따른 출력으로, NPC의 행동 결정값에 해당한다.
포식자 NPC가 피식자를 만나는 상황이 발생하면 NPC는 X축의 상태 입력값을 입력 받는다. 그림 2에 따라 포식자 NPC는 배고픈 속성이 x=30이므로 전체 배고픈 정도의 최대값을 60이라 가정하면 보통에 해당하는 배고픔이다. 이와 같은 입력 상태에 대한 출력값은 y=1에 대응함으로 포식자 NPC는 피식자를 공격한다. 이러한 상태로 본다면 NPC가 배고픔 속성이 중간인 x=30 이상이면 무조건 피식자를 공격해야 한다. 이러한 상황은 다중 NPC의 집단 제어에 문제를 발생한다. 예를 들면, 배고픔 속성이 중간인 x=29이고 체력 속성이 낮은 상태일 경우에도 NPC는 피식자를 절대 공격하지 않는다. 그림 2에서 보는 바와 같이 상태에 대한 입력 속성이 x=29이면 상태에 대한 출력값은 y=0이 되기 때문에 NPC는 피식자를 공격하지 않는다. 이러한 상황을 게임이나 가상현실을 사용하는 사용자가 마주한다면 부자연스러운 현상에 어색함을 느낄 것이다.
그림 2를 이용한 동일한 상태에서 FSM에 확률기법을 적용하면 결과는 다양하게 생성될 수 있다. NPC가 피식자를 만나는 상황에서 NPC의 상황 속성 중에 배고픔 정도가 x=30이고, 체력 속성이 최하라면 그림 2에 보는 바와 같이 Y축에 상태 출력값이 y=0.0에 해당할 수도 있기 때문에 공격을 수행하지 않는다. 체력이 최저 상태인 NPC가 피식자에 대한 공격이 실패하면 체력이 고갈되어 자연사할 수 있다. 그러므로 NPC는 체력에 따라 성공 확률이 낮은 공격은 수행하지 않는 것이 자연스러운 행동이다. 확률을 이용한 FSM은 FSM보다 자연스러운 생태계를 표현한다. FSM에 확률을 사용하면 포식자 NPC가 피식자 NPC를 만난 상태에서 배고픔 정도가 x=30이라 하여도 그림 2에서 보는 바와 같이 상태에 대한 출력값을 [0.0-1.0]을 이용함으로써 NPC 상태에 따라 다양한 공격도를 나타낼 수 있는 장점이 있다. 이러한 상태에 대한 출력의 다양성은 자연생태계의 질서와 유사함을 나타내어 게임 환경을 더욱 자연스럽게 만든다.
Ⅲ. 소속도를 이용한 지능 제어
집단 이동과 같이 많은 수의 NPC가 동시에 동작을 수행하면 컴퓨터시스템에 많은 부하가 발생한다. 이러한 문제점을 해결하기 위해 본 논문에서는 소속도기반 지능 제어법을 제안한다.소속도기반 지능 제어법은 NPC의 특성을 고려하여 서로 다른 NPC와의 소속도를 측정하고, 소속도에 따라 NPC를 집단화하여 NPC의 이동에 활용한다. 동일한 무리에서는 대표 NPC가 결정되고, 대표 NPC보다 낮은 소속도를 갖는 NPC들은 대표 NPC를 따르는 일정한 행동만 유지함으로써 무리 전체에 해당하는 NPC의 다양한 행동을 생성하지 않는다는 장점이 있다.
생물학적 특징에 따라 종이 같은 동일 집단에 소속된 NPC들은 유사한 행동 제어를 수행함으로써 생물학적 동질성을 유지한다. NPC의 속성은 다음과 같다. NPC 속성에 대한 튜플이 (α1,α2, ....,αi-1,αi,....,αn for i,n∈N)으로 구성되었다고 가정하면 NPC는 각 속성의 특성으로 NPC를 집단화할 수 있다. 소속도기반 지능 제어법에서 사용하는 소속도 함수를 식 1에 나타내었다.
동일 집단에 속하는 NPC들이라고 하여도 각 객체의 능력치는 서로 다른 것이 생물학적 생태계이다. 이러한 생물학적 특성을 이용하여 NPC 속성에 계급도을 설정하였다. β는 NPC의 속성에 대한 계급도이며, 속성 계급도는 속성들의 강도를 나타내는 척도이다. 속성의 강도를 나타냄으로써 NPC의 특징을 강하게 나타내는지 약하게 나타내는지를 분석할 수 있으며, 계급도는 동일 집단에서 서열을 만든다. 계급도는 종이 동일한 서로 다른 NPC 집단에 특정 NPC가 소속할 가능성을 측정하는 척도로 활용된다. 동일 종을 NPC 집단이 다수 존재한다면 자신의 능력치와 비슷한 집단으로 소속되는 것이 자신의 서열 유지에 효과적일 것이다. 이러한 속성 강도는 특정 집단에 소속할 때 NPC의 이동에 대한 자유도를 높일 수 있는 장점이 있다.
Npi와 Npj는 서로 다른 NPC를 의미하고 각각의 NPC는 고유의 개인화된 튜플을 소유한다. 각 속성의 집단 소속도를 측정하기 위해 각 속성의 유사성을 측정하여야 하며, 유사성 측정에 사용되는 속성은 α이다. NPC의 유사성 측정에는 각 속성의 특성값을 이용한다. 이러한 특성값 활용은 동일한 종에서 분파한 서로 다른 유사 집단에 포함될 가능성을 유지함으로써 생물학적 생태의 모방에 효과적이다.
δ는 NPC 튜플의 특성값을 의미한다. NPC는 서로 다른 개체성을 나타내므로 NPC의 고유한 특징을 유지하기 위해서는 NPC의 특성을 활용해야 한다. 동일 집단에 소속된 NPC라 하여도 공격 성향이 높은 NPC도 있고 공격 성향이 낮은 NPC도 존재한다. 이러한 생명체 고유의 특징을 NPC에 활용해야 자연 생태계의 질서를 유지하면서 자연스러운 NPC 움직임을 표현할 수 있다. δ는 NPC 속성의 크기를 나타내며, 속성의 크기는 다중적 특성도를 나타낸다. NPC는 속성이 증가할수록 행동의 종류가 많을 수 있으며, 행동의 종류가 많을수록 NPC의 생존율은 높아진다. 이러한 생존율은 NPC 집단의 유사도이나 이질도 측정에 이용한다.
θ는 NPC의 튜플에 나타난 속성 특성값이다. NPC의 속성들은 각각의 특징을 나타낸다. 속성 특성은 동일한 속성이라 하여도 해당 속성의 특징은 다양하게 나타날 수 있다. 동물의 달리기나 회전 등이 대표적인 속성의 특성이다. 동일 집단에 소속된 NPC라고 하여도 각 속성의 특징들은 다르게 나타날 수 있기 때문이다. 동일한 집단에 소속된 NPC라 하여도 자연 생태계의 질서를 유지해야 한다. 그러므로 동일 집단에 소속된 각각의 NPC들은 동일한 운동 상태를 진행하여도 어떤 NPC는 직선 형태를 기반으로 운동을 진행하고 어떤 NPC는 곡선 형태를 기반으로 운동을 진행한다. 이러한 속성의 특성은 각 NPC의 고유성에 따라 다르게 나타날 수 있으며, 이러한 고유의 속성 특성을 θ에 나타냈다. ζ는 θ의 강도를 나타내며, 강도는 NPC의 회전반경의 크기나 속도의 세기 등을 결정한다. NPC가 강도를 활용하면 속도나 회전반경의 크기를 자율적으로 결정할 수 있어 NPC의 행동을 자연스럽게 만든다. 강도를 활용함으로써 NPC들은 집단과 집단 간의 친밀도를 측정할 수 있다.
λ는 이동에 대한 공간도를 나타낸다. 공간도 특성에는 2차원적 특성과 3차원적 특성으로 나눌 수 있다. 2차원적 특성이 강한 NPC는 2차원 공간을 자유롭게 이동할 수 있지만, 공간 이동에 제한적인 NPC는 2차원 공간을 제한적으로 이용할 수 있다. 동일하게 3차원적 특성이 강한 NPC는 3차원 공간을 넓은 범위로 이동할 수 있지만, 공간도가 낮은 NPC는 공간의 이동 범위가 제한적이다. n차원적 특성을 원활히 사용하는 NPC도 이지만, 제한적으로 n차원을 사용하는 NPC도 존재함으로 n.1차원, n.2차원, n.3차원 등과 같이 동일 차원에서도 서로 다른 공간 이동에 대한 범위가 다양하게 존재한다. 공간도를 사용하면 동일 집단에서 무리 움직임을 수행할 때 집단의 위치를 자유롭게 결정할 수 있는 장점이 있다. ψ는 λ의 변화도를 나타낸다. NPC의 공간 범위는 NPC의 특성에 따라 다르게 나타난다. 이러한 공간 이동에 대한 변화도를 측정하면 NPC의 변화도에 등급을 결정할 수 있다. 이러한 변화도 등급은 NPC가 집단과 집단 간의 이동에 대한 확률적 기반을 제공한다.
소속도기반 지능 제어법은 임의의 NPC가 임의의 집단에 포함될 수 있는 소속도를 나타냄으로써 서로 다른 NPC들의 집단화를 유도할 수 있는 장점이 있다. 동일 집단에 포함된 NPC들은 각기 NPC 자체 능력치를 소유하고 있으므로 자신의 집단에서 이탈할 수도 있고 다른 집단으로 이동할 수 있다. 이러한 집단 이동이 발생할 때 NPC는 소속도기반 지능 제어법을 활용함으로 이동의 자유도를 증가시키는 장점이 있다. 본 논문에서 제안한 소속도 지능 제어법은 NPC의 생물학적 스타일과 유사한 집단에 소속할 소속도를 자율적으로 계산하여 특정 집단에 소속됨으로써 자연 생태계 질서를 유지하면서 NPC의 움직임 표현이 자연스럽다.
| (1) |
자연환경 입장에서 생물의 다양성은 크게 생물의 종과 유전적 특성 등으로 구분할 수 있다. 자연환경을 생태계로 구분하면 크게 수생태계와 육상생태계로 나뉘고, 수생태계와 육상생태계는 환경에 따라 다시 세분화된다. 생물은 이러한 생태계를 기반으로 환경에 적응하며 생명을 유지한다. 생태계의 다양성에 따라 생물의 종은 세분화되며, 유전적 요인이나 환경에 대한 적응도에 따라 생물의 종은 다시 세분화된다. 생태계에 나타난 생물의 다양성은 각 생물에게 생명 유지에 효과적인 고유의 특성을 유지하지만, 생태계에 존재하는 모든 생물 개체군은 먹이사슬에 노출된다. 먹이사슬은 생물 개체군의 서열을 나타내고, 먹이사슬은 1차 생산자부터 최상위 포식자까지를 포함한 피라미드구조이다. 먹이사슬에 의해 모든 생명 개체군은 생명 활동을 유지한다.
게임 환경에서도 이러한 자연생태계의 모습처럼 생물의 종의 다양성과 먹이사슬 관계가 유지되어야 현실적이다. 게임 환경에 포함된 NPC도 게임이라는 세계에서 자연스러운 생명 활동이 표현되어야 현실감이 높아질 것이다. 본 논문에서 제안한 소속도 지능 제어법은 게임 환경에서 사용되는 NPC에게 생물학적 개체 특징을 활용할 수 있게 함으로써 자연스러운 움직임을 자동으로 생성할 수 있는 장점이 있다.
Ⅳ. 실험결과
4-1 실험환경
실험 데이터는 자연현상을 모방하기 위해 NPC의 특성을 다양하게 포함한다. 실험 데이터는 NPC 특성을 다양하게 나타내기 위해 1,000개의 개별 속성을 생성하였으며, 개별 속성은 100개의 영역 속성에 포함된다. 100개의 영역 속성은 10개의 등급 속성에 포함된다. 영역 속성에 포함된 속성들은 특정 행동에 대한 동일 종류에 해당하는 속성 집합이다. 영역 속성에 포함된 10개의 등급 속성은 동일 종류의 행동 특성에 대한 등급을 나타낸다. 동일 종류의 행동 특성에 대해 서로 다른 10개의 등급을 생성한 이유는 동일 행동이 발생하여도 NPC의 능력치는 서로 다르게 나타나기 때문이다.
영역 속성은 NPC의 특정 행동을 나타내며, 각 영역 속성은 영역 간의 유사성이 표현된다. 영역 속성에 유사성을 표현한 이유는 생물의 유전적 분류를 데이터에 포함하기 위해서다. 다양한 생물의 종을 NPC에 표현하기 위해 NPC의 행동을 나타내는 튜플의 수는 1,000,000로 설정하였다. 많은 수의 NPC 튜플을 사용한 이유는 자연계에는 많은 생물이 존재하기 때문이다. 튜플은 생물 개체군의 동질적 행동 특성을 포함하기 때문에 무리를 형성하기도 한다. 이러한 생물 개체군의 특성을 NPC에 포함하기 위해 대량의 NPC 튜플을 생성하였다. NPC의 행동 특성을 나타내는 튜플은 100개의 속성을 포함한다. 100개의 행동 속성은 NPC가 취할 수 있는 서로 다른 행동이다. 튜플에 포함된 행동 속성은 10개의 등급으로 나뉜다.
NPC의 튜플 구조에 대한 함수를 예를 들어 설명하면 다음과 같다. NPC의 행동 속성을 n이라 가정하고, 각 속성에 대한 등급 속성을 m이라 가정한다. 행동 속성에 대한 집합을 X라 가정하고, 등급 속성에 대한 집합을 Y라 가정한다. 집합 X와 집합 Y는 순서집합(Ordered set)라 가정한다. 이 때 X 집합은 속성을 나타내는 집합으로 100개의 속성을 원소로 갖는다. X 집합의 구조를 간단히 표현하면 X={αi|α1,α2,...,αi-1,αi,...,αn-1,αn for i∈N)이다. Y 집합은 등급을 나타내는 집합으로 100개의 속성을 원소로 갖는다. Y 집합의 구조를 간단히 표현하면 Y={ωi|ω1,ω2,...,ωi-1,ωi,...,ωm-1,ωm for i∈N)이다. 전제에 의해 집합 X에서 집합 Y로의 함수가 f라 가정하면, X는 정의역 집합이고 , Y는 공변역 집합이다. 튜플 구조에 대한 함수를 f라 가정하면 튜플 구조의 함수식은 y = f(x)이다. 이 때 함수 f에 대한 집합 X에서 집합 Y로의 대응 규칙은 순서집합의 순서를 유지하고, 함수 f는 one-to-one 함수이다.
NPC의 행동 속성에 대한 튜플 생성은 생태계에서 유지되는 종의 다양성을 확보하기 위해 속성 상수 ohm를 사용하였고, 속성 상수는 식 2를 이용하여 자동 생성한다. 식 2는 시그모이드(Sigmoid) 함수를 기반으로 사용하여 생태학적 모델을 생성하였다. 시그모이드 함수를 활용한 이유는 종의 탄생은 초기에 지수함수의 특성과 같이 빠르게 증가하지만, 종의 안정기에는 로그함수의 특성과 같이 느리게 증가하기 때문이다. 자연환경에 적합하도록 NPC의 속성 상수 생성에 시그모이드 함수를 이용하였으며, 시그모이드 함수에 NPC의 등급을 상수로 사용함으로써 NPC 등급에 따른 생존율을 빠르게 결정하여 자연스러운 움직임을 보장한다. 이러한 방법에 따라 적은 연산량으로 NPC의 행동을 제어함으로써 게임 서버의 물리적 부담을 줄일 수 있는 장점이 있다.
NPC의 속성 상수 Ω의 최대값은 ρ이고 최소값은 η다. 식 3에서 속성 상수의 최대값을 계산하는 함수를 나타냈고, 식 4에서 속성 상수의 최소값을 계산하는 함수를 나타냈다. Ck는 NPC의 기본 속성 상수에 해당한다. Npi는 생물 종에 포함된 NPC 객체를 의미한다. DNpi는 NPC인 Npi의 등급에 해당하는 등급 상수이다. Domain은 영역에 해당하는 영역 상수이다. 영역 상수는 영역의 레벨을 나타낸다. Int 함수는 π을 이용하여 가중치 상수를 생성한다. 가중치는 NPC의 등급이 높을수록 높은 값을 취한다. 그러므로 속성 상수의 최대값은 NPC의 등급이 높을수록 큰 값을 소유한다. 속성 상수를 높게 소유하면 NPC의 속성 수량이 증가하여 생존력이 높아질 수 있다. 이러한 구조를 따르는 이유는 생태계에서 포식자와 피식자의 먹이사슬 관계가 피라미드 구조를 이루기 때문이다.
| (2) |
| (3) |
| (3) |
실험에 사용한 집합은 Dataset1 집합과 Dataset2 집합 그리고 Dataset3과 Dataset4 집합이다. Dataset1 집합은 전체 NPC 튜플의 10%를 포함하고, Dataset2 집합은 전체 NPC 튜플의 30%를 포함한다. Dataset3는 집합은 전체 NPC 튜플이 50%를 포함하고, Dataset4 집합은 전체 NPC 튜플의 10%를 포함한다. Dataset4는 NPC의 생존율 실험에 포함되지 않고, 새로운 종의 출현을 위해 전체 실험 데이터의 감소에 따라 실험환경에 삽입되는 NPC 튜플 집합이다. 이와 같이 다양한 실험 집합을 생성한 이유는 NPC의 수량에 따른 NPC 제어기법의 특성을 측정하기 위해서다.
실험에 사용한 NPC의 행동 제어기법은 세 가지로 나뉜다. Fmethod는 유한상태기법을 적용한 NPC이고, Pmethod는 확률기법을 적용한 NPC이며, Mmethod는 본 논문에서 제안한 소속도기법을 적용한 NPC이다. 성능 측정은 NPC의 생존율을 사용하였으며, 생존율 측정에는 적중률을 이용하였다. 적중률은 전체 NPC에서 생존한 NPC의 수량을 계산하는 방식을 따른다. 실험환경을 고려해 5회 교차검증을 사용하여 실험 데이터의 불완전성을 완화하였다.
4-2 실험분석
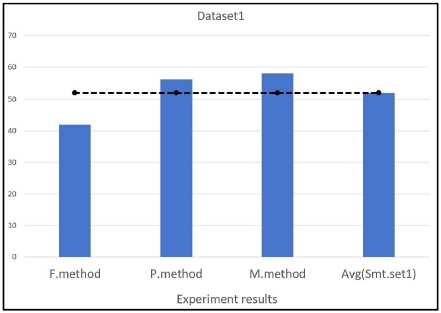
가장 적은 튜플을 포함한 Dataset1에서 유한상태기법은 42%의 생존율을 나타냈고, 확률기법은 56%의 생존을 나타내어 확률기법이 유한상태기법보다 14% 높게 나타났다. 이러한 결과가 나타난 이유는 유한상태기법은 규칙의 정형화로 집단 형성에 어려움이 발생했기 때문이다. 확률기법은 적은 튜플이지만 상황을 확률적으로 접근함으로써 집단화가 잘 표현되어 유한상태기법보다 높은 결과를 나타냈다. 소속도기법은 58%의 생존율을 나타내어 유한상태기법보다 16%로 높게 나타났고, 확률기법보다는 2% 높게 나타났다. 소속도기법은 NPC의 특성을 분석하여 집단화를 이루기 때문에 가장 높은 생존율을 보였다. 그러나 확률기법과 성능 차이가 크게 나타나지 않은 이유는 NPC 튜플 수량이 적기 때문에 NPC의 특성을 명확히 할 수 없기 때문이다. NPC의 튜플이 적을 경우 확률기법도 효과적으로 NPC의 행동 제어에 사용할 수 있다는 것을 본 실험으로 확인하였다.
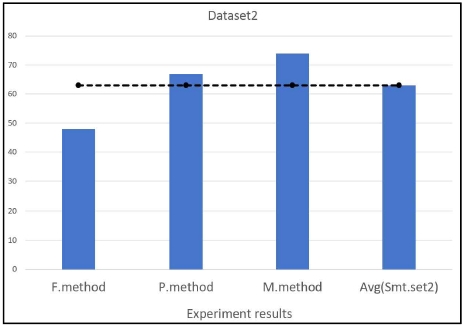
Dataset2는 Dataset1의 NPC 튜플보다 많은 수량을 포함하고 있는 데이터 집합이다. 본 실험에서 유한상태기법의 생존율은 48%를 나타내어 최소 튜플을 포함한 Dataset1에서 나타난 생존율보다 6% 높게 나타났다. 유한상태기법이 튜플의 수량이 증가함에 따라 생존율이 높아졌다. 이러한 이유는 NPC의 수량이 늘어남에 따라 동일 집단의 크기가 커짐으로 집단 생존력이 높아졌기 때문이다. 확률기법은 67%의 생존율을 나타내어 소용량 데이터 집합에서의 생존율보다 11% 높게 나타났다. 확률기법은 튜플의 수량이 증가함에 따라 확률에 이용되는 정보가 추가되기 때문에 높은 성능 향상을 나타낸 것이다. 이러한 이유로 확률기법은 유한상태기법보다 19% 높은 생존율을 나타냈다. 소속도기법은 74%의 성능을 나타내어 최소 데이터 집합에서의 생존율보다 16% 높은 결과를 나타냈다. 소속도기법은 확률기법보다 7% 높은 성능을 나타냈지만, 큰 성능 차이를 나타내지는 않았다. 소속도기법은 튜플의 수량이 증가함에 따라 NPC의 특성을 구체화하여 높은 성능 향상을 나타냈다.
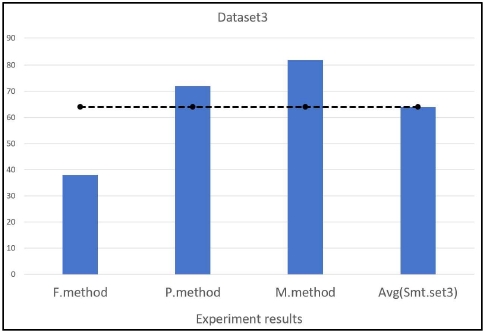
Dataset3는 가장 많은 튜플을 포함한 실험 데이터이며, Dataset3에서 유한상태기법은 38%의 생존율을 나타내어 Dataset2의 생존율보다 10% 낮게 나타냈다. 이러한 결과가 나타난 이유는 유한상태기법은 NPC의 행동 제어가 정형화되었기 때문에 다양한 종들이 존재하는 환경에서 NPC가 상황에 적절히 적응하지 못하였기 때문이다. 이러한 이유에서 대규모 튜플에서는 유한상태기법은 성능이 하락하였다. 확률기법은 72%의 생존율을 나타내어 중용량 데이터에서의 생존율보다 5% 높게 나타났다. 확률기법은 튜플의 속성에 대한 확률값을 이용하기 때문에 튜플이 일정 수준을 넘는 경우 확률값의 변화가 크지 않다는 특징이 있다. 이러한 이유에서 확률기법은 대용량 데이터 집합에서 큰 성능 향상을 나타내지 못하였다. 소속도기법은 82%의 생존율을 나타내어 중용량 데이터에서의 생존율보다 8% 높게 나타났다. 소속도기법은 NPC의 행동 특성을 고려하여 집단화를 이루기 때문에 NPC의 튜플이 증가함에 따라 안정적인 성능 향상을 나타냈다. 소속도기법은 확률기법보다 10% 높은 성능을 나타냈으며, 이러한 결과를 보더라도 소속도기법은 데이터의 크기가 커짐에 따라 NPC의 특성을 다른 기법보다 잘 정의한다는 것을 실험을 통해 확인하였다.
Ⅴ. 결 론
유한상태기법은 NPC의 행동 제어에 규칙화를 수행하여 구조가 간단하다는 장점이 있으나, 게임 개발자가 NPC의 모든 제어구조를 결정해야 한다는 단점이 있다. 실험에 유한상태기법은 소량의 데이터 집합에서는 잘 적응하였으나, 데이터 집합의 크기가 증가함에 따라 생존율이 낮아지는 것을 실험을 통해 확인하였다. 유한상태기법은 행동 제어의 일반화된 규칙 때문에 이러한 결과를 나타낸 것이다.
확률기법은 NPC의 속성에 대한 확률을 이용하여 집단화를 수행하며, 이러한 방식을 취하게 되면 다양한 상황에서 효과적으로 집단화를 이룬다. 소량의 데이터 집합에서 확률기법은 우수한 결과를 나타냈으며, 데이터의 크기가 커짐에 따라 안정적 성능을 유지하였다. 그러나 대용량 집합에서는 성능 향상이 크지 않았다. 이러한 결과가 발생한 이유는 속성에 대한 확률기법은 데이터의 크기가 커짐에 따라 동일 속성의 수량이 증가해야 높은 정확도를 나타낼 수 있는데, 대규모 NPC가 존재하는 상태에서는 데이터의 수량이 증가함에 따라 NPC의 종류도 증가하기 때문에 높은 정확도 향상이 나타나지 않았다.
본 논문에서 제안한 소속도기법은 소량의 데이터에서 다른 기법에 비해 우수한 성능을 나타냈으며, 데이터의 수량이 증가함에 따라 안정된 성능을 유지하였다. 소속도기법은 NPC 속성의 소속도를 이용하여 집단화를 자율적으로 생성하는 특성이 있다. 속성에 대한 소속도를 이용하면 NPC의 특성 구분이 쉬워진다는 장점이 있으며, 빠른 소속도 생성은 게임 서버의 물리적 부하를 줄여주는 장점도 있다. 이러한 이유에서 소속도기법은 다양한 실험에서 우수한 결과를 나타냈다.
References
- P. Gomes and A. Jhala, “AI authoring for virtual characters in conflict,” in Proceeding of the 9th AAAI Conference on Artificial Intelligence, pp. 130–141, 2013.
- A. Coman and H. Munoz-Avila, “Plan-based character diversity,” in Proceeding of the 8th AAAI Conference on Artificial Intelligence, pp. 118– 123, 2012.
-
S. Samothrakis, D. Perez-Liebana, P. Rohlfshagen, and S. M. Lucas, “Predicting dominance rankings for score-based games,” The Journal of IEEE Transactions on Computational Intelligence and AI in Games, Vol. 8, No. 1, pp. 1–12, Mar. 2014.
[https://doi.org/10.1109/TCIAIG.2014.2346242]

-
D. Perez-Liebana et al., “The 2014 General Video Game Playing Competition,” The Journal of IEEE Transactions on Computational Intelligence and AI in Games, Vol. 8, No. 3, pp. 229–243, 2016.
[https://doi.org/10.1109/TCIAIG.2015.2402393]

-
D. Masad and J. Kazil, “MESA: an agent-based modeling framework,” in Proceeding of the 14th PYTHON Conference on Science, pp. 53–60, 2015.
[https://doi.org/10.25080/Majora-7b98e3ed-009]

-
K. Merrick, "Intrinsic motivation and introspection in reinforcement learning," The Journal of IEEE Transactions on Autonomous Mental Development, Vol. 4, pp. 315-329, 2012.
[https://doi.org/10.1109/TAMD.2012.2208457]

- M. Johansson and H. Verhagen, “Social believability in games—the early years,” in Proceeding of the 9th Social Believability Games Workshop on Digital Games, pp. 141–146, 2014.
- J. Laird and M. van Lent, "Interactive computer games: human-level AI's killer application," in Proceeding of the AAAI Conference on Artificial Intelligence, pp. 1171-1178, 2000.
- D. Perez-Liebana, S. Samothrakis, J. Togelius, S. M. Lucas, and T. Schaul, “General video game AI: Competition, challenges and opportunities,” in Proceeding of the 30th AAAI Conference on Artificial Intelligence, pp. 4335–4337, 2016.
-
Zhang Jiuyong et.al., “The mathematical model based on the battle of Berlin”, in Proceeding of the 8th IEEE Conference on Fuzzy Systems and Knowledge Discovery, pp. 121–124, 2011.
[https://doi.org/10.1109/FSKD.2011.6020037]

-
C. Browne and F. Maire, “Evolutionary Game Design,” The Journal of IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 1, pp. 1-16, March 2010.
[https://doi.org/10.1109/TCIAIG.2010.2041928]

-
S. Bakkes, P. Spronck, and J. van den Herik, “Rapid and reliable adaptation of video game AI,” The Journal of IEEE Transactions on Computational Intelligence and AI in Games, Vol. 1, No. 2, pp. 93–104, Jun. 2009.
[https://doi.org/10.1109/TCIAIG.2009.2029084]

-
R. Prada, P. Lopes, J. Catarino, J. Quitrio, and F. S. Melo, “The Geometry Friends Game AI competition,” in Proceeding of the IEEE Conference on Computational Intelligent Games, pp. 431–438, 2015.
[https://doi.org/10.1109/CIG.2015.7317949]

- J. McCoy, “Prom week: Designing past the game/story dilemma,” in Proceeding of the 8th International Conference on Digital Games, pp. 94–101, 2013.
저자소개

2001년 : 동국대학교 컴퓨터공학과 (공학석사)
2004년 : 동국대학교 컴퓨터공학과 (공학박사)
1996년~1998년: (주)경기은행
2005년~2006년: 동국대학교 컴퓨터공학과 IT교수
2007년~2018년: 나사렛대학교 IT융합학부 교수
2019년~현 재: 명지대학교 융합소프트웨어학부 객원교수
※관심분야:인공지능(Artificial Intelligence), 빅데이터(Big Data), 의료정보(Medical Information), 기계학습(Machine Learning), 자율이동로봇(Autonomous Mobile Robot), 게임인공지능(Game AI) 등

1999년 : 동국대학교 컴퓨터교육 (교육학석사)
2009년 : 동국대학교 정보통신공학과 (공학박사)
1996년~1999년: ㈜유니파이코리아
2001년~현 재: 한국폴리텍대학 인천캠퍼스 컴퓨터정보과 교수
※관심분야:인공지능(Artificial Intelligence), 의료정보(Medical Information), 빅데이터(Big Data), 정보검색(Information Retrieval) 가상교육(Virtual Education), 게임인공지능(Game AI), 증강현실(Augmented Reality) 등