[ Article ]

Journal of Digital Contents Society - Vol. 21, No. 9, pp.1567-1573

ISSN: 1598-2009 (Print) 2287-738X (Online)

Print publication date 30 Sep 2020

Received 20 Aug 2020 Revised 14 Sep 2020 Accepted 14 Sep 2020

DOI: https://doi.org/10.9728/dcs.2020.21.9.1567

Design and Implementation of Basketball Game Content based on Unity Game Engine and Android Platform

Sung-Yun Kang¹ ; Ki-Hong Park²^{, *}

1Team Leader, R&D Lab, MediaWork CO. LTD, Daejeon 31487, Korea
2Professor, Division of Convergence Computer & Media, Mokwon University, Daejeon 35349, Korea

유니티 게임 엔진과 안드로이드 플랫폼 기반의 농구 게임 콘텐츠 설계 및 구현

강성윤¹ ; 박기홍²^{, *}

1(주)미디어워크 연구개발팀 팀장
2목원대학교 융합컴퓨터미디어학부 교수

Correspondence to: ^*Ki-Hong Park Tel: +82-42-829-7639 E-mail: kihong@mokwon.ac.kr

Copyright ⓒ 2020 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this paper, we designed a mobile basketball game based on the android platform, and implemented the contents using the unity game engine. A proposed basketball game contents consisted of three types: confrontation, arcade, and last ball, and physical forces such as parabolic and free fall motion were applied to enhance the realistic implementation and a realism of the basketball trajectory. In particular, the physical forces implemented for realism were the distance between the shooting point and the goal-in point on the plane, the time of free fall, and velocity in the horizontal and vertical directions. As a result of implementation, it was confirmed that the principle of the designed physical force is operated according to the design standard, and the basketball trajectory was naturally displayed.

초록

본 논문에서는 안드로이드 플랫폼 기반의 모바일 농구 게임을 설계하고, 유니티 게임 엔진을 이용하여 콘텐츠를 구현하였다. 제안하는 농구 게임 콘텐츠는 대결, 아케이드 및 라스트 볼의 세 가지 유형으로 구성하였으며, 농구공의 궤적에 대한 사실적 구현과 현실감을 높이기 위해 포물선과 자유 낙하와 같은 물리적인 힘을 적용하였다. 특히, 현실감을 위해 구현된 물리적인 힘들은 평면상의 슈팅 지점과 골인 지점 간의 거리, 자유 낙하 시간, 수평 및 수직 방향의 속도 등이 적용되었다. 구현 결과, 설계한 물리적 힘 원리가 설계 규격대로 동작하였으며, 농구공의 궤적이 자연스럽게 연출되는 것을 확인할 수 있었다.

Keywords:

Basketball game, Sport game, Mobile game, Parabolic motion, Unity game engine

키워드:

농구 게임, 스포츠 게임, 모바일 게임, 포물선 운동, 유니티 게임 엔진

Ⅰ. Introduction

From a long time ago, humans have tried to expand their experiences in reality by using various devices to show their imagination. This experience has made it possible to simulate a reality that is almost completely embodied in a digital display and even a 4D movie that stimulates the five senses [1]. In addition, as the technology of smartphones develops, these functions are becoming possible to implement, and in this trend, users who enjoy smartphone games are increasing every year as the spread of smartphones expands [2].

According to the 「2019 Global Games Market Report」 by Newzoo, a global game industry research institute, the size of the global game market for this year is growing by 9.6% compared to the previous year [3]. However, the share of sports games is not very high, and the share of global users who use sports games in the global game market also accounts for less than 10% [4][5]. This is considered to be due to the remarkable lack of completeness of games including realism in many sports games.

Therefore, in this paper, we design and implement a basketball game based on physical force in order to activate sports games, apply a sense of reality that are insufficient in existing games, and increase immersion. In this paper, a basketball game that can apply physical force within smartphone-based sports game contents is selected, and Figure 1 shows the results of a basketball game search in the Google Play Store [6].

Fig. 1.

Basketball game applications

Ⅱ. Related Theories for Basketball Game Content

This section describes theories related to parabolic and free fall motion for implementing basketball game content.

2-1 Parabolic Motion

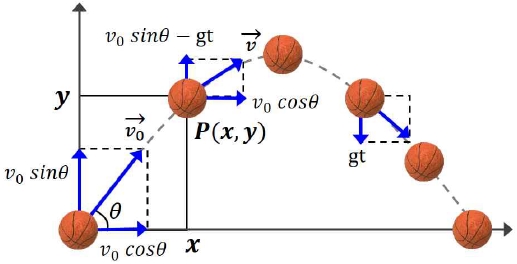
A parabolic motion refers to the motion when an object receives force in a direction not the same as the motion direction. As shown in Figure 2, the concept of parabolic motion has an initial velocity (v_ox, v_oy), and the components of the horizontal and vertical directions when the object is launched from the surface can be obtained as Equation 1.

Fig. 2.

Concept of the parabolic motion formula

v 0 x, v 0 y = v 0 cos ⁡ θ, v 0 sin ⁡ θ .

(1)

Since there is only acceleration in the vertical direction, the velocity in the horizontal direction is constant, being equal to v₀ cosθ [7]. The vertical velocity follows the free fall motion and the acceleration is constant. Therefore, the acceleration at the coordinate P(x, y) in Figure 2 has the values of 0 and –g, respectively. Here, the g, which is he value of 9.81m/s² near the surface of the earth, is the acceleration due to gravity.

The velocity at the coordinate P(x, y) does not change in the horizontal direction, and the vertical direction increases constantly by the gravity g, so it is expressed as Equation 2.

v x, v y = v 0 cos ⁡ θ, v 0 sin ⁡ θ - g t .

(2)

Also, the displacement in the horizontal and vertical directions according to time t is as shown in Equation 3 [7].

x, y = v 0 t cos ⁡ θ, v 0 t sin ⁡ θ - g t 2 / 2 .

(3)

2-2 Velocity and Displacement in Free Fall Motion

In general, the free fall motion refers to a motion in which an object falls near the surface with the gravity g. This section describes the method of obtaining the velocity and displacement values during free fall of a parabolic [8]-[10].

First, the velocity of an object with mass can be obtained by integrating the acceleration over time, and is shown in Equation 4.

v = v 0 + g t = g t .

(4)

Here, the initial velocity v₀ is a value of 0. Second, if the initial displacement is S₀, the displacement of the object can be obtained by integrating the velocity, and is shown in Equation 5.

S = S 0 + g t 2 2 .

(5)

Ⅲ. Content Design and Implementation

3-1 Content Design

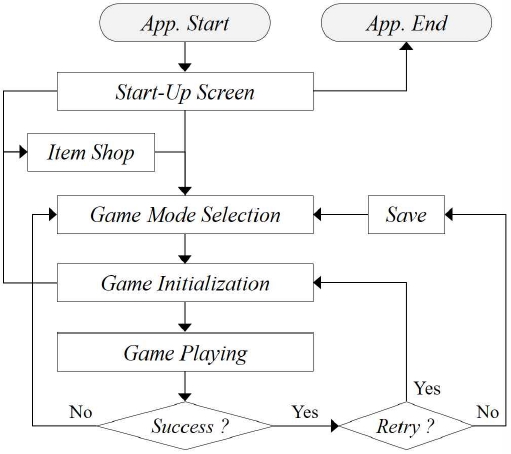
The composition and flow of the proposed basketball game content system are shown in Figure 3. The transition or flow between activities in the proposed content is similar to the flow of various mobile-based basketball game contents, but it aims to give a realism like enjoying a real basketball by applying the parabolic motion and free fall motion suggested in Section 2.

Fig. 3.

Flowchart of proposed basketball game content

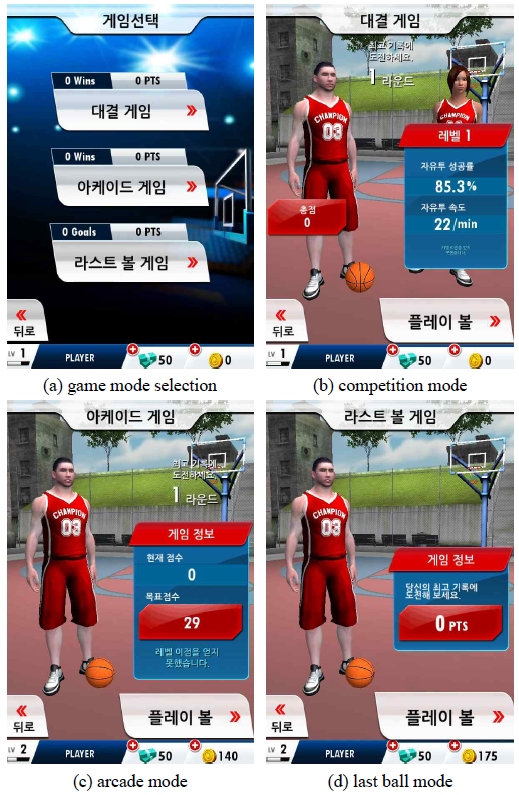
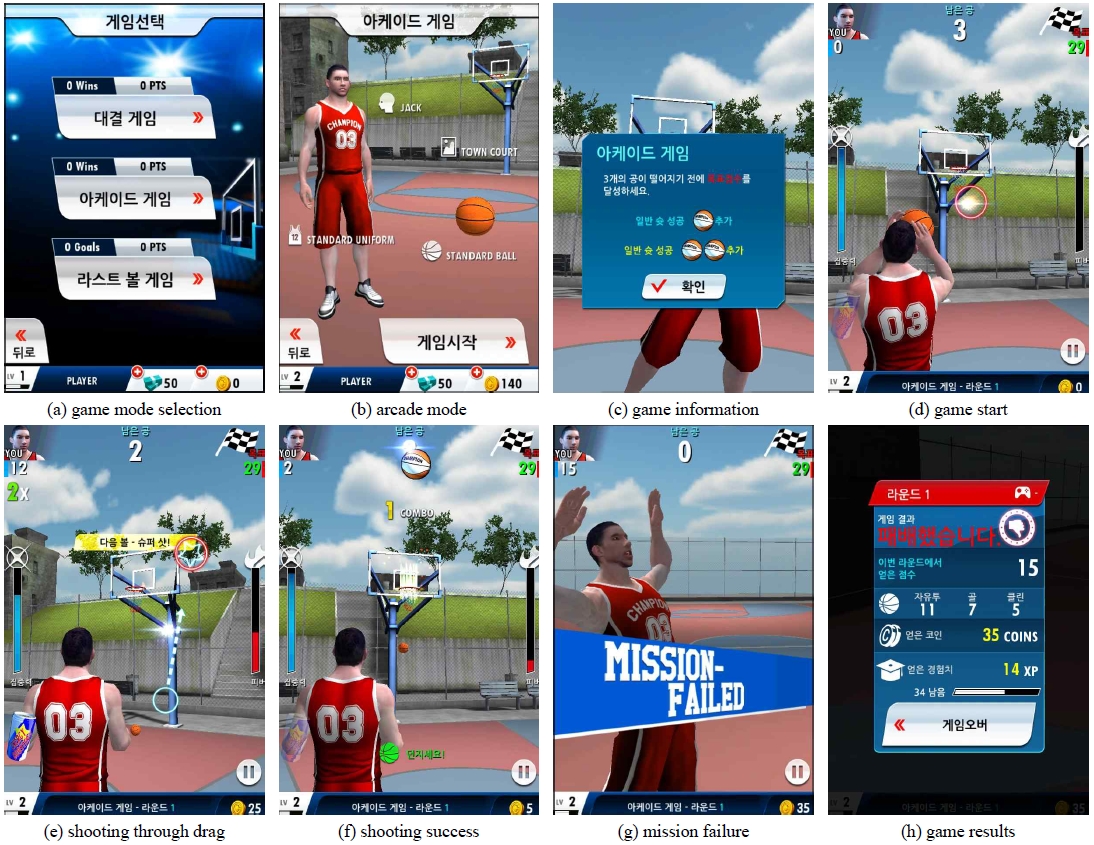
As shown in Figure 4, the proposed basketball game contents consisted of competition, arcade and last ball game modes. First, the competition mode is a game mode in which a player competes in PVE or PVP for 45 seconds, and wins if the player scores higher than the opponent. Second, the arcade mode has the following features and scenarios as a way to get a score higher than the suggested mission score with three balls.

Fig. 4.

Three game modes for basketball game content

․ Whenever the ball is not inserted, the ball decreases by one.
․ The game is over when you run out of balls.
․ If you get a score higher than the mission score, you win.
․ Mission scores increase as users keep winning streak.

Lastly, the last ball mode is a game mode in which a free throw is played with one ball, and if the free throw is successful, the game can continue. In particular, the competition and arcade games applied the winning streak system, and the level or mission score increased as the streak continued.

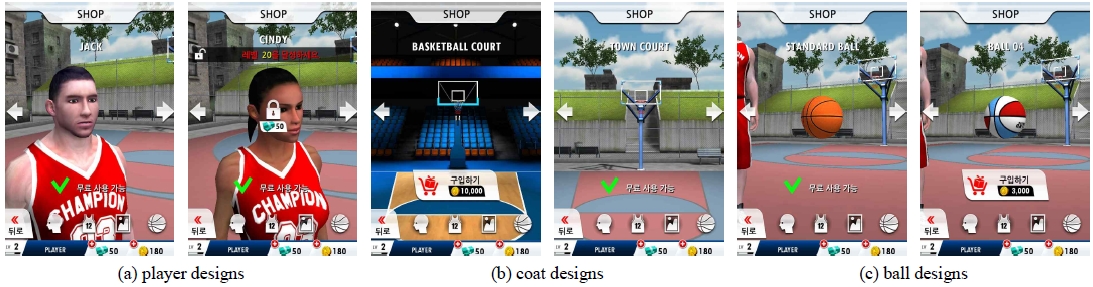
Figure 5 is the main screen corresponding to the overall flow of the basketball game content presented in Figure 3, and shows the results in the arcade mode. Shooting is carried out by dragging from the start position of the screen to a randomly generated position within the ball control time as shown in Figure 5(e). In addition, an item shop function, which can select or upgrade items such as players, uniforms, courts and balls, is implemented as shown in Figure 6 in order to increase the enjoyment and satisfaction of users. The item shop has 6 players, 15 uniforms, 2 basketball courts, and 30 balls. For each item, the ball control time, goal-in area accuracy, pivot time and experience value were applied differently.

Fig. 5.

Screens for each stage of the proposed basketball game content

Fig. 6.

Designs implemented in the item shop

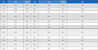
The overall flow and designs of the proposed basketball game contents described in this section were implemented within the environment presented in Table 1. In this paper, 3ds Max 2015 and Photoshop CS6 were used for the design of characters, game backgrounds, and various items as shown in Figure 6, and the game engine Unity 2019 was used for overall content design and implementation.

Table 1.

Environment for content implementation

3-2 Content Implementation for Realism

Due to the nature of the proposed basketball game, in order to throw a basketball naturally, the parabolic formula described in Section 2.1 is basically required. First, in order to create the natural trajectory of the ball, the highest position of the parabolic line must be obtained, and the point of arrival (goal-in) must be selected higher than the position of the player throwing the ball. In fact, if the shooting angle is more than 45 degrees, it does not matter to apply that height. However, if the maximum height of the parabola is fixed and the distance between the shooting point and the goal-in is gradually increasing, the firing angle will be 45 degrees or less. This can lead to an unnatural trajectory due to the abnormal ball firing speed. Therefore, when the distance is over a certain distance, the trajectory of the basketball must be naturally produced by setting the height so that the shooting angle is 45 degrees. The code for calculating the distance between the shooting point and the goal-in point on the plane is presented in Table 2.

Table 2.

Code for calculating the distance between the shooting point and the goal-in point

Second, the free fall time can be calculated as the time to reach the goal-in point using Equation 5, and can be derived as Equation 6.

S = g t 2 2, ∴ t = 2 S g .

(6)

Finally, as shown in Figure 2, the velocity in the vertical direction at the shooting point must be calculated. The velocity in the vertical direction is the same as the constant acceleration motion because only gravity acts when the resistance of air is ignored. Therefore, the free fall speed v_y is the same as the speed when it reaches the ground as shown in Equation 7.

v y = g t = g 2 S g = 2 g S .

(7)

In addition, codes for calculating the time and the velocity during free fall described in Equations 6 and 7 are presented in Tables 3 and 4, respectively. Figure 7 shows the result screens applied with the contents described in this section.

Table 3.

Code for calculating the time and the velocity during free fall

Table 4.

Code for calculating the vertical velocity during free fall

Fig. 7.

Result screens based on physical forces

Ⅳ. Conclusion

In this paper, we designed and implemented a basketball game content based on the unity game engine and android platform. The natural direction of the ball trajectory between the shooting point and the goal point should be considered as an important consideration which is implemented a basketball game content. In the proposed and implemented basketball game content, the motion of the parabola and the free fall motion are applied to the ball so that it can be experienced like a real game. The application of the physical force can increase immersion and realism. As a result of the experiment, it was confirmed that the implemented mobile basketball game operates according to the physical force-based design specifications described in section 3.2. In the future, we intend to design and implement various applications to activate sports games and increase the sense of reality that are lacking in existing games.

References

Ministry of Science and ICT and Korea Mobile Internet Business Association, 2018 Mobile Content Industry, Survey Report, 2018
E S. Gwak, “A Study on Gamers’ Game Acts and Play Time,” The Journal of Korea Game Society, Vol. 17, No. 4, pp. 71-79, Aug. 2017.
Y. B. Lee, “Preliminary research on esports of Northeast Asia part 1: Downfall of affect, 10 years history of Korean e-sports,” Journal of Korea Game Society, Vol. 20, No. 2, pp. 61-74, April, 2020.
Mobile Index: Mobile Data Intelligence, General summary of the Korean mobile game market in the first half of 2019, IGAWorks, Insight Report, 2019.
Mobile Index. Mobile game market status in the first half of 2020 [Internet]. Available: https://www.mobileindex.com/report/report_view?s=131, .
Google Play Store. Search by keyword:basketball [Internet]. Available: https://play.google.com/store/search?q=basketball, .
Wikipedia. Projectile motion [Internet]. Available: https://en.wikipedia.org/wiki/Projectile_motion#cite_note-3, .
S. Y. Kang and K. H. Park “Design and Implementation of Sleigh Game Content based on Physical Force using Unity3D Game Engine,” The Journal of Digital Contents Society, Vol. 20, No. 12, pp. 2301-2307, Dec. 2019. [https://doi.org/10.9728/dcs.2019.20.12.2301]
K. H. Park, S. Y. Kang and Y. H. Kim, “Implementation of archery game application using VR HMD in mobile cloud environments,” Advanced Science Letters, Vol. 23, No. 10, pp. 9804-9807, Oct. 2017. [https://doi.org/10.1166/asl.2017.9801]
Wikipedia. Free Fall [Internet]. Available: https://en.wikipedia.org/wiki/Free_fall, .
Unity. Unity Game Engine 2019 [Internet]. Available: https://unity.com/kr, .

Author Information

강성윤(Sung-Yun Kang)

2008: Department of IT Engineering, Graduate School of Mokwon University (M.S Degree)

2018: Department of IT Engineering, Graduate School of Mokwon University (Ph.D Degree)

2004～2010: Director in Mediawork Co., Ltd.

2010～2014: CEO in DigitalC Co., Ltd.

2014～now: Director in Mediawork Co., Ltd.

※ Research Interests: digital contents, computer vision, object oriented programming, game programming.

박기홍(Ki-Hong Park)

2005: Department of IT Engineering, Graduate School of Mokwon University (M.S Degree)

2010: Department of IT Engineering, Graduate School of Mokwon University (Ph.D Degree)

2008～2009: Researcher in Prevention of Disaster with Information Technology RIC.

2011～2012: Senior Researcher in Inconex Co., Ltd.

2012～now: Assistant Professor in Div. of Convergence Computer & Media, Mokwon University.

2014～now: Chairman of Life Safety Division in Daejeon City Association, Safety Culture Campaign.

2015～now: Sub-chairman in Daejeon City Association, Volunteer of Community Safety Monitor.

※ Research Interests: digital content, computer vision, pattern recognition, H.26x, aviation application technology, disaster prevention application technology.

Fig. 1.

Basketball game applications

Fig. 2.

Concept of the parabolic motion formula

Fig. 3.

Flowchart of proposed basketball game content

Fig. 4.

Three game modes for basketball game content

Fig. 5.

Screens for each stage of the proposed basketball game content

Fig. 6.

Designs implemented in the item shop

Fig. 7.

Result screens based on physical forces

Table 1.

Environment for content implementation

category	contents
O/S	window 7 / 10 (64bit)
S/W	Visual Studio 2017, 3ds Max 2015, Photoshop CS6
game engine	Unity 2019 [11]

Table 2.

Code for calculating the distance between the shooting point and the goal-in point

Vector3 startPosition;                     // Shooting point
Vector3 finalPosition;                     // Goal-in point
float maxHeightOffset = 0.6f;        // Correction value to select the highest position in case of close distance
float range;                                      // Distance between two points on the plane
private floatcalcMaxHeight() {
     // Calculate the distance between two points on a plane
     Vector3 direction = new Vector3(finalPosition.x, 0f, finalPosition.z) - new Vector3 (startPosition.x, 0f, startPosition.z);
     range = direction.magnitude;     // Distance between two points
     float maxYPos = finalPosition.y + maxHeightOffset;    // Common height
     if (range / 2f > maxYPos)          // If the height is lower than 45 degrees, change the height to maintain the height at 45 degrees.
          maxYPos = range / 2f;
    return maxYPos;
}

Table 3.

Code for calculating the time and the velocity during free fall

private Vector3 findInitialTimeVelocity() {
          ......
     // Time for the basketball to reach the peak
     float timeToMax = Mathf.Sqrt(-2 * (maxYPos - startPosition.y) / Physics.gravity.y);
     // Time until the ball reaches the goal-in point from the peak
     float timeToTargetY = Mathf.Sqrt(-2 * (maxYPos – finalPosition.y)/Physics.gravity.y);
     float totalFlightTime = timeToMax + timeToTargetY;
     // Calculate the distance between two points on a plane
     Vector3 direction = new Vector3(finalPosition.x, 0f, finalPosition.z) - new Vector3 (startPosition.x, 0f, startPosition.z);
     float range = direction.magnitude;     // Distance between two points
     Vector3 unitDirection = direction.normalized;
     // Velocity in horizontal direction
     float horizontalVelocityMagnitude = range / totalFlightTime;
     // Velocity distributed across each axis
     newVel.x = horizontalVelocityMagnitude * unitDirection.x;
     newVel.z = horizontalVelocityMagnitude * unitDirection.z;
     return newVel;
}

Table 4.

Code for calculating the vertical velocity during free fall

private Vector3 findInitialVelocity() {
    Vector3 newVel = new Vector3();     // Velocity
    newVel.y = Mathf.Sqrt(-2.0f * Physics.gravity.y * (maxYPos – startPosition.y));     // Vertical velocity
          ......
    return newVel;
}