유사 프로그램 분석을 위한 선형 회귀 모델의 데이터 슬라이싱 기법 연구
Copyright ⓒ 2020 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
소프트웨어의 중요성이 증가함에 따라 효율적인 소프트웨어 개발을 위한 분석 기술이 필요하며, 유사 프로그램을 분석하는 기술은 소프트웨어의 특성을 이해하기 위한 기본적인 방법이다. 본 논문에서는 유사 프로그램을 분석하기 위한 방법으로 선형 회귀를 이용한 분석 모델을 설계한다. 그리고, 노이즈로 인한 학습의 오류를 줄이고, 선형 회귀 분석 모델의 정확도를 향상시키기 위해 데이터를 분할하는 슬라이싱 기법을 적용하는 방법을 제안한다. 기존의 일반적인 선형 회귀 분석 모델과 비교 실험에서 데이터 슬라이싱을 적용한 모델은 유사 프로그램 분석 결과의 정확도가 향상된다는 것을 확인할 수 있었다. 선형 회귀 분석에서 데이터 슬라이싱을 적용하는 방법은 예측 결과의 신뢰성을 향상시키기 위해 효과적으로 적용될 수 있을 것이라 기대된다.
Abstract
As the importance of software increases, software analysis is needed for efficient software development. Analyzing similar programs is a base technology to understand the characteristics of software. In this paper, a linear regression model for analyzing similar programs is designed. Then, to reduce training errors due to noise of data, it is proposed to apply slicing techniques to separate data. In comparison experiments with the conventional linear regression model, it was found that the accuracy of the analysis results was improved in the linear regression model with data slicing. It is expected that the data slicing method can be applied to improve the reliability of the prediction results in linear regression.
Keywords:
Data slicing, Linear regression, Machine learning, Similar program analysis, Software analysis키워드:
데이터 슬라이싱, 선형 회귀, 기계 학습, 유사 프로그램 분석, 소프트웨어 분석Ⅰ. 서 론
정보 시스템에서 소프트웨어의 중요성이 증가하고 있으며, 소프트웨어 개발에 필요한 분석 기술과 소프트웨어의 특성을 이해하기 위한 노력이 필요하다. 소프트웨어가 가지는 특성을 분석하고 비교하는 기술은 소프트웨어 활용을 위해 중요한 기반 기술이 된다. 이 논문에서는 소프트웨어의 특성 정보 분석을 통해 유사 프로그램을 분석하기 위해 기계 학습을 적용하는 방법을 제시한다. 또한, 기존의 선형 회귀 분석 방법의 정확성을 향상시키기 위해 학습 데이터를 분할하는 슬라이싱을 적용하는 방법을 제안하고 유사 프로그램 분석을 위해 선형 회귀 모델에 적용한다.
소프트웨어의 특성을 이해하고 비교 분석하기 위해서는 소프트웨어의 구조를 이루는 바이너리 코드를 이해할 수 있어야 한다. 일련의 바이너리 데이터로 구성되는 소프트웨어의 형태는 직접적인 분석을 통해서 효과적이고 체계적으로 이해하기 어려운 복잡한 구조를 가지고 있다. 따라서, 소프트웨어의 분석을 위해서 복잡한 분석 알고리즘을 필요로 한다. 반면, 최근에 다양한 응용 분야에서 인공 지능 및 기계 학습 방법의 활용이 증가하고 있으며, 소프트웨어의 분석에서 기계 학습 기술을 활용해 문제를 해결할 수 있는 접근 방법에 대해 연구가 활성화되고 있다.
이 논문에서는 바이너리 코드로 구성된 소프트웨어의 유사성을 분석하기 위해서 기계 학습 방법 중에 하나인 선형 회귀 모델을 설계하고, 학습 데이터를 분할하기 위한 데이터 슬라이싱을 적용하는 방법을 제안한다. 기계 학습은 데이터로 부터의 학습 과정을 거쳐서 문제를 해결할 수 있는 모델을 생성하는 접근 방법이다. 따라서 학습에 사용하는 데이터를 효율적으로 처리하는 것이 좋은 학습 결과를 유도하는데 도움이 된다. 이 논문에서는 데이터 분할을 통해서 학습 정확도를 개선할 수 있는 방법을 설계하고, 유사 프로그램 분석을 위한 선형 회귀 모델에 적용함으로써 결과의 정확도를 개선하는 방법을 제안한다.
본 논문의 구성은 다음과 같다. 2장에서는 유사한 소프트웨어를 분석하기 위한 기존의 관련 연구들에 대해서 소개한다. 3장에서는 본 논문에서 제안하는 데이터 분할을 위한 슬라이싱 방법과 이를 적용하는 선형 회귀 모델의 설계 방법을 기술한다. 4장에서는 본 논문에서 제안한 데이터 슬라이싱 기법을 이용한 선형 회귀 모델을 평가하기 위한 비교 실험을 수행하고, 실험 결과를 보여준다. 마지막으로, 5장에서 본 논문의 결론을 맺는다.
Ⅱ. 관련 연구
소프트웨어는 정보 시스템에서 중요한 역할을 수행하기 때문에 오류 없는 소프트웨어를 개발하기 위한 다양한 분석 기술이 필요하다. 소프트웨어의 분석은 소프트웨어의 특성을 보다 잘 이해할 수 있도록 지원하며 또한 유사 프로그램을 분석 하는 기술은 기본적인 소프트웨어 분석 기술로 연구되고 있다. 프로그램의 유사성 분석은 공통 모듈 검색 [1], 저작권 위반 및 도용 탐지 [2, 3], 악성코드 탐지 [4] 등 다양한 활용 분야를 가지고 있으며 소프트웨어 분석의 기반이 되는 기술이라고 할 수 있다.
전통적인 분석에서의 유사 프로그램 분석은 소프트웨어가 가지는 특정 요소들을 데이터화하고 이를 비교하는 방법을 활용한다. [5]에서는 소프트웨어에 포함된 텍스트를 추출하고, 비교를 통해 최장 공통 부분 순서열(longest common subsequence, LCS)을 찾는 방법을 적용하고 있다. LCS는 두 시퀀스 정보에 대해서 공통된 정보가 얼마나 많은지 판단할 수 있기 때문에 유사성을 비교하기 위한 연산에서 효과적으로 적용된다. k-gram 방법 [6]은 프로그램 내에 포함된 연속된 코드 배열의 특성을 비교하는 방법이다. 소프트웨어의 동작을 위해서 소프트웨어 내에는 다수의 명령어들과 데이터들이 포함되는데, 명령어의 패턴들을 비교하고 동일한 패턴을 찾아냄으로써 프로그램의 유사성을 평가하는 기술이다. [7]에서는 소프트웨어의 구조적인 특성을 나타내는 그래프 구조를 정의하고 비교함으로써 유사성을 검출하는 방법을 제시하고 있다. 이 방법에서는 프로그램 내의 구문의 의존성 관계를 프로그램 의존 그래프로 정의하고 그래프를 비교하는 방법을 제안하고 있다. [2]에서는 프로그램이 가지는 경로를 요약하고 요약된 경로를 표현하는 전체 프로그램 경로 그래프 (whole program path graph)를 이용해서 프로그램의 실행 경로를 특성화하고 비교하는 방법을 제안하고 있다. 이와 같이 전통적인 프로그램의 유사성 분석은 프로그램에 포함된 세부 특징에 대한 분석을 통해 프로그램을 요약하고 정형화된 구조로 표현한 후 비교하는 방법이 적용된다. 이런 방법은 분석에 적용되는 프로그램의 세부적인 특징을 즉시 반영할 수 있으며, 프로그램의 개별적인 특성을 반영한 알고리즘으로 구성된다.
최근의 인공 지능 기술의 활용 범위가 증가하면서 다양한 응용 분야에서 인공 지능 및 기계 학습의 기술을 적용해서 문제를 모델링하고 해결하고자 하는 연구가 증가하고 있다. 소프트웨어의 특성을 데이터로 하는 분석 기술에서도 직접적인 분석 알고리즘을 통한 접근 방법과 더불어 기계 학습을 이용한 접근 방법에 대한 연구가 시도되고 있다. 소스 코드 표절 탐지를 위한 방법으로 n-gram 등의 특성을 분석하고 신경망을 활용하는 방법 [8, 9], 나이브베이즈 분류기와 k 최근접 이웃 알고리즘을 이용하는 방법[10] 등이 연구되었다. 또한, 바이너리 코드의 유사성 분석을 위해 코드의 이미지를 생성하고 이미지를 분류하는 딥러닝 [11]을 적용하거나 바이너리 코드의 공통 특성을 학습 데이터로 학습할 수 있는 신경망 [12]을 이용하는 방법, 서포트 벡터 머신 [13] 등이 연구되었다. 이 논문에서는 유사 소프트웨어 분석을 위한 기존의 선형 회귀 방법의 분석 정확성을 향상시키기 위해서 학습 데이터에 대해 데이터를 분할하는 슬라이싱을 적용하는 방법을 제안한다.
Ⅲ. 선형 회귀의 데이터 슬라이싱 기법
3-1 선형 회귀의 개념 및 활용
선형 회귀는 독립적인 값을 가지는 여러 개의 변수로 구성되는 데이터의 특성을 분석하고 결과가 되는 종속 변수와의 선형적인 상관 관계를 모델링하는 방법이다. 독립 변수와 종속 변수의 상관 관계는 입력 데이터와 출력 결과의 관계로 모델링되어 결과를 예측할 수 있는 기계 학습 방법으로 활용되고 있다. 선형 회귀 모델은 데이터의 통계적인 특성으로부터 결과와의 관계를 수학적인 모델로 표현하는 방법으로 기계 학습 기술이 주목 받기 시작하면서 많은 데이터로부터 통계적인 결과를 예측할 수 있는 모델로 지수 예측 [14], 패턴 인식 [15] 등 응용 분야에서 활용되고 있다.
선형 회귀를 적용할 수 있는 환경은 여러 개의 입력 변수와 상관 관계를 가지고 결과를 예측 가능할 경우 입력 변수에 대한 결과를 모델링하는 회귀 모델을 구성함으로써 가능하다. 독립 변수에 대한 종속 변수의 결과를 예측하기 위해서 회귀 모델의 정확도에 대한 오차를 줄이는 과정을 통해 모델이 최적화되며, 최적화된 선형 회귀 모델을 통해 결과 예측에 적용할 수 있다.
3-2 기본 선형 회귀 모델
선형 회귀 모델은 입력 데이터에 해당하는 독립 변수 x와 데이터로부터 예측하고자 하는 결과에 해당하는 종속 변수 y 사이의 상관 관계로 구성된다. 하나의 독립 변수 x는 입력으로 사용되는 하나 이상 여러 개의 데이터들로 구성되며, 학습을 통해 선형 회귀 모델을 최적화할 수 있도록 많은 수의 데이터 집합을 이용해 학습 모델을 생성한다. 예를 들어, 각 독립 변수 x는 p개의 데이터를 가지고 있고, n개의 학습 데이터를 데이터 집합으로 가진다면, 학습 데이터 집합은 종속 변수 y에 대해서 다음과 같은 수식으로 표현된다.
| (1) |
수식 (1)에서 xi1, ∙∙∙, xip는 독립 변수 x에 포함되는 p개의 데이터를 나타낸다. 그리고, n개의 데이터는 선형 회귀 모델에서 독립 변수 x와 종속 변수 y 사이에 선형 상관 관계를 가지는 모델이 되고, 실제 데이터에 나타나는 오차값 ϵ을 반영하면 선형 모델은 다음과 같은 수식으로 표현된다.
| (2) |
수식 (2)에서 βi는 각 입력 데이터 xi에 대한 상관 계수이며, 선형 회귀 모델에서 독립 변수와 종속 변수 사이의 선형 상관 관계를 결정하는 계수이다. 수식 (2)에서 ϵi는 선형 회귀 모델에서 실제 데이터가 가지는 오차값을 표현하고 있으며, 독립 변수 x와 종속 변수 y 사이의 선형 상관 관계에서 나타나는 데이터의 오차값을 나타낸다. 따라서, 선형 회귀를 이용한 데이터의 기계 학습 과정은 많은 수의 데이터에 대해 이 오차값 ϵi을 최소화할 수 있는 상관 계수 βi를 찾고 선형 회귀 모델을 만드는 것이다.
선형 회귀 분석 모델에서 오차값 ϵ을 최소화하면서 상관 계수 βi를 구하는 방법은 최소 제곱법 (least squares), 최대 가능도 추정 (maximum likelihood estimation) 등을 응용한 형태의 오차 함수를 이용할 수 있으며, 일반적으로 최소 제곱법이 많이 사용된다. 최소 제곱법은 결과 예측을 위한 모델의 분석 과정에서 오차 정도를 표현하기 위해 오차의 제곱을 이용하는 방법이다. 오차 ϵ이 증가함에 따라 오차의 제곱은 가파르게 증가하기 때문에 모델의 오차가 최소화할 수 있도록 선형 회귀 모델을 유지할 수 있다.
이 논문에서 유사 프로그램 분석을 위한 선형 회귀 모델은 최소 제곱법을 이용해서 독립 변수에 대한 종속 변수의 상관 관계를 모델링한다. 학습 데이터의 결과와 선형 회귀 모델에서 예측한 예측값 사이의 오차의 제곱을 최소화하는 상관 계수 β를 찾고, 분석을 위한 선형 회귀 모델을 완성할 수 있다. 오차 ϵi은 다음 수식과 같이 표현된다.
| (3) |
여기서, 는 학습 데이터의 결과를 나타내고, 오차는 이 결과와 수식 (2)의 선형 회귀 모델에서 예측한 결과 yi 사이의 차이로 표현된다. 선형 회귀 모델은 n개의 학습 데이터에 대해서 오차의 제곱의 합을 최소화하는 모델로 학습된다. 여기서, 오차 제곱의 합 SSE (sum of squared errors)는 다음 수식과 같이 표현된다.
| (4) |
따라서, 분석을 위한 선형 회귀 모델은 수식 (4)에서 기술한 학습 데이터와 모델의 예측 결과의 오차 제곱의 합 SSE를 최소로 하는 상관 계수 β를 찾음으로써 완성된다.
3-3 기계 학습 데이터의 슬라이스
선형 회귀에서 입력 데이터가 되는 독립 변수는 여러 개의 특성 데이터로 구성된다. 따라서 학습 데이터는 다차원 데이터로 표현되고, 각 데이터는 입력 데이터의 특성을 표현하는 구성 원소이다. 선형 회귀 모델에서 이런 여러 개의 특성 데이터들이 모여서 하나의 결과를 예측할 수 있는 상관 관계를 구성한다. 반면 전체 특성 데이터 중에서 일부 특성 값들은 실제 올바른 결과를 추정하는데 방해가 되는 노이즈 (noise) 데이터들이 포함될 수 있다. 따라서, 노이즈 특성 값이 결과에 미치는 범위가 커지면 선형 회귀 모델의 오류가 증가할 수 있다. 반면 데이터에 포함된 노이즈 특성 값들의 영향을 효과적으로 제한할 수 있다면 선형 회귀 모델의 정확성을 향상 시킬 수 있을 것이다.
독립 변수에 포함된 특성 데이터 중에서 결과 예측에 방해가 되는 노이즈 데이터를 정확하게 분석하고 제거하기 위해서는 추가적인 데이터 분석이 필요하고, 이를 위해 많은 시간과 노력이 필요하다. 이 논문에서는 학습 데이터에 포함될 수 있는 노이즈 데이터의 오류를 효율적으로 줄이기 위해 선형 회귀 모델의 학습 데이터에 대해 여러 개의 데이터로 분할하는 방법을 제안한다. 기존의 선형 회귀 모델은 학습 데이터 전체를 하나의 선형 회귀 모델로 학습할 수 있도록 설계하지만, 이 논문에서는 분할된 데이터에 대해 여러 개의 선형 회귀 모델을 구성하고, 학습 데이터의 오차에 의한 영향을 분산할 수 있도록 선형 회귀 모델을 설계한다.
데이터 슬라이싱 [16]은 많은 데이터를 가진 환경에서 데이터를 분할해서 추출하는 방법을 의미한다. 슬라이싱은 최적의 데이터 분석을 위해 많은 수의 데이터를 세그먼트로 잘라서 추출하는 방법으로 데이터를 다양한 시각에서 분석할 수 있도록 해준다. 이 논문에서는 데이터의 특성을 분석하기 위해 하나의 데이터를 여러 개의 데이터로 분할하기 위한 방법으로 데이터 슬라이싱을 적용하고 있다.
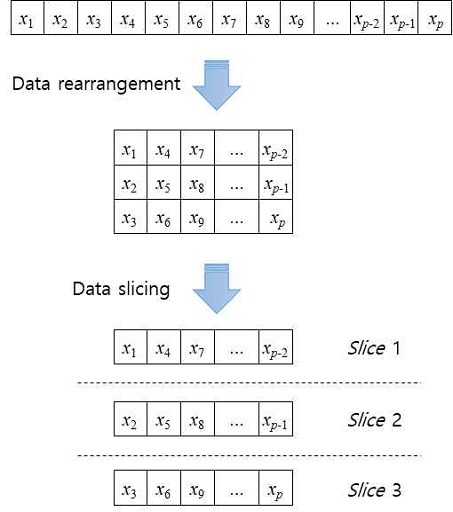
그림 1은 본 논문에서 제안하는 데이터 슬라이싱 과정을 보여주고 있다. 먼저, 학습 데이터를 여러 개의 슬라이스로 분할하기 위해 하나의 데이터에 포함된 p개의 특성 데이터를 순서대로 재배열한다. 데이터의 재배열은 분할하기 위한 데이터 슬라이스의 개수에 따라 데이터의 행이 결정된다. 예를 들어 n개의 데이터 슬라이스로 분할하기 위해서 n개의 행을 가진 공간에 열우선 방식으로 재배열한다. 그림 1은 p개의 특성 데이터에 대해서 3개의 슬라이스로 분할하기 위한 재배열 방법을 보여주고 있다. 재배열된 데이터는 각 행을 따라 분할하고 하나의 학습 데이터는 여러 개의 슬라이스로 분할된다.
데이터의 재배열과 분할을 통해서 얻어진 데이터 슬라이스는 각 데이터의 특성이 선형 회귀 모델의 예측 결과에 영향을 미치는 범위를 해당 슬라이스로 제한하고, 노이즈로 인해 발생하는 분석 모델의 오류를 줄일 수 있다. 데이터를 분할하는 슬라이스는 각각 독립적인 선형 회귀 모델로 학습된다. 따라서 분할되는 데이터 슬라이스의 수가 증가하면 각 슬라이스에 포함되는 데이터의 수는 1/n로 줄어들기 때문에 각 데이터의 상호 의존성을 줄여줄 수 있고, 독립성을 높여줄 수 있다. 반면, 선형 회귀 모델의 증가로 인한 학습의 효율성은 감소한다.
3-4 데이터 슬라이스를 이용한 선형 회귀 모델의 설계
본 절에서는 본 논문에서 제안한 데이터 슬라이스를 이용한 선형 회귀모델을 설계한다. 수식 (1)에서 표현한 독립 변수 x와 종속 변수 y에 대한 n개의 학습 데이터에 대해 그림 1과 같이 데이터 슬라이싱을 적용하면 세 개의 데이터 슬라이스로 분할된다. 따라서, 유사 프로그램의 비교를 위한 학습 데이터를 생성하기 위해서 비교 대상이 되는 두 프로그램 A와 B에 대해 분할된 데이터 슬라이스 sliceA와 sliceB는 다음 수식과 같이 각각 세 개의 데이터 집합으로 표현된다.
| (5) |
두 프로그램의 데이터로부터 유사 프로그램 분석을 위한 학습 데이터를 생성하기 위해 슬라이스의 특성값 차이를 비교한다. 따라서, 두 프로그램의 차이를 비교한 결과는 다음과 같이 모델의 학습을 위한 데이터 슬라이스로 생성된다.
| (6) |
수식 (6)에서 yi는 학습 데이터의 결과값이며, 유사한 프로그램의 비교 데이터인 경우에는 1이 되고 다른 프로그램의 비교 데이터는 0으로 생성한다. 이와 같이 분할된 데이터를 비교한 슬라이스에 대해서 각각 수식 (2), (3), (4)에서 기술한 선형 회귀 모델을 이용하면 세 개의 독립적인 선형 회귀 모델을 만들 수 있다. 각각의 선형 회귀 모델은 입력 데이터에 대한 분류 결과를 예측할 수 있는 독립적인 예측 모델을 구성하고, 이 세 개의 모델을 통합해서 하나의 선형 회귀 모델로 설계한다. 이 때 세 개의 데이터 슬라이스로부터 만들어진 각각의 선형 회귀 모델을 LR1,LR2,LR3이라고 하면 유사 프로그램의 분류를 위한 데이터 슬라이스에 대한 선형 회귀 모델 LRk는 다음 수식과 같이 설계할 수 있다.
| (7) |
여기서 throshold는 유사 프로그램의 분류 기준을 결정하는 임계값을 나타낸다. 모델의 분석과 실험을 통해 양성과 음성을 구분하는 최적의 임계값을 정할 필요가 있으며, 이 논문에서는 양성과 음성을 구분하는 1과 0의 중간값 50%를 임계값으로 사용한다. 따라서, 임계값 50%를 넘어서는 값이 나오면 분석 결과를 1로 예측하고 유사 프로그램으로 분류하는 선형 회귀 모델을 설계할 수 있다.
데이터 슬라이스로부터 설계된 각각의 선형 회귀 모델을 통합하면 전체 데이터에 대한 선형 회귀 모델을 설계할 수 있다. 데이터 슬라이싱을 통해 나눠진 데이터를 통합하는 선형 회귀 모델 LRSum은 다음 수식과 같이 설계된다.
| (8) |
수식 (8)은 데이터 슬라이싱 방법을 통해서 여러 개의 슬라이스로 나눠진 각각의 선형 회귀 모델을 하나로 통합하는 모델을 나타내고 있다. 데이터 슬라이스의 통합 선형 회귀 모델로부터 유사 프로그램을 분류할 수 있는 분류 모델 LRDS은 다음과 같이 설계된다.
| (9) |
수식 (9)는 데이터 슬라이싱을 통해 구성된 각 선형 회귀 모델을 통합한 후 유사 프로그램의 최종 분류 결과를 예측하기 위해 임계값 threshold 보다 큰 예측 결과에 대해서 유사 프로그램으로 분류할 수 있는 통합된 선형 회귀 분석 모델을 나타내고 있다.
Ⅳ. 데이터 슬라이스를 이용한 모델의 실험
4-1 실험 환경의 구성 및 유사 프로그램 분석 모델의 구현
본 절에서는 이 논문에서 제안한 선형 회귀에 대한 데이터 슬라이싱 접근 방법을 구현하고 기존의 일반적인 선형 회귀 방법과 비교 실험을 수행한다. 본 실험을 위해 3장에서 기술한 데이터 슬라이싱과 선형 회귀 모델을 이용한 유사 프로그램 분류 모델을 구현하였다. 본 논문에서 제안한 방법과 기존의 선형 회귀 모델 [17]의 예측 결과의 정확성을 비교하기 위해서 동일한 환경에서 실험을 수행하였다. 표 1은 분석 결과의 비교 실험을 수행하기 위해 구성된 실험 환경을 보여주고 있다.
본 논문에서 제안한 데이터 슬라이싱과 이를 적용한 선형 회귀 모델의 실험은 Microsoft Windows 7 운영 체제에서 수행되었고, 기계 학습에서 널리 사용되고 있는 프로그래밍 언어인 Python을 이용해서 분석 모델을 구현하였다. 비교 실험을 위해 사용한 벤치마크 데이터의 형식은 자바 프로그램으로부터 생성되는 자바 클래스 파일 형식을 이용하였으며, 데이터 슬라이스 분석기는 자바 클래스파일 형식의 데이터로 부터 자바 바이트 코드 구성 정보를 분석하고 학습 데이터를 위한 슬라이스를 생성한다. 데이터 슬라이스에 대한 선형 회귀 분석과 분류 모델을 구현하기 위해서 Python과 함께 scikit-learn [18]을 이용하였다.
선형 회귀 분석을 위한 학습 데이터로 자바 클래스파일에 포함된 바이트코드의 분포 정보를 분석하고 프로그램에 포함된 빈도를 반영한 학습 데이터를 생성하였다. 학습 결과를 반영하는 종속 변수 y는 유사 프로그램을 분류할 수 있는 모델을 반영하기 위해 수식 (6)과 수식 (8)에서 설계한 방법으로 유사 프로그램 사이의 학습 데이터는 y = 1 로 학습하고, 서로 다른 프로그램의 학습 데이터는 y = 0 으로 학습하도록 구현하였다. 비교 실험을 위한 소프트웨어 데이터의 전처리를 위해 데이터를 분할하고 데이터 슬라이스 셋을 생성하는 데이터 슬라이스 분석기 (data slicer)를 구현하고, 이를 이용해서 원본 소프트웨어 데이터에 대한 슬라이스를 생성하였다. 생성된 각 데이터 슬라이스는 특성값의 비교를 통해서 두 슬라이스의 차이를 특성값으로 가지는 선형 회귀 모델의 학습 데이터로 이용할 수 있다.
4-2 학습을 통한 선형 회귀 모델의 생성
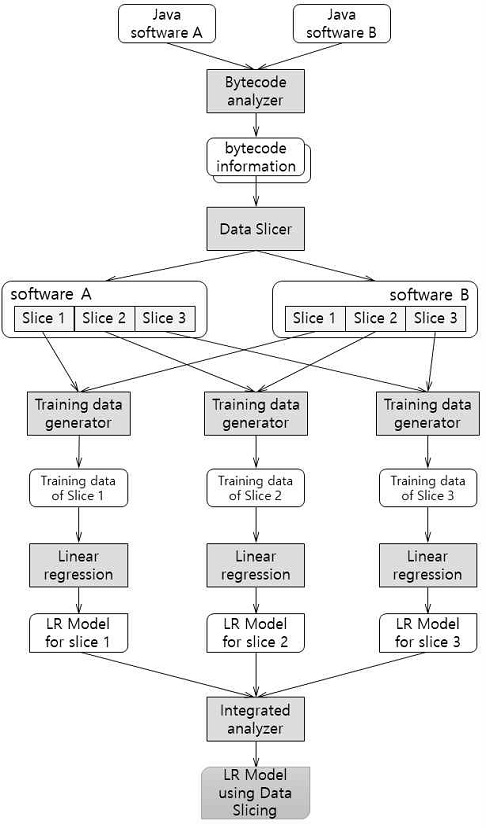
본 논문에서 제안한 데이터 슬라이싱을 적용한 선형 회귀 모델은 그림 2와 같은 구조로 구성된다. 자바 바이트코드 분석기는 학습 데이터로 사용되는 자바 소프트웨어로 부터 소프트웨어의 특성을 나타내는 바이트코드 정보를 생성한다. 분석된 하나의 바이트코드 정보는 데이터 슬라이스 분석기(data slicer)를 통해서 여러 개의 데이터로 분할되고 데이터 슬라이스를 생성한다. 선형 회귀 모델의 학습 데이터를 생성하기 위해서 학습 데이터 생성기(training data generator)는 두 프로그램의 슬라이스를 비교하고 결과를 학습 데이터로 생성한다. 데이터 슬라이스의 비교를 통해 생성된 학습 데이터는 선형 회귀 분석을 통해서 학습되고, 각 슬라이스에 대한 유사 프로그램 분석을 위한 선형 회귀 모델이 생성된다. 각각의 분석 모델은 하나의 분석 모델로 통합되고, 통합 분석기(integrated analyzer)의 결과를 통해 유사 프로그램을 분석할 수 있다.
이 실험은 학습 데이터에 대해 데이터 슬라이싱을 적용한 선형 회귀 모델을 완성하는 학습 과정과 학습을 통해 생성된 유사 프로그램 분류 모델의 평가를 위한 테스트 과정으로 구성된다. 다음의 표 2는 선형 회귀 모델의 학습을 수행하기 위해 이 실험에서 사용한 학습 데이터의 정보를 보여주고 있다.
본 실험 환경에서 성능 평가를 위해 사용한 데이터는 자바 프로그램의 실행 파일 형식인 자바 클래스 파일을 대상으로 하고 있다. 분석 모델을 생성하기 위한 학습 과정을 위해 학습 데이터로 Jakarta-ORO [19]를 이용하였다. Jakarta-ORO는 자바 프로그램에서 정규식을 지원하기 위한 텍스트 처리 자바 클래스들을 포함하고 있는 프로그램이다. 본 학습에 사용한 소프트웨어는 50개의 클래스파일로 구성되어 있고, 프로그램으로부터 추출한 특성 데이터는 최대 923개, 평균 144개의 바이트코드를 포함하고 있다. 비교 결과의 신뢰성을 위해서 바이트코드의 수가 50개 이상인 클래스파일 26개를 대상으로 실험을 수행하였다.
유사 프로그램의 분석을 위한 학습 데이터를 생성하기 위해서 자바 프로그램의 구조를 변경하고 유사한 프로그램을 생성할 수 있는 Smokescreen 자바 난독화 소프트웨어 [20]을 사용하였다. Smokescreen 소프트웨어는 프로그램에 사용된 이름을 변경하고, 프로그램이 실행하는 제어 흐름 구조와 실행 명령어의 패턴을 변경하기 때문에 프로그램을 이해하기 어렵게 난독화하고, 원본 프로그램을 동일한 결과를 수행하는 유사 프로그램으로 변경할 수 있다. Smokescreen의 변환 옵션을 통해 변경된 자바 프로그램 버전들은 유사 프로그램 비교를 위한 학습 데이터를 생성하기 위해 사용하였다. 프로그램의 원본과 Smokescreen을 이용해 변경된 버전은 각각 교차 비교를 통해 학습 데이터 슬라이스를 생성하고, 동일 버전의 비교 데이터는 유사 프로그램을 위한 학습 데이터로 사용하고, 상이한 프로그램의 비교 데이터는 다른 프로그램의 학습 데이터로 사용하였다. 다른 프로그램의 비교 데이터에 비해 유사 프로그램 비교 데이터가 부족하기 때문에 유사 프로그램의 비교 데이터는 오버샘플링을 하였다. 또한, 기존의 선형 회귀 모델과 비교 실험을 수행하기 위해서 동일한 실험 환경에서 각각 선형 회귀 모델을 생성하였다.
4-3 실험 결과
본 논문에서 제안한 데이터 슬라이싱을 이용한 선형 회귀 모델의 정확성을 평가하기 위해 기존의 일반 선형 회귀 모델의 분석 결과와 비교하는 실험을 수행하였다. 두 모델의 비교 실험을 수행하기 위해 동일한 테스트 데이터를 이용해서 분석 정확도를 비교하였다. 표 3은 비교 실험에서 사용한 테스트 데이터의 정보를 보여주고 있다. 이 실험에서 분석 결과를 비교하기 위한 테스트 데이터로 ANTLR(ANother Tool for Language Recognition)을 사용하였다. ANTLR [21]은 텍스트나 파일을 읽고 구문 분석을 수행하는 파서 제너레이터 (parser generator) 프로그램이다. 테스트 데이터로 사용된 자바 클래스 파일은 총 117개이고, 테스트 데이터는 최대 1,646개의 바이트코드를 포함하고 있으며, 평균 바이트코드의 개수는 172개이다. 바이트코드의 수가 50개 이상인 64개의 클래스파일을 대상으로 4-2절의 선형 회귀 모델을 학습하기 위한 데이터와 동일한 방법으로 총 7,424개의 테스트 데이터를 생성하였다.
표 4는 두 모델의 정확도 비교 실험 결과를 보여주고 있다. 표에서는 두 분석 방법에서 동일한 학습 데이터에 대해 생성된 분석 모델에 대한 테스트 데이터의 분석 결과를 비교하고 있다. 전체 테스트 데이터의 수는 7,424개이며, 유사 프로그램에 대한 테스트 데이터 3,136개이고, 서로 다른 프로그램에 대한 테스트 데이터 4,288개이다. 유사 프로그램의 예측 분석 결과에서 기존의 선형 회귀 모델을 적용한 경우에는 6,514개의 테스트 데이터에 대해 올바른 결과를 예측하였고, 665개의 위양성(false positive)과 245개의 위음성(false negative) 결과가 나왔다. 전체 분석 정확도는 87.7%를 보여주었다. 본 논문에서 제안한 데이터 슬라이싱을 적용한 분석 모델에서는 7,107개의 테스트 데이터에 대해서 정확한 예측 결과를 보여주었으며, 317개의 위양성 결과가 나오면서 분석 정확도는 95.7%를 보여주었다. 위음성 결과는 나타나지 않았으며 위양성 결과도 기존의 방법과 비교할 때 줄어드는 것을 확인할 수 있었다.
비교 실험 결과에서 데이터 슬라이스를 이용한 선형 회귀 분석 모델은 기존의 일반적인 선형 회귀 방법과 비교할 때, 약 8% 정도 정확도가 향상하였으며, 위양성과 위음성의 수도 줄어드는 것을 확인할 수 있었다. 기존의 선형 회귀 모델은 각 학습 데이터에 대해 하나의 단독 선형 회귀 모델을 생성한다. 기존의 방법은 하나의 모델만 생성하기 때문에 학습 데이터에서 예측 결과에 오류를 발생할 수 있는 노이즈 값이 포함되어 있을 때, 노이즈 특성에 의해 전체 결과에 영향을 미칠 수 있다. 반면, 본 논문에서 제안한 방법은 학습 데이터의 특성들을 여러 개의 학습 데이터로 분할함으로써 결과에 오류가 나타날 수 있는 데이터의 영향 범위를 분할된 범위내로 제한하는 효과를 얻을 수 있다. 분산된 데이터의 선형 회귀 모델을 통합하는 과정을 통해 학습 데이터의 오류로 인한 학습의 영향을 줄일 수 있다고 평가된다.
실험 결과에서 이 논문에서 제안한 데이터 슬라이싱을 이용한 선형 회귀 모델은 학습 데이터에 포함된 데이터의 특성을 분할하고, 오류를 발생하는 노이즈의 영향을 국소화함으로써 전체 예측 결과의 정확성을 향상시킬 수 있었다. 본 논문에서 제안한 방법은 선형 회귀 모델에서 데이터의 학습 방법을 개선하고, 선형 회귀를 이용한 예측 모델을 설계할 때 예측 오류를 줄이기 위한 방법으로 적용될 수 있을 것이다.
Ⅴ. 결 론
오늘날 정보 시스템을 이용한 서비스에서 소프트웨어의 역할은 지속적으로 증가하고 있다. 소프트웨어의 중요성이 증가함에 따라 소프트웨어 개발의 생산성과 안전성을 확보하기 위한 소프트웨어 분석 기술과 소프트웨어의 특성을 이해하기 위한 노력이 필요하다. 이 논문에서는 소프트웨어의 특성 정보 분석을 통한 유사 소프트웨어를 분석하기 위해 선형 회귀 모델을 이용하고, 기계 학습 방법의 정확성을 향상시키기 위한 데이터 슬라이싱 방법을 제안하고 있다.
기계 학습은 학습 데이터를 이용한 학습 과정을 통해 문제를 해결할 수 있는 모델을 생성하고 결과를 예측하는 접근 방법이다. 기계 학습 모델을 생성하기 위해서 사용하는 학습 데이터의 정확도는 분석 결과의 정확도에 중요한 역할을 한다. 이 논문에서는 선형 회귀 분석 모델의 학습 정확도를 개선하기 위해서 학습 데이터를 분할하는 슬라이싱을 적용하는 기법을 제안하였다. 학습 데이터의 슬라이스를 이용해 유사 프로그램을 분석할 수 있는 선형 회귀 모델을 설계하고 실험을 수행하였다. 실험 결과에서 데이터 슬라이싱을 통한 선형 회귀 모델은 기존의 선형 회귀 모델과 비교할 때 분석 정확도가 개선되는 것을 확인할 수 있었다. 본 논문에서 제안한 데이터 슬라이싱 방법은 선형 회귀 모델을 이용한 예측 모델에서 학습 데이터를 효율적으로 처리하고 모델의 정확도를 개선하기 위해 적용될 수 있을 것이라 기대된다.
Acknowledgments
이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임 (No. NRF-2017R1D1A1B 03034769).
참고문헌
-
Heewan Park, Hyun-il Lim, Seokwoo Choi, and Taisook Han, “Detecting Common Modules in Java Packages Based on Static Object Trace Birthmark,” in The Computer Journal, Vol. 54, No. 1, pp. 108-124, Jan. 2011.
[https://doi.org/10.1093/comjnl/bxp095]

-
Ginger Myles and Christian Collberg, “Detecting software theft via whole program path birthmarks,” in International Conference on Information Security (ISC 2004), LNCS 3225, pp. 404-415, 2004.
[https://doi.org/10.1007/978-3-540-30144-8_34]

-
Haruaki Tamada, Masahide Nakamura, Akito Monden, Ken-ichi Matsumoto, “Java Birthmarks - Detecting the Software Theft,” in IEICE Transactions on Information and Systems. Vol. 88-D, No. 9, Sept. 2005.
[https://doi.org/10.1093/ietisy/e88-d.9.2148]

- Mamoun Alazab, Robert Layton, Sitalakshmi Venkatraman, and Paul Watters, “Malware Detection Based on Structural and Behavioural Features of API Calls,” in International Cyber Resilience conference, Mar. 2012.
-
Michael J. Wise, “Yap3: Improved detection of similarities in computer program and other texts,” In Proceedings of the 27th SIGCSE Technical Symposium on Computer Science Education, pp. 130-134, 1996.
[https://doi.org/10.1145/236462.236525]

-
Ginger Myles and Christian Collberg, “k-gram based software birthmarks,” in Proceedings of the 2005 ACM Symposium on Applied Computing, pp. 314-318, 2005.
[https://doi.org/10.1145/1066677.1066753]

- Krinke J, “Identifying similar code with program dependence graphs,” in Working Conference on Reverse Engineering 2001, pp. 301-309, 2001.
-
M. White, M. Tufano, C. Vendome and D. Poshyvanyk, “Deep learning code fragments for code clone detection,” 31st IEEE/ACM International Conference on Automated Software Engineering (ASE), pp. 87-98, Singapore, 2016.
[https://doi.org/10.1145/2970276.2970326]

- Daniel Heres, “Source Code Plagiarism Detection using Machine Learning,” Master Thesis, Utrecht University, August 2017.
-
Upul Bandara and Gamini Wijayarathna, “A Machine Learning Based Tool for Source Code Plagiarism Detection,” International Journal of Machine Learning and Computing, Vol. 1, No. 4, pp. 337-343, October 2011.
[https://doi.org/10.7763/IJMLC.2011.V1.50]

-
Niccolo Marastoni, Roberto Giacobazzi, and Mila Dalla Preda, “A deep learning approach to program similarity,” MASES 2018: in Proceedings of the 1st International Workshop on Machine Learning and Software Engineering in Symbiosis, pp. 26-35, September 2018.
[https://doi.org/10.1145/3243127.3243131]

-
Noam Shalev and Nimrod Partush, “Binary Similarity Detection Using Machine Learning,” PLAS '18: in Proceedings of the 13th Workshop on Programming Languages and Analysis for Security, pp. 42-47, January 2018.
[https://doi.org/10.1145/3264820.3264821]

-
Hyun-il Lim, “Design of Similar Software Classification Model through Support Vector Machine,” Journal of Digital Contents Society, Vol. 21, No. 3, pp. 569-577, Mar. 2020.
[https://doi.org/10.9728/dcs.2020.21.3.569]

-
Dinesh Bhuriya, Girish Kaushal, Ashish Sharma, and Upendra Singh, “Stock market predication using a linear regression,” in 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, pp. 510-513, Apr. 2017.
[https://doi.org/10.1109/ICECA.2017.8212716]

-
Priya Stephen and Suresh Jaganathan, “Linear regression for pattern recognition,” in 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), pp. 1-6, Mar. 2014.
[https://doi.org/10.1109/ICGCCEE.2014.6921393]

- Jiawei Han, Micheline Kamber, and Jian Pei, Data Mining Concepts and Techniques, Third Edition, Morgan Kaufmann Publishers, 2012.
-
Hyun-il Lim, “Similarity Analysis of Programs through Linear Regression of Code Distribution,” Journal of Digital Contents Society, Vol. 19, No. 7, pp. 1357-1363, July 2018.
[https://doi.org/10.9728/dcs.2018.19.7.1357]

- scikit-learn: Machine Learning in Python [Internet]. Available: http://scikit-learn.org/stable/, .
- The Jakarta-ORO [Internet]. Available: https://jakarta.apache.org/oro/, .
- Smokescreen – Java obfuscator, http://www.javadevelopmentindia.com/technology-amp-integration/technology-amp-integration/obfustication-amp-decompiling/smokescreen/, .
- ANTLR (ANother Tool for Language Recognition) [Internet]. Available: http://www.antlr.org/
저자소개

1995년 : KAIST 전산학과 (공학사)
1997년 : KAIST 전산학과 (공학석사)
2009년 : KAIST 전산학과 (공학박사)
2009년~2010년: KAIST 전산학과 연구원
2010년~현 재: 경남대학교 컴퓨터공학부 부교수
※관심분야:소프트웨어 분석, 소프트웨어 보안, 인공 지능, 기계 학습, 소프트웨어 공학, 프로그래밍 언어 등