유틸리티-리스트를 이용한 높은 유틸리티 항목집합 마이닝
Copyright ⓒ 2020 The Digital Contents Society
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-CommercialLicense(http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록
높은 유틸리티 항목집합 마이닝(High Utility Itemset Mining)은 트랜잭션에서 각 항목의 가중치(item profit)와 항목의 발생빈도를 함께 고려하여 사용자가 지정한 임계값 이상의 유효한 항목집합을 추출한다. 유틸리티 항목집합 마이닝은 항목의 조인 연산을 통해 새로운 항목집합을 생성하면서 임계값을 만족하는지 여부를 판단하기 때문에 높은 조인 연산 비용이 요구된다. 이 논문에서는 유틸리티-리스트 구조를 이용하고, 항목의 조인에 따른 연산 비용을 줄이기 위해 유틸리티-리스트 구조에 prefix 항목의 유틸리티를 포함한다. 그리고 높은 유틸리티 항목집합이 될 가능성을 검사하기 위해 비트연산을 이용하는 알고리즘을 제안한다. 실험결과를 통해 제안하는 알고리즘이 기존의 알고리즘에 비해 최대 2.4배 성능 향상이 있음을 보여주었다.
Abstract
High utility itemset mining extracts valid itemsets above a user-specified threshold by taking into account the profit of each item and the frequency of items occurring in the transaction. The utility itemset mining requires a high cost of join operation because it determines whether a threshold is met while creating a new itemset through the join of items. In this paper, the utility-list structure includes the prefix item utility to reduce the computational cost of joining items, and our algorithm uses bit operation to check the possibility of becoming a high utility itemset. Experimental results showed that the proposed algorithm was up to 2.4 times better performance than the existing algorithm in the execution time.
Keywords:
Data Mining, Utility Mining, High Utility Itemset, Frequent Pattern, Pattern Mining키워드:
데이터 마이닝, 유틸리티 마이닝, 높은 유틸리티 항목집합, 빈발 패턴, 패턴 마이닝Ⅰ. 서 론
데이터 마이닝은 대용량 데이터베이스로부터 유용하고 중요한 패턴이나 정보를 추출하는 기법이다[1-5]. 최근 무선 센서 네트워크, 사물 인터넷, 소셜 네트워크 서비스와 같은 다양한 응용 분야에서 대용량의 데이터가 생성됨에 따라 이를 효율적으로 분석하여 유용한 정보를 찾아내기 위한 데이터 마이닝 기술의 중요성이 더욱 높아지고 있다[5-7].
항목집합 마이닝은 데이터 마이닝 기법 중 연관규칙 탐사에서 항목들간의 상관관계를 찾는 탐사 기술을 의미한다. 빈발 항목집합 마이닝(Frequent Itemset Mining)[3,4]은 데이터베이스로부터 항목의 빈도를 기반으로 미리 정의된 임계치를 만족하는 유효 항목집합을 추출한다. 이러한 빈발 항목집합 마이닝은 각 항목을 같은 중요도로 가정하여 빈발 항목을 추출하므로 항목의 실제 가치나 이윤을 반영하기 어렵다.
높은 유틸리티 항목집합 마이닝(High-Utility Itemset Mining, HUIM)은 데이터 항목(item)에 대해 다른 가중치(profit)를 고려할 수 있는 장점으로 인해 비즈니스 데이터 분석 환경에서 효율적으로 이용될 수 있다[8-10]. 예를 들어 서로 다른 가격의 제품들을 다른 중요도를 갖는 유틸리티 데이터 집합으로 간주할 수 있고, 이것은 실생활에서 쉽게 적용될 수 장바구니 분석에 적용될 수 있다. 장바구니 분석에서 빈번하게 발생하는 항목이지만 수익률은 낮은 생필품 같은 제품들이 있고, 자주 발생하지 않지만 수익률이 높은 보석류의 제품들이 있다. 그러므로 비즈니스 분야에서 수익을 고려한 마케팅 등과 관련된 중요한 결정을 할 수 있고, 수익에 큰 기여를 하는 제품과 더불어 해당 제품과 관련된 고객의 정보를 발견할 수도 있다. 이외에도 유전자의 중요도를 고려해야 하는 생물학적 유전자 데이터베이스와 웹 페이지의 중요도가 다른 웹 클릭 스트림 분석 등에도 적용할 수도 있다[11,12].
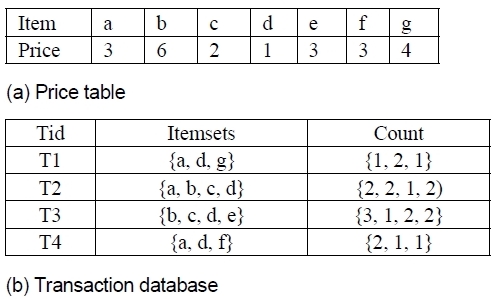
대부분의 빈발 항목집합 마이닝 알고리즘에서는 안티모노톤 특성(Anti-monotone property)을 이용하였다. 즉, 빈발하지 않은 항목집합은 그 항목집합을 포함하는 수퍼셋(supersets)은 빈발하지 않다. 그러므로 빈발하지 않은 항목집합이 식별되면 그 항목집합의 수퍼셋에 대한 빈발여부를 검사를 하지 않고 가지치기 하여 마이닝의 수행 성능을 높일 수 있었다. 그러나 높은 유틸리티 마이닝에서는 안티모노톤 특성을 적용할 수 없다. 그림 1의 데이터베이스를 예를 들어 설명하면 각 항목은 값(price)이 있고, 하나의 트랜잭션에서 발생하는 항목의 빈도가 있다. 높은 유틸리티 항목집합 마이닝에서는 항목의 발생빈도와 값을 고려하여 미리 정의된 임계치를 만족하는 항목집합을 높은 유틸리티 항목집합이라고 한다.
예를 들어, 항목집합 {a}, {ab}, {abc}, {abcd}의 지지도는 3, 1, 1, 1이지만 이들의 유틸리티는 15, 18, 20, 22이다. 임계치를 20으로 가정하면 항목집합 {abc}는 높은 유틸리티 항목집합이 되고, 이는 낮은 유틸리티(low utility) 항목집합 {a}, {ab}를 포함하고 있다. 그러므로 높은 유틸리티 항목집합 마이닝에서는 빈발 항목집합 마이닝에서 적용했던 안티모노톤의 특성을 적용하여 가지치기 할 수 없다.
이 논문에서는 높은 유틸리티 항목집합 마이닝의 성능을 개선하기 위하여 최근에 제안된 유틸리티-리스트 구조에 항목의 조인에 따른 유틸리티 계산시간을 줄이기 위한 prefix 항목의 유틸리티 값을 저장한다. 그리고 높은 계산비용이 요구되는 조합 가능한 항목집합의 유틸리티-리스트 구조를 만들기 이전에 항목집합의 조인으로 후보 항목집합이 될 수 있는 가능성을 검사하기 위하여 이들 항목집합을 공통으로 포함하는 트랜잭션의 존재여부를 미리 검사한다. 그리고 후모항목집합이 될 가능성이 있는 항목집합에 대해서만 조인된 새로운 항목집합의 유틸리티-리스트 구조를 생성하는 방법을 제안한다.
본 논문의 구성은 다음과 같다. 2장에서는 관련연구를 기술하고 3장에서는 우리가 제안하는 마이닝 알고리즘을 설명한다. 그리고 4장에서는 실험을 통해 제안한 방법의 성능에 대해 기술하고 5장에서 결론으로 맺는다.
Ⅱ. 관련연구
2-1 빈발 항목집합 마이닝
사용자가 지정한 최소 지지도로 빈발한 항목집합들을 찾아내는 빈발 항목집합 마이닝은 높은 유틸리티 항목집합 마이닝이 등장하기 이전에 항목의 존재 유무만으로 마이닝하는 기법이다. 빈발 항목집합 마이닝의 대표적인 알고리즘인 Apriori[1]는 Breath First Search (BFS) 방식을 사용하고, FP-Growth[2]는 Depth First Search(DFS) 방식을 이용한다. Apriori 기반의 접근 방법은 많은 후보 패턴을 생성하고 여러 번 데이터베이스를 스캔해야 하는 단점이 있다. 이러한 단점을 개선하기 위해 FP-Growth는 트리 분할 방식을 이용하여 conditional FP-tree를 만드는 방식으로, 두 번의 데이터베이스 스캔을 통해 후보 생성 없이 빈발 항목집합들을 식별한다. 이러한 알고리즘은 후보 항목집합의 수를 줄이기 위해 안티 모노톤 특성을 사용하였다. 그리고 빈발 항목집합 마이닝에 대한 연구는 항목의 중요도를 다르게 고려하여 높은 가중치 항목집합을 발견하는 가중치 빈발 항목집합 마이닝(Weighted FIM)[6,7]으로 발전하였고, 항목의 수량과 중요도를 함께 고려하는 높은 유틸리티 항목집합 마이닝으로 진행되었다.
2-2 높은 유틸리티 항목집합 마이닝
항목의 수량과 항목의 가중치를 동시에 고려하는 유틸리티 마이닝의 기존 알고리즘[10, 11]은 후보항목 생성을 포함하는 두 단계로 구성된다. 첫 번째 단계에서 high utility patterns이 될 가능성 있는 후보패턴을 찾고, 두 번째 단계에는 후보패턴으로부터 high utility patterns을 식별하기 위해 한 번이상의 raw data를 스캔하는 과정을 거친다. 후보 항목을 생성할 때는 주어진 패턴의 슈퍼 패턴들이 가질 수 있는 estimated utility를 적용하고, 두 번째 단계에서는 후보 패턴들의 실제 유틸리티를 계산하여 하이 유틸리티 패턴을 식별한다. 이 알고리즘은 실제 유틸리티 값 대신에 추정된 값을 사용하기 때문에 데이터베이스를 재스캔해야 하고 후보 항목집합들의 실제 유틸리티 값을 다시 계산하는 비용이 발생한다. 그리고 유틸리티 최대값을 이용하여 가지치기 하는 UMining과 경험적인 접근법을 기반으로 가지치기 하는 UMining_H이 제안되었다[12]. 그러나 후보항목 생성 과정에서 불필요하게 많은 패턴들을 생성하는 문제점이 있다. UP-Growth+알고리즘[13]에서는 Transaction Weighted Utility(TWU) 개념을 이용하여 Apriori 속성을 적용하였다. 그러나 실제 유틸리티 값을 사용하지 않고 과대평가된 값을 이용하기 때문에 불필요한 후보 항목집합이 생성된다. 트리구조를 사용하는 연구[14-16]도 있지만 [17]은 검색 범위를 줄이기 위한 방법으로 transaction-id, item-utility, remaining utility로 구성된 리스트 구조를 이용하였다. 각 항목에 대한 리스트 정보를 이용하고, 항목간의 조인을 통해 패턴을 확장하는 방법으로, 실제 유틸리티 값을 이용하기 때문에 estimated utility를 사용하는 방법과 비교하면 후보 항목을 줄이는 효과가 있다. 또한 HUI-Miner 알고리즘[17]을 확장한 FHM 알고리즘[18]이 제안되었다. 유망하지 않은 후보항목의 생성을 미리 제거하기 위하여 2-item에 대한 TWU를 매트릭스로 구성하고, 임계치를 만족하지 않는 2-item은 해당항목의 수퍼셋도 유망하지 않다고 판단하여 조인 연산을 하지 않는 방법으로 성능을 향상시켰다.
Ⅲ. 유틸리티-리스트 기반 높은 유틸리티 항목집합 마이닝
이 장에서는 유틸리티 항목집합 마이닝을 하기 위한 기본 개념을 정의하고, 이 논문에서 제안하는 높은 유틸리티 항목집합의 마이닝 방법을 설명한다.
데이터베이스 D는 트랜잭션들 T={t1, t2,.., tn}으로 구성되고, 각 트랜잭션에는 항목들을 포함한다. 항목들의 집합 I={i1, i2,.., im}에서 트랜잭션에 포함된 각 항목 ij는 수량 q(ij)과 단위 가격 p(ij)으로 구성된다. 유틸리티 마이닝을 설명하기 위해 그림 1의 예제 데이터베이스를 이용한다. 하나의 트랜잭션 Tp에 포함된 항목 ir의 유틸리티(utility), u(ij, Tp) = p(ij) × q(ij, Tp) 이다. 예를 들면 항목 a의 유틸리티 u(a, T1) = 3 × 1 = 3 이고, 항목집합 ad의 유틸리티 u(ad, T1) = u(a, T1) + u(b, T1)=3 + 2 =5이다. 각 항목의 조인으로 생성된 항목집합의 항목 개수를 항목의 길이(length)라고 하고 항목집합 ad는 2-item으로 표현한다. 이러한 기본 개념과 표기를 기반으로 다음을 정의한다.
정의 1. (Itemset Utiltiy) 항목집합 X의 유틸리티는 u(X)로 표현하고, 정의는 다음과 같다.
| (1) |
여기서 u(X, Tp) 는 트랜잭션 Tp에서의 항목집합 X의 유틸리티이다.
정의 2. (High Utility Itemset) 항목집합이 사용자가 정의한 최소 유틸리티 임계치 min_util를 만족하면 높은 유틸리티 항목집합이라고 정의한다. 즉, u(X) ≥ min_util 이면 항목집합 X는 높은 유틸리티 항목집합이다.
정의 3. (Transaction Utility) 트랜잭션 Tp의 트랜잭션 유틸리티(Transaction utility)는 TU(Tp)로 표현하고, 정의는 다음과 같다.
| (2) |
예를 들면, TU(T4) = u(a, T4) +u(d, T4) + u(f, T4) = 6+1+3=10이다. 표 1은 각 트랜잭션의 유틸리티를 나타내고, 데이터베이스 유틸리티의 총합은 69이다.
정의 4. (Transaction Weight Utility) 트랜잭션 가중치 유틸리티(transaction weighted utility)는 항목집합 X를 포함하는 모든 트랜잭션 유틸리티의 합이고, TWU(X)로 표현하며 정의는 다음과 같다.
| (3) |
예를 들면, TWU(ad)=TU(T1)+TU(T4)=9+10=19이다.
정의 5. (Remaining Utility) 트랜잭션 TP에서 항목집합 X 이후의 나타나는 항목집합을 X/r 이라 표기하고, X의 remaining utility, ru(X, Tp)의 정의는 다음과 같다.
| (4) |
예를 들어, ru(ab, T2)=u(cd, T2)=4이다.
이 논문에서 제안하는 마이닝 방법에서는 높은 유틸리티 항목집합을 탐사하는 계산비용과 항목들의 조인연산 비용을 줄이기 위해, 유틸리티-리스트 구조를 이용하고 항목의 존재여부를 비트로 표현하여 비트 AND 연산을 통해 조인 가능성이 있는 항목들만 조인 연산을 수행한다.
마이닝을 하기 위한 모든 항목집합의 유틸리티 정보를 저장하기 위한 유틸리티-리스트 구조에 대한 정의는 다음과 같다.
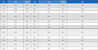
정의 6. (Prefix Utility) 유틸리티-리스트 구조의 한 속성인 prefix utility는 pu(X)로 표현하고, 한 트랜잭션에서 k-item의 prefix utility는 (k-1)-item의 유틸리티이다. prefix utility는 항목집합의 조인 연산에서 유틸리티 계산비용을 줄이기 위해 저장한다. 1-item은 prefix 항목이 없으므로 0으로 초기화된다. 예를 들면 pu(a, T2)=0이고, pu(ab, T2)=u(a, T2)=6이다.
정의 7. (Utility-List) 유틸리티-리스트는 각 항목집합의 유틸리티를 저장하기 위한 구조이고, 트랜잭션 번호(TID), 유틸리티(u), 나머지 유틸리티(ru), prefix 유틸리티(pu)로 구성된다. 항목집합 X를 포함하는 tid, 그리고 트랜잭션에서 해당 항목집합의 유틸리티인 u(X, Tp)와 한 트랜잭션에서 해당 항목집합 이후의 나머지 항목들 X/r의 유틸리티 를 계산하여 ru에 저장한다.
높은 유틸리티 항목집합을 마이닝 하는 과정은 다음과 같다.
먼저 데이터베이스 스캔을 통해 모든 항목에 대한 TWU(X)를 계산하여 미리 주어진 min_util를 만족하지 못하는 항목들은 마이닝 대상에서 제외된다. 그리고 두 번째 과정은 스캔을 통해 min_util를 만족하는 항목들에 대한 TWU(X)를 기준으로 오름차순 정렬하여 트랜잭션을 재구성하고, 모든 1-item 항목의 유틸리티-리스트 구조를 생성한다. 표 2는 각 항목의 트랜잭션 가중치 유틸리티를 보여준다.
모든 트랜잭션 유틸리티의 합은 TU(D)=∑TU(Tj), Tj∈D 이고, 이것은 데이터베이스의 유틸리티를 의미한다. high utility item이 되는 최소 임계치, min_util은 전체 트랜잭션의 TWU에 대해 사용자로부터 주어진 minimum utility threshold, δ을 적용하여 min_util = TU(D)×δ 으로 정의한다. 임의의 항목집합 X가 u(X)≥ min_util 이면 항목집합 X는 높은 유틸리티 항목집합에 속한다. 마이닝 알고리즘을 설명하기 위해 δ=0.3 가정하고, 이를 그림 1에 적용하면 min_util=69*0.3=20.7이다.
데이터베이스 스캔을 통해 그림 1의 모든 항목에 대해 TWU(X)를 계산하여, min_util를 만족하지 않는 항목 f, g은 가지치기하고, TWU(X)에 따라 오름차순 정렬하면 TWU(e)=28 < TWU(a)=41 < TWU(c)=50 < TWU(b)=50 < TWU(d)=69 이다. 이들 항목에 대해 트랜잭션을 재구성한 것이 표 3이다.
유틸리티 리스트 구조는 네 개의 속성 tid, u, ru, pu로 구성된다. 항목집합 X를 포함하는 트랜잭션 식별자 tid, utility value를 표현하는 u(X), 해당 트랜잭션에서 항목집합 이후에 존재하는 항목들의 유틸리티를 나타내는 ru(X), 그리고 항목집합의 조인을 위해 저장하는 항목의 prefix 유틸리티 pu(X)를 저장한다. 그림 2는 1-item에 대한 utility-list 구조를 표현한 것이다. 1-item 항목의 pu(X)는 0으로 초기화한다.
마이닝 과정에서 발견되는 항목집합의 유형은 세 가지이다. 첫째는 항목집합 자체의 유틸리티가 임계치를 만족하여 높은 유틸리티 항목집합이 되는 경우, 둘째는 높은 유틸리티 항목집합이 되지는 않지만 다른 항목과 조인연산을 통해 높은 유틸리티 항목집합이 될 가능성이 있는 항목집합으로 식별되는 경우, 셋째는 높은 유틸리티 항목집합이 아니고, 조인 가능한 항목집합도 되지 않는 경우로 구분된다. 여기서 높은 유틸리티 항목집합의 식별은 유틸리티-리스트에서 u(X)값으로 식별하고, 조인가능한 항목집합의 식별은 u(X)와 ru(X)의 합이 임계값을 만족하는지의 여부로 식별한다. 그리고 항목집합의 u(X)와 ru(X)의 합이 최소 임계치를 만족하지 못하면 마이닝 과정에서 제외된다.
마이닝 과정을 표 3의 트랜잭션을 이용하여 높은 유틸리티 항목집합이 생성되는 과정을 일부의 항목을 이용하여 설명한다.
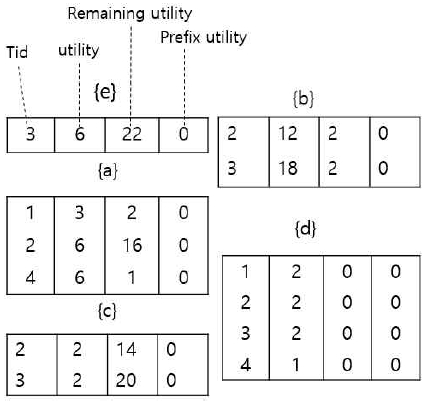
1-item a와 c을 조인한 2-item ac에 대한 조인연산을 하기에 앞서 조인했을 때 높은 유틸리티 항목집합이 될 가능성을 미리 체크한다. 조인 가능성을 체크하기 위해 항목을 포함하고 있는 트랜잭션들에 대해 비트 AND 연산을 이용한다. 그리고 연산 결과로 1이상이 되고, 이들 공통 트랜잭션(Tj) 에 대한 TWU(X)=∑TU(Tj) ≥ min_util을 만족하면 높은 유틸리티 항목집합이 될 가능성이 있다고 판단하여, 이 항목집합에 대한 유틸리티-리스트 구조를 생성한다.
그림 3의 (a)에서 항목 a와 c를 포함하는 트랜잭션들에 대해 비트 AND 연산을 수행하면 bit(e) ^ bit(c) = 0100 ≥1 이고, 이들 항목을 공통으로 포함하는 트랜잭션의 TU(T2)=22 ≥ min_util=20.7 만족하므로 조인 항목집합 ac에 대한 유틸리티-리스트를 구성한다. 항목집합 ac의 유틸리티-리스트에서 ru(ac)는 트랜잭션 T2에서 항목집합 ac 이후에 나타나는 항목들의 유틸리티 합, ru(ac)= u(b) +u(d)=14 이고, 항목집합 ac의 prefix 항목 a를 나타내는 pu(ac) = u(a) = 6 이다. 그림 3의 (a)에서 u(ac)=8이므로 높은 유틸리티 항목집합이 되지 못한다. 그러나 u(ac)+ru(ac)=22 ≥ min_util 으로 조인 가능한 항목이 되어 마이닝 대상 항목이 된다. 그림 3의 (b)의 항목집합 cb의 u(cb)=34 ≥min_util 이고, (c)의 항목집합 u(bd)=34≥min_util 이므로 높은 유틸리티 항목집합이 된다. (d)의 항목집합 u(acb)=20는 임계치를 만족하지 못하므로 높은 유틸리티 항목집합이 되지 못한다.
그림 3의 (e)는 2-item의 항목 cb와 bd의 트랜잭션에 비트 AND 연산에서 bit(cb) ^ bit(bd) = 0110 ≥1 이고, TU(T2) + TU(T3)=50 ≥ min_util 만족하므로 조인연산을 통한 3-item의 cbd에 대한 유틸리티-리스트 구조를 보여준다. u(cbd, T2)=u(cb, T2)+u(bd, T2)-pu(bd, T2)=14+14-12=16, u(cbd, T3)=u(cb, T3)+u(bd, T3)-pu(bd, T3)=20+20-18=22, u(cbd, T2)+ u(cbd, T3)=38 ≥ min_util 이므로 항목집합 cbd는 높은 유틸리티 항목집합이 된다. 이와 같은 항목집합의 조인연산을 통해 (f)의 4-item acbd는 u(acbd)=22 ≥min_util 이므로 높은 유틸리티 항목집합이 된다. 마이닝 과정은 더 이상 조인할 항목집합이 없을 때 수행한다. 이에 대한 알고리즘을 나타낸 것이 그림 4이다. 알고리즘 1은 1-item에 대한 유틸리티-리스트를 초기화하는 과정이고, 알고리즘 2는 초기화된 1-item 의 유틸리티-리스트의 조인을 통해 n-item 유틸리티-리스트를 생성한다.
Ⅳ. 실험 평가 및 분석
이 논문에서 제안한 알고리즘(UL-HUM)의 성능을 평가하기 위하여 HUI-Miner 알고리즘(HUI)[13]과 비교하여 평가하였다. 실험을 위해 IBM Quest Data Generator로 생성한 T10I1000D100K 데이터에 아이템별 유틸리티 값을 1에서 100까지 랜덤하게 추가하여 생성된 데이터 셋을 사용하였다. 각 데이터 셋의 트랜잭션 수는 100K이며, 아이템 수는 1K에서 4K까지로 구성되어져 있다. 트랜잭션의 평균 길이는 10개로 구성되어 있다. 최소 유틸리티 임계값 s을 0.01%에서 0.1%까지 변화시키며 실험하였다.
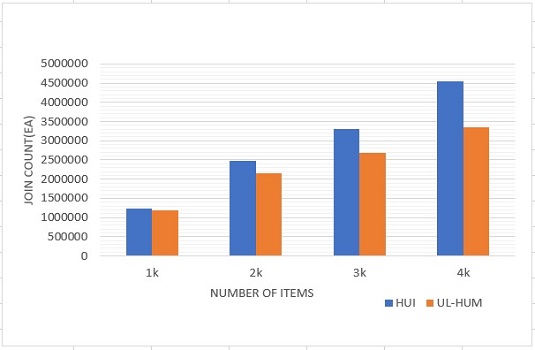
첫 번째 실험에서는 아이템의 수에 따른 Join count의 수를 비교하였고, 그림 5는 최소 유틸리티 s=0.01%인 경우에 대한 결과를 나타낸다. 항목의 수가 작은 1K의 경우, HUI와 UL-HUM는 약 44*103의 차이를 나타내고 있으며, 항목의 수가 큰 4K의 경우 1.2*106의 차이를 나타내고 있다. 이러한 결과는 항목의 수가 많을수록 전체적인 1-item의 높은 유틸리티 항목의 비율은 줄어들지만, 전체적인 개수 자체는 증가하므로, 높은 유틸리티 항목들의 조인은 증가하게 된다. HUI과 비교해 UL-HUM 기법은 각 항목을 가지는 트랜잭션의 정보를 비트로 저장하고 있으므로, 전체 트랜잭션에 대한 비교를 수행하지 않고, 각 항목이 공통 트랜잭션이 있는 경우만 수행하므로 Join count를 크게 줄이는 효과가 있다.
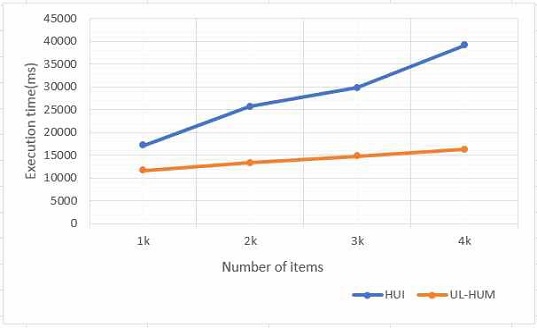
데이터 항목에 따른 실행 시간을 그림 6과 같이 비교하였다. 그림 6은 최소 유틸리티 s=0.01%일 때의 결과로, 아이템의 수가 1K에서 4K까지의 데이터에 대한 실행시간을 보여준다. 이 결과는 이 논문에서 제안한 UL-HUM 기법이 HUI 기법보다 최소 1.4배에서 2.4배까지 빠르게 수행됨을 보여주었다. 이러한 결과는 UL-HUM 기법이 Join Count의 수를 대폭 줄임으로 써, 불필요한 비교 연산을 대폭 줄인 결과로 인한 것으로 판단된다.
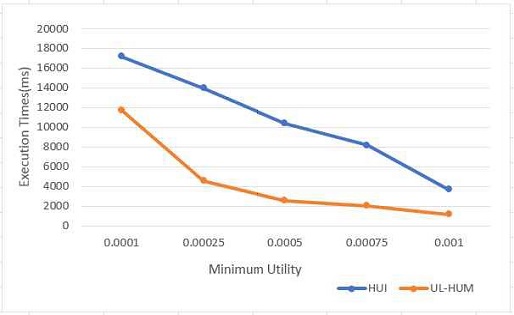
그림 7은 최소 유틸리티에 따른 실행시간을 보여준다. 이 결과는 모든 데이터 셋에서 최소유틸리티가 낮을수록 UL-HUM가 HUI보다 실행 속도가 최소 1.4배에서 최대 2.4배 빠름을 보여주고 있다. 이 결과는 또한 최소 유틸리티가 높아질수록 높은 유틸리티 항목의 수가 줄어들게 되고, 따라서 Join count의 수가 급격히 줄어들게 되므로, UL-HUM와 HUI의 성능이 비슷해지는 경향을 보였다.
이 실험을 통하여 UL-HUM는 항목*트랜잭션 수만큼의 추가적인 bit를 유지해야 하므로 HUI보다 메모리는 더 소모되지만, 항목 수가 많고, 높은 유틸리티 항목이 많은 경우 HUI보다 최대 2.4배 빠른 실행속도를 보여 주었다.
Ⅴ. 결 론
높은 유틸리티 항목집합을 마이닝 하기 위해 이 논문에서는 유틸리티-리스트 구조를 이용하였고, 항목의 조인 연산비용을 줄이기 위해 Prefix 항목의 유틸리티 정보를 리스트 구조에 저장하였다. 그리고 공통 항목을 포함하는 트랜잭션을 빠르게 검사하기 위해 비트연산을 이용하는 방법을 제안하였다. 실험을 통해 우리가 제안한 알고리즘이 1-item 수가 많을수록 조인 연산비용을 줄이는 데 더 큰 효과가 있음을 알 수 있었고, 이것은 같은 항목을 포함하는 트랜잭션의 검사를 위해 비트 연산을 이용하는 것이 효율적임을 입증한다. 결과적으로 이 논문에서 제안한 알고리즘은 항목 종류의 수가 많은 경우, 그리고 높은 유틸리티 항목이 많은 경우에 특히 효과적이다. 그러나 메모리 측면에서는 성능을 더 개선시키는 연구가 필요하다. 그러므로 메모리와 실행시간을 모두 고려하는 효율적인 알고리즘의 연구가 계속 진행될 것이다.
Acknowledgments
이 논문은 2019년도 남서울대학교 학술연구비 지원에 의해 연구되었음.
참고문헌
-
R. Agrawal, T. Imielinski, and A. Swami, "Mining association rules between sets of items in large databases," in Proc. ACM SIGMOD Int. Conf. Manage. Data, pp. 207–216, 1993.
[https://doi.org/10.1145/170036.170072]

- R. Agrawal and R. Srikant, "Fast algorithms for mining association rules," in Proc. 20th Int. Conf. Very Large Databases, pp. 487–499, 1994..
-
J. Han, J. Pei, and Y. Yin, “Mining frequent patterns without candidate generation,” in Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, pp.1-12, 2000.
[https://doi.org/10.1145/335191.335372]

-
H. Ryang, U. Yun, "Performance Analysis of Sliding Window based Stream High Utility Pattern Mining Methods," Journal of Computer and Science, 17(6), pp.53-59, 2016.
[https://doi.org/10.7472/jksii.2016.17.6.53]

- J. Su, W. Chang, V. Tseng, "Integrated mining of social and collaborative information for music recommendation," Data Science Patterns Recognition, 1(1), pp.13-30, 2017.
-
W. Wang, J. Yang, and P. Yu, “Efficient mining of weighted association rules (WAR),” In Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining , Boston, pp. 270-274, 2000.
[https://doi.org/10.1145/347090.347149]

-
F. Tao, F. Murtagh, and M. Farid, “Weighted association rule mining using weighted support and significance framework,” In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, pp. 661-666, 2003.
[https://doi.org/10.1145/956750.956836]

-
U. Yun, D. Kim, "Mining of High Average-utility Itemsets using novel list Structure and pruning Strategy," Future Generation Computer System, 68, pp.346-360, 2017.
[https://doi.org/10.1016/j.future.2016.10.027]

- H. Yao, H. J. Hamilton, and L. Geng, “A unified framework for utility-based measures for mining itemsets," in Proc. ACM SIGKDD 2nd Workshop Utility-Based Data Mining, pp. 28-37, 2006.
-
Y. Liu, W. Liao, and A. Choudhary, “A two-phase algorithm for fast discovery of high utility itemsets,” in Proceedings of the 9th Pacific-Asia Conference on Knowledge Discovery and Data Mining, Springer, Vol. 3518, pp. 689-695, 2005.
[https://doi.org/10.1007/11430919_79]

-
C. F. Ahmed, S. K. Tanbeer, B.-S. Jeong, and Y.-K. Lee, “Efficient tree structures for high utility pattern mining in incremental databases,” IEEE Transactions on Knowledge and Data Engineering, Vol.21, No.12, pp.1708-1721, 2009.
[https://doi.org/10.1109/TKDE.2009.46]

-
H. Yao, H. J. Hamilton, “Mining itemset utilities from transaction databases,” Data and Knowledge Engineering. SIAM, Vol. 59, pp.603-626, 2006.
[https://doi.org/10.1016/j.datak.2005.10.004]

-
V. S. Tseng, B.-E. Shie, C.-W. Wu, and P. S. Yu, “Efficient algorithms for mining high utility itemsets from transactional databases,” IEEE Transactions on Knowledge and Data Engineering, Vol.25, No.8, pp.1772-1786, 2013.
[https://doi.org/10.1109/TKDE.2012.59]

-
U. Yun, H. Ryang, and K. H. Ryu, “High utility itemset mining with techniques for reducing overestimated utilities and pruning candidates," Expert Syst. Appl., vol. 41, no. 8, pp. 3861-3878, 2014.
[https://doi.org/10.1016/j.eswa.2013.11.038]

-
S. Dawar and V. Goyal, “UP-Hist tree: An efficient data structure for mining high utility patterns from transaction databases," in Proc. 19th Int. Database Eng. Appl. Symp., pp. 56-61, 2015.
[https://doi.org/10.1145/2790755.2790771]

- J. Liu, K.. Wang, B. C. M. Fung, "Mining High Utility Patterns in One Phase without Generating Candidates,“ IEEE Transaction on Knowledge and Data Engineering, Vol.27, 2015.
-
M. Liu and J. Qu, “Mining high utility itemsets without candidate generation,” in Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, pp.55-64, 2012.
[https://doi.org/10.1145/2396761.2396773]

-
P. Fournier-Viger, C.-W. Wu, S. Zida, and V. S. Tseng, “FHM: Faster high-utility itemset mining using estimated utility co-occurrence pruning,” Foundations of Intelligent Systems, Springer, pp.83-92, 2014.
[https://doi.org/10.1007/978-3-319-08326-1_9]

저자소개

2001년 :충북대학교 전자계산학과 (이학석사)
2005년 :충북대학교 전자계산학과 (이학박사)
2001년~2006년: 정우시스템(주) 연구소장
2006년~현 재 : 남서울대학교 컴퓨터소프트웨어학과 교수
※관심분야:데이터 마이닝(Data Mining), 빅 데이터 분석(Big Data Analysis), 딥러닝(Deep Learning) 등