시간 간격 기반의 빈발패턴 항목 탐사

Ⅰ. 서 론

데이터 마이닝은 대용량의 데이터에 숨겨진 의미있고 유용한 패턴과 상관관계를 추출하여 의사결정에 활용하는 작업이다. 정보기술의 발전으로 매일 쏟아져 나오는 데이터의 양은 방대해졌다. 데이터의 양이 급속도로 증가함에 따라 그 안에 담긴 의미있는 정보를 찾아 활용하는 일이 쉽지 않다. 따라서 방대한 양의 데이터 속에 존재하는 유용한 패턴과 상관관계를 찾아내기 위한 데이터 마이닝 기법의 연구가 지속적으로 이루어지고 있다[1], [2].

연관규칙은 트랜잭션에 존재하는 항목들간의 연관관계를 발견하는 것이다[3], [4]. 트랜잭션에 존재하는 각 항목들은 발생하는 시간의 간격주기를 가질 수 있다. 즉, 데이터베이스 전체에서는 빈발하지 않지만 특정 기간 동안에는 빈발한 항목이 있을 수 있다. 이러한 특정한 시간 간격주기를 갖는 데이터에 대한 마이닝은 계절적, 시기적, 공간적 특성을 갖는 데이터에 대한 특별한 의미가 있을 수 있다.

빈발 패턴(frequent pattern)은 데이터 집합에서 빈번하게 발생하는 항목들이다. 빈발 패턴을 발견하는 것은 데이터 사이의 연관성 그리고 우리가 알지 못했던 데이터간의 흥미로운 관계를 탐사하는 기본적인 역할을 한다. 빈발 패턴 마이닝은 데이터 마이닝 분야에서 가장 많이 연구되는 분야로써 우리 주변에서 가장 널리 활용되는 있다[5], [6].

모든 데이터는 시간정보를 기반으로 발생하며 시간 정보가 고려된 데이터 마이닝은 실세계의 응용에서 중요하다. 타임 스탬프된 이벤트 시퀀스는 (이벤트, 발생시각)의 순차적인 서열로 나타내고 이들 시퀀스 이벤트를 대상으로 이벤트들의 연관 관계와 패턴을 검색하는 연구들이 있다. 이들 연구는 타임 시리즈 분석, 단백질 구조 예측, 네트워크 침입 탐지와 같은 응용에 사용된다[7], [8]. 일반적인 연관규칙에서 시간적인 규칙에 따라 사건이 발생된다면 순차패턴 규칙이라 한다[9]. 즉 “A→B는 상품 A가 구매되면 일정시간이 경과한 다음 상품 B가 구매된다“ 라는 관계를 갖는다. 축적된 이벤트 시퀀스에 대해 데이터마이닝을 통하여 이벤트 발생에 대한 인과관계의 연관규칙을 탐사함으로써 과거의 데이터를 바탕으로 미래 발생 가능한 이벤트를 예측할 수 있는 유용성을 갖는다.

이 논문에서 우리는 시간정보를 포함하는 데이터베이스에 대해 일정한 수의 트랜잭션으로 이루어진 시간 간격을 구분하고, 각 시간 간격단위에 포함된 트랜잭션들에 대한 연관관계를 탐사하는 데이터 마이닝 기법을 제안한다. 이를 위해 사용자에 의해 미리 주어진 기본적인 시간간격에 대해 각 시간단위에서 빈발한 연관 항목을 발견하고, 연속적인 시간 간격단위는 그룹핑되어 확장되므로 계층적인 구조가 형성하며, 그룹핑된 각 시간간격에서 빈발한 연관항목집합을 발견한다. 시간 간격단위의 그룹핑을 통해 연관항목집합을 발견하므로 작은 단위의 시간단위에서의 빈발 항목뿐만 아니라 사용자가 원하는 임의의 시간 간격단위에 대한 연관항목집합 추출도 가능하다.

이 논문의 구성은 다음과 같다. 2장에서는 제안하는 알고리즘과 관련된 연구들을 기술하고, 3장에서는 마이닝을 위한 기본 개념의 정의와 빈발항목을 탐사하는 마이닝 알고리즘을 설명한다. 4장에서는 기존의 알고리즘과의 비교 실험을 통해 제안하는 알고리즘의 효율성을 분석한다. 마지막으로 5장에서 결론을 맺는다.

Ⅱ. 관련연구

데이터 마이닝 기법 중의 하나인 연관규칙은 한 항목들이 그룹과 다른 항목들의 그룹 사이에 강한 연관관계가 있음을 보여주며, 순차패턴은 연관규칙에 시간이라는 개념을 고려하여 순차적으로 발생될 가능성이 큰 항목집합을 찾아낸다. 순차패턴은 환자 이력, 구매 이력, 로그 이력 등 다양한 이력 데이터에 숨겨진 지식을 탐사한다. 이력은 이벤트들의 시퀀스이며 이벤트는 발생 시점 및 종료 시점과 같은 시간 속성을 갖는다. 따라서 축적된 이벤트 데이터베이스가 있다면 데이터 마이닝을 통하여 이벤트 발생에 대한 인과관계에 대한 연관규칙을 탐사함으로써 과거의 데이터를 바탕으로 미래 발생 가능한 이벤트를 예측할 수 있는 정보로 활용될 수 있다[7].

빈발 에피소드(frequent episode) 탐사[10]는 일련의 사건 시퀀스(event sequence) 데이터로부터 빈번하게 발생하는 에피소드를 찾는 순차패턴 기법이다. 에피소드는 빈번하게 발생하는 특정 사건 시퀀스를 정의하며, 시퀀스를 구성하는 사건은 서로 밀접하게 관련된 사건이다. 탐사하는 과정은 사용자가 지정한 윈도우 크기를 갖는 시간 윈도우들의 집합에서 에피소드가 발생한 윈도우의 비율이 최소 발생 임계치(frequent threshold)이상을 만족하는 모든 빈발 에피소드를 찾는 것이다. 예를 들어 매초마다 발생한 사건 시퀀스 {c, e, f, b, d, a, c, e, g}에 대해 시간 윈도우 크기를 3초, 최소 발생 임계치를 50%라 할 때, (c, e)는 세 개 윈도우 중에 두 개의 윈도우에서 발생하였으므로 빈발 에피소드이다.

시간 데이터 마이닝(temporal data mining)은 기존 데이터 마이닝에 시간 개념을 추가하여 시간 의미와 시간 관계를 가지는 유용한 시간 지식을 탐사하기 위한 데이터 마이닝 연구분야이다. 시간 데이터 마이닝을 통해 환자의 병력, 상품 구매이력, 웹 로그 등과 같은 시간 데이터로부터 다양한 형태의 시간 지식을 찾을 수 있다. 예를 들면 “빵을 사는 사람은 우유를 함께 산다“와 같은 기존의 연관규칙 뿐만 아니라, ”매년 6월~8월 동안 기저귀를 사는 사람의 70%가 맥주를 함께 산다“와 같은 시간 의미를 갖는 연관규칙을 찾아낼 수 있다. 그리고 ”2017년도 이전에는 A특성을 가진 고객이 우량 고객일 가능성이 높으나 2018년 현재와 미래에는 가능성이 낮다“와 같이 시간 제약조건을 가진 분류규칙도 발견할 수 있다.

시간 연관규칙 탐사기법은 연관규칙 탐사, 분류, 특성화와 같은 기존의 데이터 마이닝 기법을 확장한 기법으로 시간 관계와 인과관계에 대한 시간 연관규칙을 탐사한다. 그리고 시간 연관규칙 탐사기법은 반복되는 연관규칙을 발견하기 위한 순환 연관 관계 탐사와 캘린더 형태로 표현된 시간 패턴에 대한 연관규칙을 발견하는 캘린더 연관 관계 탐사[11]를 포함한다.

[7]에서는 인터벌을 지닌 이벤트에 대한 시간 관계 규칙 탐사 방법을 제안하였다. 이 방법은 원시 데이터에서 한 번의 스캔을 통해 이벤트의 인터벌을 이벤트의 시작 시점과 종료시점으로 표현된 인터벌 이벤트로 요약한다. 그리고 요약된 인터벌 이벤트에서 Allen의 시간 관계 연산자를 이용해 연관규칙을 탐사한다. 이러한 시간 데이터 마이닝에 대한 연구는 이벤트에 대한 트랜잭션의 발생 시점만을 고려하며, 연속적인 시간 단위에서의 빈발한 데이터의 분석은 이루어지지 않는다. 이벤트 발생의 인과 관계에 대한 초점이 아니더라도 특정한 시간단위에서 유용한 데이터를 발견하는 일은 실세계에서 중요하다.

데이터 마이닝 기법중에 계층적 클러스터링 방법이 있다. 계층적 구조를 이루는 2가지 형태가 있는 데 agglomerative 계층적 방법과 divisive 계층적 클러스터링 방법이 있다. 우리가 제안하는 시간간격의 그룹핑에 대한 구조는 가장 작은 단위의 atomic 클러스터들을 그룹핑하면서 더 큰 클러스터로 확장해 가는 상향식(bottom-up) 방식의 agglomerative 계층적 클러스터링 방법[12]과 구조가 유사하다.

Ⅲ. 시간 간격 기반의 빈발 항목집합 마이닝

이 논문에서는 시간 간격단위를 기초로 일정한 수의 트랜잭션에 포함되어 있는 빈발 항목집합을 탐사한다. 원시 데이터에서 관심있는 항목 또는 사용자가 지정한 최소 임계치를 만족하는 데이터 항목을 필터링하여 초기 데이터를 생성한다. 마이닝을 위한 기본 정의는 다음과 같다.

정의 1. 시간 데이터 트랜잭션(Temporal data transaction)

Temporal data transaction은 시간의 흐름에 따라 발생하는 데이터를 포함하는 트랜잭션을 T로 표기하고, 일련번호를 부여한다. T = {T₁, T₂, T₃,..,T_i,..T_n}에서 T_i은 i번째 트랜잭션을 의미한다. 각 트랜잭션은 항목들을 포함하며 항목집합을 Itemset(I)로 정의하고, I = {I₁, I₂, I₃,..,I_n}로 표현한다. 항목 I_k은 k번째 항목이다.

정의 2. 항목 지지도(Item support)

동일한 level의 동일한 일련번호를 갖는 TP_v.s(Time Period)의 그룹핑에 포함된 모든 트랜잭션에 대해 해당 항목을 포함하고 있는 트랜잭션의 수(Num)를 항목 지지도로 정의하고 Supp(I_i)로 표기한다.

정의 3. 최소 지지도(min_sup)

최소 지지도는 각 hierarchical time level에 그룹핑된 TP_v.s에 포함되어 있는 모든 트랜잭션의 수에서 해당 항목을 포함하고 있는 트랜잭션 수의 비율(%)이 만족해야 하는 최소값을 의미한다.

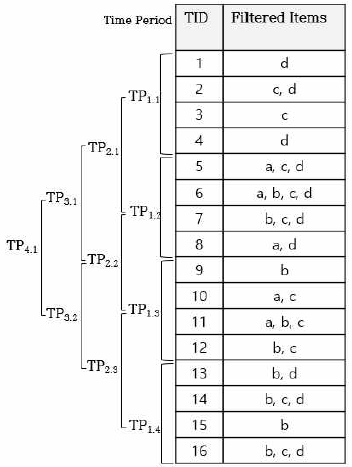
이 논문에서 제안하는 마이닝 알고리즘에서는 시간 간격(Time Period)을 기반으로 한다. 시간 간격은 TP로 표기하고, TP에는 일정 개수의 트랜잭션을 포함한다. TP의 크기를 |TP|로 표기한다. 예를 들어, 하나의 TP에 포함된 트랜잭션의 수가 3이면 |TP|=3이다. TP는 레벨과 시퀀스 정보를 포함하여 TP_v.s으로 표현하다. 여기서 v는 TP를 그룹핑하는 계층 레벨을 의미하고, s는 같은 level에서의 일련번호를 의미한다. TP를 그룹핑할 때는 같은 level의 일련번호를 이용하여 그룹핑한다. 그림 1은 TP를 그룹핑하는 구조의 예를 보여준다. 그룹핑 된 TP의 레벨과 시퀀스 표현은 TP_n.s=TP_n-1,s∪TP_n-1.s+1 이다.

Fig. 1.

Grouping structure of time period

Frequent itemset(FrqIS)을 발견하는 방법은 level.1의 각 basic time period에서 최소지지도를 만족하는 빈발한 itemset을 추출하고, level.1 TP의 그룹핑을 통하여 level.2의 TP를 구성한다. level.1 TP에서 추출한 빈발한 항목들을 union하여 level.2의 TP의 항목이 되고, 그룹핑된 TP의 time period에서 공통으로 빈발한 항목들을 탐사한다. 이와 같은 방법으로 level.2의 TP를 그룹핑하여 level.3 TP에서 빈발한 항목들을 탐사한다. 이러한 과정은 더 이상 그룹핑할 TP가 존재하지 않을 때까지 수행하며, 결과적으로는 부분뿐만 아니라 전체의 DB에 대한 빈발항목들도 탐색된다. 빈발항목의 탐사에서 우리는 후보항목 생성 시간을 줄이기 위하여 매트릭스를 구성하는 Eclat 알고리즘[13]을 이용한다. TP전체에 포함되어 있는 항목들을 열로 표현하고, 해당 항목을 포함하는 트랜잭션, TID를 행으로 구성하여 매트릭스를 구성한다. 이 매트릭스 정보를 이용하여 각 TP에서 최소 빈발도를 고려한 빈발 항목들을 전처리하고, 전처리된 level.1 항목들의 예를 그림 1에서 보여준다.

Level.1 의 빈발항목으로 구성된 TP 들을 그룹핑하여, 그룹핑된 TP에서 빈발항목들을 탐사한다. 예를 들어, TP의 크기 |TP|=4 인 경우, TP_1.1과 TP_1.2에 포함된 전체 8개의 트랜잭션에서 빈발한 연관 항목을 발견하여 TP₂₁에 저장한다. 즉, TP_1.1과 TP_1.2에서 빈발한 항목들을 union하고 이들에 대한 min_sup을 만족하는지 check 하여 빈발항목의 여부를 결정한다. 다음으로 TP_1.2와 TP_1.3에서 공통으로 빈발한 항목을 추출하여 TP_2.2에 저장한다. 이와 같은 방법으로 level.1의 TP_1.s와 TP_1.s+1에서(1≤s and s≥n-1) 빈발한 연관 항목을 발견하여 level.2의 TP_2.s 시퀀스에 저장한다. 그리고 level.2 빈발항목의 TP 시퀀스를 그룹핑하여 level.3 TP_3.s 시퀀스를 생성한다. 이 방식은 time period를 점차 확장하는 방식으로 hierarchical TP level 시퀀스가 구성되고, 결과적으로 전체에 TDB 포함된 트랜잭션에 대한 빈발 항목을 탐사하는 결과를 생성한다.

그림 1의 예제 DB에 대해 min_sup= 0.5 가정하여 마이닝 과정을 설명한다.

TP_1.2의 일부항목에 대한 지지도의 예를 들면, Supp(a) = 3/4, Supp(c) = 3/4, Supp(ac) = 2/4, Supp(bd) = 2/4 이므로 min_sup를 만족하여 a, c, ac, bd 은 빈발항목이며, 표 1에서 각 level.1 TP에 대한 빈발항목들을 보여준다. level.1 TP 시퀀스는 그룹핑을 통하여 level.2의 TP 시퀀스를 생성한다. 예를 들면, TP_1.1과 TP_1.2를 그룹핑하여 level.2의 TP_2.1를 생성하기 위하여 level.1 TP 시퀀스에서의 빈발항목을 union하면, FrqIS(TP_1.1) ∪ FrqIS(TP_1.2) = {a, b, c, d}이고, 이것이 후보항목이 된다. 그리고 이들에 Supp(I_i)를 계산하여 min_sup의 만족여부를 체크하고, 빈발항목 여부를 결정한다. 빈발항목이 결정되면 이들이 FrqIS(TP_2.1)의 항목이 된다. 이와 같은 방법으로 time period에 속한 TP 시퀀스를 그룹핑하여 level를 증가시키면서 빈발항목들을 결정한다.

Table 1.

TP1 Frequent ItemSets(FrqIS)

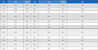
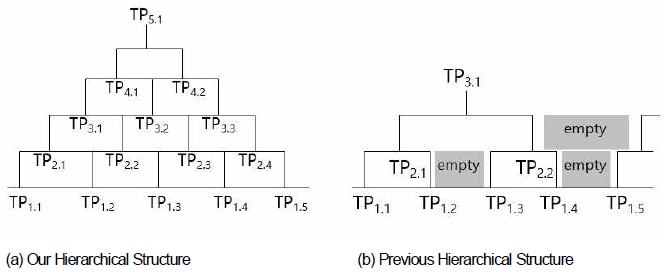
이 논문에서 제안하는 Hierarchical time period(HTP) 구조와 유사한 기존연구 [14]를 그림 2에서 보여준다. 그림 2의 (a)는 이 논문에서 제안하는 Hierarchical time period 구조이고 (b)는 기존 논문 [14]에서 제안한 Hierarchical time granule 구조이다. 이 논문에서 제안하는 (a)의 구조는 각 level에 있는 모든 TP 시퀀스를 그룹핑하면서 time period를 확장하는 방식의 구조이므로 그룹핑된 시간간격의 단위가 연속적으로 이어져 있어서 시간의 흐름에 따라 탐색된 빈발 항목 변화의 모니터링이 가능하고, 어느 구간에서든지 데이터의 request나 분석이 필요한 구간에서 데이터 손실없이 return할 수 있는 구조이다. 반면에 (b)의 구조는 time period의 그룹핑을 연속적으로 구성하지 않고 TP를 쌍(pair)의 단위로 그룹핑하여 그림 2의 (b)에서와 같은 empty 부분이 발생하게 된다. 예를 들면, empty 부분인 TP_1.2∼TP_1.3의 시간 구간에 대한 빈발항목 탐사가 이루어지지 않아 정확한 빈발항목의 탐색이 어렵다. (a)의 구조가 (b)의 구조보다 더 dense 한 구조를 갖기 때문에 hierarchical level이 더 많아지고 마이닝 수행시간은 더 많이 소요될 수 있지만 시간의 흐름에 따른 빈발 항목의 데이터 분석에는 더 정확하고 유용한 정보를 얻을 수 있다. 또한 [14]에서 빈발항목을 탐색하기 위한 임계값으로 상대적인 최소지지도(min_rsup)를 이용하였다. 상대적인 지지도는 해당 항목이 처음 발생한 TP단위의 트랜잭션 수에 대한 항목의 발생빈도 비율을 적용한다. 빈발항목 탐색에서 상대적인 지지도를 이용하는 것과 일반적인 min_sup를 적용한 경우의 차이점을 보면, 같은 time period 에 대한 frequent items의 탐색 결과가 달라질 수 있다. TP_1.2에서 min_sup를 적용할 때 같은 period 내의 모든 트랜잭션 수에 대한 해당 항목을 포함하는 트랜잭션의 수의 계산에서는 Supp(b) = 2/8 이 되므로 min_sup를 만족하지 못하여 빈발 항목이 되지 않는다. 그러나 상대적 지지도를 적용하면 rsup(b) = 2/4가 되므로 min_rsup를 만족하여 빈발 항목이 된다. 아래 그림 3 (a)의 min_rsup를 적용한 경우의 예를 들면, TP_1.1에서는 min_rsup를 만족하지 못했지만 TP_1.2에서 min_rsup를 만족한 빈발 항목은 TP_1.1와 TP_1.2를 그룹핑한 TP_2.1에서 빈발 항목이 되는 경우가 많아진다. 즉, 상대적 지지도를 적용하면 TP_2.1에서의 빈발항목은 TP_1.2에서만 빈발한 항목이 TP_1.1∼TP_1.2 에서 공통으로 빈발한 것처럼 처리될 수 있고, 이것은 지속적으로 다음 level의 time period의 빈발 항목 탐사에도 지속적으로 영향을 미친다. 반면 일반적인 Supp에 의해 탐색된 그림 3 (b)의 TP_2.1의 빈발항목은 각 TP_1.1와 TP_1.2에서 빈발한 항목의 union, 즉 FI(TP_1.1)∪FI(TP_1.2) 에 의해 빈발항목을 탐색하므로 TP_1.1∼TP_1.2에서 공통으로 빈발한 항목을 탐색한다. 결과적으로 상대적 지지도를 적용할 때와 일반적인 지지도를 적용할 때 탐색되는 빈발 항목의 결과는 달라진다. 즉, 상대적 지지도의 적용은 basic time period 단위의 level.1에서 특정 시간에 대한 빈발 항목을 탐색할 때 유용하게 적용될 수 있지만 레벨이 증가할수록 발견할 수 있는 빈발항목에서 제외될 수 있다.

Fig. 2.

Grouping Structure

Fig. 3.

Discovering range of frequent items by min_rsup and min_sup

Ⅳ. 실험

이 장에서는 우리가 제안하는 알고리즘 HTP(Hierarchical Time Period)의 성능을 평가하기 위하여 기존의 HTAR(Hierarchical Temporal Association Rule) 알고리즘[14]의 비교를 통한 실험 결과를 기술한다. 실험환경은 Window 10, 8GB RAM, 3.30GHz CPU 환경에서 R로 수행하였다. 실험 데이터 셋은 R의 데이터 생성기를 이용하였다. 트랜잭션당 평균 아이템수를 10개로 설정하고 10K개의 트랜잭션을 생성하였다. 아이템의 수에 따른 성능을 평가하기 위하여 총 아이템 수는 100 ~ 4000개의 데이터 셋을 생성하였다. 예를 들면 T10I1000D10K 데이터셋은 1000개의 아이템으로 구성된 10K 데이터 셋을 의미한다. 트랜잭션의 수를 625로 할 경우 10K 데이터셋에서는 16개의 기본 간격단위가 생성된다.

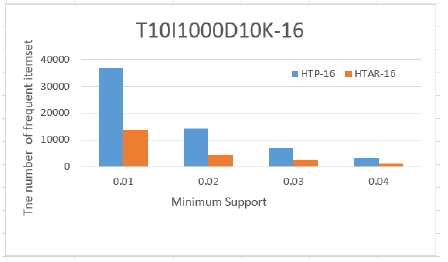
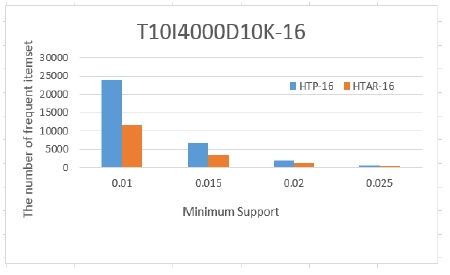
우리는 최소지지도에 따라 생성되는 빈발항목의 수를 비교하였다. 그림 4와 그림 5는 데이터셋 T10I1000D10K와 T10I4000D10K에서 time periods가 16인 경우, 최소지지도가 0.01에서 0.04까지 변화하면서 수행한 결과를 보여준다. 실험 결과에서 알 수 있듯이 이 논문에서 제안된 HTP알고리즘이 HTAR알고리즘 보다 많은 빈발항목을 생성한다는 것을 볼 수 있다. 최소 지지도가 낮을 때는 기존 알고리즘보다 2배 이상의 빈발항목을 생성하는 것을 알 수 있다. 이는 시간 간격을 구성하는 구조의 차이로 인해 더 많은 빈발 항목을 탐사하는 것으로 판단된다.

Fig. 4.

The number of frequent itemset (T10I1000D10K-16)

Fig. 5.

The number of frequent itemset (T10I4000D10K-16)

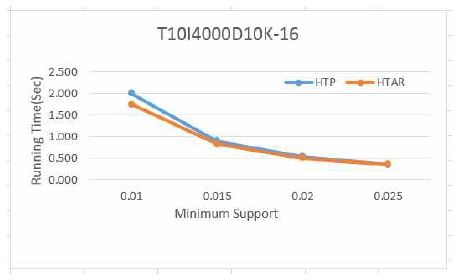
그림 6은 T10I4000D10K의 16 periods에서 최소지지도에 따른 실행시간을 보여준다. 실험결과를 보면 최소지지도가 낮을 때는 HTP 알고리즘의 실행시간이 더 많이 소요되지만 최소지지도가 높아질수록 HTP알고리즘과 HTAR알고리즘의 실행시간이 비슷해지는 것으로 나타났으며, 이는 두 알고리즘 모두 최소지지도가 높아질수록 생성되는 빈발항목 수가 적어지게 됨으로써 나타나는 결과이다.

Fig. 6.

Runtime (T10I4000D10K-16)

실험결과를 요약하면 지지도에 따른 빈발항목의 수는 HTP알고리즘이 HTAR알고리즘보다 평균 2~3배 이상 증가하는 반면, 실행시간은 평균 1.29배와 1.10배의 증가함을 보였다. 따라서 이 논문에서 제안된 HTP알고리즘은 HTAR알고리즘 보다 많은 시간이 소요되지만, 탐사되는 빈발항목의 수는 약 3배 이상 많이 생성한다는 것을 알 수 있다.

Ⅴ. 결 론

이 논문에서는 시간 데이터베이스에서 일정한 사이즈의 트랜잭션을 포함하는 TP(Time Period) 기준으로 빈발항목을 발견하기 위해 TP시퀀스의 계층적 그룹핑을 이용하는 HTP알고리즘을 제안하였다. 그리고 우리가 제안하는 알고리즘의 성능을 평가하기 위하여 기존의 HTAR 알고리즘과 비교하는 실험을 하였고, 실험 결과를 통해 제안하는 알고리즘은 기존알고리즘과 비교할 때 수행시간은 1.2배 정도 더 많이 소요되지만, 추출된 빈발항목의 수는 3배 더 많이 탐색이 되는 것을 알 수 있었다. 따라서 우리가 제안하는 알고리즘은 시간의 흐름에 따른 빈발항목 변화의 탐색에 효과적이고, 특정 시간 영역에 대해 빈발항목을 추출해야 하는 네트워킹 관련 프로토콜 및 데이터 교환 트래픽 데이터, 통행량의 조절, 장애 처리, 침입 탐지 등 데이터의 변화를 감지해야 하는 응용에 효율적으로 적용될 수 있다.

Acknowledgments

이 논문은 2018년도 남서울대학교 학술연구비 지원에 의해 연구되었음.

참고문헌

• F. WANG, Y-H. Li, "An Improved Apriori Algorithm based on the matrix", International Seminar on Biomedical information engineering, p152-155, (2008).
• J. Chang, and W. Lee, "A Sliding Window Method for Finding Recently Frequent Itemsets over Online Data Streams", Journal of Information Science and Engineering, 20(4), p753-762, (2004).
• C. H. Lee, C. R. Lin, and M. S. Chen, "On mining general temporal association rules in a publication database", The IEEE International Conference on Data Mining, p337-344, (2001).
• J. M. Ale, and G. H. Rossi, "An Approach to Discovering Temporal Association Rules", in Proceedings of the 2000 ACM symposium on Applied computing ACM, (2000). [https://doi.org/10.1145/335603.335770]
• Y. Kim, W. Kim, and U. Kim, "Mining Frequent Itemsets with Normalized Weight in Continuous Data Streams", Journal of Information Processing Systems, 6(1), p79-90, (2010). [https://doi.org/10.3745/JIPS.2010.6.1.079]
• C. K. Leung, and B. Hao, "Mining of Frequent Itemsets from Streams of Uncertain Data", IEEE International Conference on Data Engineering, (2010). [https://doi.org/10.1109/ICDEW.2010.5452736]
• Y. Lee, J. Lee, D. Chai, B. Hwang, and K. Ryu, "Mining Temporal Interval Relational Rules from Temporal Data", Journal of System and Software, 82, p155-167, (2009). [https://doi.org/10.1016/j.jss.2008.07.037]
• L. Sacchi, C. Larizza, C. Combi, and R. Bellazzi, "Data mining with Temporal Abstractions: learning rules from time series", Data Mining and Knowledge Discovery, 15(2), p217-247, (2007). [https://doi.org/10.1007/s10618-007-0077-7]
• J. Pei, J. Han, B. M. Asi, J. Wang, H. Pinto, Q. Chen, U. Dayal, and M. Hsu, "Mining Sequential Patterns by Pattern-Growth: The PrefixSpan Approach", IEEE Transactions on Knowledge and Data Engineering, 16(11), p1424-1440, (2004). [https://doi.org/10.1109/TKDE.2004.77]
• H. Mannila, H. Toivonen, and A. I. Verkamo, "Discovery of frequent episodes in event sequences", Data Mining and Knowledge Discovery, 1(3), p259-289, (1997). [https://doi.org/10.1023/A:1009748302351]
• V. Srinivasan, and M. Aruna, "Mining Association Rules to Discover Calendar Based Temporal Classification", International Conference on Computing, Communication and Networking, p1-12, (2008). [https://doi.org/10.1109/ICCCNET.2008.4787754]
• E. Boudaillier, and G. Hebrail, "Interactive Interpretation of Hierarchical Clustering", Intelligent Data Analysis 2, p229-244, (1998). [https://doi.org/10.3233/IDA-1998-2306]
• M. Zaki, "Scalable algorithms for association mining", IEEE Transaction on knowledge and Data Engineering, 12(3), p372-390, (2000). [https://doi.org/10.1109/69.846291]
• T. P. Hong, G. C. Lan, J. H. Su, P. S. Wu, and S. L. Wang, "Discovery of temporal association rules with hierarchical granular framework", Applied Computing and informatics, 12(2), p134-141, (2016). [https://doi.org/10.1016/j.aci.2016.01.003]