행렬 기반의 시각화를 위한 조밀한 배치 기법

2-1 표 형태의 배치를 활용한 시각화

다차원 자료를 표 형태의 배치로 나타낸 경우는 표 내의 각 칸에 대응되었던 자료의 특성에 따라 크게 두 종류로 분류될 수 있는데, 각 칸에 대응되는 항목이 하나의 대푯값인 경우와 여러 값이 대응되는 경우가 있다. 먼저 한 칸에 하나의 값이 대응되는 사례 중 하나로 인접 행렬[2]이 있는데, 해당 시각화 기법에서는 인접 여부를 각 칸의 배경 색깔로 나타내게 된다. 또한 보다 자세한 정보가 필요한 경우 배경 색깔의 명도와 채도에 그 값을 대응시켜서 간접적으로 정보를 표현한다. 하나의 대푯값이 있을 때 그 수치를 직접적으로 표시할 경우 일반적인 표가 되지만, 상술한 것처럼 각 칸의 배경 색깔을 활용하여 나타낼 경우 히트맵(heatmap)[3]과 유사한 결과가 도출된다. 다음으로는 각 칸에 복수의 값을 나타낸 사례들이 있는데, 그 중에는 글리프(glyph)를 활용[4]하거나, 시계열 자료를 보여주기 위하여 스파크라인(sparkline)[5]으로 작은 차트를 배치한 경우[6]가 있다. 본 연구에서는 위에 언급된 자료의 형태들에 대하여 재배치를 한 결과를 통해 유용성을 확인하고자 한다.

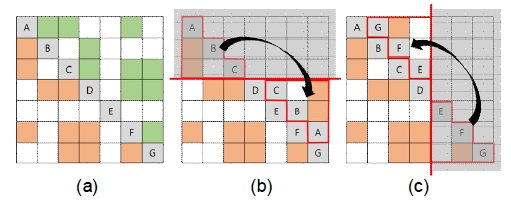
표로 나타내어진 시각화를 행과 열의 특성에 따라서 분류하게 되면 다시 3가지로 분류가 가능하다. 첫 번째로 행과 열에 대응되는 차원 없이 각 칸이 나열되는 경우가 있다. 이러한 경우는 표 내에서 행과 열에 따른 위치가 별다른 의미를 나타내지 않으며, 별도의 순서에 따라 배치되게 된다. 다음으로 다차원 자료에서 행에 대응되는 차원과 열에 대응되는 차원이 다른 경우가 있다. 이는 Perin[7]의 연구에서도 확인할 수 있는 사례로써, 대응될 수 있는 모든 경우의 수를 표의 형태로 표시한 후, 자료를 분석할 때 행 또는 열 내에서의 순서를 바꿔가면서 유의미한 패턴을 찾아낸다. 마지막은 행과 열에 같은 차원이 대응되는 경우로 방향성이 없는 그래프에서의 인접 행렬이 이에 해당한다. 이 경우에는 앞서 언급된 두 가지 시각화와는 달리 같은 순서로 행과 열의 항목들이 배치되었을 때 대각선을 기준으로 그림 1(a)에서 볼 수 있듯이 주황색 부분과 녹색 부분 양쪽이 동일한 정보를 중복하여 표현하게 된다. 본 연구에서는 이와 같은 경우에 대해서 중복되는 정보가 표시될 수 있는 영역을 그림 1(b) 혹은 그림 1(c)와 같이 재배치함으로써 공간 활용도를 향상시키고자 한다.

Fig. 1.

(a) Matrix-based visualization with redundant information (b) relocation of horizontally sliced piece from redundant area (c) relocation of vertically sliced piece from redundant area

2-2 화면상의 공간 절약을 위한 시각화

정보 시각화의 경우 화면의 크기에 제약을 받기 때문에, 크기가 큰 자료를 어떻게 정보를 표현할지에 대한 연구가 여러 각도에서 진행되어 왔다. 이와 관련된 일련의 연구들 중 하나로, 시계열 자료에 대한 표현 방법이 연구되었는데, LiveRAC[8]에서는 다수의 서버에서 수집되는 시계열 자료들을 아코디언 표현법(accordion drawing)[9]을 도입하여 제한된 공간에 나타내었다. 즉, 특이점이 없어서 사용자가 주의를 기울일 필요가 없는 시계열 자료들의 경우 적은 공간을 차지하도록 높이를 줄였고, 이렇게 확보된 공간을 활용하여 사용자가 관심이 있는 자료를 보다 자세히 표현함으로써, 오버뷰(overview)를 보여주면서도 상세 뷰(detail view)를 한 화면에 나타낼 수 있었다. Line Graph Explorer[10]에서는 이와 유사한 방법으로 선 차트(line chart)에 대해서 값의 크기를 색깔로 대응시키고 1 픽셀(pixel) 높이의 선으로 나타냄으로써 최대한 많은 시계열 자료를 보여주고자 했다. 시계열 자료를 보다 조밀하게 표현하는 다른 방법론으로는 제한된 높이에 맞춰 선 차트를 가로 방향으로 길게 분할한 뒤, 띠 형태의 분할된 영역들을 같은 위치에 겹쳐서 배치함으로써 공간을 절약하고자 하는 연구가 있었다[11]. 이러한 horizon graph는 추후 후속 연구[12]를 통해 효율성이 입증되었다. 본 연구에서는 행렬로 나타내어지는 표 형태의 시각화에 대해서 이와 같이 자료를 표시하는 영역 중 중복되는 영역의 일부를 horizon graph에서처럼 재배치했다.

행과 열로 구성된 표 형태의 시각화의 공간 활용 효율성과 관련된 연구 사례로, NodeTrix[13]는 많은 수의 노드를 포함하는 사회 연결망 자료에 대한 인접 행렬 기반의 시각화를 연구하였다. 해당 연구에서는 먼저 군집화(clustering)를 수행한 후, 군집 내에서는 인접 행렬을 그대로 사용하되 군집 간에는 기존 노드-링크(link) 표현법을 사용함으로써 표현 결과에서의 시각적 혼란(visual clutter)을 감소시키고, 불필요한 공간 사용을 줄일 수 있었다. 한편, TileMatrix[14]에서는 행과 열에 같은 항목들이 배치되고, 각 행과 열의 쌍에 대해서 대응되는 값이 존재하는 경우를 다루었다. 해당 연구에서 효율성 증대를 위해 살펴봤던 부분은 행과 열에 동일한 내용이 배치되었을 때 필연적으로 생기게 되는 정보의 중복이었다. 즉, 행 A와 열 B의 쌍에 대응되는 값과 행 B와 열 A의 쌍에 대응되는 값이 동일한 경우를 다뤘는데, 중복되는 삼각형 형태의 영역에 또 다른 행렬의 반쪽을 표시함으로써 활용도를 높이고자 했다. 예컨대 시간의 흐름에 따라 여러 개의 표가 나타나게 되는 경우에 대해서, 각 시점별로 표를 삼각형으로 타일(tile)과 같이 인접하게 배치함으로써 낭비되는 영역을 최소화 하였다. 본 연구 역시 행과 열에 동일한 값이 배치되고 쌍을 이루게 되는 경우에 대해서 중점적으로 다루며, 다만 동일한 행과 열에 대해서 여러 차원을 나타내는 다수의 표가 존재하는 경우가 아니라 하나의 표만 존재할 경우에 대해서 항목들의 재배치를 통해 효율성을 확보하는 방법을 다룬다.

3-1 행렬 내 공간 재배치 기법

본 연구에서는 d3.js[15]를 활용하여 표의 각 칸에 히트맵이나 선 차트를 표시하는 경우에 대해 재배치 기법을 구현하였다. 여기서 제시하는 재배치 기법은 동일한 항목으로 구성된 행과 열을 기준으로 정렬된 경우에 대해서 중복된 정보를 나타내게 되는 영역에 본래 행렬을 일부를 다시 넣는 형태로 진행된다. 이 때 영역은 가로 혹은 세로 방향으로 나눌 수 있는데, 예를 들어 그림 1(b) 와 같이 가로로 나눌 경우 상단의 삼각형 부분을 행렬의 중앙을 기준으로 시계 방향으로 회전시켜 하단의 여백에 배치할 수 있다. 반대로 그림 1(c)와 같이 세로로 나누는 경우에는 우측의 잘린 부분을 반시계 방향으로 회전시켜서 재배치한다. 예컨대 그림 2에서는 행과 열에 배치된 항목이 짝수인 경우에 대해서 재배치를 적용한 결과를 나타내고 있으며, 위치가 이동된 전체 10개의 칸들 중에서 두 개의 재배치 된 칸에 대해 재배치 이전의 위치와 재배치가 끝난 후의 위치를 화살표로 나타내주고 있다.

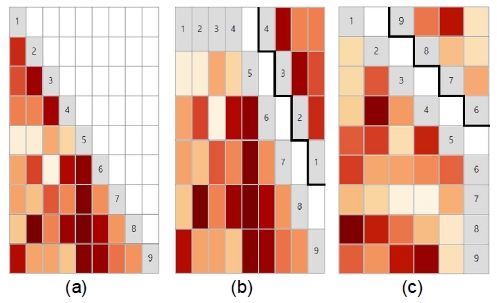
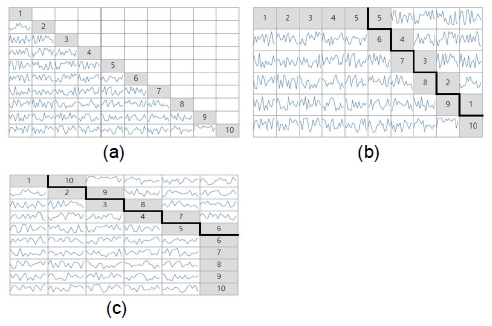
한편, 재배치를 위해서는 공간의 분할이 필요한데, 분할하는 지점은 행과 열에 배치된 항목의 수가 짝수인지 혹은 홀수 인지, 그리고 대각선 영역을 보존할 것인지 여부에 따라서 최대한으로 공간을 절약할 수 있는 위치를 찾을 수 있다. 예를 들어 그림 2와 같이 라벨이 배치된 대각선 영역을 보존하는 경우에는 행과 열에 배치된 항목의 수가 짝수(2n)이므로 최대 n개의 행 혹은 열을 잘라서 이동이 가능하다. 이는 그림 3(a)에서와 같이 행과 열의 수가 홀수(2n + 1)일 경우에도 동일하며, 다만 라벨이 표시된 대각선 영역을 이동함에 따라 별도의 보완이 없을 경우 그림 1(b) 혹은 그림 1(c)에서처럼 재배치되지 않는 영역에 대한 라벨이 사라질 수 있기 때문에 그림 2와 그림 3에서는 상단에 라벨을 표시하기 위한 공간을 남겨두었다.

Fig. 2.

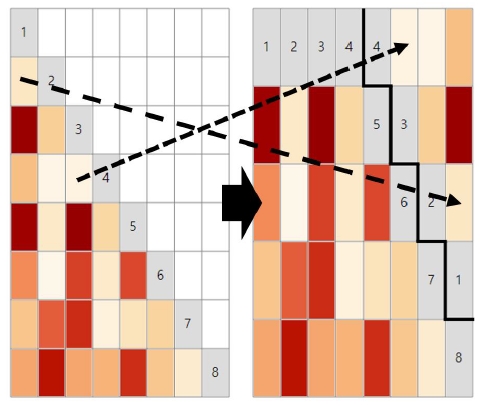
Comparison between original and rearranged layout in 9:16 screen resolution with even number of rows and columns

Fig. 3.

Comparison between (a) original and rearranged heatmaps with (b) horizontally sliced and (c) vertically sliced area in 9:16 screen resolution

3-2 화면비와 공간 재배치 방향

최근 사용되는 모니터와 스마트폰의 경우 정방형의 화면비(1:1)보다는 한쪽이 긴 장방형 화면비(16:9 혹은 9:16)를 갖는 경우가 많다. 이에 따라 제안된 기법을 적용함에 있어서 재배치 방향과 화면비율은 결과에 큰 영향을 주게 된다. 예를 들어 그림 2와 같이 세로로 긴 화면에서 가로 방향으로 영역을 나눈 후 재배치를 진행하게 되면 전체적인 공간 활용도는 높아지지만 각 칸의 화면비가 극단적으로 변하는 것을 확인할 수 있다. 이러한 경우 분할 방향을 다르게 적용하게 되면, 그림 3(c)와 같이 정방형에 가까운 영역을 확보할 수 있게 된다. 또한 가로로 긴 화면에서는 가로 방향으로 영역을 나눠서 재배치 할 경우 정방형 공간을 할당할 수 있게 된다.

이러한 영역 분할 및 재배치 방향에 따른 화면비의 조율은 각 칸별로 단일 자료를 문자나 히트맵으로 표시할 때는 큰 영향이 없을 수 있으나, 글리프나 작은 차트를 배치할 경우 공간 활용에 큰 영향을 미칠 수 있다. 예를 들어 그림 4(b)의 경우 원본과 비교했을 때 세로 방향으로의 공간을 더 확보함으로써 선 차트에서 y값의 변화를 보다 세밀하게 관찰할 수 있으며, 그림 4(c)의 경우 가로 방향으로 더 넓은 공간을 할당하여 x축을 보다 높은 해상력으로 표현할 수 있다. 또한, 선 차트에 대한 기존 연구[16]에서는 단순히 해상력의 차이에서 오는 정확도의 차이 뿐 아니라 선의 기울기에 따라 인지의 정확성에 차이가 있음을 밝힌바 있다. 따라서 분할 방향을 유기적으로 선택함으로써 각 칸의 화면비를 조율하여, 기울기의 차이를 보다 인지하기 쉽도록 차트를 그릴 수 있게 된다.

Fig. 4.

Comparison between (a) original and rearranged line charts with (b) horizontally sliced and (c) vertically sliced area in 16:9 screen resolution

4-1 정량적 공간 활용 분석

본 논문에서 제시하는 시각화 방법의 효율성을 평가하기 위하여, 기존 시각화 방법과의 공간 활용도에서의 차이를 비교해보았다. 이를 위해 기존 시각화 방법과 개선안 모두 그림 3과 같이 라벨을 표시한다고 했을 때를 기준으로 하였으며, 행과 열에 n개의 항목이 있을 때 전체 공간 대비 유의미한 내용이 존재하는 공간의 비율 R을 구해보았다. 기존 시각화의 활용 비율은 아래의 수식 (1)과 같이 도출할 수 있다.

다음으로 개선안의 경우 n이 짝수일 경우와 홀수일 경우를 나눠서 수식 (2)와 같이 도출하였는데, 짝수인 경우 그림 2와 같이 전체 영역을 모두 활용했음을 확인할 수 있다.

위의 수식에서 확인할 수 있듯, 기존 시각화의 경우 n이 커질수록 화면 내의 공간 활용 비율은 50%에, 개선안의 경우 100%에 수렴하게 된다. 또한 활용 비율뿐 아니라 각 칸에 할당되는 공간의 넓이를 비교하더라도 기존 시각화 방법은 전체 화면의 1/n² 을 할당받지만, 재배치를 하게 될 경우 그림 3(b) 와 같이 라벨을 위한 공간을 추가로 배치하더라도 전차 화면 크기의 1/n(n-1) 에 해당하는 약간 더 넓은 공간이 할당됨을 확인할 수 있다.

4-2 기존 연구와의 정성적 비교

본 시각화 기법의 평가를 위하여 관련 연구로 제시된 공간을 절약하기 위한 시각화들과의 정성적 비교를 진행하였다. 하지만 관련 연구들 중에서 TreeJuxtaposer[9], Line Graph Explorer[10], Saito et al.[11], horizon graph[12]의 경우는 나타내고자 하는 데이터가 계층적 자료이거나 시계열 자료였기 때문에 직접적인 비교가 불가능 했다. 그리고 본 연구에서 하나의 표 형태의 시각화를 상정하는 것과는 달리 NodeTrix[13]와 TileMatrix[14]는 다수의 표로 구성된 시각화를 다뤘기에 역시 비교 분석이 어려웠다. 이에 본 연구에서처럼 하나의 표로 구성된 시각화를 제시한 LiveRAC[8]과의 비교를 진행하였는데, 표 형태의 시각화를 나타내고 있지만 ROI 외의 다른 부분의 크기를 축소, 왜곡시키는 방식을 사용하고 있다는 점에서 본 연구에 비해 스몰 멀티플의 장점인 여러 시각화들 간의 직관적 비교가 힘들다는 단점을 확인할 수 있었다.

4-3 대각선 공간의 활용

본 연구에서 대각선을 따라 배치된 칸들은 각 행과 열에 대응하는 라벨을 표시하기 위하여 사용되었다. 하지만 표의 외부에 별도로 라벨을 배치하는 경우, 기존의 연구들에서는 대각선에 있는 칸들을 비워두거나, 필요에 따라 각 행 또는 열에 대해서 통계적 대푯값을 표시하였고, 행이나 열별로 전체적인 개관을 살펴보고 싶은 경우 행 또는 열별로 집계된 자료에 대한 시각화를 배치했다. 그러나 이러한 경우에도 라벨을 표시하는데 사용되는 영역이 고정적으로 할당되기 때문에, 시각화가 표시되는 영역의 공간 사용 효율성은 제고할 수 있다.

한편, 대각선 영역이 비어있었거나 아무런 의미가 없는 경우라도 대각선 영역까지 조밀하게 자료를 채우는 것은 시각적 혼잡도를 급격하게 높일 수 있다. 예를 들어 그림3(c)에서 기존처럼 6번 항목부터 9번 항목까지를 분할하지 않고, 대각선 영역까지 남김없이 사용하기 위하여 5번 항목부터 끝까지를 분할하여 배치하는 경우, 외부에 라벨이 존재하더라도 같은 열에 두 가지의 값이 대응하게 되어 인지 과정에서 혼선을 유발할 수 있게 된다. 따라서 대각선에 있었던 공간들은 조밀한 배치 과정에서도 보존이 필요하다.

4-4 재배치에 따른 인지 과정에서의 복잡도 증가

본 연구에서 제안하는 시각화 방법은 기존에 행과 열의 정렬 순서에 따라 배치되어 있던 영역의 일부분을 새로운 공간으로 이동하게 된다. 이 과정에서 평행이동이 아닌 표의 가운데를 중심으로 한 회전이동을 적용하게 되기 때문에 축의 역전 현상이 발생한다. 이에 따라 다음의 두 가지의 시각적 분석 과정에서 복잡도가 증가하게 되는데, 첫 번째는 하나의 행이나 열을 따라서 경향성을 분석하는 경우로, 전체 행이나 열 중 절반에 대해서 일부분이 분할되어 배치되기 때문에 분석이 까다로워진다. 또 한 가지 경우는 행과 열의 배치가 시각적 분석에 영향을 주는 경우로, 예를 들어 인접 행렬에서 서로 완전히 연결된 노드들을 찾고자 할 때 해당 군집 중 일부가 바로 보이지 않는 경우가 생길 수 있다. 따라서 본 배치 기법은 행과 열 단위로 분석이 이뤄지지 않으며, 행과 열의 순서를 바꿔가면서 인접한 항목들에 대한 경향성을 파악해야하는 상황이 아닐 때 가장 높은 효율성을 보일 것으로 기대된다.